空間翻滾目標位姿耦合建模與運動特性分析

郝宇星，申 麟，李 揚

（中國運載火箭技術研究院研究發展中心，北京，100076）

0 引 言

空間失效航天器與太空碎片對正常運行的航天器而言是極大的威脅，發生碰撞會產生嚴重的后果。與傳統的航天器的交會對接與編隊飛行不同的是，這一類目標航天器不能提供自身的姿軌信息，其行為難以預測，可能會有翻滾等復雜運動狀態，使得空間操作的安全性受到威脅。

翻滾是空間目標姿態運動的一種形式。在軌目標處于翻滾狀態時，可以看做一個繞質心作定點運動的剛體。這種運動與翻滾目標的自身性質（如質量、慣量分布）以及初始狀態有關。為了掌握目標器的運動狀態，便于任務設計，需要對不同條件下的翻滾目標的運動規律進行研究。

在傳統建模方法解決位姿耦合問題遇到瓶頸后，學者們嘗試用新的數學工具進行姿態和軌道的統一建模。Brodsky等[1]基于 Pennock等[2]和 Adams[3]對旋量理論的研究，首先討論了對偶慣性算子的本質和物理特性，然后使用對偶慣性算子和矢量變換規則得到對偶動量、對偶角動量、對偶力的一般表示形式，并基于這些定義推導以三維對偶形式表示的剛體動力學的牛頓-歐拉方程，為航天器一般性空間運動的研究和分析提供了理論基礎。

在進一步的理論研究上，Wang等[4，5]推導了用單位對偶四元數表示的剛體轉動和平動的動力學模型，指出單位對偶四元數是單位四元數的自然擴展，能同時表示旋轉和平移，相對于齊次變換矩陣要用 16 個數來表示空間的一般運動，而對偶四元數僅僅需8 個數，另外，在計算效率上對偶四元數也高于齊次變換矩陣。在應用研究上，Wu等[6]使用對偶四元數來設計捷聯慣性導航算法，并指出對偶四元數是同時表示剛體轉動和平動最簡潔和最有效的數學工具；Wang等[7]基于對偶四元數分別推導了交會對接最終段和兩個航天器編隊飛行的六自由度相對運動模型；Zhang等[8]推導了基于對偶四元數的剛體航天器平動和轉動組合的跟蹤誤差模型。

使用對偶數和旋量可將剛體運動的平動部分與轉動部分結合于一個框架之下，本文使用簡明的模型，使用經典力學公式推導，得到由對偶數表示的牛頓-歐拉方程，該方程形式上與歐拉方程具有相似性，并且可以直觀地看到姿軌耦合項的影響。

在對空間翻滾目標進行在軌任務前，需要對其運動狀態進行分析。對于非合作目標而言，在無法獲得其準確本體參數的條件下，需要根據其運動數據對其參數進行識別與估計，因此對翻滾目標的典型運動形式及其條件的分類格外重要。首先，本文將對翻滾目標進行分類，對不同類別目標的基本性質進行劃分；在此基礎上，應用位姿耦合動力學方程建立模型，分析在軌翻滾剛體的運動特點；最后給出 3種典型的姿態運動方式，并使用仿真舉例說明其條件。

1 空間翻滾目標的分類及特征

根據任務對象的不同，可將空間翻滾目標分為：正常工作的航天器、功能受損（需要維修）的航天器、空間碎片或廢棄部件與小行星等空間自然物體。由于針對這4類目標的任務各不相同，而且要考慮到各類目標的特性差異，翻滾帶來的姿軌耦合程度也有所不同，在面對空間翻滾目標問題時，要對其特點進行分類，內容可以分為翻滾原因、翻滾速率、慣量陣特征、質量、耦合性以及主要任務目的。表 1為空間翻滾目標特征分類。

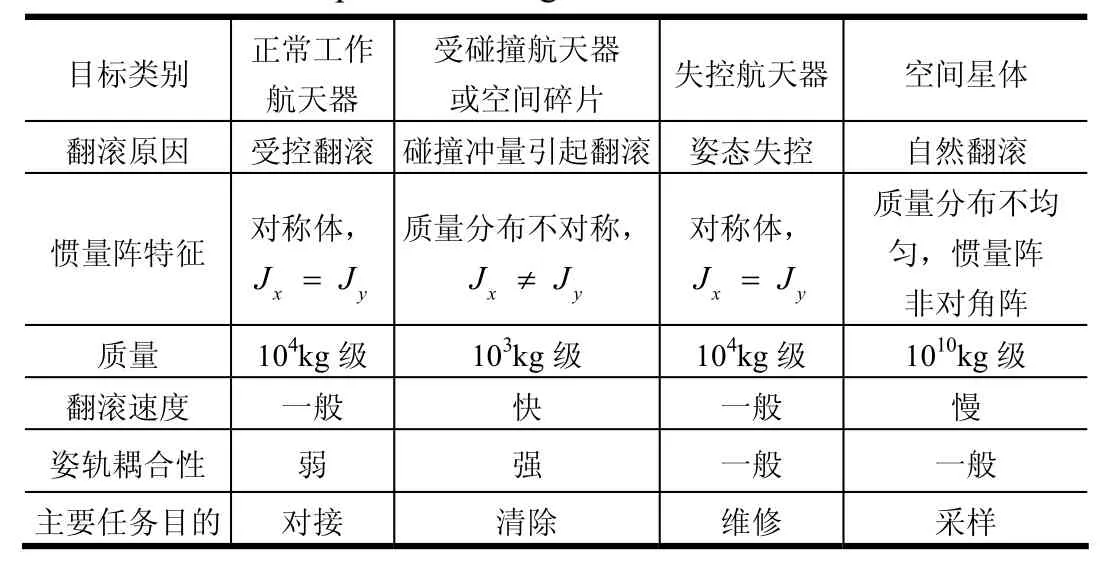
表1 空間翻滾目標特征分類Tab.1 Space Roll Target Feature Classification

2 空間目標位姿耦合動力學模型

本文采用對偶數與旋量的概念進行剛體的動力學方程推導，基于傳統的理論力學原理，與新概念相結合，得到的結果表達形式簡潔，物理意義明確，易于進行姿軌耦合分析以及一體化的任務設計。

剛體在三維空間的運動均可以表示為繞一軸線的旋轉與沿該軸的平移，因此可將六維空間的向量稱為一個旋量，映射一個三維剛體運動。幾何上用六維列向量表示，代數上可用對偶數表示，形式如下：

式中 α，α′分別為主部和副部，或稱為實部和對偶部，在表示物理量時，主部表示平移相關的量，副部表示旋轉相關的量；ε為對偶單位，其性質為

設質量為m，質心為C的衛星在軌道上運行，并帶有翻滾，如圖1所示。建立衛星的本體坐標系bS，原點位于C點，X，Y，Z軸分別為衛星的3個慣量主軸。慣性系oS的原點為O。

圖1 航天器動力學模型示意Fig.1 Spacecraft Dynamics Model

將衛星視作剛體，則在時刻t，bS的運動狀態由剛體的角速度矢量ω、C點t時刻的線速度矢量CV表示。

由于速度V與參考點有關，角速度ω與參考點無關， V與ω可構成以C為參考點的速度旋量，記為

由純力F以及與該力作用線平行的力偶T組成的力，稱為作用在旋量軸線上的力的旋量，簡稱力旋量。用對偶數表示，則為對偶力，記為

對于航天器而言，作用在其上的力分為控制力uF、地球引力 Fg、擾動力 Fd，力矩可分為控制力矩 Tu、重力梯度力矩 Tg和擾動力矩 Td。將這些力和力矩用對偶力概念統一起來，則作用在追蹤器上的合外對偶力為

定義對偶慣性算子，由對偶質量算子與對偶慣量算子組成，記為

式（10）即為對偶力與對偶動量的關系式。根據矢量積運算規則改寫為矩陣方程式，得到：

3 空間翻滾目標運動特性分析

將式（11）展開為實數部分與對偶部分：

得到：

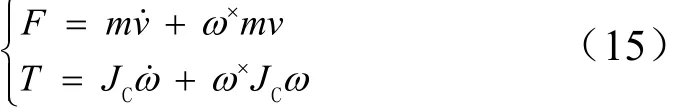
上述兩組方程是相互耦合的，當以傳統的方法研究航天器姿態運動時，通常把姿態運動對軌道運動的影響略去不計，且在分析姿態運動參數時，把軌道運動參數當作已知量，做這樣的簡化假設后，姿態運動方程便可單獨進行積分計算。進行解耦后的姿態運動方程即歐拉方程，由式（15）可以看出它是對偶動力學方程的一部分，并在以下情況的翻滾目標其運動位姿耦合最為顯著：

a）目標飛行器與追蹤器的距離較近（幾十米到幾百米）時，此時平移量與旋轉量處于相近的數量級，耦合項與非耦合項幅值接近；

b）目標飛行器的質量與慣量較大時，姿態運動導致的動量與角動量較大，對應的耦合量也較大；

c）目標飛行器存在復雜的姿態變化時，角速度項多變使得耦合項多變，影響其幅值以及方向。

對于無外力矩剛體的姿態運動問題，其解析解與幾何解在理論力學中已有結論，其中的一般情形稱為歐拉-潘索情形，其角速度軌跡在兩個橢球的交線上。對于在軌自由運動的剛體而言，其受力主要為各天體的引力、引力梯度矩，其中以地球的引力與引力梯度矩為主，其余項可當作環境干擾力與力矩處理。由于引力梯度矩的值很小，并且工程上的航天器其質心與重心可近似重合，因此在短時間內可忽略；但在長期的軌道運行條件下，其對姿態積累的影響會十分顯著。

針對在軌翻滾剛體的運動特點，以在軌翻滾航天器為例，通過設定不同的慣量矩陣、初始姿態、角速度的狀態，根據剛體定點運動規律，進行舉例分析：

假設某航天器軌道高度430 km，質量74 783 kg，處于圓軌道上做姿態運動，現使用對偶動力學模型，以航天器本體系作為計算坐標系，對各類轉動情形進行數值仿真。

a）在軌定軸轉動。

Jx= Jy= Jz時，過原點的任意軸都具有定向性；

Jx= Jy≠ Jz時，Z軸與Oxy平面的過原點的任意軸都具有定向性；

圖2 在軌定軸轉動時航天器角速度變化Fig.2 Spacecraft Palstance in Fixed-axis Rotation

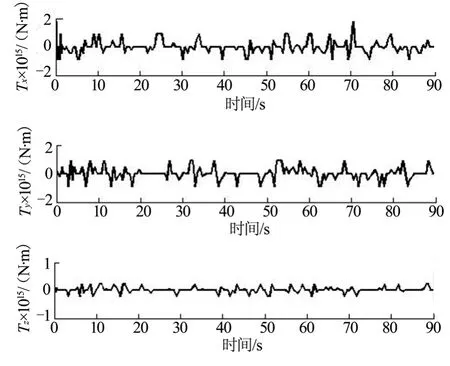
圖3 在軌定軸轉動時重力梯度矩變化Fig.3 Gravity Gradient Torque in Fixed-axis Rotation

當滿足定軸轉動條件時，航天器轉軸方向在慣性空間保持不變，且當轉軸為Z軸時，旋轉剛體受擾動后仍能保持在原來的方向近旁運動，或漸趨于原來的方向。正常工作的航天器往往處于定軸轉動狀態。由于慣量矩陣的3個分量相同，航天器受到的重力梯度力矩為零，因此航天器角速度基本不變，作定軸轉動。

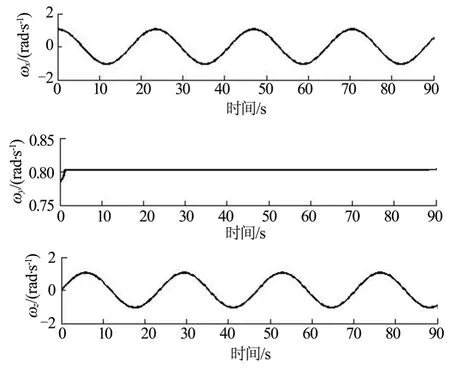
圖4 在軌規則進動時航天器角速度變化Fig.4 Spacecraft Palstance in Regular Precession

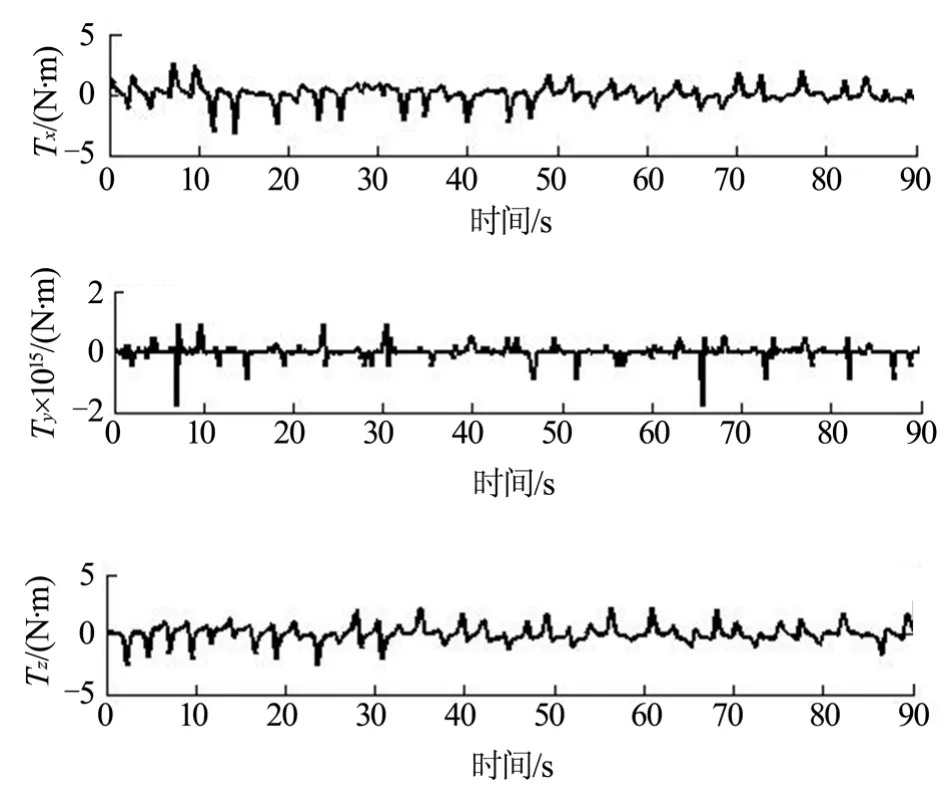
圖5 在軌規則進動時重力梯度矩變化Fig.5 Gravity Gradient Torque in Regular Precession

可以看出：當航天器角速度發生異常，但結構完好的情況下，航天器可能會規則進動。而這種角速度異常會由姿控系統故障引起。本例中航天器進動周期為 20 s，角速度矢量軌跡在本體系上為一個圓形，重力梯度矩在 ,XY軸上在零附近波動，而Z軸上進行周期變化。

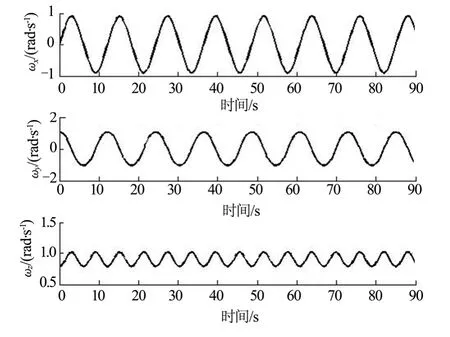
圖6 歐拉-潘索運動時航天器角速度變化Fig.6 Spacecraft Palstance in Euler-poinsot Motion

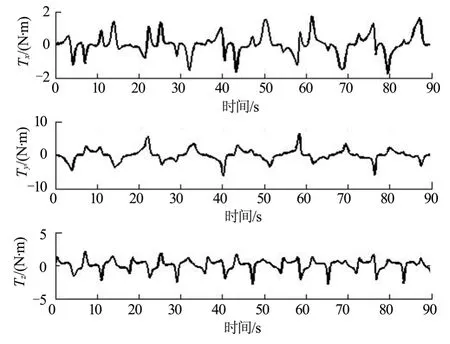
圖7 歐拉-潘索運動時重力梯度矩變化Fig.7 Gravity Gradient Torque in Euler-poinsot Motion

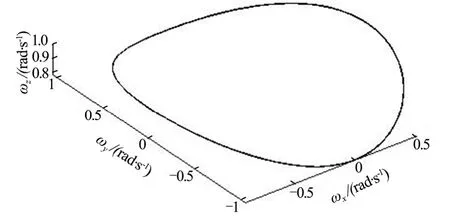
圖8 歐拉-潘索運動時角速度矢徑變化Fig.8 Palstance Vector in Euler-poinsot Motion

對于不規則物體與隨即狀態而言，歐拉-潘索狀態為最為普遍的運動狀態。空間翻滾目標有大量的空間碎片以及小行星體，其質量與形狀很不規則，姿態運動由碰撞產生，有很強的隨機性，因此這類目標通常作歐拉-潘索運動。由結果可以看出，受到重力梯度矩的影響后航天器的Z方向角速度成周期變化，結合進動效果后角速度的軌跡在本體系中表現為馬鞍面邊際線（兩橢球的交線）。

4 結 論

空間翻滾目標在軌道上雖然受到引力與環境干擾力的影響，但其姿態運動方式依然可以按照無外力矩剛體定點運動規律劃分，并且根據其運動特征可以反推其質量特性，這對空間目標運動的識別與參數估計擁有重要參考意義。本文使用對偶數作為運動參數的表達形式，其輸入輸出均為6維，對于空間目標運動的初步識別與耦合估計非常實用，但為了得到更加精確的結果，仿真需要較高的運算精度，否則誤差項的耦合放大會對結果產生很大影響，因此在解決高精度位姿估計問題時，需要對該仿真系統進行更深入的理論研究。