基于有限元法的不同帶槽球面軸承結構的對比分析*

(1.河北科技大學電氣工程學院 河北石家莊 050018；2.安徽大學高節能電機及控制技術國家地方聯合工程實驗室 安徽合肥 230601)

帶槽球面軸承是一種有球缺的外球殼內表面設有螺旋形或環形凹槽的特殊球面軸承，相比普通的球面軸承，凹槽的結構設計改善了軸承的潤滑環境、散熱能力和力學性能。另外，可在凹槽上安裝滾珠，將滑動摩擦變為滾動摩擦，實現摩擦類型的轉變。帶槽球面軸承主要應用于永磁多自由度運動電機，如圖1所示，電機主要由電磁結構和球面軸承結構組成，通過電磁結構，利用混合驅動模式，實現電機高精度多自由度運動。球面軸承為電機的流固結構，其完整球面的內球殼作為永磁多自由度球面電機的轉子殼，有球缺的外球殼作為電機的定子殼，轉子殼做多自由度運動，定子殼保持靜止，定轉子球面密封一層潤滑油，液質潤滑油將發生相對運動的定轉子球面分隔開來，由潤滑油承受載荷，使電機運轉平穩，摩擦磨損較小，從而提高電機的效率和壽命，使永磁多自由度電機朝著更加高效環保、高精度定位方向發展，為航空航天、機器人仿生、船舶系統等需要多自由度運動設備的領域帶來了廣泛的發展前景[1-5]。

目前，專家和學者對不同帶槽軸承開展了一系列研究工作，取得了重要的研究成果[6-11]。律輝等人[11-13]針對不同螺旋角、螺旋槽數目和螺旋槽半徑大小的艉軸承模型，應用 Ansys軟件對其進行結構靜力分析對比，得到了適中的艉軸承結構；同時通過靜態接觸仿真分析，得到不同螺旋槽數和不同螺旋角度艉軸承，在不同載荷和不同橡膠硬度等條件下的接觸狀況。王建等人[14]研究了3種不同型腔結構以及不同腔深的長方形腔艉軸承的靜力學性能，為改善艉軸承的承載能力和工作環境提供了指導。李振宇等[15]通過對不同導水槽結構軸承的仿真與對比分析，發現導水槽尺寸及導水槽所在位置處壓強對軸承承載能力有重要的的影響。

目前對球面軸承進行凹槽結構設計及性能研究仍然較為欠缺，本文作用利用有限元仿真軟件，對比分析不同螺旋槽和環形槽結構對球面軸承的位移、應力和體積應變分布等力學性能的影響，然后對比2種槽結構，選取最合適的結構和尺寸，為優化球面軸承的結構設計和提高其潤滑性能等提供理論參考。

1 帶槽球面軸承模型

1.1 三維實體模型的建立

球面軸承由2部分組成：非完整球面的外球殼和完整球面的內球殼，內球殼裝于外球殼內。帶槽球面軸承的槽結構主要有螺旋槽和環形槽，如圖2所示。利用 Solidworks 繪圖軟件繪制不同槽數目和槽半徑的2種槽類型球面軸承外球殼的三維實體模型[16]，槽半徑分別為2、2.5、3 mm，槽數目為3、5、7。對于螺旋槽球面軸承，螺旋角不同，螺旋槽的數目也不同，螺旋角為5°、10°、15°時，槽數分別為3、5、7，如圖3所示。將螺旋槽和環形槽球面軸承導入多物理場分析軟件，對不同槽球面軸承模型進行對比研究。

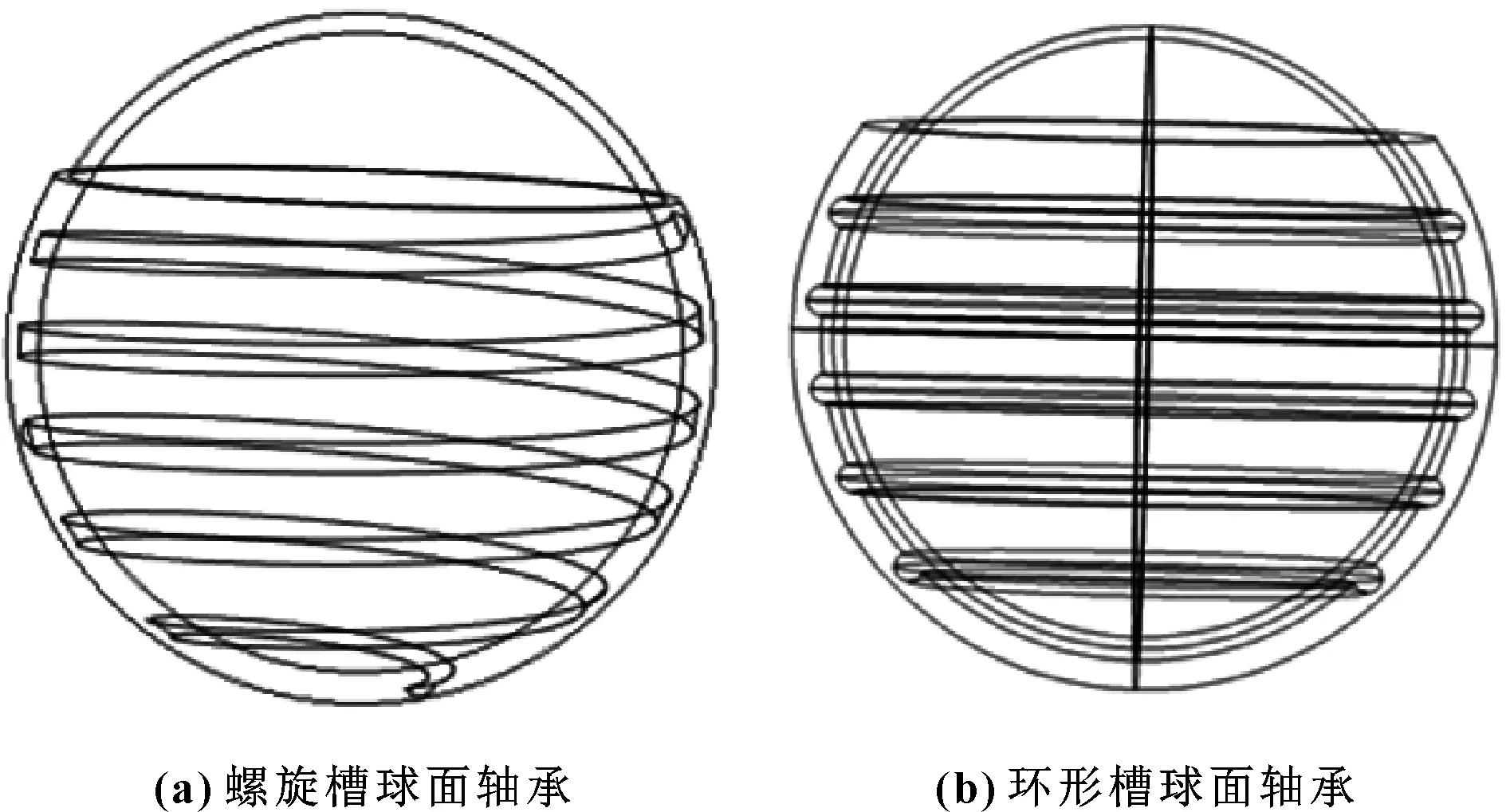
圖2 球面軸承模型示意圖Fig 2 Schematic diagram of spherical bearing model(a)spiral groove spherical bearing;(b)annular groove spherical bearing

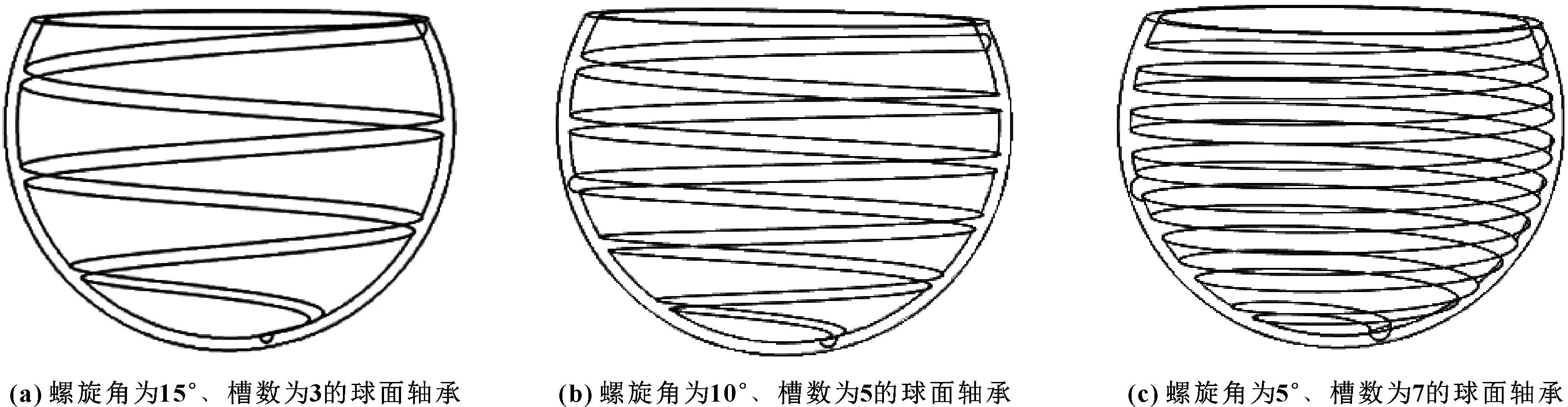
圖3 不同螺旋角的球面軸承模型示意圖Fig 3 Schematic diagram of spherical bearing model with different helix angle(a)spherical bearing with a helix angle of 15° and a groove number of 3;(b)spherical bearing with a helix angle of 10° and a groove number of 5;(c)spherical bearing with a helix angle of 5° and a groove number of 7

1.2 模型參數選擇和邊界條件

球面軸承的內外球殼的材料為結構鋼，其彈性模量為2×105MPa，泊松比為0.3，熱膨脹系數為1.23×10-5℃-1，密度為7 850 kg/m3，具體模型參數如表1所示。

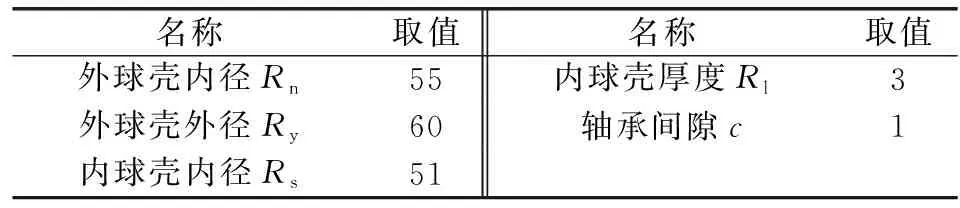
表1 球面軸承模型基本參數Table 1 Basic parameters of the spherical bearing model mm

假設球面軸承在理想狀態下對其進行分析，簡化條件[5]為

(1)內外殼間的液體油膜為牛頓流體；

(2)不計油膜的質量，不存在慣性力和重力；

(3)軸承處于動壓潤滑狀態，在穩態下工作；

(4)液體油膜與內外殼接觸的邊界上沒有相對滑動。

2 模型分析方法

(1)建立幾何模型。以螺旋角為10°，槽數為5，半徑為2.5 mm的螺旋槽球面軸承外球殼為例，應用Solidworks軟件繪制[16]將其導入到COMSOL Multiphysics軟件進行仿真分析。

(2)添加材料和全局定義。在內置材料庫中添加Structural steel[16]，進行材料屬性定義，在全局定義下添加參數，定義外殼內表面上承受的載荷數。

(3)添加物理場和邊界條件。在“結構力學”模塊下添加“固體力學”物理場，球面軸承內表面為受壓區域，凹槽上的載荷相對大一些，不僅有油膜的載荷還有滾珠的載荷，為主要的載荷承載區。文中主要分析凹槽處的力學性能。軸承滿足動壓潤滑壓力分布，將其分割成不同的區域，每個區域的壓力進行

離散分布，另外對球面軸承的外表面施加固定約束，確保它不會發生移動。

(4)添加網格。劃分網格是有限元分析的至關重要的一步，網格質量、數目及疏密等對計算結果的精度和收斂性有著重要的影響。在凹槽區域網格進行細化，以便提高運算精度，得到如圖4所示的結果。

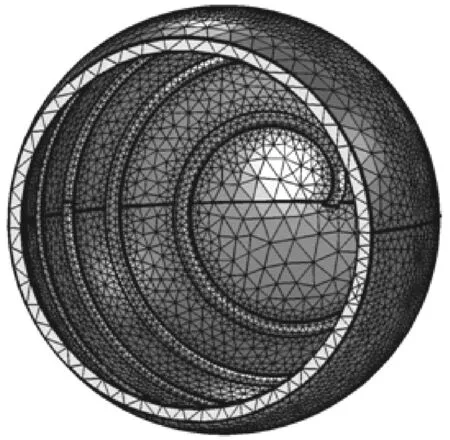
圖4 球面軸承網格劃分圖Fig 4 Spherical bearing meshing diagram

3 結果及分析

3.1 槽數對球面軸承力學性能的影響

設球面軸承的螺旋槽和環形槽半徑均為2.5 mm，槽數分別為3、5、7，其他基本尺寸參數和所承受的載荷均相同。對6種球面軸承模型的位移進行分析，結果分別如圖5和圖6所示。

由圖5可知：不同螺旋槽數的3種球面軸承模型的位移分布位置沒有明顯差異，都發生了微小的位移；位移集中現象多出現在外球殼的上邊緣部位，變化幅度都比較平緩；其中可明顯看出螺旋槽數為5的球面軸承的位移量最小。

圖6所示為3種不同環形槽數球面軸承位移分布情況，可以看出：環形槽球面軸承的位移分布位置發生了顯著的變化，形變處分布在環形槽上，定子殼底端的環形槽位移量最大；隨著環形槽數的增多，球面軸承的位移量增大，環形槽數為7的球面軸承位移量最大。

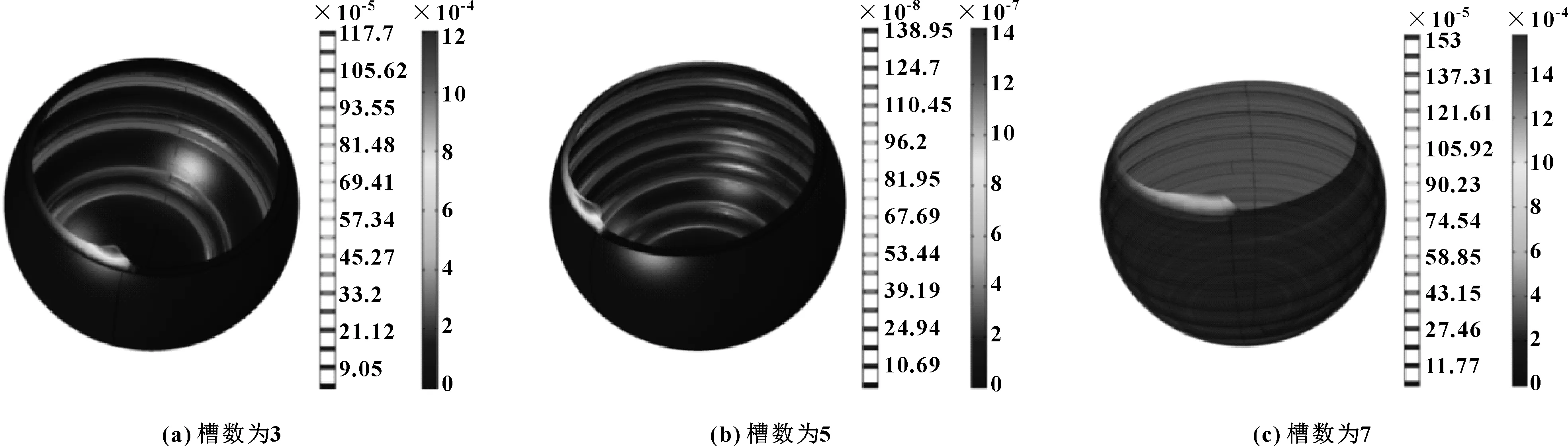
圖5 不同螺旋槽數的球面軸承位移分布圖(m)Fig 5 Displacement distribution diagram of spherical bearings with three different spiral groove numbers(m)(a) with a groove number of 3;(b)with a groove number of 5;(c)with a groove number of 7

圖6 不同環形槽數的球面軸承位移分布圖(m)Fig 6 Displacement distribution diagram of spherical bearings with three different annular groove numbers(m)(a) with a groove number of 3;(b)with a groove number of 5;(c)with a groove number of 7

通過比較圖5和圖6可知：由于凹槽結構不同，發生位移的位置明顯不同，環形槽球面軸承發生形變的位置影響著潤滑油膜的流動狀態，因此螺旋槽球軸承比較滿足實際工況。

如圖7所示，不同螺旋槽數的3種球面軸承的應力分布趨勢相似；螺旋槽數為3的球面軸承應力分布不均勻，多次出現了紅色的應力值高峰區域，容易形成應力集中現象；螺旋槽數為5的球面軸承的應力分布相對均勻；螺旋槽數為7的球面軸承的應力分布較為平緩；隨著螺旋槽數的增多球面軸承的應力也逐漸增大。

圖7 不同螺旋槽數的球面軸承應力分布圖(Pa)Fig 7 Stress distribution of spherical bearings with three different spiral groove numbers (Pa)(a) with a groove number of 3;(b)with a groove number of 5;(c)with a groove number of 7

如圖8所示，不同環形槽數的球面軸承應力分布情況大體一致，環形槽數的改變對球面軸承的應力值沒有顯著影響，但加劇了球面軸承的應力集中現象；環形槽數為7的球面軸承出現紅色的應力值高峰區域比較集中；相比3 種模型，螺旋數為5的球面軸承較為優越。

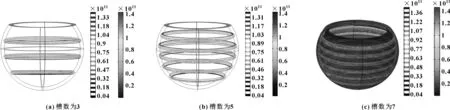
圖8 不同環形槽數的球面軸承應力分布圖(Pa)Fig 8 Stress distribution diagram of spherical bearings with three different annular groove numbers(Pa)(a) with a groove number of 3; (b)with a groove number of 5;(c)with a groove number of 7

如圖9、10所示，3種不同螺旋槽數和環形槽數的球面軸承體積應變分布趨勢與應力分布趨勢大體一致，應變值高峰也都出現在外球殼上邊緣，與位移和應力分布情況相似。環形槽球面軸承的體積應變量隨著槽數的增多變化不大，環形槽數為3和5的球面軸承體積應變量相同，環形槽數為7的球面軸承的體積應變分布明顯出現不均勻現象。

圖9 不同螺旋槽數的球面軸承體積應變分布圖Fig 9 Volumetric strain distribution diagram of spherical bearings with three different spiral groove numbers(a) with a groove number of 3; (b)with a groove number of 5;(c)with a groove number of 7

圖10 不同環形槽數的球面軸承體積應變分布圖Fig 10 Volumetric strain distribution diagram of spherical bearings with three different annular groove numbers(a) with a groove number of 3;(b)with a groove number of 5;(c)with a groove number of 7

為了清晰直觀地反映不同槽數目的螺旋槽和環形槽對球面軸承力學性能的影響，計算了槽半徑相同、槽數目不同的6種螺旋槽和環形槽球面軸承的最大位移、最大應力和最大應變量，如表2所示。對比分析得知：螺旋槽數為5的球面軸承的位移量最小，其值為138.95×10-8m，其他5種的球面軸承的最大位移量大致相同；隨著槽數的增多，螺旋槽球面軸承的最大應力和最大體積應變值都增大，而環形槽的最大應力值和最大體積應變值變化不大，即與環形槽相比，螺旋槽的最大應力值和最大體積應變值要大一些。

表2 不同槽數的螺旋槽和環形槽球面軸承的最大位移、最大應力和最大體積應變量Table 2 The maximum displacement,maximum stress and maximum volume strain for spiral groove and annular groove ball bearings with different groove numbers

綜合以上分析結果，可以得出以下結論：槽數目和槽結構對球面軸承力學性能有著明顯的影響，6種球面軸承的應力值和體積應變值隨著槽數目和槽結構的變化而發生規律性變化；但螺旋槽數對位移量的影響較為復雜，其中螺旋槽數為3和7時，位移量都大于螺旋槽數為5的位移量，且螺旋槽數為5時，其位移分布位置相對合理；相比環形槽，螺旋槽應力應變分布相對均勻；設計球面軸承凹槽結構應該盡量避免出現應力、應變集中的現象。通過比較上述6種結構可以得出：螺旋槽數為5的球面軸承的力學性能要比其他5種結構優越。

3.2 槽半徑對球面軸承力學性能的影響

由以上分析比較，優選出了螺旋槽數目為5的球面軸承結構，現以槽數目為5為例，建立不同螺旋槽和環形槽半徑的6種球面軸承，螺旋槽和環形槽半徑分別為2、2.5、3 mm，其他結構尺寸參數都相同。對6種球面軸承進行有限元靜力分析，得到位移、應力、體積應變分布圖。

圖11、12所示分別為螺旋槽和環形槽半徑為2 mm和3 mm的球面軸承位移分布圖，不同螺旋槽和環形槽半徑的球面軸承位移分布情況大體一致，出現最大位移的部位也分別是在外球殼上邊緣和環形凹槽處，只是位移量有差異。與圖5(b)、6(b)比較可知，半徑為2.5 mm的螺旋槽位移量最小。

圖11 不同螺旋槽半徑的球面軸承位移分布圖(m)Fig 11 Displacement diagram of spherical bearings with different spiral groove radius (m)(a)R=2 mm;(b)R=3 mm

圖12 不同環形槽半徑的球面軸承位移分布圖(m)Fig 12 Displacement distribution diagram of spherical bearings with different annular groove radius(m)(a)R=2 mm;(b)R=3 mm

圖13、14所示分別為螺旋槽和環形槽半徑為2 mm和3 mm的球面軸承應力分布。可知：螺旋槽和環形槽球面軸承的應力分布都隨著槽半徑的增大而減小，這是因為半徑越大，承載壓力的區域面積越大，應力也相對較小，而且明顯看出半徑為2 mm的螺旋槽上多處出現應力集中現象，應力分布很不均勻，容易導致軸承疲勞破壞。從圖7(b)、13(b)可看出：螺旋槽半徑為2.5 mm和3 mm的球面軸承應力分布相對均勻，半徑為3 mm的球面軸承應力集中不明顯。而從圖14可看出：環形槽半徑越大，應力集中現象越顯著。對比圖13、14可知：螺旋槽球面軸承比環形槽應力分布更均勻一些。

圖13 不同螺旋槽半徑的球面軸承應力分布圖(Pa)Fig 13 Stress distribution of spherical bearings with different spiral groove radius (Pa)(a)R=2 mm;(b)R=3 mm

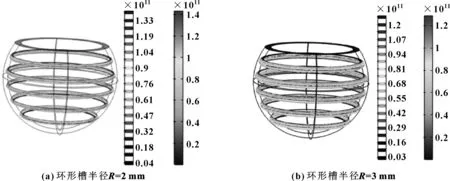
圖14 不同環形槽半徑的球面軸承應力分布圖(Pa)Fig 14 Stress distribution diagram of spherical bearings with two different annular groove radius(a)R=2 mm;(b)R=3 mm

圖15、16所示分別為螺旋槽和環形槽半徑為2 mm和3 mm的球面軸承體積應變分布。不難看出：凹槽處的體積應變值相對大一些；球面軸承體積應變隨著螺旋槽半徑的增大而增大，但環形槽半徑的增大，對軸承體積應變影響不大。

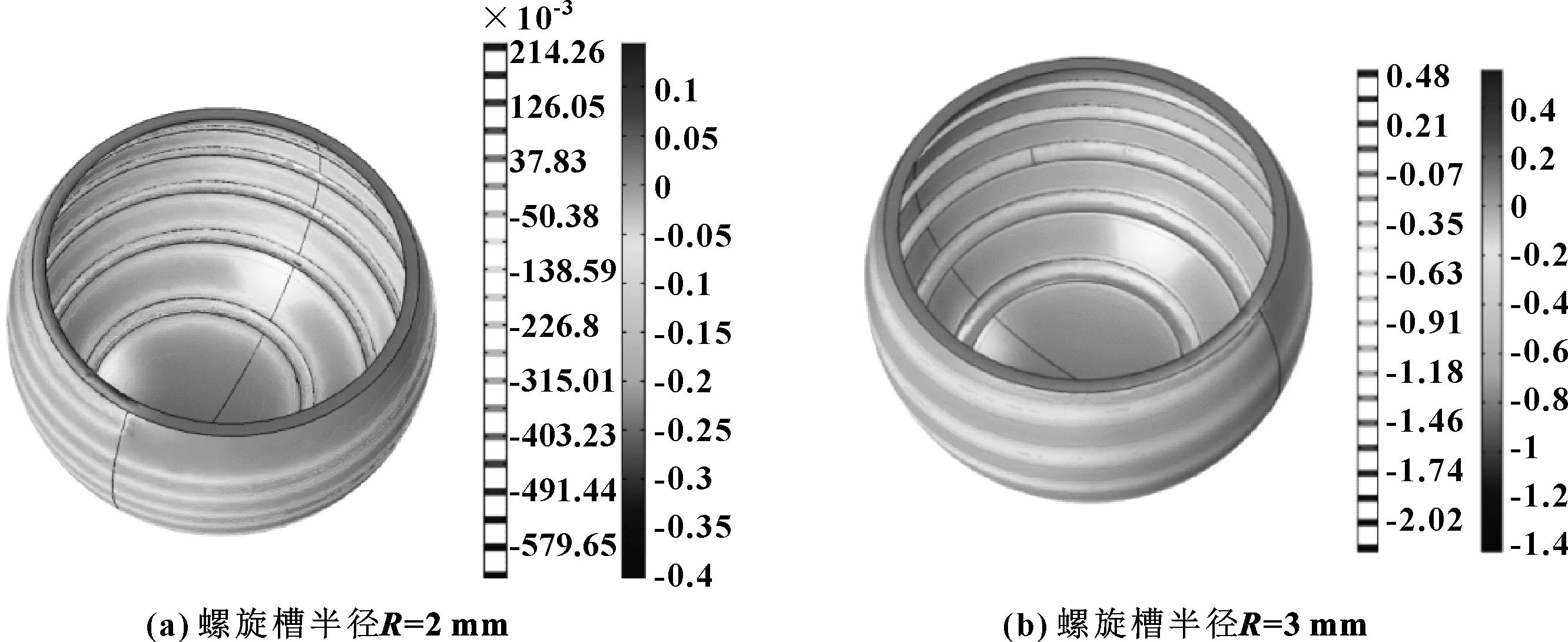
圖15 不同螺旋槽半徑的球面軸承體積應變分布圖Fig 15 Volumetric strain distribution of spherical bearings with different spiral groove radius(a)R=2 mm;(b)R=3 mm

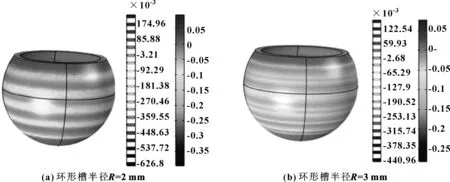
圖16 不同環形槽半徑的球面軸承體積應變分布圖Fig 16 Volumetric strain distribution diagram of spherical bearings with different annular groove radius(a)R=2 mm;(b)R=3 mm

表3所示為不同槽半徑的螺旋槽和環形槽球面軸承的最大位移、最大應力和最大體積應變量計算結果。可知：螺旋槽半徑若太小或太大都會使球面軸承的最大位移量增大，形變量也增大；環形槽的最大位移值隨著半徑增大而增大，但差值不大；螺旋槽半徑為2.5 mm的球面軸承位移峰值最小；相比環形槽，螺旋槽球面軸承的最大應力值和最大體積應變值相對大一些。

表3 不同槽半徑的螺旋槽和環形槽球面軸承的最大位移、最大應力和最大體積應變量Table 3 The maximum displacement,maximum stress and maximum volume strain of spiral groove and annular groove spherical bearings with different groove radius

綜合以上分析結果可知：環形槽球面軸承的最大位移值、最大應力值和最大體積應變值要小于螺旋槽球面軸承；環形槽與螺旋槽發生形變的部位截然不同，環形槽位移位置影響到潤滑油的流動狀態，進而影響球面軸承的承載能力，且位移變化的程度較快，形變量的面積也相對大一些；相比螺旋槽，環形槽球面軸承的應力分布不均勻，應力集中現象明顯。因此，雖然環形槽球面軸承的靜力分析最大值要小于螺旋槽球面軸承，但是從靜力分布狀況來看，螺旋數目為5，螺旋槽半徑為2.5 mm的球面軸承性能最為理想。

4 結論

(1)螺旋槽的數目和半徑對球面軸承的結構靜力分析有重要的影響，螺旋槽數和槽半徑增大或減小，球面軸承的位移都增大；隨著螺旋槽數目的增大，最大應力和體積應變值都增大；隨著螺旋槽半徑的增大，最大應力值減小，而最大體積應變值則增大。

(2)環形槽球面軸承的最大位移量隨著槽數和半徑的增大而增大；最大應力和最大體積應變量隨著環形槽數目增大及槽半徑的減小而增大。

(3)螺旋槽球面軸承的最大位移、最大應力和體積應變量大于環形槽球面軸承，但環形槽球面軸承的位移分布變化較快且范圍大，壓力分布不均勻，多次出現壓力峰值，容易造成應力集中現象。故通過對比應選取螺旋角為10°，半徑為2.5 mm的球面軸承最大位移最小，最大應力值和最大體積應變值適中，應力應變分布相對均勻。

(4)不同結構和尺寸的槽結構對球面軸承的力學性能有很大的影響，需要合理選取槽類型和槽數目及半徑大小，有利于優化軸承結構，提高工作效率。