基于改進型變步長擾動觀察法的最大功率點跟蹤策略

寧 佩，周惠媛，胡嘉昕，王波波

（廣東工業大學 信息工程學院，廣東 廣州 510006）

0 引 言

太陽能直接輻射到地球的能量豐富、分布廣泛，對環境無污染，是國際社會公認的理想新能源。光伏發電是太陽能的重要利用形式之一。由硅半導體構成的光伏電池能夠把光能轉化為電能，而光伏電池的輸出電壓和輸出電流容易受到光照強度、溫度等外界環境的影響，呈現復雜的非線性輸出特性。當光照強度、溫度變化時，存在的唯一最大功率點（Maximum Power Point，MPP）隨之變化。為了使當前工作點始終工作在最大功率點處，最大功率點跟蹤技術（Maximum Power Point Tracking，MPPT）成為光伏發電系統的一個重要環節[1]。目前，常用的最大功率跟蹤方法有電導增量法、擾動觀察法和模糊控制等。其中，擾動觀察法因效率高、實現簡單得到了廣泛應用。定步長擾動觀察法在選取步長時無法兼顧光伏發電系統的動態響應速度和穩態響應精度[2]；而變步長擾動觀察法在光照劇烈變化時會發生誤判并產生劇烈的震蕩。針對上述問題，本文提出了一種基于符號變量判斷的擾動觀察法。該算法在變步長擾動觀察法的基礎上增加滯環環節，通過雙向擾動得出符號變量的值來確定擾動方向，使控制系統的跟蹤速度與跟蹤精度滿足需求，并有效抑制了在環境突變時最大功率點處的誤判問題。

1 光伏電池的數學模型及仿真

光伏電池受到光照時，光伏電池的兩端產生電勢差。根據量子理論、光伏電池的內部結構和輸出特性，得到光伏電池的等效電路，如圖1所示。

圖1 單個光伏電池的模型

光伏電池的輸出電壓電流表達式為：

式中，I為光伏電池的輸出電流；I0為二極管反向飽和電流；Iph為光照激發電流；Rs為光伏電池的等效串聯電阻；Rsh為光伏電池的等效并聯電阻；k為玻爾茲曼常數；A為PN結的理想因子；q為單位電子電荷量；T為外界環境溫度。設光伏電池的開路電壓為為Uoc、短路電流為Isc、最大功率點電壓為Um、最大功率點電流為Im

[3-4]。一般而言，并聯電阻Rsh很大，串聯電阻Rs很小，故式（1）可以簡化為：

在標準條件下（光照強度Sref=1 000 W/m2、溫度Tref=25 ℃），假定光照激發電流Iph=Isc，光伏電池的輸出特性可表示為：

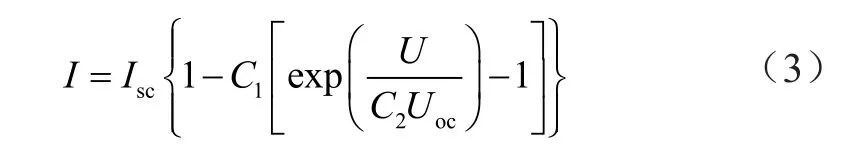
根據開路條件和系統位于最大功率點的相關約束，可得：

實際情況和標準條件下，輻射強度差ΔS和環境溫度差ΔT分別為：

為明確外界環境對輸出特性曲線的影響，在Matlab/Simulink中建立以光照強度和溫度為因變量的光伏電池數學模型。系統仿真參數設置如下：Uoc=21.5 V，Isc=0.65 A，Um=18 V，Im=0.56 A。在環境溫度為25 ℃、光照強度為1 000 S/m2時，光伏電池輸出的最大功率Pm=10.08 W，如圖2所示。

由仿真可知，光伏電池的輸出特性曲線呈現非線性狀態，不管光照強度和溫度如何變化，總存在唯一的最大功率點，只有當前工作點工作在最大功率點處，光伏系統輸出效率最大，故需要采用最大功率點跟蹤技術來控制光伏電池的實時輸出最大功率。

2 基于符號變量判斷的變步長擾動觀察法

2.1 傳統擾動觀察法的局限性分析

擾動觀察法是每隔一段時間增加或減少輸出電壓并觀測輸出功率變化方向決定下一步輸出電壓是增大還是減小。傳統的擾動觀察法中，步長為固定值，動態響應精度和穩態響應精度無法同時兼顧。步長較大時，系統對外界環境變化的響應速度快，但會導致工作點在最大功率點附近振蕩；步長較小時，提高了系統的穩態響應精度，但對外界環境變化的動態響應速度變慢，降低了光伏系統的發電效率[2-7]。因此，為了改善擾動觀察法的跟蹤效果，要兼顧光伏發電系統動態響應速度和穩態下的控制精度。

圖2 光伏電池的輸出特性曲線

為解決步長選取引發的光伏系統動態響應速度和穩態響應精度之間的矛盾，可分析光伏電池當前工作電壓U和最大功率點MPP電壓Umax之間的關系。當U＜Umax時，當前工作點運行在MPP左邊，功率對電壓導數比的絕對值在接近MPP時逐漸變小；當U＞Umax時，當前工作點運行在MPP右邊， 在遠離MPP時逐漸變大[2,7]。基于此，步長的更新規則為：

式中，dP為第k次擾動后與第k-1次擾動后的功率差；dU為第k次擾動后與第k-1次擾動后的電壓差；m為比例因子，由系統特性決定；f(i)為符號變量，取1和-1。

在光照強度穩定或變化緩慢的情況下，此算法的步長更新規則能夠兼顧光伏系統的動態和穩態性能，但在光照強度突變時無法有效穩定在最大功率點處[5-8]。當光照強度突然變化時，dP值突變，使得值突變，從而在最大功率點處出現誤判并產生嚴重的振蕩現象，降低了穩態精度。基于此，本文提出了一種新型的擾動觀察法。該方法是在變步長擾動觀察法的基礎上增加滯環環節，在滯環寬度內雙向擾動，得出兩次符號變量的值確定下一步的擾動方向，不僅避免了光照強度突變時出現的誤判現象，而且滿足了動態響應速度和穩態響應精度的要求。

2.2 擾動觀察法方向的判斷

擾動方向的判斷如圖3所示。利用當前時刻與前一時刻的電流差值dI和電壓差值dV，可計算得dP，即可得dP×dV。通過判斷dP×dV的正負，可確定當前工作點的位置，即通過符號變量f(i)的值確定下一步擾動方向，從而向最大功率點逼近；若dP×dV=0，則表明在最大功率點處；若dP×dV＞0，則表明最大功率點在當前工作點右側；若dP×dV＜0，則表明最大功率點在當前工作點左側[9]。

圖3 擾動觀察法的方向判斷

2.3 基于符號變量值的擾動觀察法方向判斷

為有效降低在外部環境突變時在最大功率點附近出現誤判的情況，在變步長擾動觀察法方向判斷的基礎上增加滯環環節。滯環環節選取的方法如下：設光伏系統的當前工作點為點A，根據系統特性設置合適的滯環寬度，由點A向兩側擾動相等步長到達點B、點C，既可形成滯環環節[6]。通過A和B、B和C之間的符號變量值，判斷當前工作點位置并確認擾動情況。設光伏系統的當前時刻工作點為A，依據判定的擾動方向擾動一小段步長M至C點，之后反向擾動兩個步長至B點，如圖4所示。

圖4 雙向擾動的符號變量值

確定三種擾動方向的判定情況。

規則1：如圖4 a所示，A向B擾動，若A、B在最大功率點的左邊，此時dP×dV＞0，令符號變量f1=1；A向C擾動，若A、C在最大功率點的左邊，此時dP×dV＞0，令符號變量f2=1；此時f=f1+f2=2，應增大電壓值。

規則2：如圖4 b所示，A向B擾動，若A點功率大于B點功率，可認為A、B在最大功率點的右邊，此時dP×dV＜0，令符號變量f1=-1；A向C擾動，若A點功率大于C點功率，可認為A、B在最大功率點的左邊，此時dP×dV＞0，令符號變量f2=1；此時f=f1+f2=0，表示當前工作點在最大功率點處或者離最大功率點很近且滿足精度要求，或者表示外部光照強度變化很快，電壓值不變。如圖4 d和圖4 e所示，表示當前工作點離最大功率點很近并滿足精度要求，保持當前電壓值不變。

規則3：如圖4 c所示，A向B擾動，若A、B在最大功率點的右邊，此時dP×dV＜0，令符號變量f1=-1；A向C擾動，若A、C在最大功率點的右邊，此時dP×dV＜0，令符號變量f2=-1；此時f=f1+f2=-2，應減小電壓值。

初始時，設i為光伏系統的當前工作點，采樣當前點的電壓U(i)、電流I(i)，并計算其輸出功率P(i)，同時令符號變量f=0。根據系統特性設定滯環寬度并令步長為M，由點i向左擾動一個步長M，記為i-1，再從i-1向右擾動兩個步長，記為i+1。采樣i-1、i+1兩點處的電壓U(i-1)、U(i+1)，電流I(i-1)、I(i+1)，并計算i-1處的輸出功率P(i-1)，i+1處的輸出功率P(i+1)。然后，分別求出 dP1、dP2、dU1、dU2，通過 dP1×dU1和dP2×dU2的取值情況決定符號變量的值來判斷擾動方向。根據系統特性設定的跟蹤精度要求，若當前的工作點滿足精度條件dP1＜e或dP2＜e，可調節開關管占空比輸出當前工作點功率，然后返回開始處準備判斷下一個工作點；若當前工作點不滿足精度要求，則調節開關管占空比繼續向最大功率點方向擾動。改進算法的流程，如圖5所示。

圖5 改進算法流程圖

3 仿真結果分析

在Matlab/Simulink仿真環境下，基于buck電路建立MPPT算法的仿真模型，系統的整體仿真模型如圖6所示。本文利用該仿真模型，分別對變步長擾動觀察法和基于符號變量判斷的變步長擾動觀察法進行仿真。

設溫度為定值25 ℃，當t=0.35 s時，光照強度從1 000 S/m2突變到800 S/m2，變步長擾動觀察法的仿真波形如圖7所示。放大t=0.35 s處的波形，如圖8所示。光伏電池的輸出功率在光照突變時出現了誤判和較大的震蕩現象，穩態輸出功率為7.79 W，由誤判造成功率損耗約為0.075 W，占輸出功率的0.96%。

圖6 光伏系統仿真模型圖

圖7 變步長擾動觀察法

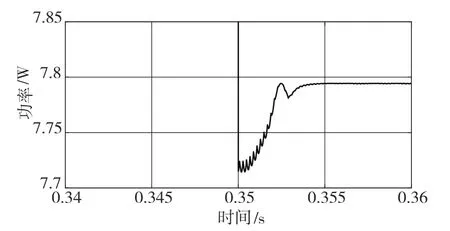
圖8 變步長擾動觀察法局部放大圖

改進算法的仿真波形如圖9所示。放大t=0.35 s處的波形，如圖10所示。光照強度突變時，輸出功率的誤判和震蕩得到有效抑制，提高了擾動方向的可靠性，幾乎沒有損耗產生，提高了光伏系統發電效率。

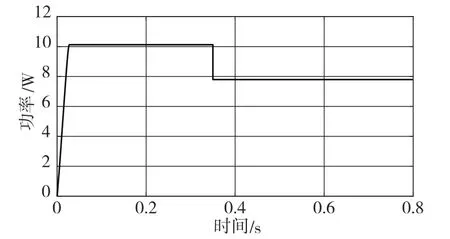
圖9 基于符號變量判斷的變步長擾動觀察法

圖10 基于符號變量判斷的變步長擾動觀察局部放大圖

4 結 論

本文對傳統的光伏MPPT算法進行改進，提出了一種增加滯環環節、基于雙向符號變量判斷的變步長擾動觀察法。在光照強度突變時，它與傳統的變步長擾動觀察法進行了仿真對比。仿真結果顯示，該算法具有良好的動態響應速度和穩態跟蹤精度，在光照強度突變時能夠有效抑制最大功率點處的震蕩現象，并避免系統誤判的發生，提高了光伏系統的發電效率，具有較高的實用價值。