一類內(nèi)共振非線性隨機(jī)振動(dòng)系統(tǒng)的可靠性控制

齊玉明， 吳勇軍

(上海交通大學(xué) 工程力學(xué)系，上海 200240)

結(jié)構(gòu)或機(jī)械系統(tǒng)常常受到隨機(jī)激勵(lì)的作用。為獲得系統(tǒng)的統(tǒng)計(jì)信息，一個(gè)簡單易行的辦法是采用數(shù)值模擬，但數(shù)值模擬需要耗費(fèi)大量計(jì)算時(shí)間。另一方法是基于合理數(shù)學(xué)模型的理論分析法。目前，最成熟的理論方法是基于擴(kuò)散的Markov過程理論[1]。為應(yīng)用該理論，隨機(jī)激勵(lì)常常需模型化為高斯白噪聲。經(jīng)添加Wong-Zakai修正項(xiàng)，系統(tǒng)的運(yùn)動(dòng)微分方程可用It隨機(jī)微分方程表示。系統(tǒng)的動(dòng)態(tài)可靠性函數(shù)、瞬態(tài)(穩(wěn)態(tài))響應(yīng)概率密度等可通過求解相應(yīng)的后向Kolmogorov方程或Fokker-Planck-Kolmogorov(FPK)方程得到。由于實(shí)際系統(tǒng)通常是多自由度系統(tǒng)，相應(yīng)地，這兩個(gè)方程常常為高維偏微分方程，數(shù)學(xué)上求解很困難，一般只能數(shù)值求解[2]。

研究中常常需要對(duì)系統(tǒng)施加反饋控制，以達(dá)到一定的設(shè)計(jì)目的。對(duì)于一個(gè)隨機(jī)系統(tǒng)，研究得最多、理論上最成熟的是擴(kuò)散Markov過程的隨機(jī)最優(yōu)控制問題，其控制的目的是使系統(tǒng)的某項(xiàng)指標(biāo)達(dá)到最優(yōu)。求解隨機(jī)最優(yōu)控制問題的兩個(gè)主要方法是Pontryagin極大值原理與Bellman的動(dòng)態(tài)規(guī)劃[3]。關(guān)于動(dòng)態(tài)規(guī)劃方法已有很多的研究成果。應(yīng)用該方法的主要困難在于求解高維非線性的Hamilton-Jacobi-Bellman(HJB)方程,大多數(shù)情況下，只能得到數(shù)值解，無法獲得精確解析解[4-5]。

可見，無論是對(duì)隨機(jī)動(dòng)力學(xué)還是隨機(jī)最優(yōu)控制問題的研究，經(jīng)常會(huì)碰到高維問題。為簡化問題的數(shù)學(xué)處理，一個(gè)有效的方法是模型降階(Model Reduction)。模型降階是一個(gè)重要的問題，在結(jié)構(gòu)動(dòng)力學(xué)、計(jì)算數(shù)學(xué)、系統(tǒng)與控制中都會(huì)碰到[6]。在隨機(jī)動(dòng)力學(xué)中，隨機(jī)平均法是一種強(qiáng)有力的降階方法。迄今，已發(fā)展了多類隨機(jī)系統(tǒng)的隨機(jī)平均法。由于具有諸多優(yōu)點(diǎn)，隨機(jī)平均法已被廣泛用于系統(tǒng)的響應(yīng)預(yù)測(cè)、可靠性估計(jì)以及穩(wěn)定性分析等[7]。自然地，將隨機(jī)平均法與動(dòng)態(tài)規(guī)劃原理結(jié)合，將為隨機(jī)最優(yōu)控制問題的研究帶來極大的便利。近20年中，朱位秋等將隨機(jī)激勵(lì)的擬哈密頓系統(tǒng)隨機(jī)平均法與動(dòng)態(tài)規(guī)劃原理結(jié)合，提出了以響應(yīng)最小、可靠度最大、穩(wěn)定度最大為目標(biāo)的多自由度擬哈密頓系統(tǒng)隨機(jī)最優(yōu)控制方法。朱位秋等通過數(shù)值模擬及工程實(shí)例，驗(yàn)證了該方法的有效性。

動(dòng)態(tài)可靠性問題是隨機(jī)動(dòng)力學(xué)中的一個(gè)重要問題，與系統(tǒng)的狀態(tài)遷移和使用壽命密切相關(guān)。為提高系統(tǒng)可靠性，需要研究反饋控制。如前所述，在可靠性最優(yōu)控制的理論分析中，將隨機(jī)平均法與動(dòng)態(tài)規(guī)劃原理結(jié)合亦是一種有效的方法。近10年，已有的研究大多采用了該方法[8-10]。朱位秋等在高斯白噪聲激勵(lì)的擬哈密頓系統(tǒng)隨機(jī)平均法的基礎(chǔ)上，結(jié)合隨機(jī)動(dòng)態(tài)規(guī)劃原理，給出了高斯白噪聲激勵(lì)下擬不可積、無內(nèi)共振擬可積、無內(nèi)共振擬部分可積三類擬哈密頓系統(tǒng)可靠性最優(yōu)控制問題的一般性數(shù)學(xué)提法。應(yīng)該指出的是，在應(yīng)用隨機(jī)平均法研究多自由度隨機(jī)振動(dòng)系統(tǒng)可靠性的最優(yōu)控制時(shí)，需要區(qū)分系統(tǒng)是否存在內(nèi)共振。已有的研究中，為簡化問題的數(shù)學(xué)處理，沒有考慮存在內(nèi)共振的情況。

本文將無內(nèi)共振情況加以推廣，研究了一類擬可積哈密頓系統(tǒng)在有內(nèi)共振情況下首次穿越可靠性的最優(yōu)控制。隨機(jī)激勵(lì)模型化為高斯白噪聲。利用廣義諧和函數(shù)隨機(jī)平均法，受控系統(tǒng)的運(yùn)動(dòng)方程簡化為部分平均的It隨機(jī)微分方程。基于動(dòng)態(tài)規(guī)劃原理，建立了以可靠度最大為目標(biāo)的動(dòng)態(tài)規(guī)劃方程，求得了最優(yōu)控制力。進(jìn)一步，得到了最優(yōu)控制系統(tǒng)的It隨機(jī)微分方程，分別建立了控制系統(tǒng)的條件可靠性函數(shù)與平均首次穿越時(shí)間滿足的后向Kolmogorov方程及Pontryagin方程，給出了邊界條件及初始條件。在具體算例中，得到了受控及未控系統(tǒng)的條件可靠性函數(shù)和平均首次穿越時(shí)間，用Monte Carlo數(shù)值模擬驗(yàn)證了理論方法的有效性。

1 內(nèi)共振系統(tǒng)的部分平均It隨機(jī)微分方程

考慮如下受弱高斯白噪聲及弱反饋控制作用的n自由度擬哈密頓系統(tǒng)：

εui(Q,P),

i,j=1,2,…，n;k=1,2,…，m

(1)

此處，Q=[Q1,Q2, …,Qn]T,P=[P1,P2, …,Pn]T,Qi、Pi分別為廣義位移和廣義動(dòng)量；H是哈密頓函數(shù)；cij(Q，P)表示阻尼系數(shù)；Zk(t)是平穩(wěn)高斯白噪聲，自相關(guān)函數(shù)為Rkl(τ)=E[Zk(t)Zl(t+τ)]=2Dkl×δ(τ)；hik(Q，P)表示隨機(jī)激勵(lì)的幅值；ui(Q，P)表示反饋控制力；ε是小參數(shù)。重復(fù)下標(biāo)表示求和。

注意到保守的哈密頓系統(tǒng)可以是可積、不可積的。假設(shè)(1)中的哈密頓函數(shù)H經(jīng)正則變換是可分離的，即

(2)

大多數(shù)情況下，H表示系統(tǒng)總能量，Hi代表各子系統(tǒng)能量，可表示為

(3)

Ui表示勢(shì)能，定義dUi/dQi=gi(Qi)。由此，系統(tǒng)(1)表示一類受控的擬可積哈密頓系統(tǒng)，可進(jìn)一步改寫為

εui(Q,P),

i,j=1,2,…n;k=1,2,…m

(4)

將系統(tǒng)(4)的解表示為如下的廣義諧和函數(shù)形式[11]：

Qi(t)=AicosΦi(t)+Bi,

Pi(t)=-Aiνi(Ai,Φi)sinΦi(t)

(5)

此處，

Φi(t)=τi(t)+Θi(t),

(6)

式中：Ai、τi、Θi、Φi、νi及Bi均為隨機(jī)過程，式(6)中，Ai、νi分別為第i個(gè)子系統(tǒng)的振幅和瞬時(shí)頻率。Bi可通過如下關(guān)系式確定[3]：

Ui(Ai+Bi)=Ui(-Ai+Bi)=Hi

(7)

平均頻率ωi(Ai)可由如下關(guān)系得到

(8)

可有如下的近似關(guān)系：

Φi(t)≈ωi(Ai)t+Θi

(9)

結(jié)合式(4)～(5)，可得如下的隨機(jī)微分方程：

i=1,2,…,n;k=1, 2,…,m

(10)

此處，

A=[A1,A2,…An]T,Φ=[Φ1,Φ2,…Φn]T,u=[u1,u2,…un]T,

(11)

方程(10)是Stratonovich意義下的隨機(jī)微分方程。添加Wong-Zakai修正項(xiàng)，得如下It隨機(jī)微分方程：

(12)

Be(t)為獨(dú)立維納過程。漂移與擴(kuò)散系數(shù)為：

i,i1,j1=1,2,…n;p=1,2;

k,s=1,2…m;e=1,2…m

(13)

考慮系統(tǒng)(4)存在內(nèi)共振的情況，此時(shí)，各子系統(tǒng)的平均頻率ωi(Ai)之間存在如下(個(gè) (1≤η≤n-1)關(guān)系：

Nsjωj=εσs,s=1,2,…,η;j=1,2,…,n

(14)

這里的Nsj為整數(shù)，σs為小參數(shù)。

引入η個(gè) (1≤η≤n-1)新變量：

Γs=NsjΦj,

s=1,2,…η;j=1,2,…n

(15)

i,j=1,2,…,n;z=η+1,…,n;

s=1,2,…,η;e=1,2,…,m

(16)

方程(16)中，Γ=[Γ1,Γ2, …,Γη]T，Φ′=[Φη+1, …,Φn]T。利用式(15)，[Φ1,…,Φη]T可用[Γ1,Γ2, …,Γη]T表示。

由(16)可以看到，隨機(jī)過程[A,Γ]T為慢變過程，而Φ′為快變過程。對(duì)快變過程做平均，得到如下平均It隨機(jī)微分方程：

i=1,2,…,n;s=1,2,…,η

(17)

平均后的漂移與擴(kuò)散系數(shù)為：

i,j=1,2,…,n;s1,s2=1,2,…,η

(18)

由于控制力u未知，方程(17)中只得到部分平均的漂移系數(shù)。

2 動(dòng)態(tài)規(guī)劃方程與最優(yōu)控制律

從式(5)可以看到，隨機(jī)過程A表示振幅，在[0,+∞)隨機(jī)變化。可認(rèn)為Ai超過某個(gè)閾值A(chǔ)ic，系統(tǒng)即發(fā)生首次穿越損壞。施加控制的目的是減小系統(tǒng)發(fā)生損壞的概率，以使系統(tǒng)的可靠性最大，或平均首次穿越時(shí)間最長。定義如下的值函數(shù)：

τp∈(t,tf]Α(t,u)∈Ωs}

(19)

Ωs為系統(tǒng)的安全域，u∈U表示控制約束，tf是控制終了時(shí)刻。式(19)表示V(t,A)是最優(yōu)控制系統(tǒng)的可靠性函數(shù)。根據(jù)Zhu的專著，V(t,A)滿足如下的動(dòng)態(tài)規(guī)劃方程：

0≤t≤tf,Ai∈[0,Aic),i,j=1,2,…,n

(20)

類似地，對(duì)平均首次穿越時(shí)間最長的控制問題，定義如下的值函數(shù)：

(21)

τp(Α,u)表示首次穿越時(shí)間，E表示數(shù)學(xué)期望。V1滿足如下的動(dòng)態(tài)規(guī)劃方程[3]：

(22)

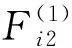
ui≤δi,i=1,2,…,n

(23)

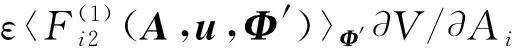
(24)

顯然，可靠性函數(shù)是振幅Ai的遞減函數(shù)[10]。因此?V/?Ai<0。注意到gi(Ai+Bi)和(1+ρi)通常都為正。(24)進(jìn)一步簡化為：

(25)

將式(25)的最優(yōu)控制力代入方程式(17)，完成平均，得到如下完全平均It隨機(jī)微分方程：

i=1,2,…,n;s=1,2,…,η

(26)

完整的漂移系數(shù)為：

(27)

3 最優(yōu)控制系統(tǒng)的條件可靠性函數(shù)與平均首次穿越時(shí)間

方程式(26)描述了最優(yōu)控制系統(tǒng)的狀態(tài)。最優(yōu)控制系統(tǒng)的條件可靠性函數(shù)Rc(t|A0,Γ0)為初始狀態(tài)[A0,Γ0]T及時(shí)間t的函數(shù)，其數(shù)學(xué)定義為：

Rc(t|Α0,Γ0)=Probability{[Α(τp),Γ(τp)]T∈Ωs,

τp∈[0,t] [Α0,Γ0]T∈Ωs}

(28)

根據(jù)擴(kuò)散過程理論，Rc(tA0,Γ0)滿足如下的后向Kolmogorov方程：

(29)

偏微分方程式(29)的邊界和初始條件為：

Rc(0A0,Γ0)=1,Ai0∈[0,Aic),Γs0∈[0,2π],

Rc(tA0,Γ0)=0,Ai0=Aic,Γs0∈[0,2π],

Rc(t0,Γ0)=finite,Γs0∈[0,2π],

Rc(tA0,0)=Rc(tA0,2π)

(30)

首次穿越時(shí)間T的概率密度通過下式求得：

(31)

最優(yōu)控制系統(tǒng)的平均首次穿越時(shí)間μc(A0,Γ0)是初始狀態(tài)[A0,Γ0]T的函數(shù)，由如下的Pontryagin方程確定：

(32)

偏微分方程(32)滿足如下的邊界條件：

μc(A0,Γ0)=0,Ai0=Aic,Γs0∈[0,2π],

μc(0,Γ0)=finite,Γs0∈[0,2π],

μc(A0,0)=μc(A0, 2π)

(33)

方程式(29)與(32)是高維偏微分方程，通常只能通過數(shù)值方法求解，如有限差分法。

4 算 例

考慮如下受高斯白噪聲及弱控制作用的二自由度Duffing-van der Pol系統(tǒng)。運(yùn)動(dòng)微分方程為：

(34)

Zij(t) (i,j=1, 2)為獨(dú)立的平穩(wěn)高斯白噪聲，強(qiáng)度為2Dij。βi0,βij,ηij,ω0i,αi為常數(shù)。

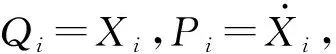
(35)

漂移與擴(kuò)散系數(shù)的表達(dá)式見附錄。

最優(yōu)控制系統(tǒng)的條件可靠性函數(shù)滿足如下的后向Kolmogorov方程：

(36)

初始與邊界條件為：

Rc(0|A10,A20,Γ0)=1,Ai0∈[0,Aic),Γ0∈[0,2π],

Rc(t|A10,A20,Γ0)=0,Ai0=Aic,

Rc(t|A10,A20,0)=Rc(t|A10,A20,2π),

i=1,2

(37)

計(jì)算中選取如下參數(shù)：βi0=βij=0.01，ω01=2.03，ω02=2.14，αi=1.0，ηij=0.2，D11=D12=D22=0.03,D21=0.004,Aic=0.5。用顯式格式的中心差分法求解偏微分方程式(33)，得到最優(yōu)控制系統(tǒng)的條件可靠性函數(shù)。圖1～2給出了一組結(jié)果。可以看到，理論結(jié)果與數(shù)值模擬比較吻合。無控制時(shí)(δi=0)，系統(tǒng)可靠性函數(shù)較小。增大控制力(δi=0.02, 0.03)，系統(tǒng)的可靠性函數(shù)得到提高。

最優(yōu)控制系統(tǒng)的平均首次穿越時(shí)間Tc(A10,A20,Γ0)滿足如下Pontryagin方程：

(38)

圖1 系統(tǒng)(34)的最優(yōu)控制條件可靠性函數(shù)

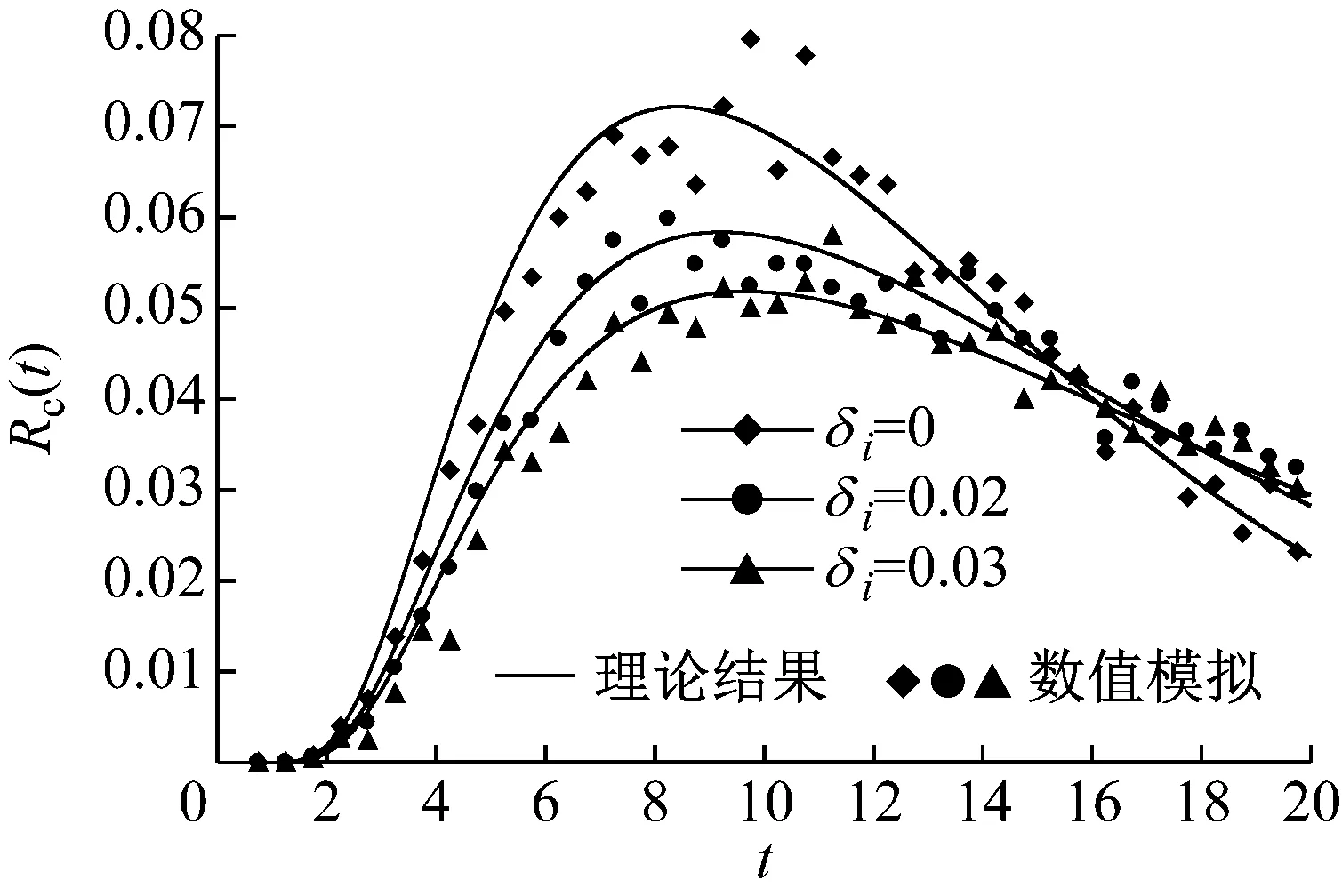
圖2 系統(tǒng)(34)的最優(yōu)控制首次穿越時(shí)間概率密度

邊界條件為：

Tc(A10,A20,Γ0)=0,Ai0=Aic,

Tc(A10,A20,0)=Tc(A10,A20,2π)，i=1,2

(39)

用中心差分法結(jié)合超松弛迭代法，求解偏微分方程式(38)，得到最優(yōu)控制系統(tǒng)的平均首次穿越時(shí)間。圖3給出了一組結(jié)果。可以看到，理論結(jié)果與數(shù)值模擬比較吻合。增大控制力，能提高系統(tǒng)的平均首次穿越時(shí)間，也即提高了系統(tǒng)的可靠性。

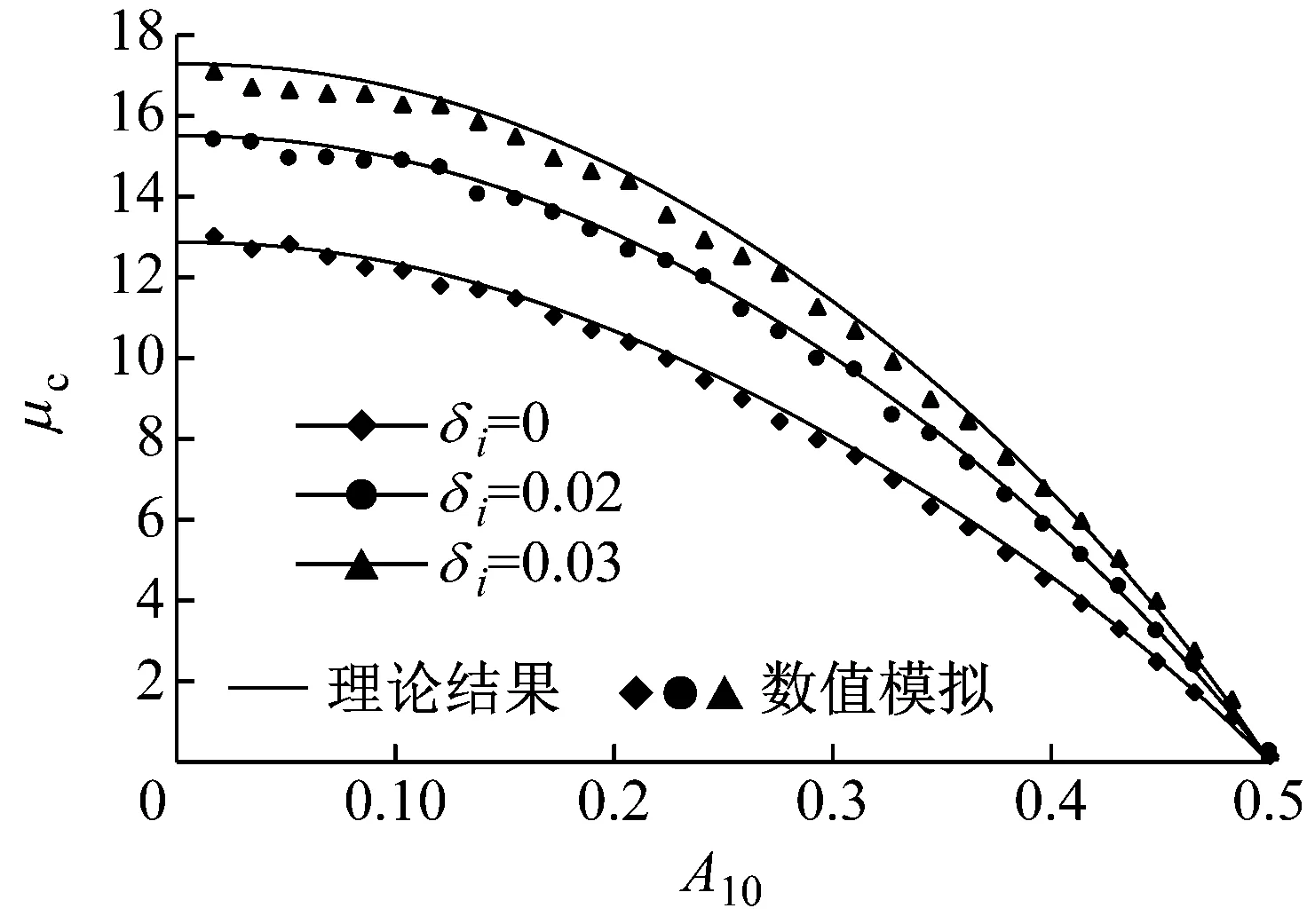
圖3 系統(tǒng)(34)的最優(yōu)控制平均首次穿越時(shí)間

5 結(jié) 論

本文研究了一類隨機(jī)激勵(lì)的多自由度非線性內(nèi)共振擬可積哈密頓系統(tǒng)的首次穿越可靠性的最優(yōu)控制問題，給出了該問題的一般性數(shù)學(xué)提法。首先基于隨機(jī)平均法，得到了內(nèi)共振情形部分平均的It隨機(jī)微分方程。定義了以可靠度最大及平均首次穿越時(shí)間最長為目標(biāo)的值函數(shù)，根據(jù)動(dòng)態(tài)規(guī)劃原理，建立了動(dòng)態(tài)規(guī)劃方程，確定了最優(yōu)控制力的形式，進(jìn)而得到了完全平均的最優(yōu)控制系統(tǒng)的It隨機(jī)微分方程。在此基礎(chǔ)上，建立了最優(yōu)控制系統(tǒng)條件可靠性函數(shù)滿足的后向Kolmogorov方程及平均首次穿越時(shí)間滿足的Pontryagin方程。以二自由度Duffing-van der Pol系統(tǒng)為例，得到了內(nèi)共振的最優(yōu)控制系統(tǒng)的平均It隨機(jī)微分方程，其漂移系數(shù)與擴(kuò)散系數(shù)不同于無內(nèi)共振系統(tǒng)。以及內(nèi)共振情形最優(yōu)控制系統(tǒng)的條件可靠性函數(shù)和平均首次穿越時(shí)間。結(jié)果表明，理論結(jié)果與Monte Carlo數(shù)值的結(jié)果較吻合，證明了理論方法的有效性。

顯然，內(nèi)共振的存在增加了數(shù)學(xué)處理的難度。在推導(dǎo)內(nèi)共振系統(tǒng)的部分平均It隨機(jī)微分方程時(shí)，除了振幅是慢變量外，還需要考慮由相位角定義的慢變量，由此得到的決定最優(yōu)控制系統(tǒng)的平均It隨機(jī)微分方程的維數(shù)更高。相應(yīng)地，需要求解更高維數(shù)的偏微分方程，以得到最優(yōu)控制系統(tǒng)的條件可靠性函數(shù)及平均首次穿越時(shí)間。另一方面，系統(tǒng)是否存在內(nèi)共振與參數(shù)選取有關(guān)。由于實(shí)際系統(tǒng)的非線性特性，導(dǎo)致系統(tǒng)頻率與系統(tǒng)的響應(yīng)有關(guān)，這與線性系統(tǒng)不一樣。一般情況下，由于系統(tǒng)的外加激勵(lì)大小的多樣性，系統(tǒng)的平均固有頻率在一定的范圍內(nèi)變化，導(dǎo)致內(nèi)共振常常無法避免。

注意到算例中，系統(tǒng)為二自由度振動(dòng)系統(tǒng)。對(duì)于實(shí)際中的機(jī)械或結(jié)構(gòu)系統(tǒng)，其自由度可能更高。本文的方法仍適用，只是需要求解更高維數(shù)的偏微分方程，需要更多的計(jì)算時(shí)間，數(shù)學(xué)處理更困難。

附錄：It隨機(jī)微分方程(35)的漂移與擴(kuò)散系數(shù)

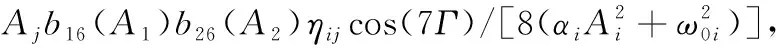
A1[2b10(A1)-b12(A1)][2b20(A2)+b22(A2)]η21sinΓ/