壩體加高對粘土心墻壩的影響研究

劉世偉，費文平，鄒海鷗

（四川大學水利水電學院，四川 成都 610065）

1 概述

粘土心墻壩作為壩工建設領域中非常常見的壩型之一，具有對地質條件要求低、就地取材、造價低、施工速度快及抗震性能好等許多優點，在當前壩工建設中得到了非常廣泛的應用。與此同時，隨著建壩的數量日益增多，由此產生的工程問題引起了國內外許多學者的關注并進行了大量研究。劉松濤[1]采用有限元方法分析了三峽茅坪溪防護工程粘土心墻方案的應力應變；姜海波[2]通過室內試驗和三軸試驗測得壩體材料的物理性質指標和鄧肯張E－B 模型參數，采用有限元方法計算并研究分析了竣工期和滲流穩定期高土石壩壩體應力、應變和變形；熊鵬、劉超群等[3]人基于鄧肯－張非線性彈性材料模型，對云南省某在建粘土心墻堆石壩逐層填筑施工和正常蓄水+9 度地震作用兩種工況情況下的壩體應力和變形進行了有限元數值模擬與分析；沈珠江、王劍平[4]運用5 種不同的土石料應力應變模型進行了數學模擬，論述了幾種模型的優缺點及土石壩應力應變分析中存在的問題。由此可見，粘土心墻壩的設計建設中，采用有限元數值模擬方法對壩體在施工和蓄水中的應力－變形進行計算與分析非常必要，已被我國壩工界所認可。本文基于鄧肯－張非線性彈性材料模型，運用有限元數值模擬方法對大壩完建工況下的壩體及粘土心墻的應力和變形進行了有限元靜力分析，以為該壩體的安全性、穩定性評價提供依據。

2 鄧肯-張E-μ 模型及二次開發

基于ANSYS 軟件的有限元計算，采用鄧肯- 張E-μ 模型，模型中的彈性模量E 的計算如下式：

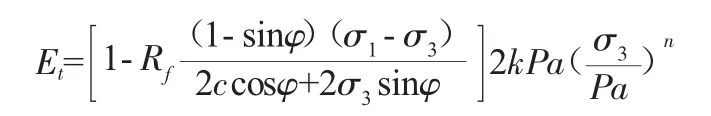
式中：c 為材料凝聚力；φ 為材料內摩角。切線泊松比μt的表達式如下：

式中：A=D(σ1-σ3)/Et、D、G、F 為材料參數。對于卸載情況，該模型采用回彈模量Eur進行計算。回彈模量表達式為：

式中：kur為卸載模量基數，nur為卸載模量指數，且一般情況下nur≈n；當σ1-σ3小于歷史上的最大值（σ1-σ3）0，且s 小于歷史最大值s 時用Eur，否則用Et。

APDL，即ANSYS 參數化設計語言,用其編寫鄧肯- 張E-μ模型的宏命令，然后賦予材料初始值，反復調用宏命令，反復計算，最終得到合理的彈性模量、泊松比，最后再計算壩體的應力應變。

3 粘土心墻壩三維有限元模型

3.1 工程概況

本文研究的是某水庫大壩的加高工程，原大壩為粘土心墻風化料壩，壩頂高程1285.40 m，最大壩高58.4 m。大壩加高選擇從下游壩坡加高培厚的方式，加高后新加高壩為粘土斜墻風化料壩，壩頂高程為1293.80 m，最大壩高66.80 m。粘土斜墻底部與原壩體心墻頂接合，斜墻底高程1281.88 m。上游斜墻壩坡1∶2.5，下游壩坡1∶2.25、1∶2.0、1∶2.0。標準剖面圖見圖1。

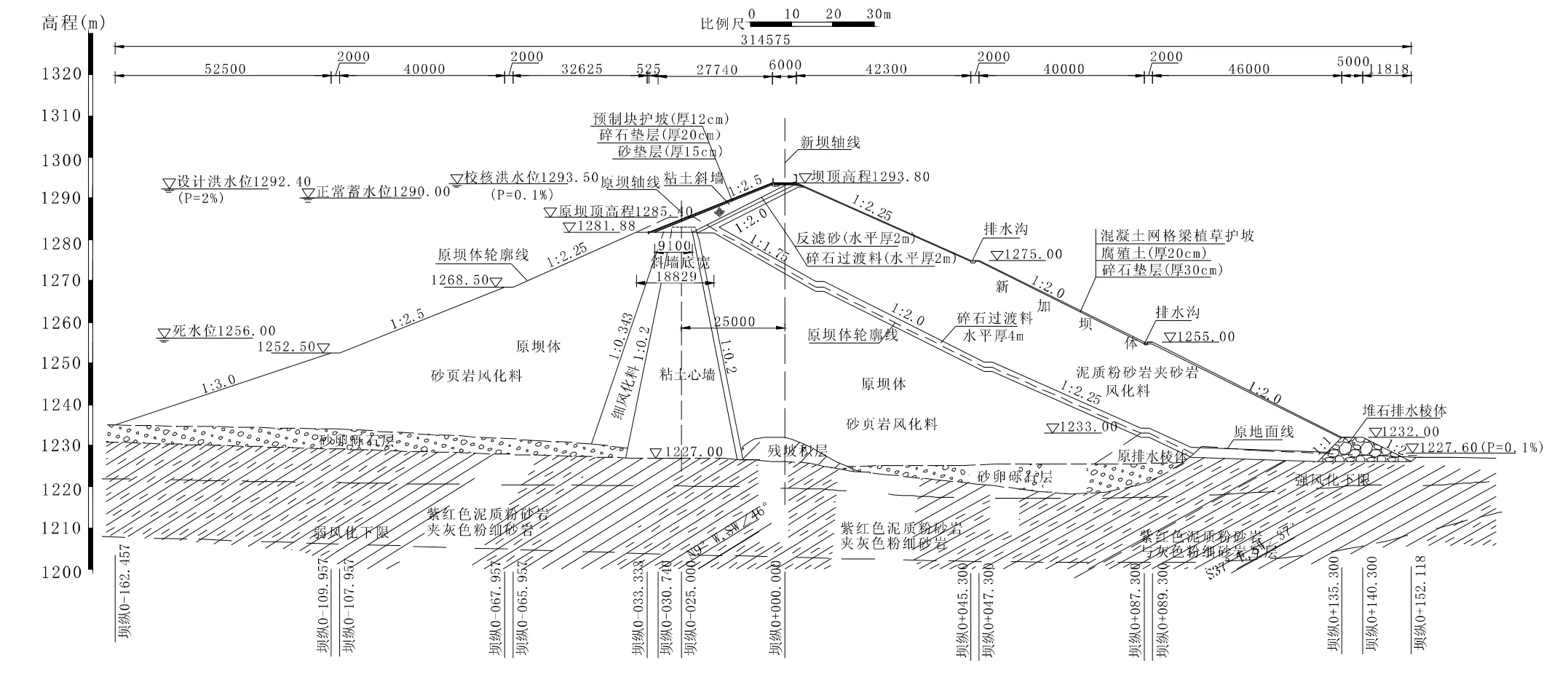
圖1 大壩標準橫剖面圖

3.2 計算參數與荷載

不考慮蓄水及其它外部條件的荷載，只考慮大壩完建期自重荷載的工況。

計算采用的單元為六面體SOLID185 實體單元，在材料參數設置上，針對不同的材料特性，靜力計算過程中主要考慮了兩種材料本構模型，對基巖采用線彈性模型，對壩體材料采用鄧肯- 張非線性模型，材料參數見表1。

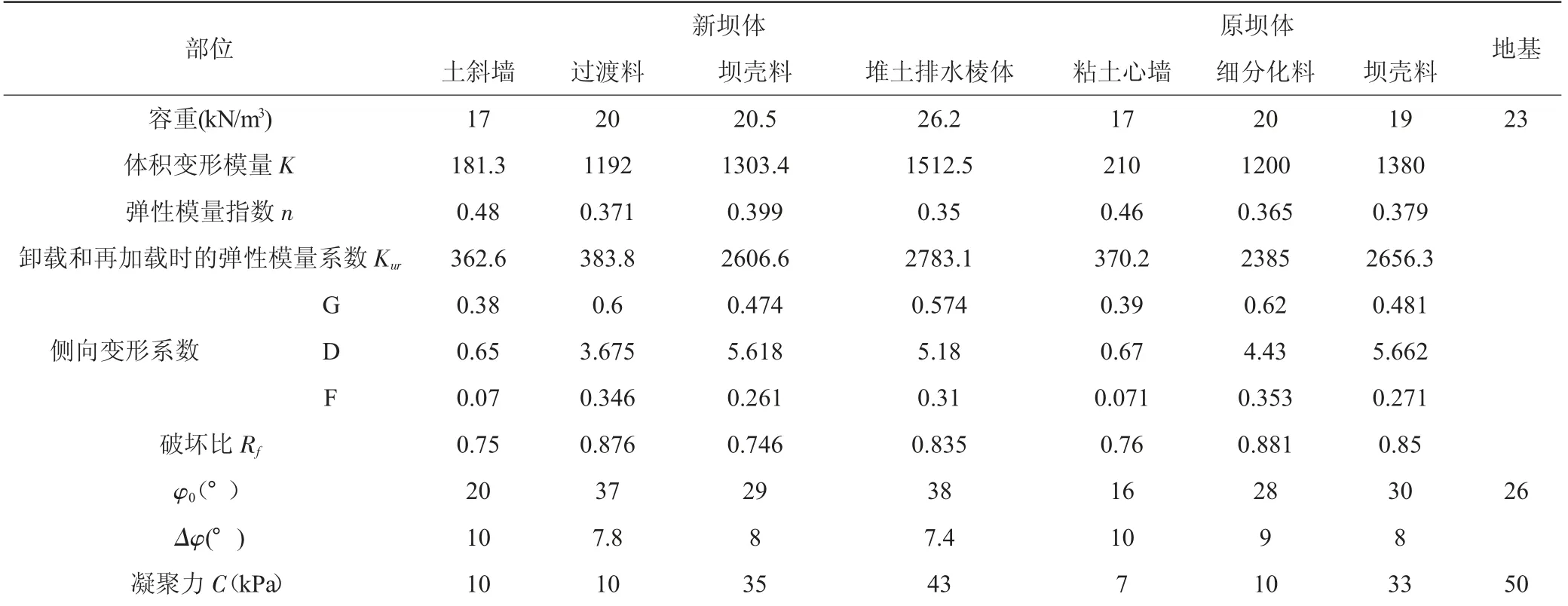
表1 壩體材料參數表（E-μ 模型參數）

對于土石壩，由于土體材料本構為非線性彈性模型，壩體最終的應力變形與加載歷史有關。因此，數值分析建模按設計加載順序分39 級加載，其中第1 級至17 級大壩填筑至1281.88 m 高程（一期填筑），第18 級至39 級大壩填筑至壩頂高層1293.80 m。根據本工程情況，建立的有限元數值模擬計算模型見圖2。

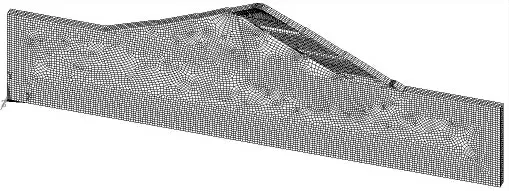
圖2 計算模型網格圖

4 擴建工程對原壩體的影響分析

4.1 擴建工程對原壩體應力的影響分析

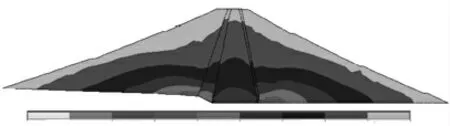
圖3 原大壩第一主應力云圖

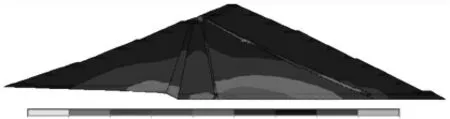
圖4 壩體加高后第一主應力云圖

圖3 表明原壩體最大拉應力為0.03 MPa，位于原壩體上游側2/3 壩高處。拉應力分布范圍極小，僅分布于最大拉應力附近。圖4 表明：加高后壩體最大拉應力為0.34 MPa，其最大拉應力位于原壩體下游側2/3 壩高處，原壩體與新建壩體的過渡區域。通過圖3 圖4 的對比可以發現，最大拉應力的分布位置和拉應力分布區域的大小發生了變化。相比加高之前只在最大拉應力位置分布有拉應力，其他位置未分布拉應力的情況，壩體加高后拉應力的分布范圍發生了變化，擴建后除最大拉應力附近有拉應力分布外，在新老壩過渡區域還分布有其他的拉應力，其分布區域從最大拉應力位置開始，沿著過渡區域向上擴展，一直到新建壩體的斜墻表面。值得注意的是，新建壩體斜墻也出現了拉應力分布，但是其數值極小為2529.72 kPa（圖4），不會危及到斜墻的安全。

圖5 原大壩第三主應力云圖

圖6 壩體加高后第三主應力云圖

圖5 表明：加高之前壩體最大壓應力為1.58 MPa，位于原壩體心墻下游側底部；壩體應力以壓應力為主，分布于各個部位，上游壩殼、下游壩殼、心墻、壩體均有分布。

圖6 表明：到大壩封頂時，壩體最大壓應力為2.20 MPa，位于壩體心墻下游側底部。壩體應力也是以壓應力為主，分布于壩體的各個部位。

對比圖5、圖6 可以看出，大壩最大壓應力出現的位置基本相同，加高后最大壓應力數值比原來增大約39%，增大幅度較大，其絕對值增加也很大，但是并未超過壩體材料的抗壓強度，不會發生危險。

4.2 擴建工程對原心墻應力的影響分析

圖7 原心墻第一主應力云圖

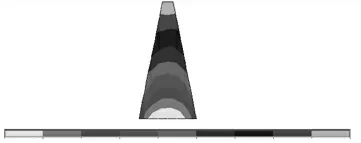
圖8 原心墻第三主應力云圖

圖8 表明：加高之前心墻最大壓應力為0.56 MPa，位于心墻底部，應力以壓應力為主，圖7 表明：未分布有拉應力。

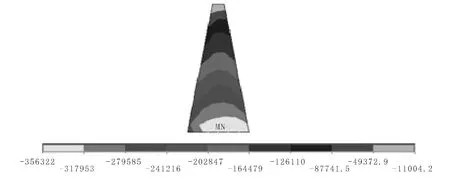
圖9 壩體加高后心墻第一主應力云圖

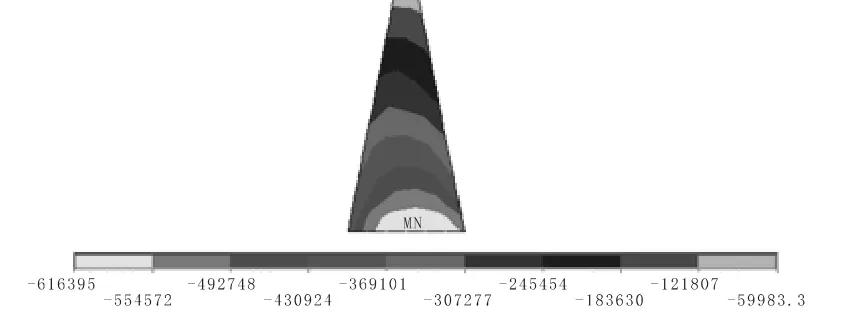
圖10 壩體加高后心墻第三主應力云圖

新壩體建成后心墻最大壓應力為0.62 MPa，位于心墻底部，應力以壓應力為主，未分布有拉應力。

心墻最大壓應力由0.58 MPa 增大為0.62 MPa，增大約7%，分布位置基本未發生變化。由此可見，壩體加高對原壩體心墻應力沒有較大影響

4.3 擴建工程對原壩體位移的影響分析

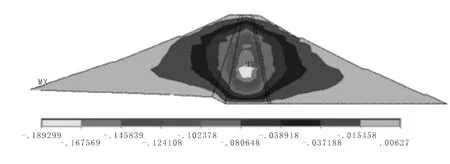
圖11 原大壩豎向位移云圖

加高前壩體最大豎向位移為18.9 mm，位于壩體中部1/3壩高到1/2 壩高處。

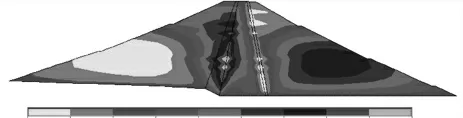
圖12 原大壩水平位移云圖

加高前壩體最大水平位移為3.3 mm，位于心墻與上游壩體過渡區域。

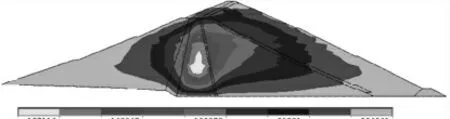
圖13 壩體加高后豎直向位移云圖

加高后壩體最大豎向位移為19.7 mm，位于壩體中部1/3壩高到1/2 壩高處。相比原來增大約4.2%。

圖14 壩體加高后水平方向位移云圖

加高后壩體最大水平位移為5.5 mm，位于心墻與下游壩體的過渡區域。相比原來增大約66.7%。其增大幅度較大，但是原來水平位移的絕對值很小。

大壩的豎向位移在加高前后變化幅度較小，絕對值也比較小；水平位移雖然增大幅度較大，但是原來壩體的水平位移本身極小，所以壩體加高對于原壩體位移的影響不大。

5 結論

基于鄧肯- 張E-μ 模型，利用ANSYS 三維有限元軟件，對某水庫擴建工程大壩計算，進行應力- 應變分析，研究擴建對大壩的影響，結論如下：

(1)原粘土心墻壩壩體最大水平位移為3.3 mm，最大沉降量為18.9 mm，最大壓應力為1.58 MPa，最大拉應力為0.03 MPa，水平位移及沉降量分布合理，壩體應力分布符合一般規律。

（2）加高后的壩體最大水平位移為5.5 mm，增大約66.7%，最大沉降量為19.7 mm，增大約4.2%，壩體加高對于原壩體位移的影響不大；最大壓應力為2.20 MPa，增大約39%，最大拉應力為0.34 MPa，水平位移及沉降量分布合理，壩體應力分布符合一般規律。壩體不會因為應力的變化出現危險。

（3）加高前、后心墻最大壓應力為0.58 MPa、0.62 MPa,增大幅度為7%。加高前后心墻均未出現拉應力，壩體加高對心墻應力的影響不大。

（4）通過對壩體加高前后的應力應變的研究，可以發現，壩體加高不會對大壩整體的穩定性和安全性有較大的影響，且加高后大壩整體變形較小，新建壩體的粘土斜墻上雖出現拉應力，但是其數值極小，斜墻開裂的可能性較小，完建工況下壩體是安全與穩定的。