合同節水管理模型對節水管理效益分配的對比研究
魯達明
(上海市供水管理處,上海 200081)
合同節水是由專業的第三方節水服務機構為合同簽訂對象提供一對一的節水服務并共享節水效益的一種新型的市場化節水機制[1]。在水資源短缺,水環境日益惡化的當下,推行合同節水不僅有利于合理開發和利用水資源,同時還能創造巨大的市場經濟效益,促進社會經濟的健康發展[2]。然而,由于合同節水在我國起步較晚,很多理論和實踐都未成熟,在推行過程中還暴露出眾多弊端,如合同節水的效益分配就是一個比較突出的問題,需要做專門的研究和探討[3-4]。
合同節水管理要注重體制機制的建立和完善,同時還應該建立統一標準,以促進合同節水向專業化邁進[5-6]。不同的社會經濟情況,需要特定的合同節水管理技術和手段,在一定程度上,由于是市場化調節,故而也存在項目的風險,即自負盈虧[7]。郭路祥等利用干系人分析和投資模式對比的方式闡述了合同節水管理投資模式的優勢,尋求可以保證合同節水管理項目投資的長效性和可持續性,以及通過利益分配的模式增強投資效能的方法[8]。鐘恒等以高效為例,對合同節水改造效益進行了分析,發現每月可較之前節水約40%[9]。尹慶民等則專門對合同節水管理的利益分配問題進行了研究,得出項目各參與方實際所得利益,對于利益分配機制的建立健全就有重要意義。本文則分別為采用Shapley 模型、修正的Shapley 模型以及公平熵模型三種方法對某用水企業、節水服務公司以及投資方三者的利益分配問題進行了對比分析研究,以期能為合同節水管理的推廣應用提供借鑒。
1 合同節水管理主要效益分配方
節水項目主要劃分為合同前準備階段,合同實施階段以及合同后期維護運行階段,見圖1。本文所研究的時間段為t1~t3,即從合同前至合同后。合同節水項目的參與方包括:節水服務公司,節水用戶,投資者,節水技術咨詢公司等相關單位,按照米切爾評分原則,以緊迫性、權利性以及合法性為評價指標對各利益相關者打分,結果見表1。從表中評分結果可以看出,從緊迫性、權力性以及合法性來講,節水服務公司、節水企業以及投資者的評分結果均為高,這說明上述三者為合同節水管理的主要效益分配方,下文將圍繞此三項進行計算分析。

圖1 合同管理時間關系
2 模型簡介
2.1 S hapley 模型
合作博弈論適用于合同節水管理的全過程,即認為節水服務公司、節水企業與投資者之間是合作博弈的過程。其滿足兩個條件,一是當沒有參與者時,不會產生合作效益,二是合作產生的效益大于各方單獨合作時的效益和。假設K、M 分別為各參與方集合和聯盟組合,ψi 表示項目參與方I 的所得利益,那么根據Shapley 的有關定理可得:

式中:|M|表示聯盟的單位數;V(M-i)表示除去參與者I 后的利益;V(K)-V(M-i)表示參與者i 的邊際貢獻值。假設節水服務公司、節水企業與投資者分別為代表第1、2、3 參與方,那么其分配利益值即可表示為φ(1)、φ(2)、φ(3)。
2.2 修正的S hapley 模型
在傳統的Shapley 模型基礎上,引入對(1)成本投入、(2)節水效果以及(3)風險承擔后果等的修正系數,其修正系數矩陣為:
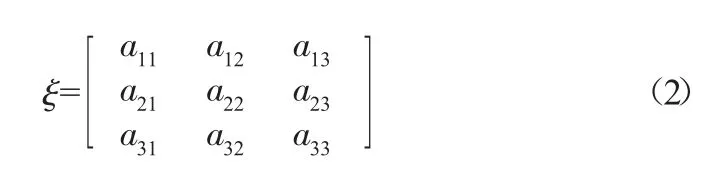
其權重矩陣為:a=|a1a2a3|T,那么由ξa 可得修正系數β,那么修正后的利益分配即可表示為:
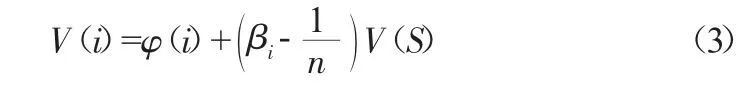
式中:V(i)表示修正后各方所得利益值,表示聯盟合作總收益。
2.3 公平熵模型
假設節水總效益為A,總投入為B,那么節水效益φ=A-B,再假設節水服務公司效益分配占比為α,那么節水企業與投資者的占比則為1-α,有:
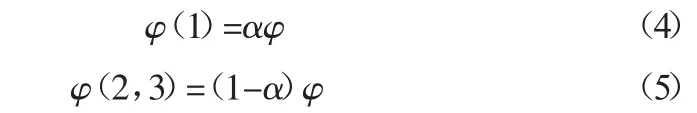

最后通過模型求解,得到:
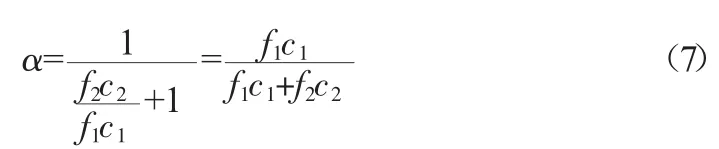
式中:f1、f2、c1、c2為計算系數且大于0,即可算出節水服務公司效益分配占比為。同理再在節水企業與投資者的節水效益值上,采用上述理論方法,分別得到節水企業與投資者的效益分配。
3 實例分析
3.1 節水項目概況
某大型國有企業分工廠(代號C),總占地面積90.2 hm2,主工廠及住宿占地面積約為50 hm2,職工人數約3200 人。由于該工廠是上世紀60 年代建立的,因此其機械設備、用水管網、生活設施等均比較老舊,經常出現跑、冒、滴、漏等現象,據統計,該工廠年均用水量約為800 萬t,年繳水費約2500 萬元,開展節水項目已刻不容緩。
節水項目主要由節水服務公司(代號P)牽頭,其擁有目前國內比較成熟的合同節水方式,能吸引各方資源及核心技術方的參與,同時積極引導某證券投資公司(代號R)設立相關的專項技術資金,即作為投資方。節水項目概算共1500 萬元,合同期為10 年,節水改造歷時約4 個月,主要完成水龍頭更新1.5 萬余只,地下管網改造約3.7 km,,在主工程及各生活區域建立多個用水監測管理平臺。合同節水改造前,其月均用水量為66.7 萬t,合同節水改造后,其月均用水量僅為43.2 萬t,節水效率達35%,年節約用水量達282 萬t,按當地水價初步計算可節約水費1100 余萬元,見圖2。

圖2 節水前后用水量對比
3.2 不同模型分配結果對比分析
(1)Shapley 模型。首先根據相關經驗及統計數據,分別作出單獨C、單獨P、單獨R,C+P、C+R、P+R 以及C+P+R7 種情況下的利益分配假設,見表2。從表中可以看出,當企業自行改造,與節水服務公司合作以及采用與節水服務公司及投資者合作時的受益值分別為總節水效益的30%、50%以及100%,而企業與投資者合作時僅產生50%的收益值。

表2 合作利益分配表
根據Shapley 模型原理,令:

即可分別得到節水服務公司、節水企業以及投資者的節水受益分配值(文中不再一一詳列)。再根據公式(1)即可分別為得到各自的收益值:
節水服務公司的收益值:

節水企業收益值:
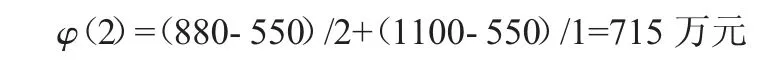
投資者收益值:

(2)修正Shapley 模型,前者已經利用Shapley 模型分別得到了三者的節水受益分配值,然后可通過專家評分,得到修正系數矩陣為:

修正影響度矩陣為:a=|a1a2a3|T,那么進一步可得修正系數:

再將其帶入公式(3)可得修正后的節水利益分配值分別為:
節水服務公司的收益值:

節水企業的收益值:

投資者的收益值:

(3)公平熵模型。由于公平熵計算過程較為復雜,文中不再贅述。通過第一次迭代得到的α(1)為0.48,第二次得到的α(2)為0.52,分別代入公式(4)、(5),即可得:
節水服務公司的收益值:φ(1)=0.48×1100=528 萬元
節水企業收益值:φ(2)=0.52×572=297.44 萬元
投資者收益值:φ(3)=0.48×572=274.56 萬元
通過對比三種模型計算得到的收益分配值,見圖3,可以看出:不同的分配計算模型對于計算結果有較大的影響,Shapley模型計算得到的收益值為節水企業最大,其次為節水服務公司和投資者,表明在此計算原則下,節水企業將得到最大的效益分配;修正的Shapley 模型計算得到的收益值結果為節水服務公司和節水企業差別不大,最小的為投資者;公平熵模型得到的結果為節水服務公司最大,節水企業次之,投資者最小,說明在此原則上節水服務公司將得到最大的節水效益分配。
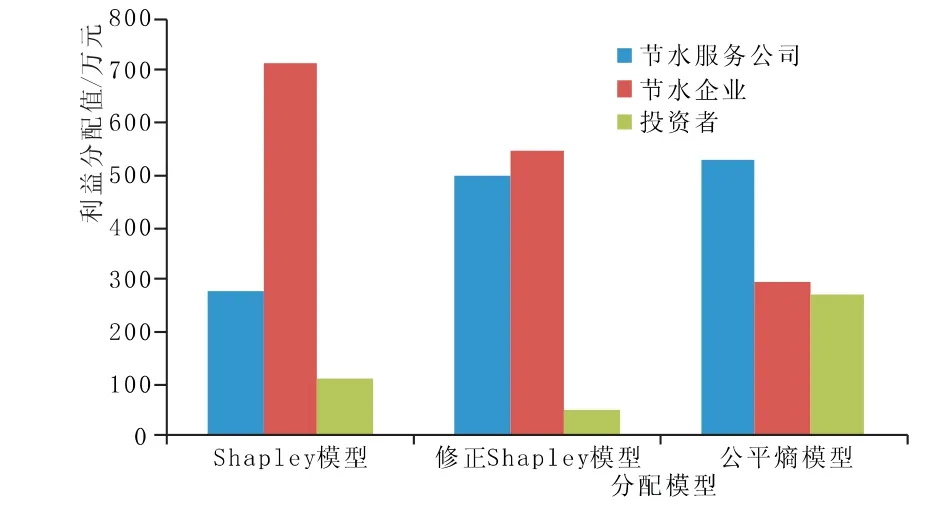
圖3 不同模型效益分配對比
4 結論
對Shapley 模型、修正的Shapley 模型以及公平熵模型三種合同節水管理模型的分配計算原理進行了介紹,并進行實證分析,結果顯示:在Shapley 模型計算原則下,節水企業將得到最大的效益分配;在修正的Shapley 模型計算原則下,節水企業和節水服務公司得到效益分配值相當;公平熵模型計算原則下,節水服務公司得到的效益分配值最大,節水企業和投資者次之。

