一種基于DCS-KF的高移動稀疏信道估計方法

袁偉娜， 王嘉璇

(華東理工大學 信息科學與工程學院， 上海 200237)

信道估計技術是無線通信技術中的重要環節，其準確與否直接影響到通信系統的整體性能，研究信道估計技術具有重要的意義。在快速移動的環境中，如高速鐵路等場景，信號頻率會產生多普勒效應，使得在1個符號周期內信道將快速變化，這樣大大增加了需要估計的信道參數的數量。對此，文獻[1-3]研究了基于小波基和基擴展模型(Basic Expansion Model, BEM)的時變信道模型，該模型可以較好地擬合快時變信道特性，降低了待估計參數數量。文獻[4]對每個正交頻分復用(Orthogonal Frequency Division Multiplexing ,OFDM)符號塊對應的快時變信道分別進行BEM建模，采用最小二乘(Least Squared, LS)和線性最小均方差(Linearly Minimum Mean Square Error, LMMSE)對BEM系數進行估計。文獻[5]考慮了信道的時域相關性，采用卡爾曼濾波(Kalman Filter, KF)對相鄰符號對應的BEM信道模型系數進行估計，獲得信道估計。而在郊區、山區等信道環境，信道多徑是由幾個具有明顯響應值的主徑和大部分響應值近似為零的徑組成，即信道多徑時延分布是零散的。如果仍然采用傳統方法，系統性能會降低。文獻[6-10]研究了基于壓縮感知(Compress Sensing, CS)算法的稀疏時不變和時變信道估計問題。文獻[11]中針對單個符號內信道響應不變而相鄰符號間變化的慢時變稀疏信道，采用KF與CS相結合的算法進行信道估計。分布式壓縮感知(Distributed Compress Sensing, DCS)[12-13]是CS的擴展，對于具有聯合稀疏性的信號組可以實現一次聯合重構。文獻[14]基于DCS研究了時不變稀疏的多入多出正交頻分復用(Multiple Input Multiple Output Orthogonal Frequency Division Multiplexing, MIMO-OFDM)系統信道估計。

上述文獻僅考慮了信道的某一個或兩個特性進行研究，本文同時考慮了符號間相關性、信道的快時變性和稀疏特性，提出了一種聯合KF和DCS信道估計的新方法。

1 系統模型

采用BEM基模型，信道響應表示為

( 1 )

式中：n=0,1,…,N-1，N定義為采樣總點數;l=0,1,…,L-1，L定義為在最大時延內的總徑數。在1個OFDM符號周期內，用h(n,l)表示第n個采樣點第l徑的信道響應；bq(n)為BEM基函數；gq(l)為BEM的系數；Q為BEM的階數。一般地，在一個OFDM符號內，BEM系數是不變的。由于基函數由一組固定的正交基組成，所以待估計的參數數量由N×L個降到(Q+1)×L個。一般情況下Q遠小于N，因此大大的降低了待估計的參數數量。

式( 1 )的BEM公式寫成矩陣形式為

( 2 )

式中：bq=[bq(0),bq(1),…,bq(N-1)]T;Gq為N×N維的Toeplitz循環矩陣；h為N×N維的時域信道矩陣。

( 3 )

( 4 )

假設系統已同步，去除循環前綴(Cyclic Prefix,CP)后，OFDM系統的時域接收信號為

( 5 )

式中：x，y分別為發送與接收的信號；w(n)為均值0，方差為σ2的加性高斯白噪的第n個采樣點；( )N定義模為N的循環移位。

式( 5 )寫成矩陣形式為

y=hx+w

( 6 )

式中：

y=[y(0),y(1),…,y(N-1)]T

x=[x(0),x(1),…,x(N-1)]T

w=[w(0),w(1),…,w(N-1)]T

則相應的頻域接收信號為

Y=FhFHX+W=HX+W

( 7 )

將式( 2 )帶入式( 7 )有

( 8 )

令Aq=Fdiag(bq)FH，式( 8 )可以表示為

( 9 )

Y=AΔg+W

(10)

再令S=AΔ，那么頻域接收信號可最終為

Y=Sg+W

(11)

2 基于DCS-KF的快時變稀疏信道估計

本文采用CS估計稀疏信道主徑位置時，需要先建立CS的觀測方程。在基于梳狀導頻的OFDM系統中，1個符號周期內的子載波數為N，導頻符號數為NP，第p個導頻符號在整個子載波的位置為Pp，p=0,1,…,NP-1。如果將發送端所有導頻信號為XP，那么相應的接收端信號YP可為

YP=HPXP+WP

(12)

式中：XP，YP為NP×1維的向量；WP是NP×1維的導頻處噪聲；HP是NP×NP維的信道頻域響應，第p個導頻位置處的信道頻響，可為

(13)

式(13)也可以用式(14)表示

(14)

因此，在1個符號周期內，可將所有導頻符號位置所對應的信道頻響為

H(P)=Φh

(15)

式中:

H(P)=[H0,H1,…,HNp-1]T

h=[h0,h1,…,hL-1]T

其中，Φp,l為NP×L維的元素，Pp為第p個導頻在子載波中的位置。

本文假設多個OFDM符號內多徑時延保持不變，則每個信道參數具有相同的稀疏部分，符合文獻[9]中介紹的適用于DCS的聯合稀疏模型，因此采用DCS估計稀疏主徑位置。

將第j個OFDM符號導頻處的稀疏信道模型為

(16)

本文假設每個符號內導頻位置相同，則每個觀測矩陣也相同。由相鄰J個OFDM符號組成的信號組對應的聯合稀疏模型為

(17)

同時正交匹配追蹤(Simultaneous Orthogonal Matching Pursuit，SOMP)算法是從最優匹配追蹤算法(Optimal Matching Pursuit，OMP)的擴展而來，區別在于SOMP每次迭代中挑選與信號組殘差最匹配的原子，建立DCS的觀測方程后，基于文獻[9]中模型采用DCS-SOMP重構算法估計稀疏主徑位置。具體步驟為

Step2最匹配原子索引為

其中,ej為單位列向量，φi為Φ第i列；

Step3更新索引集Λt=[Λt-1,λt]；

Step4計算已選原子集下信號的LS估計值為

其中,ΦΛt是Φ中與Λt對應列;

Step6如果tε，則t=t+1，重復Step1～Step5，否則迭代終止。

考慮到信道的時域相關性，采用KF算法估計BEM系數，進而獲得信道估計值。首先，采用自回歸模型(Auto Regressive, AR)[15]來表征相鄰OFDM符號間信道響應隨時間變化的線性平滑關系。為了降低算法復雜度，采用一階AR模型

hm,l=Ah,lhm-1,l+um,l

(18)

式中:hm,l定義為第m個OFDM符號內第l徑的信道時域響應向量;Ah,l定義為信道系數狀態轉移矩陣;um,l是協方差為Ul復高斯向量，表示模型誤差。

hm,l的BEM模型可以寫作

hm,l=Bgm,l

(19)

式中:hm,l=[hm(0,l),hm(1,l),…,hm(N-1,l)]T;gm,l=[g0(l),g1(l),…,gQ(l)]T;B=[b0,b1,…,bQ]定義為BEM基系數的矩陣;bq=[bq(0),bq(1),…,bq(N-1)]T。

對經過BEM轉換后的基系數建立類似AR模型

gm,l=Ag,lgm-1,l+um,l

(20)

式中:Ag,l是BEM基系數狀態轉移矩陣;um,l為協方差，Ul的模型誤差。通過尤爾-沃克(Yule-Walker)方程可以求得AR模型參數為

(21)

因為BEM系數是零均值的相關復高斯變量，其相關矩陣為

(BHB)-1BHRhl(s)B(BHB)-1

(22)

又由于本文采用的是Jakes模型信道，則

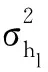
(23)

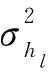
將每徑的AR模型結合，可表示為

gm=Aggm-1+um

(24)

最終將式(24)看作是KF算法狀態方程，將第m個符號所對應的頻域接收信號(見式(11))看作是KF算法的測量方程，進一步表示為

(25)

采用KF算法進行多個OFDM符號的BEM基系數估計，具體步驟為

Step1初始化

(26)

Step2時間更新

(27)

Step3測量更新

(28)

式中:gm|m-1為參數的預測值;gm為參數的估計值;Pm為估計誤差的協方差矩陣;Pm|m-1為預測估計誤差的協方差矩陣。得到多個符號的BEM系數估計值后，根據BEM模型得到主徑位置處信道估計值，其他位置處值近似為0。

3 實驗仿真

本文基于Matlab仿真平臺，對算法進行驗證。仿真中，真實信道采用符合Jakes模型的Rayleigh多徑衰落信道，QPSK調制，梳狀導頻結構，選用GCE-BEM，階數Q=2，其余參數設置見表1。重復試驗100次的平均主徑位置估計準確度為

(29)

信道歸一化最小均方誤差為

(30)

表1 仿真參數表

在歸一化多普勒頻移fnd=0.3(即移動速度v=450 km/h)的情況下，DCS和CS進行主徑估計的準確度情況，見圖1。

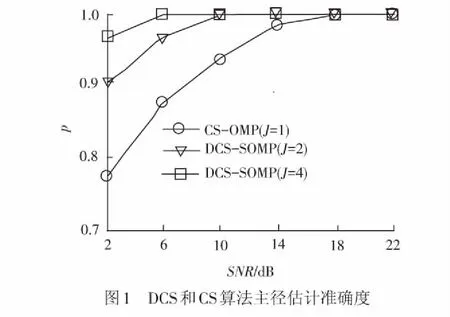
其中，CS-OMP(J=1)表示采用CS的OMP算法對單個OFDM符號進行估計，DCS-SOMP(J=2)表示采用DCS的SOMP算法對2個OFDM符號進行聯合估計，DCS-SOMP(J=4)表示采用DCS的SOMP算法對4個OFDM符號進行聯合估計。由圖1可以看出，在信噪比SNR較低時，信道噪聲干擾較大，對估計準確度有所影響。在相同的較低SNR情況下，由于使用了多符號間信道相關性，采用DCS-SOMP估計的準確度高于只針對單個符號的CS-OMP，而J=4時DCS-SOMP的估計準確度較J=2有所提高。而隨著SNR的增加，信道狀態變好，估計準確度增加，在較高SNR情況下，三者具有相近且較高的準確度。

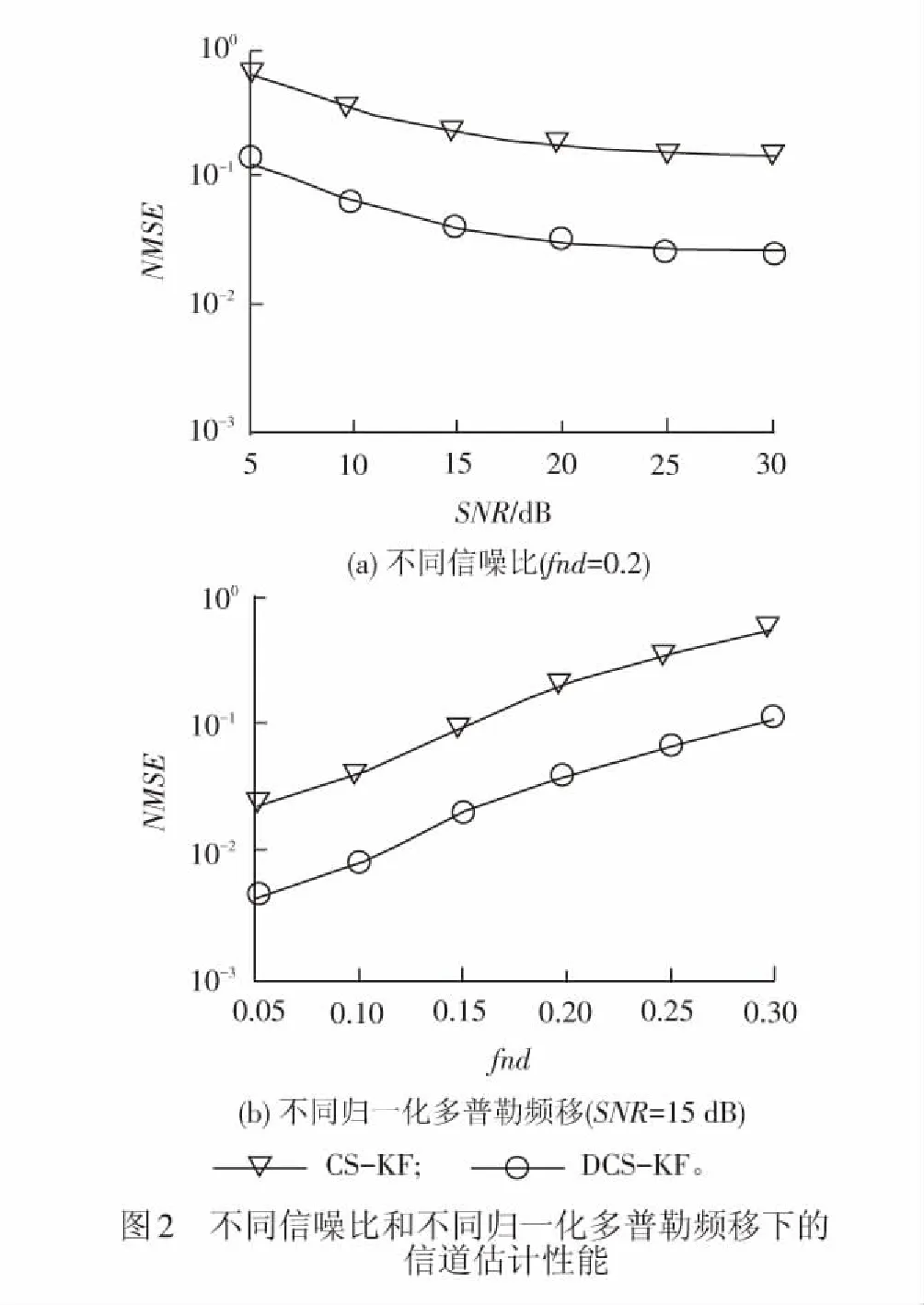
不同條件下，采用DCS和CS結合KF算法進行快時變稀疏信道估計性能見圖2。其中，DCS-KF表示采用DCS對主徑位置估計準確度高時信道估計的性能，CS-KF表示在同等條件下采用CS對主徑估計準確度低時信道估計的性能。從圖2(a)可見，在信噪比SNR=15 dB時，隨著fnd從0.05增加到0.3，對應于移動速度從75 km/h增加到450 km/h，載波間干擾增加，信道估計性能降低。從圖2(b)可見，在fnd=0.2(即移動速度v=300 km/h)時，隨著SNR增加，信道狀態變好，信道估計性能有所提高。此外，結合圖1可見，在DCS-KF主徑估計準確度比CS-KF高的情況下，其信道估計性能也優于CS-KF。

4 結束語

針對快時變稀疏環境下OFDM系統的信道估計問題，本文提出1種信道估計的新方法。新方法同時考慮到了信道的稀疏性和信道的時變性，先采用DCS技術對主徑位置進行估計，然后采用KF算法對主徑位置的信道BEM基系數進行估計，進而獲得了信道的估計值。通過仿真驗證，該方法在快時變稀疏環境下可以提高主徑估計準確度，從而提高了信道估計的性能。