黏滯阻尼器在時程分析下的附加有效阻尼比研究

吳 旭， 周美容， 陳 曦， 張雪梅

(1. 南通理工學院 建筑工程學院，江蘇 南通 226000； 2. 上海優耐建筑工程咨詢有限公司，上海 201908)

在消能減震結構中，阻尼器提供給結構的附加阻尼對結構的地震反應有顯著影響，因此，需要準確評估阻尼器的附加有效阻尼比。目前，諸多文獻[1-6]提出了黏滯阻尼器在振型分解反應譜分析或時程分析下的附加有效阻尼比的計算方法，但都是建立在一系列假設上，具有局限性，無法準確計算黏滯阻尼器的附加有效阻尼比。本文從阻尼力做功(阻尼能)的角度出發，建立在時程分析下阻尼能與阻尼比的關系，提出黏滯阻尼器附加有效阻尼比的理論計算公式，并建立有限元分析模型來驗證公式的正確性。

1 現有附加有效阻尼比計算公式

目前，根據《建筑結構抗震設計規范》(GB 50011—2010)[7]與《建筑減震消能技術規程》(JGJ 297—2013)[8]，阻尼器的附加有效阻尼比ξa可采用下式計算

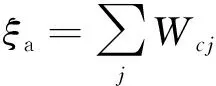
(1)

式中：Wcj為阻尼器在結構預期層間位移下往復循環一周所消耗的能量;Ws為設置消能部件的結構在預期位移下的總應變能。

本質上，式(1)是由單自由度質點固有阻尼比的原始定義ξ=c/(2mωn)推導出的[9]，但在推導過程中假設質點按自振周期做簡諧運動，以阻尼力做功Wc與總應變能Ws代替阻尼系數c、質點質量m以及圓頻率ωn來表達阻尼比ξ。因此，這種代替是建立在以下幾個前提：①結構為單自由度；②阻尼力與質點運動速度成線性關系；③質點運動模式為簡諧運動；④質點簡諧運動周期與自振周期相同(共振)；⑤Wcj,Ws分別為質點在簡諧運動往復循環一周中的阻尼器所消耗的能量與結構的總應變能。

在實際工程中，通常采用式(1)估算振型分解反應譜分析下速度相關型阻尼器的附加有效阻尼比。由于振型分解反應譜分析屬于靜力分析，分析結果雖包含結構的預期位移，但并不體現結構質點的運動模式，從而以上幾個前提并不完全成立。消能減震結構在進行振型分解反應譜法分析時，若套用式(1)來計算黏滯阻尼器的附加有效阻尼比，則自然隱含了一個假定：黏滯阻尼器是在振型分解反應譜分析得到的預期變形下按第一周期進行簡諧運動。因此，嚴格來說，采用式(1)得到結構的附加有效阻尼比為黏滯阻尼器在該運動模式下所提供的阻尼比。然而黏滯阻尼器在實際地震作用下并非按照該模式運動，此方法雖然被普遍采用，但具有局限性，并不具備明確的物理意義。

采用式(1)估算阻尼器的附加有效阻尼比時，對于位移相關型阻尼器，阻尼力僅與變形有關，可通過與結構預期位移對應的阻尼器變形來確定其所消耗的能量，并通過迭代來確定附加有效阻尼比[10-12]，因此可采用振型分解反應譜法分析。但對于速度相關型阻尼器，阻尼力與變形速度有關，無法僅由與結構預期位移對應的阻尼器變形來確定其所消耗的能量，還必須假定結構按第一周期進行簡諧運動，才能確定阻尼器所消耗的能量。所以，對于非線性速度相關型阻尼器，在進行迭代時，常無法收斂，難以獲得其附加有效阻尼比。

由于無法由振型分解反應譜分析來計算黏滯阻尼器在結構中的附加有效阻尼比，實際工程通常采用由時程分析得到的黏滯阻尼器所做的功與結構的總應變能來計算黏滯阻尼器的附加有效阻尼比[13]，并將該阻尼比返回振型分解反應譜分析來進行結構設計。常用的時程分析下黏滯阻尼器附加有效阻尼比計算公式如式(2)或式(3)

(2)

(3)

式中：Ek,max與Ep,max分別為結構在時程過程中的最大動能與最大勢能；WA與WM分別為阻尼器與振型阻尼在時程過程中累計消耗的能量；Ei為時程過程中累計輸入的總能量。

②教師地位的轉變。“互聯網+”時代的來臨，學生的獲取方式與傳播方式都發生了革命性的轉變，“不懂問百度”以成為學生的口頭禪，學生通過網絡可輕松獲得答案，教師的地位也逐漸由權威轉變為參考。網絡公開課目前呈現爆炸式發展趨勢，學生在網上就能與名師名校的距離拉近，在知識的獲取中，語文老師的權威地位受到挑戰而變得日益下降，“傳統課堂-滿堂灌”的傳播方式已經不能滿足知識日益增長的獲取方式。

然而，采用式(2)或式(3)的出發點其實是為了套用式(1)，但并不具備物理意義，原因在于：WA,WM,Ei均為整個時程過程的能量累積，Ek,max與Ep,max均為整個時程過程的最大值，并非發生在同一時刻。因此，采用此二式計算時程分析中阻尼器的附加有效阻尼比是不合理且不可靠的，若將該附加有效阻尼比返回振型分解反應譜分析來進行結構設計是不安全的。為了有效計算黏滯阻尼器在結構中提供的附加阻尼比，本文從能量角度出發，由結構運動方程重新推導附加有效阻尼比的理論解。

2 附加有效阻尼比的理論解

對于不含阻尼器的單自由度結構，運動方程為

(4)

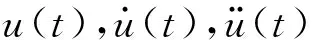
(5)

式中：cd為黏滯阻尼器的阻尼系數;α為阻尼指數。當α=1時，阻尼器為線性黏滯阻尼器，其附加有效阻尼比可套用固有阻尼比的計算公式來獲得，即：ξa=cd/(2mωn)；當α≠1時，阻尼器為非線性黏滯阻尼器，其附加有效阻尼比則無法套用固有阻尼比的計算公式來獲得。

為此，可將非線性黏滯阻尼器等效為線性黏滯阻尼器，若是基于阻尼力的等效，即：兩者在時程過程中任一時刻t的阻尼力Fd相等，則有

(6)

若是基于能量的等效，即：兩者在同一時程過程(0,t)中所消耗的能量WA相等，則有

(7)

(8)

從而可得黏滯阻尼器的附加有效阻尼比ξa為

(9)

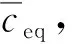
(10)

特別地，當質點按自振周期做簡諧運動時，可假設質點位移u(t)為

u(t)=u0sin(ωnt)

(11)

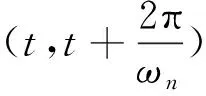
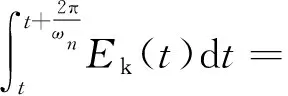
(12)

(13)

將式(13)代入式(9)，可得附加有效阻尼比ξa

(14)

此時，式(9)則退化為式(1)。對比式(1)與式(9)可見，雖然附加有效阻尼比ξa與質點動能Ek(t)在時間上的積分有關，但當質點按自振周期做簡諧運動時，質點動能在時間上的積分可用結構應變能來表示，因此，式(1)僅適用于計算質點按自振周期做簡諧運動時的附加有效阻尼比，式(9)則適用于計算任意動力荷載下的附加有效阻尼比，具有更強的適用性和合理性。

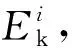
(15)

同理，振型阻尼比ξm可表示為

(16)

當時間間隔Δt越小，上式計算的阻尼比越接近真實解。

3 有限元分析驗證

現采用ETABS軟件并以一單自由度體系為例，分別驗證振型阻尼比ξm與附加有效阻尼比ξa的計算公式。該單自由度體系采用單層單跨混凝土框架結構，如圖1所示。結構跨度為6 m，高度為3 m，混凝土材料為C30，框架柱截面尺寸為400 mm×400 mm，框架梁截面尺寸為200 mm×400 mm，樓板厚度為100 mm。樓面永久荷載(含樓板自重)為4 kN/m2，樓面活荷載為2 kN/m2。在該結構中布置黏滯阻尼器，如圖2所示，阻尼器阻尼系數cd=200 N/(m/s)α，α分別取值0.1，0.2，0.3，結構振型阻尼比ξm采用0.05。地震波分別采用正弦波(周期1 s，持續時間30 s)、三角波(周期1 s，持續時間30 s)、El-Centro波(持續時間53.76 s)，ChiChi波(持續時間40 s)，進行時程分析時將結構的活動自由度限制在X-Z平面內，并將樓板設置為剛性樓板，以確保結構為單自由度。

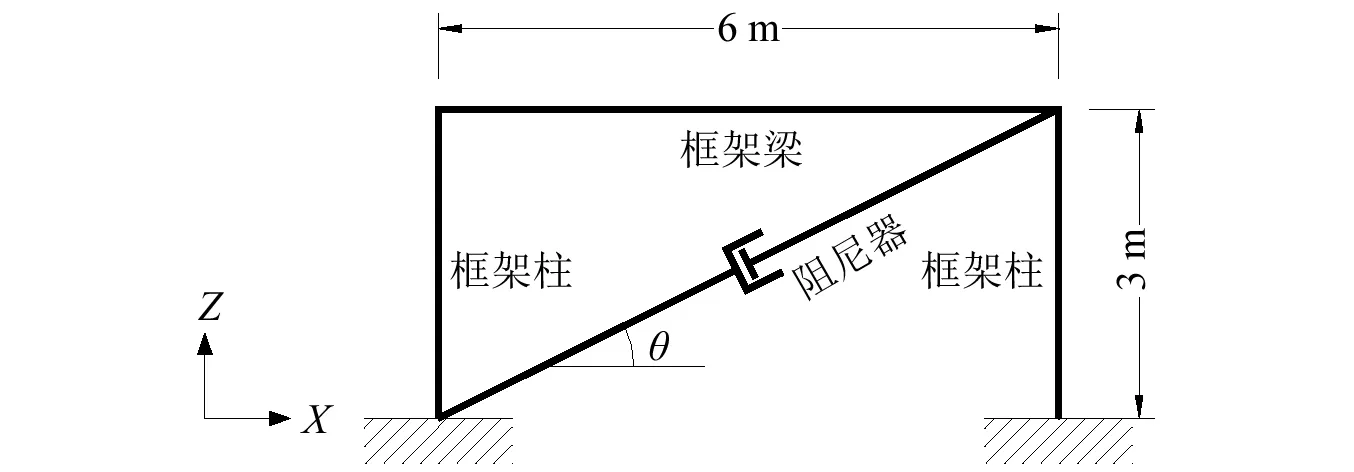
圖2 單層單跨混凝土框架結構(設置阻尼器)Fig.2 1-floor 1-bay concrete frame structure-with damper

先將時程分析結果采用式(16)計算所得的振型阻尼比ξm如表1所示。由表1可知，采用式(16)計算所得振型阻尼比ξm與已知的輸入值5.00%完全一致，證明了該計算方法的正確性，并適用于任意形式的地震波。

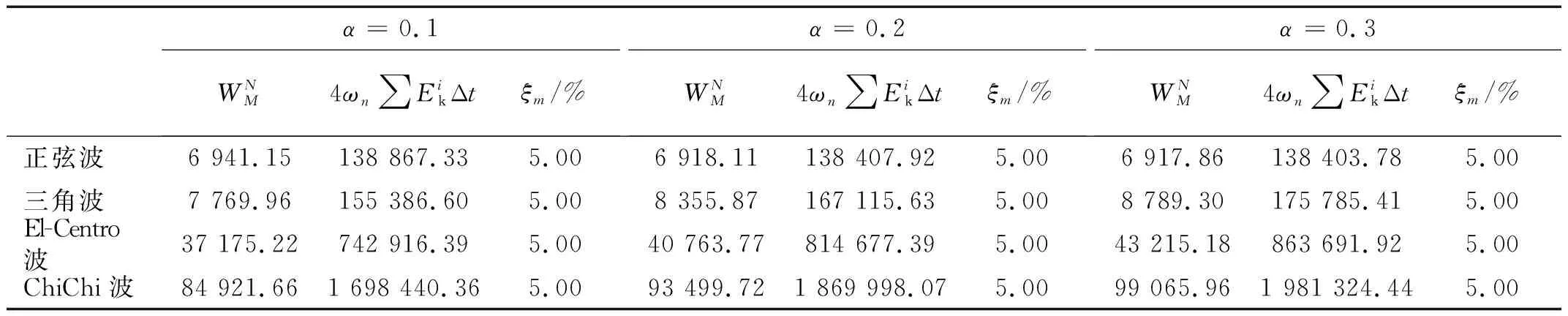
表1 振型阻尼比計算值Tab.1 Calculated values of modal damping ratio

再將α=0.2(α=0.1，α=0.3的情況不再列舉)對應的時程分析結果分別采用式(2)與式(3)計算所得的振型阻尼比ξm如表2所示。由表2可知，采用式(2)與式(3)計算所得振型阻尼比ξm均與已知的輸入值5.00%差別較大，由此可認為采用式(2)或式(3)計算黏滯阻尼器的附加有效阻尼比ξa是不合適的。

表2 振型阻尼比計算值——采用式(2)與式(3)計算Tab.2 Calculated values of modal damping ratio——using equations (2) and (3)

然后，將時程分析結果采用式(15)計算所得的附加有效阻尼比ξa分別如表3所示。由表3可知，與振型阻尼比ξm的不同在于，非線性黏滯阻尼器的附加有效阻尼比ξa在不同的時程過程是不同的。

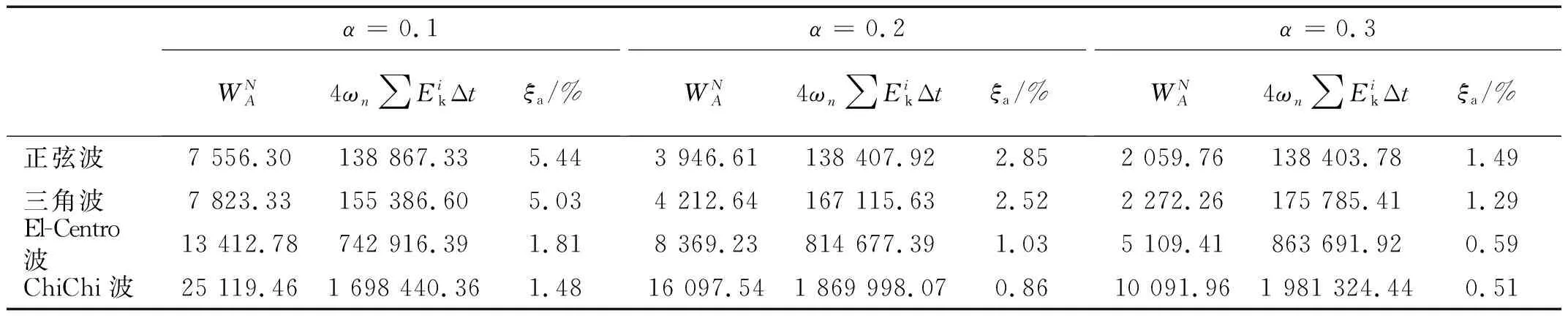
表3 附加有效阻尼比計算值Tab.3 Calculated values of additional effective damping ratio

此外，將表3中的α=0.2(α=0.1,α=0.3的情況不再列舉)對應的附加有效阻尼比ξa疊加到不設置阻尼器結構(圖1)的振型阻尼比ξm后，進行時程分析，所得的不設置阻尼器模型阻尼能WM與帶阻尼器模型阻尼能WM+WA如表4所示。由表4可知，在同一時程過程中，設置阻尼器結構的振型阻尼與阻尼器所做的功之和WM+WA，與振型阻尼在振型阻尼比為ξm+ξa的不設置阻尼器結構中所做的功WM是相等的(誤差來自有限元程序的計算精度)。因此，式(15)計算的阻尼比可視為該時程過程的附加有效阻尼比，這種等效是基于阻尼能的等效。

表4 阻尼能對比Tab.4 Comparison of damping energies

最后，對比式(9)與式(10)可得，當振型阻尼比ξm為已知時，可直接通過黏滯阻尼器與振型阻尼所做的功的關系來確定附加有效阻尼比ξa，即

(17)

雖然式(17)是建立在單自由度結構的前提下推導出的，但也同樣適用于多自由度結構。將時程分析結果采用上式計算所得的附加有效阻尼比ξa如表5所示，可以看出，采用上式計算所得的附加有效阻尼比與采用式(16)計算結果完全一致，因此，當結構振型阻尼比ξm已知時，采用式(17)確定附加有效阻尼比更加便利。

表5 附加有效阻尼比計算值Tab.5 Calculated values of additional effective damping ratio

4 結 論

(1)現有的消能減震結構附加有效阻尼比計算公式(1)是由單自由度質點固有阻尼比的原始定義推導出的，假設質點按自振周期做簡諧運動，并以能量的形式來表達的。因此，該公式具有局限性，不適合用于計算消能減震結構在時程分析中黏滯阻尼器的附加有效阻尼比。

(2)實際工程中常用的消能減震結構在時程分析中黏滯阻尼器的附加有效阻尼比的計算式(2)與式(3)不具備物理意義，所計算的附加有效阻尼比是不合理且不可靠的。

(3)本文基于能量的等效，將非線性黏滯阻尼器等效為線性黏滯阻尼器，提出黏滯阻尼器的附加有效阻尼比計算公式，該公式經由已知的結構振型阻尼比驗證了其正確性，適用于計算任意動力荷載下的附加有效阻尼比，具有更強的適用性和合理性。

(4)本文提出的計算公式所計算的非線性黏滯阻尼器的附加有效阻尼比在不同的時程過程是不同的。

(5)將本文提出的計算公式所計算的附加有效阻尼比疊加到不設置阻尼器結構的振型阻尼比后，其振型阻尼做所的功，與消能減震結構在同一時程過程下的振型阻尼與阻尼器所做的功之和相等，因此，本文提出的計算公式所計算的附加有效阻尼是基于阻尼能的等效。

(6)當振型阻尼比為已知時，可直接通過黏滯阻尼器與振型阻尼所做的功的比值關系來更加便利地確定附加有效阻尼比。