曲線鋼橋單梁模型與板單元模型計算比較

張 君

(中國建筑東北設計研究院有限公司 沈陽市 110000)

1 引言

在我國發展快速交通的大趨勢下，橋梁需求日益增加，傳統的鋼筋混凝土結構橋梁由于建設周期長、跨徑受限大、不利于環保等因素，使用上受到諸多限制，鋼箱梁橋、鋼板梁橋、組合梁橋、鋼桁架橋等鋼結構橋顯示了巨大的優勢。

鋼橋具有很大的跨越能力，鋼材可加工性能好，構件可工廠加工預制，便于無支架施工，工地的安裝速度快，施工工期較短，便于修復更換，舊橋可回收，有利于環保。未來我國橋梁的發展，無論公路還是市政，鋼橋的使用比重會越來越大。

曲線鋼橋一般位于平面線形的圓曲線或者緩和曲線上，受力較為復雜，計算時應進行空間有限元分析，而如何快速、精確地建立模型并計算，需要設計人員對各種曲線橋有深刻的理論認識和豐富的經驗。

以沈陽市五愛立交橋一聯寬7m、跨徑30m+40m+30m曲線鋼箱梁為例，有限元分析采用兩種建模方式：空間單梁模型與空間板單元模型，并對兩種方法的計算結果進行了對比，以此為例，對類似的曲線鋼橋計算提供簡化、借鑒。

2 曲線鋼箱梁概況

曲線鋼梁橋寬7m，為單箱三室斷面，梁高(中心處)2.095m。外側腹板斜腹板，并與翼緣板、底板采用半徑0.5m圓弧過渡。標準段橫坡為單向2%。

鋼箱梁頂板厚16mm、24mm，腹板厚16mm，底板厚16mm、36mm，頂板縱向加勁肋采用倒T肋，厚12mm，底板縱向加勁肋采用板肋，厚12mm。

曲線鋼梁大部分位于半徑60m的圓曲線上，兩側30m邊跨均進入緩和曲線；中跨40m在圓曲線上。

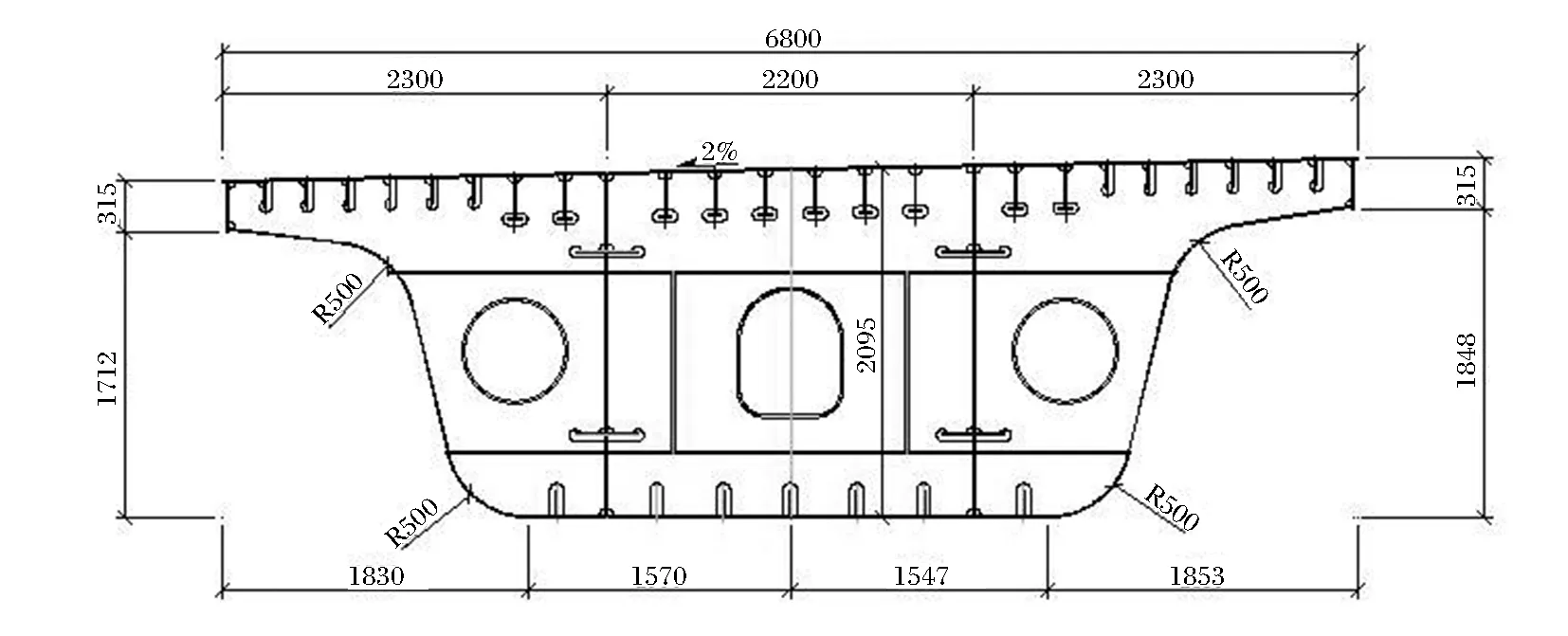
圖1 曲線段7m寬鋼箱梁橫斷面圖

3 曲線鋼箱梁有限元計算

曲線鋼梁有限元計算采用兩種建模方式：空間單梁模型與空間板單元模型。如圖2、圖3所示：

圖2 曲線鋼箱梁梁單元模型

圖3 曲線鋼箱梁板單元模型

單梁模型采用梁單元建模，二期荷載通過虛擬梁加載，這樣也將內外弦防撞墻、鋪裝等二期恒載偏差區別出來，計算結果更加準確，符合實際情況。活載通過車道線荷載進行加載。

板單元模型根據實際情況建模，防撞墻等二期恒載與單梁模型保證一致，方便對比。活載采用車道面進行加載。

4 計算結果對比

4.1 支座反力對比

對兩種建模方式的計算結果的自重、鋪裝、防撞墻、最大活載反力進行對比，溫度等其它荷載數值占比較小略過。

為更加直觀比較表1中的數據，將表1以折線圖表形式表達如圖4～圖7。

由表1可知，自重誤差1%，鋪裝誤差0.007%，防撞墻誤差0.51%，最大活載誤差6.25%，均在10%以內。自重由于曲線內外弦長度誤差控制在1%可以說很理想，而二期恒載誤差基本可以忽略不計，只有活載誤差較大，這是由于單梁模型并沒有區別曲線車道的加載長度，單梁計算結果大于板單元模型計算結果。

表1 兩種模型計算結果支反力對比表

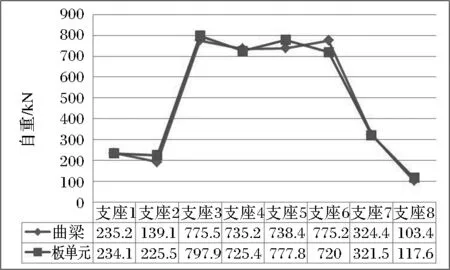
圖4 自重支反力比較

圖5 鋪裝支反力比較

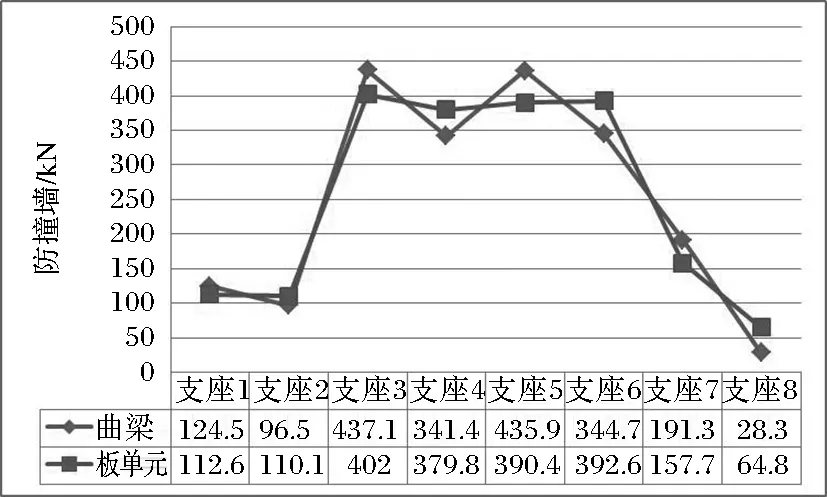
圖6 防撞墻支反力比較

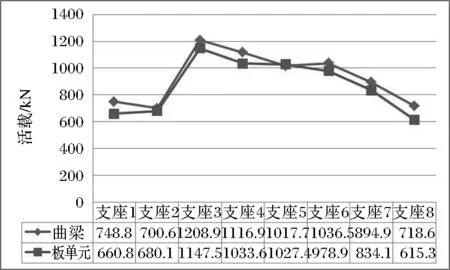
圖7 最大活載支反力比較

另外，值得我們注意的是中跨支座5、6，曲線單梁計算結果外弦支座支反力小于內弦支座支反力，板單元計算結果則相反，盡管曲線單梁與板單元計算結果誤差不大，但兩者規律相悖，板單元模型顯然更符合實際情況。所以，在用梁單元計算曲線跨時，需注意支反力規律的異常。

還有，在研究曲線連續梁在重力作用下支座支反力規律的很多論文中，邊跨比大于0.55時，邊墩外側反力大于內側反力，邊跨比小于0.55，則相反，而中墩則一般情況均是外側小于內側，這個規律與第一種曲線梁單元模型的計算結果規律一致；這是由于在研究時，無論是微積分計算還是建模計算都是按相同截面內外弦一致，所以與第一種曲線梁單元計算結果規律一致。實際上，由于是曲線，內外弦長度不等，只有板單元、實體單元有限元計算才更加符合實際情況。但梁單元的計算結果依舊可以參考，因為誤差很小，僅是規律相反。

4.2 鋼箱梁應力計算結果對比

為了精確、直觀地比較兩種模型計算結果差異，應力計算結果對自重等主要單項荷載結果進行了對比。

第一種曲線梁單元計算模型，自重、鋪裝、防撞墻、最大活載、最小活載應力計算結果如圖8所示。

圖8 曲梁自重應力計算結果

曲梁自重應力計算結果：最大拉應力12.8MPa，最小壓應力-23.1MPa。

曲梁鋪裝應力計算結果：最大拉應力4.5MPa，最小壓應力-8.1MPa；曲梁防撞墻應力計算結果：最大拉應力6.6MPa，最小壓應力-11.9MPa。限于篇幅，計算圖略。

圖9 曲梁最大、最小活載應力計算結果

曲梁最大、最小活載應力計算結果：最大拉應力34.5MPa，最小壓應力-38.5MPa。

第二種板單元計算模型，自重、鋪裝、防撞墻、最大活載、最小活載應力計算結果根據第一種曲線單梁結果可知2#墩墩頂壓應力最小，中跨跨中拉應力最大，對應板單元應為底板位置單元，在板單元模型中找到同位置對應板單元計算結果，底板板單元計算結果如圖10所示。

圖10 板單元模型底板單元自重應力計算結果

板單元模型底板單元自重應力計算結果：最大拉應力14.3MPa，最小壓應力-28.3MPa。

板單元模型底板單元鋪裝應力計算結果：最大拉應力5.3MPa，最小壓應力-10.1MPa；防撞墻應力計算結果：最大拉應力7.7MPa，最小壓應力-14.7MPa；活載應力計算結果：最大拉應力39.5MPa，最小壓應力-32.3MPa；限于篇幅，計算圖略。

梁單元與板單元計算結果是底板計算結果，故鋼梁第二體系基本沒有影響，所以可以進行直接比較，兩種模型應力計算結果比較如表2所示：

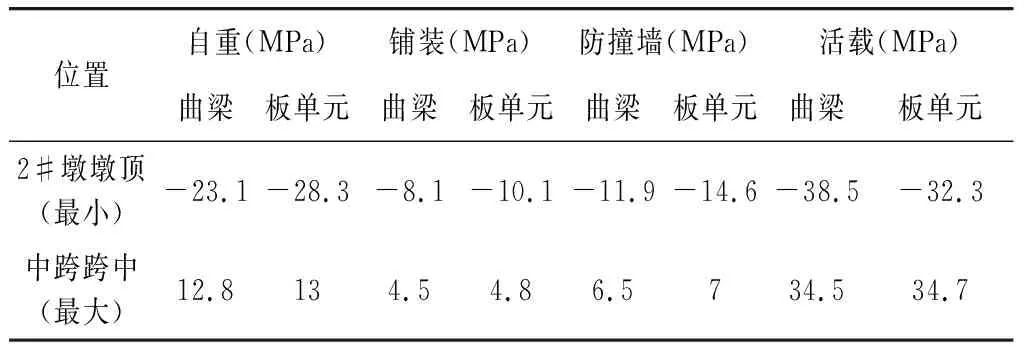
表2 兩種模型應力計算結果比較

由表2可知，中跨跨中最大拉應力計算結果基本一致，誤差很小；而支點負彎矩區域相對誤差較大，最大相差6.2MPa。組合之后，誤差更小一些。

但活載計算按雙車道進行計算的，實際7m寬橋車道數為一車道，活載誤差實際更小。

5 結論

綜上，我們可以得出以下結論：

(1)曲線單梁計算結果與板單元計算結果相比，自重、二期恒載略小，活載略大，組合之后曲梁模型計算結果略大于板單元模型，誤差在10%以內。

(2)曲線單梁模型與板單元模型，邊跨邊墩支反力規律為外弦支座支反力大于內弦支座支反力。需注意與邊跨比有關，一般適用邊跨比大于0.55時。

(3)曲線單梁模型中，一般情況下，中跨中墩支反力規律為外弦支座支反力小于內弦支座支反力。

(4)曲線橋板單元模型中，一般情況下，中跨中墩支反力規律為外弦支座支反力大于內弦支座支反力。

(5)當橋寬較小，車道數較少時，曲線梁單元模型完全可以指導設計；而當橋寬較寬，車道數較多時，由于內外弦長度誤差增加，梁單元就無法完全反饋出來，建議鋼橋建立板單元模型進行分析計算。

(6)曲線鋼橋，一般情況下頂板計算結果不控制，但當中跨跨徑增大，邊跨比變小時，頂板計算結果開始控制計算時，還需要注意鋼梁第二體系計算結果的疊加，避免計算結果取值過于極限；當然也要避免過于保守，做到充分利用鋼材的性能，也保證橋梁的安全。

(7)鋼橋設計時，建議負彎矩區即橋墩墩頂處，鋼梁內配置一定高度、寬度混凝土，既可配重，又改善橋梁性能。

(8)鋼橋設計時，建議橋面鋪裝層盡量能改善橋面系疲勞問題。