一種改進的四旋翼飛行器建模方法

劉士超，呂 品，賴際舟，包 勝

（南京航空航天大學自動化學院，南京211106）

0 引言

近年來，隨著四旋翼飛行器相關技術的發展，其被廣泛應用于軍事、民用領域［1］。目前，四旋翼飛行器通常采用 PID控制算法［2?3］。然而，隨著四旋翼飛行器飛行任務的多樣化、飛行環境的復雜化［4］，其對控制算法的抗干擾性提出了越來越高的要求。針對于此，研究人員將自適應控制等基于模型的控制算法應用于四旋翼飛行器。文獻［5］、文獻［6］提出在建立四旋翼飛行器動力學模型的基礎上，采用自適應控制算法對四旋翼飛行器的姿態、位置進行控制。對于這類控制器，準確的動力學模型是保障控制精度的重要前提。

目前，四旋翼飛行器的動力學建模普遍是在直升機旋翼模型的基礎上推導的，其主要考慮了單旋翼的動力學特性。文獻［7］、文獻［8］基于旋翼的葉素理論和動量理論，對單旋翼所產生的升力、阻力、扭矩模型進行了推導，建立了四旋翼飛行器的動力學模型。文獻［9］提出了基于葉素理論和動量理論的旋翼飛行器的氣動力模型（包括升力模型和阻力模型），并且在水平側飛的過程中，使用阻力模型進行了水平速度估計。文獻［10］提出了基于升力模型的旋翼飛行器高度信息容錯估計，該升力模型是在單旋翼基礎上得到的，忽略了飛行器整體的動力學特性。文獻［11］、文獻［12］通過對單旋翼空氣動力學進行分析，推導出了四旋翼飛行器在機動性較小或懸停狀態下的動力學模型。上述文獻僅考慮了單旋翼的氣動力特性，而忽略了飛行器在機動飛行時所呈現出的整體動力學特點。本文對四旋翼飛行器傳統的動力學模型進行了改進，使其能夠更好地描述四旋翼飛行器的動力學特性，相應結論通過試驗得到了驗證。

1 四旋翼飛行器的動力學建模及改進

四旋翼飛行器受力分析是建立其動力學模型的基礎。本文所使用的坐標系為導航系和機體系，其中導航系選為東北地坐標系，機體系選為前右下坐標系，如圖1所示。四旋翼飛行器在運動過程中所受到的力包括升力、阻力和重力，所受到的力矩包括扭矩、橫滾力矩和俯仰力矩。這些力與力矩主要與旋翼轉動有關，是分析四旋翼飛行器運動的基礎［13］。

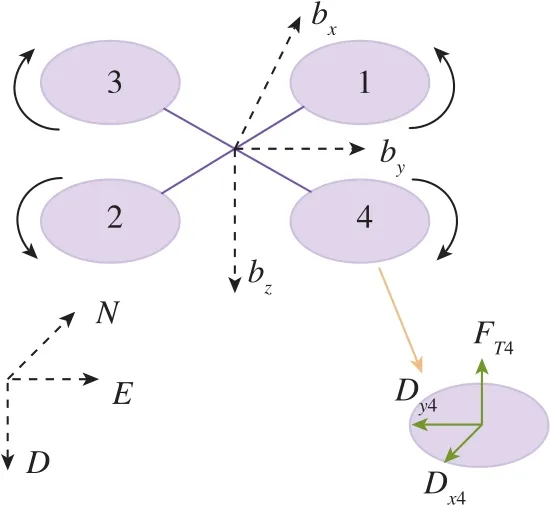
圖1 四旋翼飛行器的受力示意圖及坐標系定義Fig.1 Force diagram of quadrotor and frame definition

1.1 四旋翼飛行器升力、阻力模型建模

四旋翼飛行器是欠驅動系統，通過4個旋翼的轉速來調整自身的姿態和運動速度［14］。在飛行過程中，每個旋翼都受到升力、阻力的作用。在近年的研究中，已經建立了簡化的四旋翼飛行器的動力學模型。文獻［15］、文獻［16］提出了旋翼飛行器的升力、阻力、扭矩、力矩模型，這些模型均是基于單旋翼特性且在水平側飛或懸停狀態下提出的，本文將其稱為傳統動力學模型，采用上標的“tra”表示。本文提出的四旋翼飛行器改進動力學模型采用上標的 “im”表示。

（1）四旋翼飛行器的傳統升力、阻力模型

①升力模型

升力由旋翼旋轉產生，方向垂直旋翼平面且沿著機體系的z軸方向向上。根據單個旋翼的升力特性，四旋翼飛行器所受到的升力表達式如下［17?18］

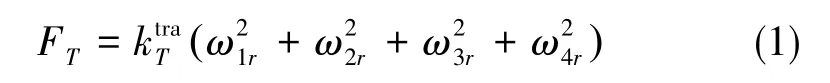
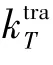
②阻力模型

四旋翼飛行器的阻力主要來源于輪轂力，輪轂力是四旋翼飛行器在做側向運動時作用于旋翼上的力，其方向與旋翼葉面平行且與飛行器運動方向相反，其表達式如下［17，19］

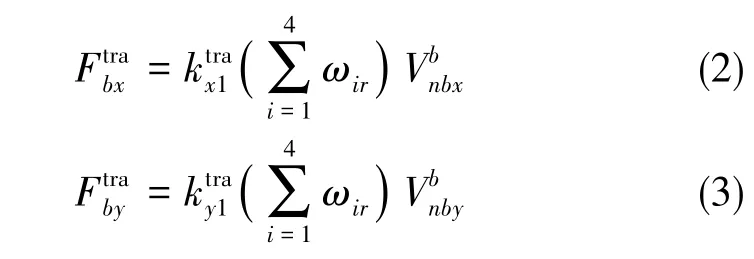
（2）四旋翼飛行器的改進升力、阻力模型

①改進升力模型

受機體加工誤差的影響，四旋翼飛行器的升力模型在式（1）的基礎上呈現出了一定的常值偏置特性。針對于此，提出以下的改進升力模型

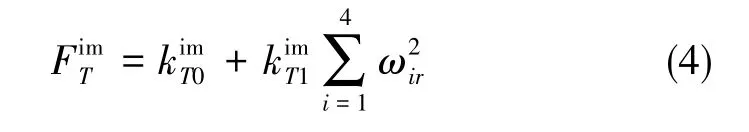
②改進阻力模型

傳統的阻力模型僅考慮了四旋翼飛行器在側飛運動過程中旋翼的側力特性。當四旋翼飛行器進行橫滾、俯仰的角運動時，其旋轉中心通常在飛行器的質心位置，而旋翼與旋轉中心存在一定距離。此時，旋翼會敏感到由角運動引發的切向力。此外，受機體加工誤差的影響，阻力模型也會存在一定偏置。改進的阻力模型如下所示

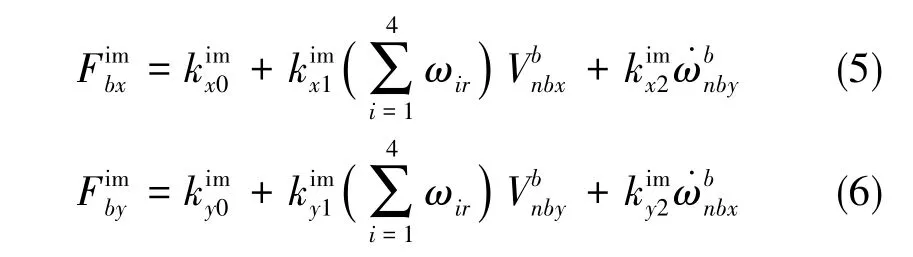
相較于傳統的動力學模型，改進的升力模型和阻力模型增加了零偏項，該項的增加可以解決飛行器加工及器件加工的誤差問題。同時，針對飛行器的轉動飛行狀態，在阻力模型中加入了角加速度相關項，使得改進的動力學模型適用于大機動性運動，突破了傳統模型的低速平飛或懸停運動的限制。

1.2 四旋翼飛行器力矩模型建模

四旋翼飛行器所受力矩包括扭矩、橫滾力矩和俯仰力矩，其通常由升力、阻力引起。

（1）四旋翼飛行器的傳統力矩模型

①扭矩模型

旋翼在轉動過程中，由于空氣阻力作用，會形成與轉動方向相反的反扭矩。為了克服反扭矩的影響，通常令2個旋翼正轉，2個旋翼反轉。當4個電機轉速不完全相同時，不平衡的反扭矩會引起四旋翼飛行器繞機體系z軸轉動。其可表達為如下形式［20?21］

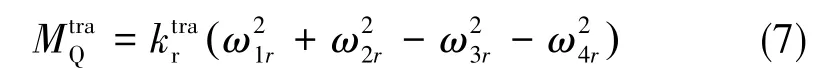
②橫滾、俯仰力矩模型

在傳統的橫滾、俯仰力矩模型中，其通常僅考慮由旋翼的升力而產生的力矩。因每個旋翼產生的升力不同，其會產生如下形式的力矩［20?21］

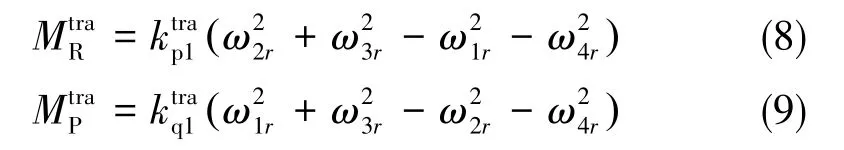
（2）四旋翼飛行器的改進力矩模型

①扭矩模型

當四旋翼飛行器繞機體系z軸進行旋轉時，旋翼會敏感切向速度，從而產生阻力。由于該阻力在旋翼中心，距轉動中心有一定距離，因此會產生扭矩，其可表示為

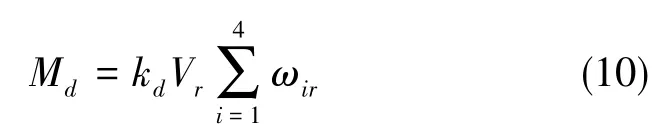
式中，Md是四旋翼飛行器所受到的阻力矩；kd是阻力矩系數；Vr為旋翼在轉動半徑R處的線速度，Vr=ωbzR；ωbz為機體系相對于導航系的角速度在機體系z軸上的分量，將其帶入式（10）可得到

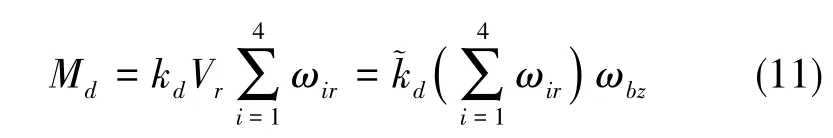
考慮零偏，則四旋翼飛行器的改進扭矩模型可以表達為如下形式

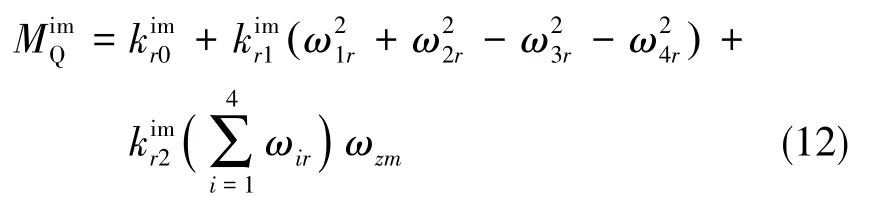
②橫滾、俯仰力矩模型

當四旋翼飛行器做橫滾和俯仰轉動時，其會受到切向力的作用。該切向力與飛行器轉動軸之間存在一定距離，從而會產生橫滾、俯仰力矩，該力矩可表示為

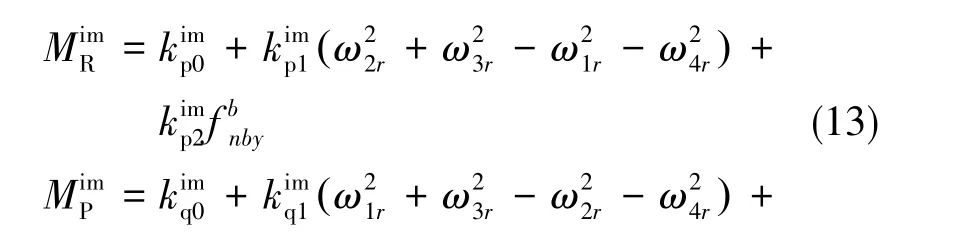
針對旋翼飛行器的力矩及扭矩改進模型，考慮到飛行器結構的安裝誤差，需增加零偏項。同時，考慮到運動過程中整體的動力學特性，需在扭矩模型中增加阻力項，在力矩模型中增加切向力項，這在一定程度上提高了模型的精度，實現了模型的優化。

1.3 四旋翼飛行器改進動力學模型分析

綜上，四旋翼飛行器改進的動力學模型可以表達為

相對于傳統模型，改進模型考慮到了四旋翼飛行器的安裝誤差，在動力學模型中加入了零偏項，同時考慮到了四旋翼飛行器在做側飛、旋轉等機動飛行時的整體動力學特性。通過增加四旋翼飛行器在轉動飛行時所受側力的角加速度項、扭矩的阻力項、橫滾和俯仰力矩的切向力項，可以更好地對四旋翼飛行器動力學特性進行描述。

2 試驗及分析

為了對本文所提出的四旋翼飛行器動力學模型進行驗證，本文進行了多種機動下的飛行試驗，其飛行場景如圖2所示。飛行試驗所采用的四旋翼飛行器的基本參數如表1所示。

圖2 室外試驗場景圖Fig.2 Outdoor test scene

表1 四旋翼飛行器的基本參數表Table 1 Basic parameters of the quadrotor

在飛行試驗中，其航跡設置如表2所示。即首先進行60s的懸停運動，其次進行上下往返運動，之后進行橫滾、俯仰運動，然后進行航向轉動，最后進行橫滾方向的側飛運動和俯仰方向的側飛運動。

在飛行試驗中，陀螺、加速度計、GPS可以對飛行器的角速度、加速度、速度信息進行記錄。通過對角速度進行微分，可以得到角加速度的信息。由四旋翼飛行器的動力學方程可知，其加速度、角加速度與力、力矩是成正比的。因此，通過對式（15）進行轉換，可以得到四旋翼飛行器加速度、角加速度的計算表達式，如式（16）所示。

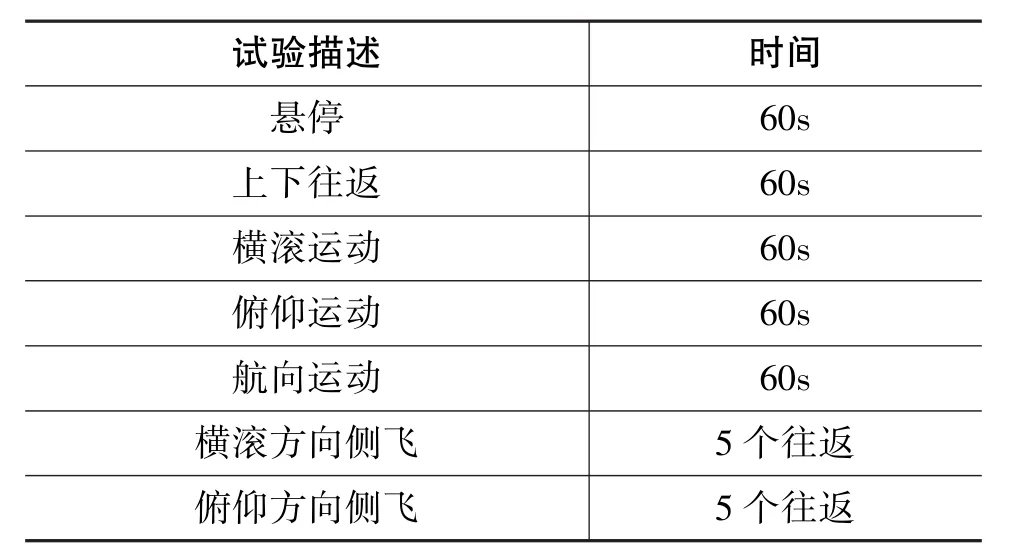
表2 模型對比驗證的試驗航跡設置Table 2 Test track setting of model comparison verification test

對傳統的動力學模型進行轉化，可得到傳統動力學模型的加速度、角加速度表達式

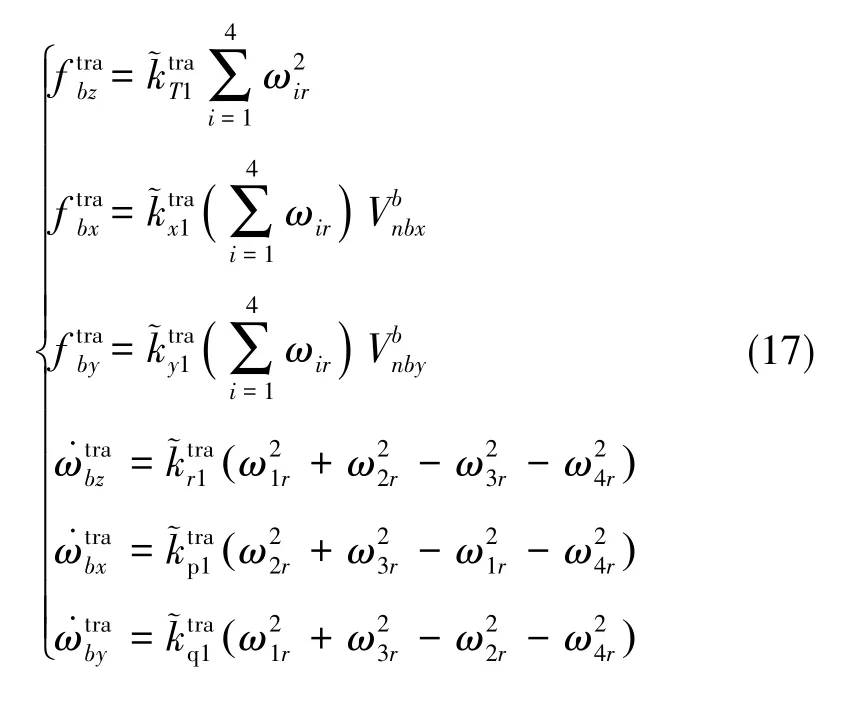
通過式（16），對四旋翼飛行器的加速度、角加速度模型進行擬合，通過將其與傳統模型的擬合結果進行對比，可以對兩種模型的準確性進行評價。

本文采用擬合優度的概念對兩種模型的擬合精度進行分析。擬合優度描述了所構建的模型與觀測數據集的匹配程度，可以用來衡量所建立的模型的準確度。衡量擬合優度的統計量為確定系數R2，其取值范圍為［0，1］。擬合優度越接近1，意味著所建立的模型越準確，其定義如下［22?23］

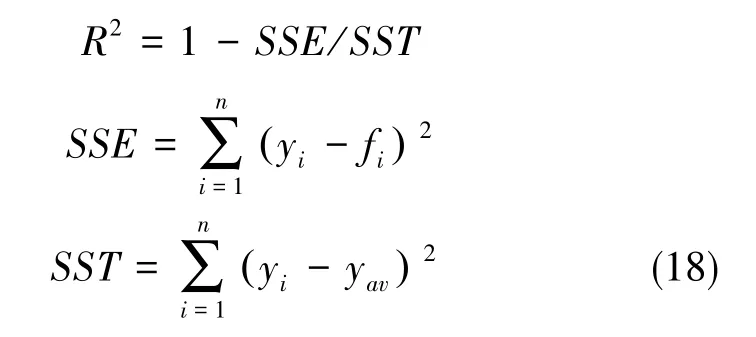
式中，SSE是殘差平方和，SST是總平方和，yi是量測數據，fi是模型預測數據，yav是yi的平均值。

采用最小二乘方法，分別使用傳統模型、改進模型對飛行數據進行擬合，通過擬合優度指標、時域曲線對其進行對比。將擬合后的改進模型與傳統模型分別與觀測數據集進行對比，可以計算擬合優度R2。擬合優度越接近于1，表示模型與數據集的匹配程度越高，所建立的模型精度越高。在試驗中，通過上下升降試驗來對比升力模型的擬合優度，通過側飛、轉動試驗對比側力模型的擬合優度，通過航向運動來對比扭矩模型的擬合優度，通過橫滾運動來對比橫滾力矩的擬合優度，通過俯仰運動來對比俯仰力矩的擬合優度。擬合優度的對比情況如表3所示，兩種模型擬合結果的時域曲線如圖3～圖10所示。其中，在加速度擬合曲線圖中，參考曲線數據為加速度計輸出；在角速度擬合曲線圖中，參考曲線數據為陀螺輸出微分。

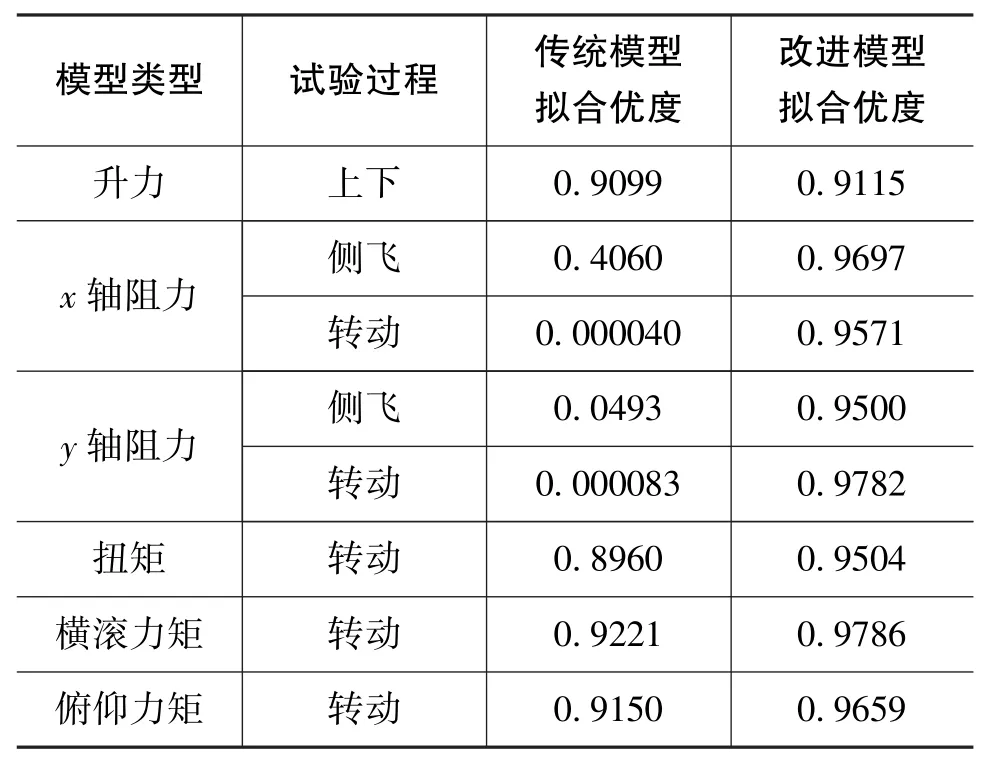
表3 兩種模型的擬合優度對比Table 3 Comparison of goodness of fit between the two models

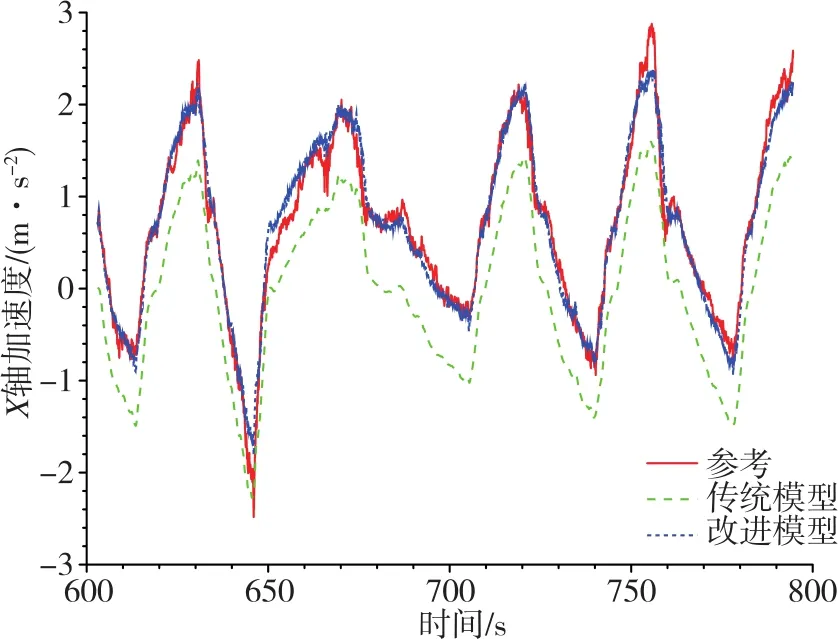
圖3 側飛試驗下X軸加速度擬合結果對比圖Fig.3 Comparison of X-axis acceleration fitting results in lateral flight test

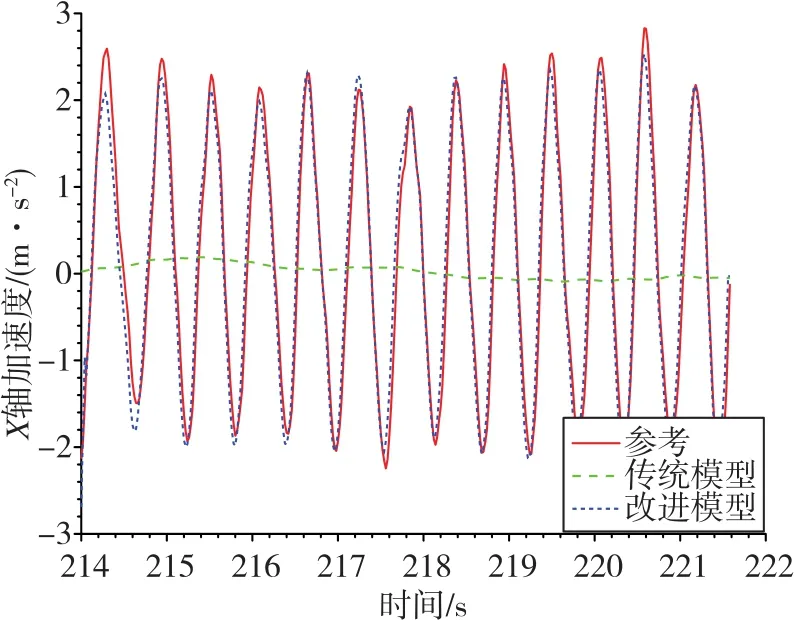
圖4 轉動試驗下X軸加速度擬合結果對比圖Fig.4 Comparison of X-axis acceleration fitting results in rolling test

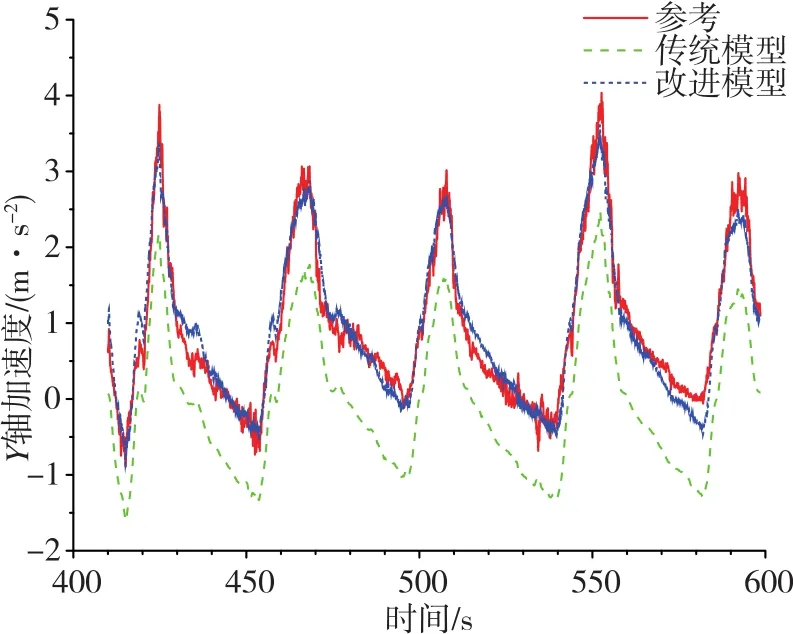
圖5 側飛試驗下Y軸加速度擬合結果對比圖Fig.5 Comparison of Y-axis acceleration fitting results in lateral flight test

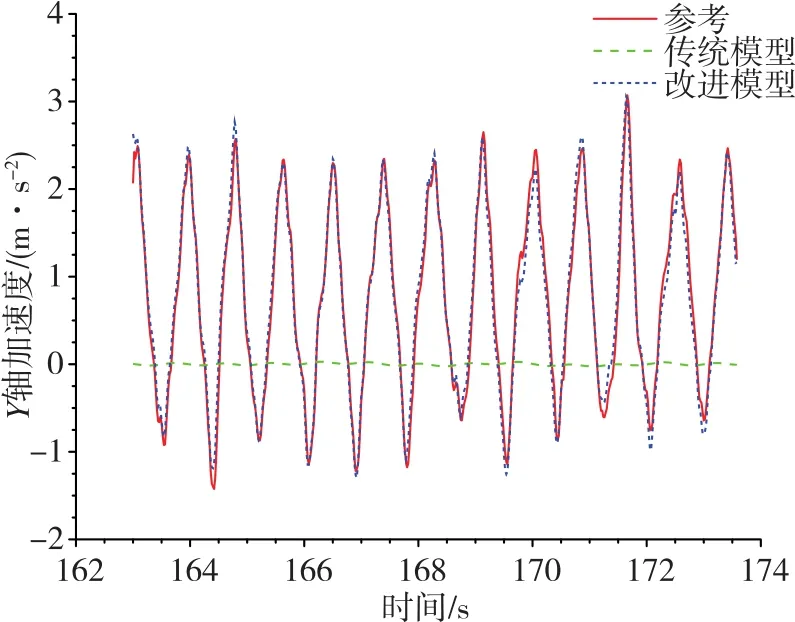
圖6 轉動試驗下Y軸加速度擬合結果對比圖Fig.6 Comparison of Y-axis acceleration fitting results in rolling test

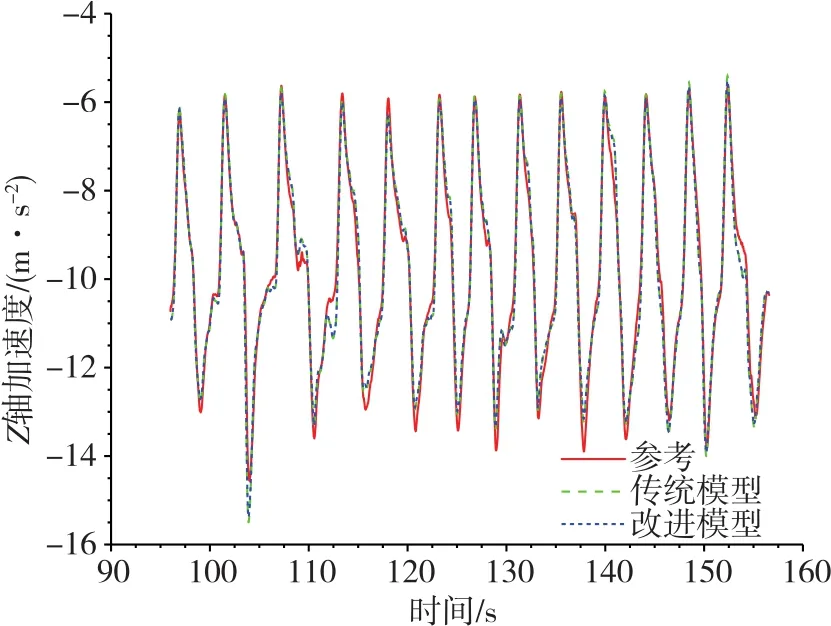
圖7 Z軸加速度擬合結果對比圖Fig.7 Comparison of Z-axis acceleration fitting results

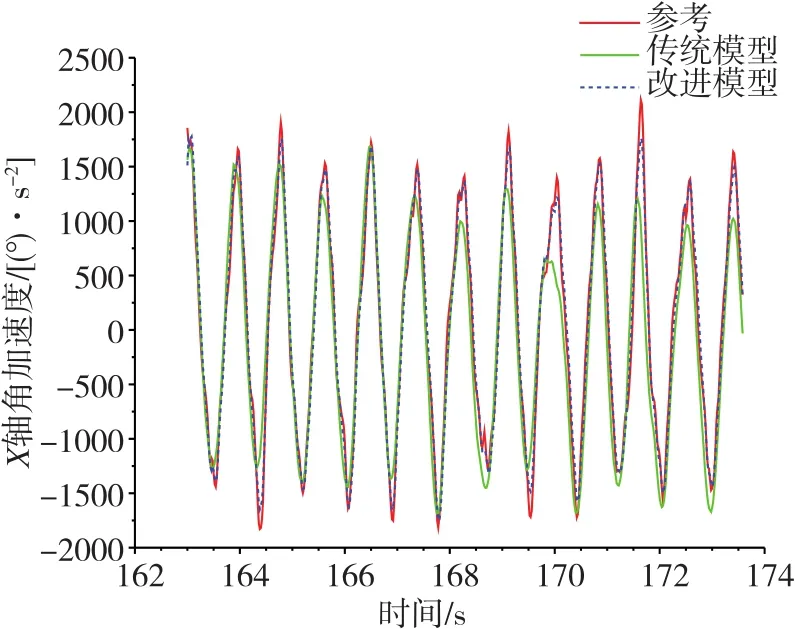
圖8 X軸角加速度擬合結果對比圖Fig.8 Comparison of X-axis angular acceleration fitting results

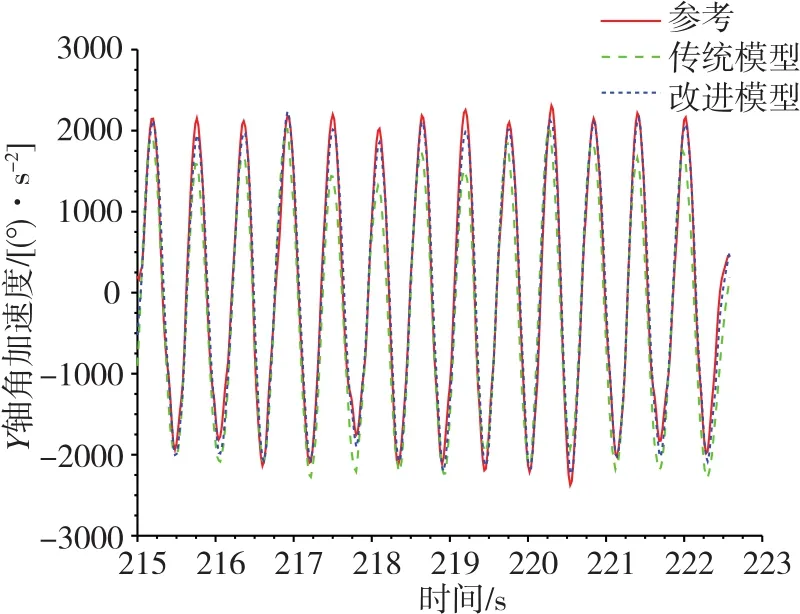
圖9 Y軸角加速度擬合結果對比圖Fig.9 Comparison of Y-axis angular acceleration fitting results

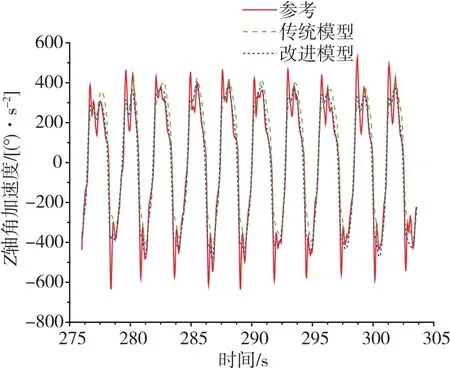
圖10 Z軸角加速度擬合結果對比圖Fig.10 Comparison of Z-axis angular acceleration fitting result

通過將擬合優度、時域曲線進行對比，可以看出：

1）對于升力、阻力、扭矩、橫滾力矩、俯仰力矩而言，其改進的動力學模型擬合優度優于傳統模型，表明改進的動力學模型與觀測的數據集擬合優度更接近于1，精度更高。

2）通過觀察圖3～圖6可以看出，對于阻力模型，在側飛狀態下，零偏項的引入較好地補償了其偏置誤差；在轉動狀態下，傳統模型呈現出了較大誤差，而改進模型與試驗結果較為符合。

3）通過圖7可以看出，改進的升力模型與傳統升力模型在時域上的擬合效果基本一致，與試驗結果均具有較高的重合性。

4）通過圖8～圖10可以看出，對于橫滾力矩、俯仰力矩及扭矩而言，改進模型與試驗結果的一致性均優于傳統模型。

3 結論

本文提出了一種改進的四旋翼飛行器動力學模型，在側飛、旋轉等機動條件下對傳統模型進行了完善：對于阻力，引入了與轉動相關的切向力；對于扭矩，引入了轉動時由阻力帶來的阻力矩；對于橫滾力矩、俯仰力矩，引入了轉動時由切向力引起的力矩項。飛行試驗表明，當四旋翼飛行器執行機動飛行時，改進的動力學模型比傳統的動力學模型具有更高的精度。