基于趨勢和跳躍成分分析方法的太河流域降水量序列研究
,,,,
(山東農業大學水利土木工程學院,山東泰安271000)
受流域氣候因素、下墊面因素以及人類活動因素的影響,降水量等水文時間序列具有隨機性、非線性、多時間尺度變化等復雜的特性[1],因而對于準確的掌握其變化規律并做出合理的預測是眾多研究的困擾。目前,學界對于水文時間序列的研究有序列相關性分析方法、水文頻率分析方法、模糊分析方法等科學的方法[2-17],但較多學者仍然通過序列相關性分析方法進行研究。該方法基于水文時間序列的平穩性假設,是一種研究序列變化趨勢和規律并對未來的情況進行判斷和預測的有效的研究方法。蔡繼等曾在相關研究中[4]運用該方法對深圳水庫的降水量序列進行了研究,結果表明深圳水庫年和汛期降水量呈增加趨勢且存在6、10、17 a的主周期,非汛期降水量呈微弱減少趨勢;袁滿等在相關研究中[5]運用該方法對沱江流域三皇廟站1941—2008年平均徑流序列進行研究,結果表明顯著突變點出現在2001年。由此可見該方法具有科學性、有效性。本文采用序列相關性分析方法對太河流域的降水量序列進行研究。
1 研究區概況
本文選取太河流域為研究區。太河流域位于山東省淄博市淄川區,東西部地勢較高,中部地勢較低,南部是東西走向的淄博冠魯山。流域面積約780 km2,長度約40.5 km,寬度約19.3 km,干流長度約61.1 km。
太河流域屬于暖溫帶半濕潤季風性氣候,春季多風,夏季多雨,秋季多旱,冬季少雪,具有春旱、夏澇、晚秋又旱的氣候特點。流域多年平均降水量約697.2 mm,受氣候與地形影響,流域降水量時空分布不均,季節性變化明顯,汛期降雨約占全年總降水量的73.5%,且雨季主要集中在7—8月份,大暴雨洪水發生概率較大[18-19]。流域內設有太河水庫、鎮后、郝峪等水文站,設有田莊、峨莊、李家莊、郭莊、趙莊、中郝峪、燕峪山頂、夏莊、南博山、南邢、石馬等雨量站,其中,田莊、趙莊雨量站位于流域內太河干流上,峨莊、郭莊雨量站位于太河二級支流上,其余雨量站皆位于太河三、四級支流上,見圖1。
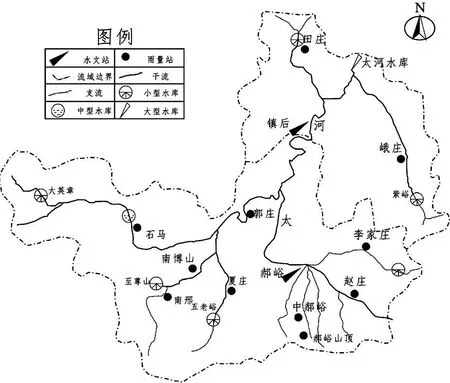
圖1 太河流域
2 理論與方法
水文時間序列是在水文要素隨時間變化過程中記錄產生的,降水量就是一種典型的水文時間序列。水文時間序列用符號Xt表示,其線性表示方法為:
Xt=Nt+Pt+St
(1)
式中Nt——水文序列的非周期成分(含趨勢、跳躍、突變成分);Pt——水文序列的周期成分(含簡單周期、復合周期及近似周期);St——隨機成分(含平穩、非平穩狀態)。其中,趨勢成分多指水文時間序列在較長的一段時期內具有一定的規則的變化,而跳躍成分多指水文時間序列從一種狀態急劇變化到另一種狀態的形式[20]。
2.1 趨勢成分分析
對水文時間序列的趨勢成分進行分析時,先對序列趨勢成分的存在性進行識別,若序列存在趨勢成分,則須對趨勢成分的顯著性進行檢驗;否則,無須進行顯著性檢驗。
2.1.1滑動平均法識別趨勢成分[20]
設有某水文序列x1,x2,x3,……,xn,對該序列的前期值和后期值取平均,得到新的序列yt,使得原序列光滑化,其相應的數學表達式為:
(2)
若序列中存在趨勢成分,選定k值,利用yt即可將趨勢清晰地顯示出來。
2.1.2Kendall秩次相關法檢驗顯著性[21]
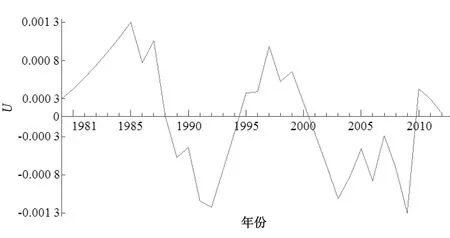
設有某水文序列x1,x2,x3,……,xn,確定序列中所有對偶值(xi,xj)(j>i)中xi 假設原序列無趨勢(H0),給定顯著性水平α,將計算求得的U值與Uα/2值進行比較,若U 對水文時間序列的跳躍成分進行分析時,先對序列跳躍成分的存在性進行識別,即識別序列有無突變點,若序列存在突變點,則須對突變點的顯著性進行檢驗;否則,無須進行顯著性檢驗。 2.2.1有序聚類法識別突變點[22] 設有某水文序列x1,x2,x3,……,xn,假設該序列的突變點為τ,構造目標函數: (3) 其中,Vτ、Vn-τ為突變點前后兩部分的離差平方和。當S取極小值時對應的τ即為突變點。 2.2.2滑動游程法檢驗顯著性[23] 突變點τ確定后,將水文序列x1,x2,x3,……,xn突變點τ前后兩部分分別用不同的字母表示,將原序列值從小到大排序并用相應的符號代替,統計連續出現相同字母序列的個數即游程記為k,前面部分的序列個數為n1,后面部分的序列個數為n2,構造如下統計量: (4) 給定顯著性水平α,將計算求得的U值與Uα/2值進行比較,若U 選取太河流域內太河水庫、鎮后、郝峪3處水文站以及田莊、峨莊、李家莊、南邢、石馬5處雨量站1979—2012年共計34 a實測降水量資料。 分別選用郝峪和李家莊2個站為代表站、石馬和峨莊為其相應的鄰近站進行可靠性分析。由以上2個站的逐年降水量相關性分析可以判斷兩個代表站與相應的鄰近站逐年降水量的差值均較小,因此該流域降水量資料的可靠性較好;采用單累計模比過程線法分析降雨資料的一致性,郝峪、李家莊2個代表站的逐年降水量模比系數過程線的總趨勢均呈單一直線關系,相關系數分別為0.9944、0.9973,相關性較好,因此該流域的降水量資料的一致性較好;采用差積曲線法、累計平均值模比系數過程線法、長短系列相對誤差分析法求得逐年降水量資料的代表期和穩定期為34 a。綜上所述,太河流域1979—2012年降水量資料的可靠性、一致性與代表性均可以保證。 借助GIS系統對實測的8個站的年降水量資料采用泰森多邊形法得到太河流域的年降水量資料序列。對該序列進行趨勢和跳躍成分分析。該序列過程線見圖2。 圖2 太河流域1979—2012年逐年降水量過程線 由圖2,太河流域1979—2012年的降水量序列中,1989年出現降水量的最小值為252.4 mm,1990年出現降水量的最大值為808.1 mm。該水文時間序列的最大波動幅度出現在1989—1990年之間,極差為555.7 mm。從過程線的整體角度來看,該水文時間序列整體趨勢不明顯且于1989—2006年之間出現較為明顯的波動,僅通過過程線無法科學合理的確定該序列的具體組成成分,遂使用序列相關性分析方法對該序列的趨勢和跳躍成分進行識別和顯著性檢驗。 3.2.1滑動平均法識別趨勢成分 對太河流域該水文時間序列使用滑動平均法進行趨勢擬合,采用滑動平均法得到結果見圖3。圖3中的滑動平均過程線顯示,太河流域的降雨量在1987—1997年、2002—2007年出現較明顯的波動,但在2007—2012年呈現較為平穩的上升趨勢;總的來看,該水文時間序列具有上升的趨勢,綜合趨勢線走勢判斷該序列具有上升趨勢。 圖3 滑動平均法回歸趨勢線 3.2.2Kendall秩次相關法檢驗顯著性 用Kendall秩次相關檢驗法對該水文時間序列的上升趨勢進行趨勢成分顯著性檢驗。取顯著性水平α=5%,假設原序列上升趨勢成分不顯著,計算得U=2.179,由顯著性水平α=5%查正態分布表得Uα/2=1.96。故U>Uα/2,則拒絕原假設,該序列上升趨勢具有顯著性。 3.3.1有序聚類法識別突變點 對該水文時間序列采用有序聚類法對序列中的突變點進行識別,經處理得到有序聚類法統計曲線見圖4。由圖4,該水文時間序列的有序聚類法目標函數S值在1996—2005年出現較明顯的波動,且波動幅度遠大于整體的平均波動幅度,但在2005— 圖4 有序聚類法統計曲線 2011年呈現較平穩的波動;綜合整體來看,S值在2002年有S=Smin,則突變點出現在2002年。 3.3.2滑動游程法檢驗顯著性 用滑動游程法對序列的跳躍成分進行顯著性檢驗。經處理得到滑動游程統計曲線見圖5。 圖5 滑動游程法統計曲線 由圖5,該水文時間序列的滑動游程法統計量U值在1985年有U=Umax=0.0013,在2009年有U=Umin=-0.0013即U值均滿足-0.0013 本次研究表明,太河流域1979—2012年降水量序列具有顯著上升的趨勢成分與不顯著的跳躍成分。綜合考慮太河流域氣候因素、地質因素以及人為因素等其他因素的影響,分析該水文時間序列的趨勢和跳躍成分的成因分析如下。 a) 自20世紀末,全球氣候變暖現象日趨明顯,由其引起的冰川消融、海平面上升、降水量增多等將進一步導致洪、澇、旱等自然災害[24]。相關研究[25-26]表明,全球氣候變暖主要是通過夏季風影響我國的降雨分布。全球溫度升高,引起亞洲東部地區夏季風強度增大,導致海陸溫差加大,使夏季風邊界向北向內陸伸展,使得中國受影響地區降水量增多。1979—2012年,隨著全球經濟的不斷發展,全球氣候變暖趨勢不斷加強,太河流域受氣候變暖因素的影響,降水量整體呈現上升的趨勢。 b) 太河水庫是太河流域內的一座大型水庫,較大的庫區面積對于氣候必定產生一定的調節作用,進而對降雨的產生具有一定的影響。 c) 跳躍突變點的出現多與水文時間序列極值點的出現有關,受水文時間序列極值預報精度普遍較差的影響[27],其誘發的自然災害越來越嚴重。據有關資料[28],2002年山東省全年平均降水量比歷年偏少,全省出現罕見的四季連旱現象,旱災影響范圍較大,全省因干旱造成的直接經濟損失達260億元,其中,淄博市即太河流域所處地級市春旱、夏旱、秋旱受災耕地面積分別占全部耕地面積的66%、83%、61%,受災害影響較大,因而出現跳躍突變點。 a) 在未來的時期,太河流域的年降水量具有較大的概率出現逐年上升的趨勢。降水量的逐年增加,使得地表徑流量逐年增加,對地表的沖刷作用也越明顯[29],故太河流域的下墊面條件會受到一定程度的破壞。 b) 降水量的增加,使得太河流域的水資源量有所增加。當地可以通過太河水庫對這部分水資源加以調節,實現有效利用,更好地為農工業發展服務。從而可以有效地緩解由于社會發展、人口增長帶來的水資源短缺問題,實現水資源的供需平衡。 c) 受自然因素與人為因素的影響,對水文時間序列的預測具有一定的不確定影響。基于此,盡管在2002年太河流域出現了特枯水年現象,但未來太河流域僅有一定的概率出現枯水年現象。2.2 跳躍成分分析
3 數據與分析
3.1 資料的三性審查
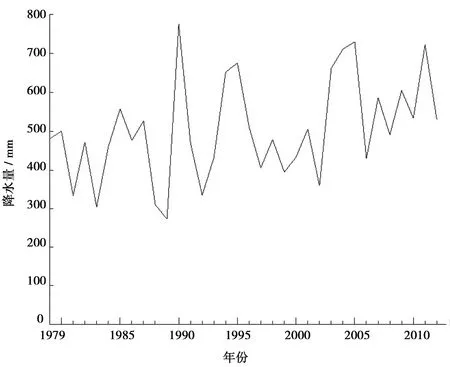
3.2 趨勢成分分析
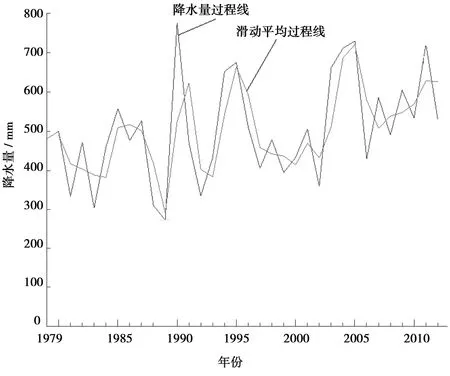
3.3 跳躍成分分析
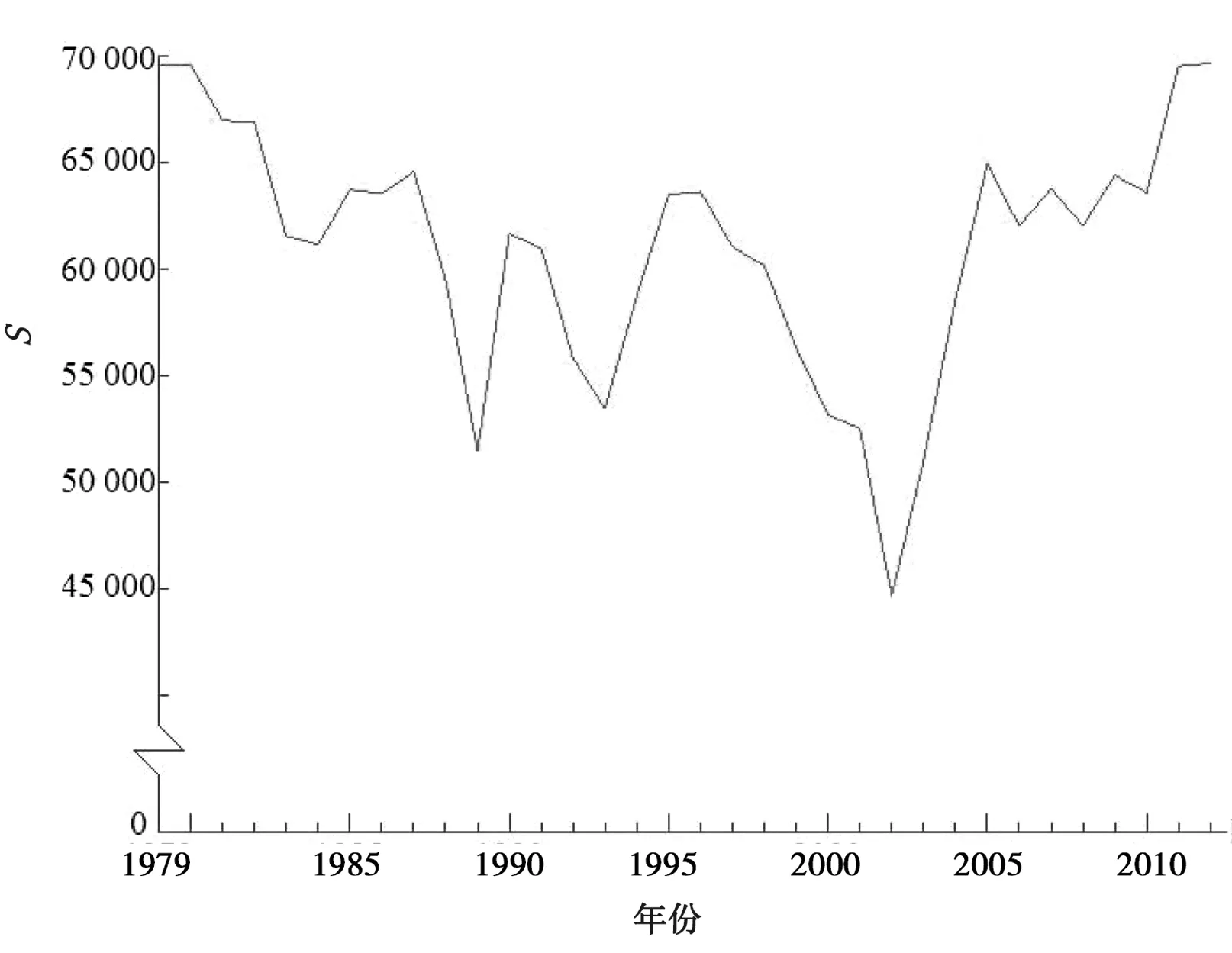
3.4 結果分析
4 結論

