電動汽車參與風電場輸出功率波動平抑方法研究

陳宇，彭瀟，丁婧，王亞洲，邵敬平

?

電動汽車參與風電場輸出功率波動平抑方法研究

陳宇1，彭瀟2，丁婧3，王亞洲1，邵敬平1

（1．湖北華電西塞山發電有限公司，湖北省 黃石市 435001； 2．國網湖北省電力有限公司荊州市荊州區供電公司，湖北省 荊州市 434100； 3．國網湖北省電力有限公司鄂州市鄂城區供電公司，湖北省 鄂州市 436000）

由于風電固有的隨機性與間歇性，使得風電場輸出功率往往具有較大的波動。然而考慮到儲能裝置的昂貴成本，單獨為風電場配置儲能裝置不利于其經濟運行。為此，文中針對考慮電動汽車參與的風電場輸出功率波動平抑方法進行了研究。根據國家標準中風電“有功功率變化”的要求，通過爬坡率概念來描述風電場輸出功率變化率。采用魯棒優化的方法處理風電出力的不確定性，建立風電機組和電動汽車協調控制的雙層優化模型：上層模型決策者是風電場，以風電場售電收益最大化為目標函數；下層模型決策者是電動汽車車主，以電動汽車電費支出成本最小化為目標函數。通過線性規劃對偶定理和Karush-KuhnTucker(KKT)最優性條件將此魯棒優化模型轉化為混合整數線性規劃問題進行求解。最后，通過仿真結果驗證了所提模型和方法的有效性。

風電場；電動汽車；功率波動；魯棒優化；雙層優化

0 引言

隨著全球環境問題日益嚴重，世界各國對清潔能源、可再生能源發電的關注度日益提高。在各種可再生能源領域中，風能作為清潔能源儲量極為豐富[1-2]。然而，風能隨天氣條件的變化很大，具有隨機性與間歇性，由于這種不確定性和波動性，使得風電場的輸出功率往往具有很大的波動，嚴重影響電網的安全性與穩定性[3-4]。因此，平滑風電輸出功率曲線是風電發展道路上一個必須解決的問題。

電池儲能系統(battery energy storage system，BESS)具有快速響應特性，能有效平抑風電場輸出功率的波動，是緩解電力系統調頻壓力的有效措施。儲能在可再生能源并網中扮演了一個很重要的角色，如提高電能質量、限制電壓波動、減少系統運行成本[5-6]。文獻[7]提出一種儲能容量最優配置的方法，該方法以平滑時間常數-合成輸出標準變差特性作為風電功率波動平抑效果的評價指標，進而通過成本性能比計算出風電場的最優儲能配置。文獻[8]基于雙層電容器和鉛酸電池儲能的等效電路進行數學建模，解決分布式可再生能源中風電引起的功率波動問題。文獻[9]提出一種儲能最優運行策略方法，該方法基于頻譜分析確定混合儲能系統(hybrid energy storage system，HESS)容量的方法，充分利用了超級電容和蓄電池的優勢互補，建立以利潤最大為目標的機會約束規劃儲能運行策略，結合蒙特卡羅算法進行求解，確定儲能的最優運行。文獻[10-11]提出蓄電池充放電控制策略，從而提高儲能設備的使用壽命，同時解決分布式可再生能源中風電引起的功率波動問題。文獻[12-13]通過構建釩電池的數學模型，分析釩電池的能量狀態與端電壓的變化特征，提出了相應的充放電策略，仿真結果表明改策略能有效地改善風電功率波動問題。文獻[14]提出量化風電功率輸出要求的風電功率波動特性指標，構建立了電池和超級電容相結合的復合儲能系統雙層優化配置模型。

在風電功率輸出要求和復合儲能成本的約束條件下進行求解，所得優化配置結果使儲能系統投資成本最小。考慮到儲能價格昂貴，儲能裝置的接入會影響系統運行的經濟性，可利用風電場內部已有的儲能裝置參與風電場輸出系統功率調節。

隨著V2G(Vehicle-to-grid)技術的不斷發展[15-16]，電動汽車在實現其行駛功能的基礎上，可通過控制其充放電功率，平抑風電場輸出功率波動，達到單獨配備儲能裝置的效果。

1 風電場輸出功率波動問題描述

在電力系統中，頻率是表征電能質量的重要指標之一，保證頻率符合要求是電力系統運行調度的一項重要任務。風電出力具有較強的隨機性、波動性和反調峰性等特征。隨著風電滲透率不斷增加，風電出力變化率已成為影響電力系統頻率穩定的關鍵因素，因此，風電并網發電功率變化應當滿足電力系統安全穩定運行要求。根據《GB/T 19963—2011風電接入電力系統技術規定》對風電并網運行時輸出功率變化量的規定，建立風電場輸出功率變化率表達式[17]，如式(1)所示：

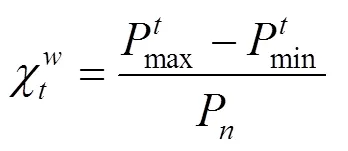
2 基于魯棒優化的風電機組與電動汽車聯合調度模型

2.1 風電出力不確定性集合

魯棒優化模型中常用盒式不確定集形式描述不確定性變量的波動范圍，但盒式決策空間過于保守，所以本文選擇解的保守度可控制的多面體不確定集合代替盒式不確定集合。為了計算方便，通常要求不確定性集合為閉凸集，一種常用的多面體不確定性集合構造方法[18]，如式(2)所示：

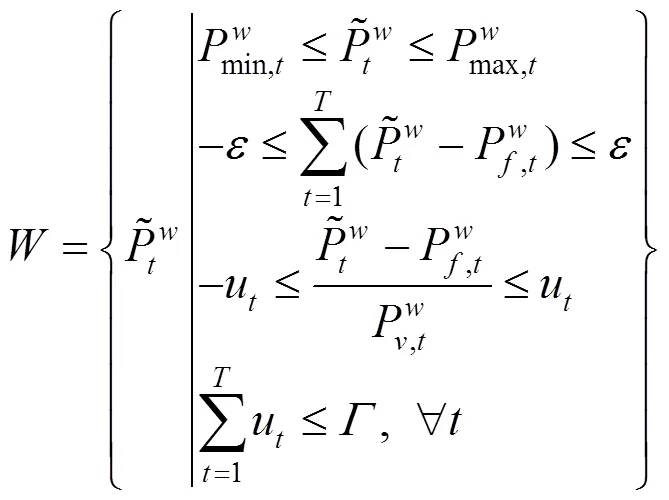
2.2 魯棒優化調度模型

以含電動汽車的風電場為研究對象，充分利用電動汽車的充放電功能應對風電輸出功率波動。以風電場售電利潤最大化和內部電動汽車用戶電費支出最小化為目標函數，建立了風電機組和電動汽車協調控制的雙層優化模型，上層模型決策者是風電場，下層模型決策者是電動汽車車主。雙層優化結構如圖1所示。

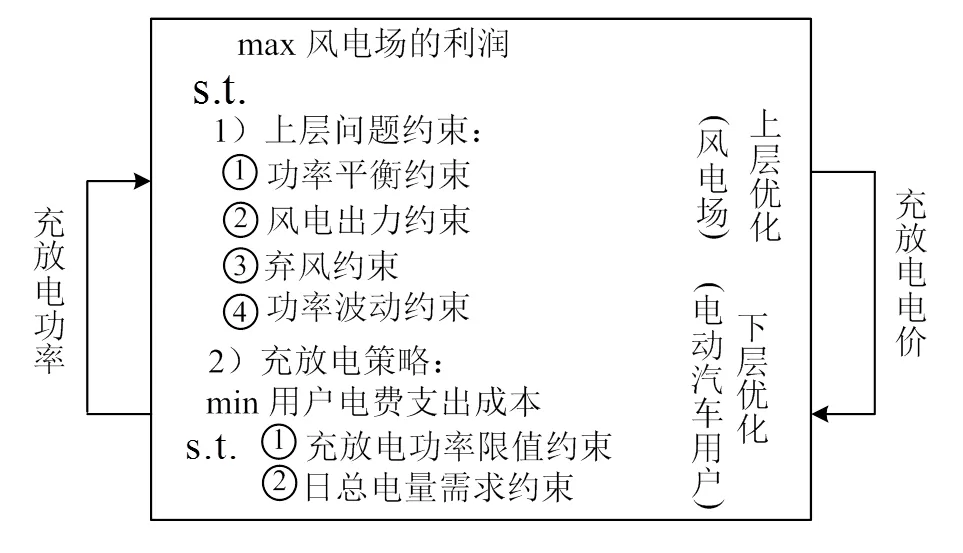
圖1 雙層優化結構示意圖

1）上層優化模型。

風電場的輸出功率優化問題如下：

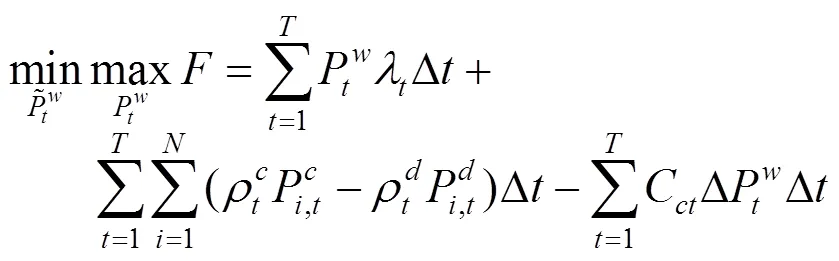
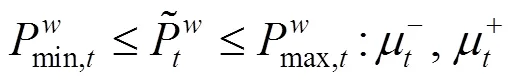
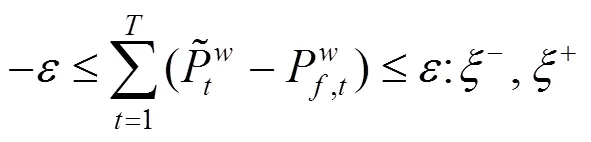
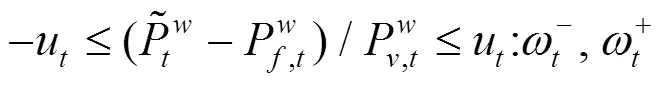
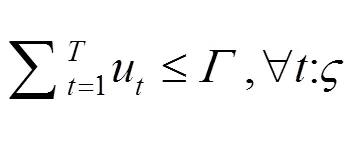
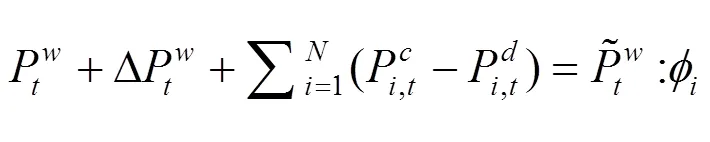
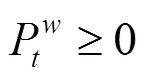
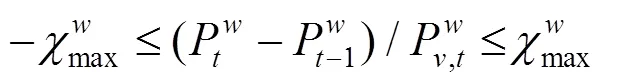
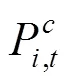
上述公式(3)—(10)中，目標函數式(3)極小化極大化風電場的收益，即考慮在最差情況下收益最大化的決策。風電場的收益由3部分組成，其中第1項代表向批發市場出售風電的收入；第2項為電動汽車用戶支付給風電場的電費收入，包括充電成本和放電補償費用；第3項為風電場的棄風成本。式(8)是有功率平衡約束。式(9)是風電運場日前投標出力上下限約束，表明風電場在日前市場的投標出力必須大于或等于0，投標為0表明該時段不參與市場發電。式(10)為風電場輸出功率波動上下限約束。

2）下層優化模型。

下層決策者電動汽車的充放電功率優化問題如下：

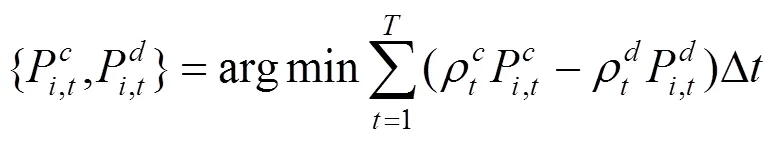
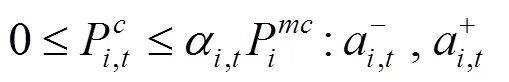
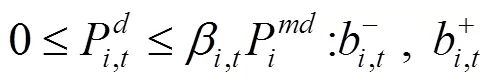
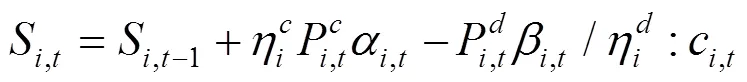
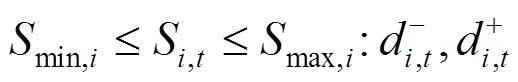
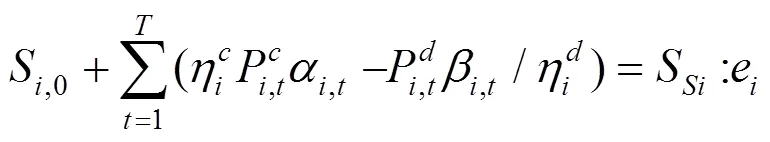
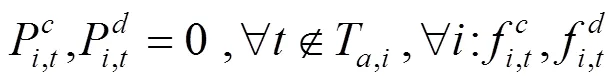
上述公式(11)—(17)中，目標函數式(11)表示在風電場給出的充放電價格下極小化自身電費支出成本；式(12)、(13)表示各輛電動汽車充放電功率上下限；式(14)、(15)為荷電狀態約束，為了減小充放電對車載電池壽命的影響，需對電池的荷電狀態加以約束；式(16)表示電動汽車用戶出行需求約束，即電動汽車作為用戶出行交通工具，在對其進行充放電控制的時候首先要考慮滿足用戶的出行需求；式(17)是電動汽車用戶充放電狀態約束，風電場只在T,i時段內對電動汽車進行充放電控制。

風電場優化問題式(3)—(10)和所有電動汽車優化問題式(11)—(17)構成了主雙層優化模型，該模型最初由Stackelberg在文獻[19]中提出，并在文獻[20]中給出了上下層模型均為線性時的求解方法。下文基于對偶理論和Karush-KuhnTucker (KKT)條件將式(3)—(10)、(11)—(17)轉化為混合整數線性規劃，從而可以采用高效商業求解器CPLEX 12.2對模求出全局最優解，即上下優化問題的均衡點。

3 魯棒優化模型的轉換及其求解

3.1 上層優化模型的對偶轉換

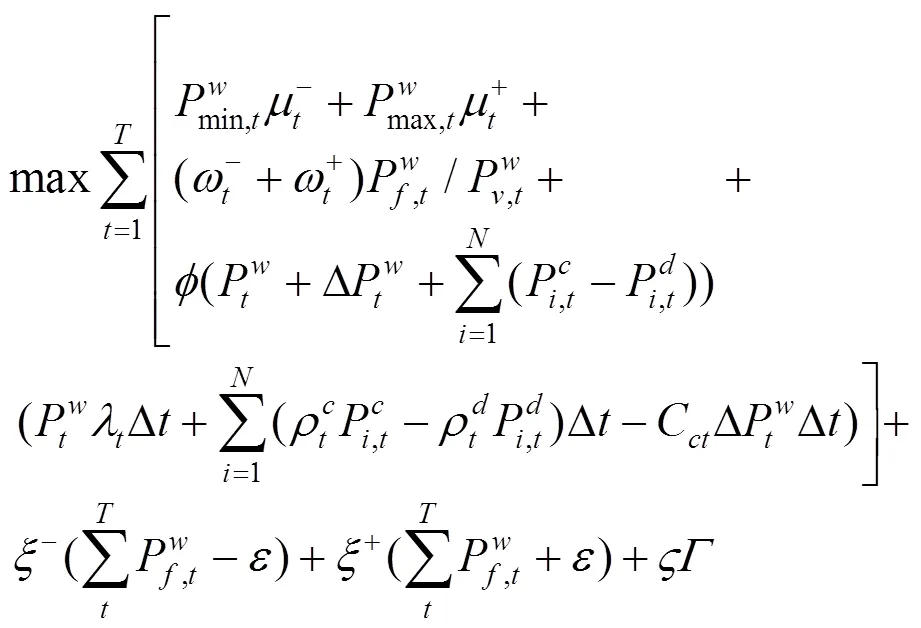
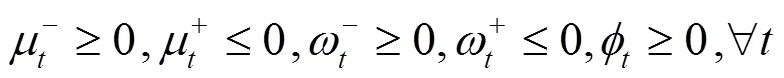
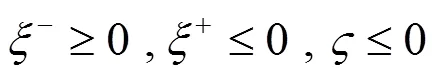
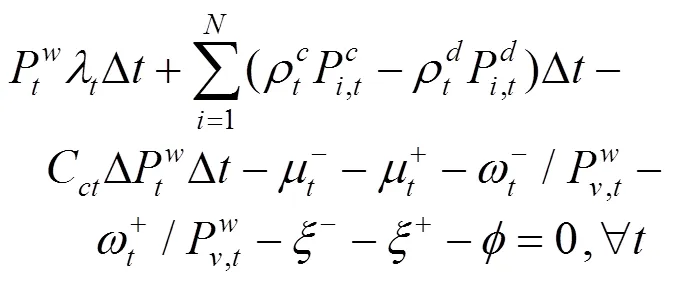
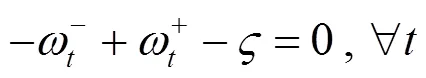
約束條件同公式(9)、(10)。

由式(18)—(22)可以看出，原上層模型經對偶轉換后變成一個線性規劃問題，從而簡化了模型的求解。

3.2 下層優化模型的KKT轉換

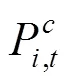
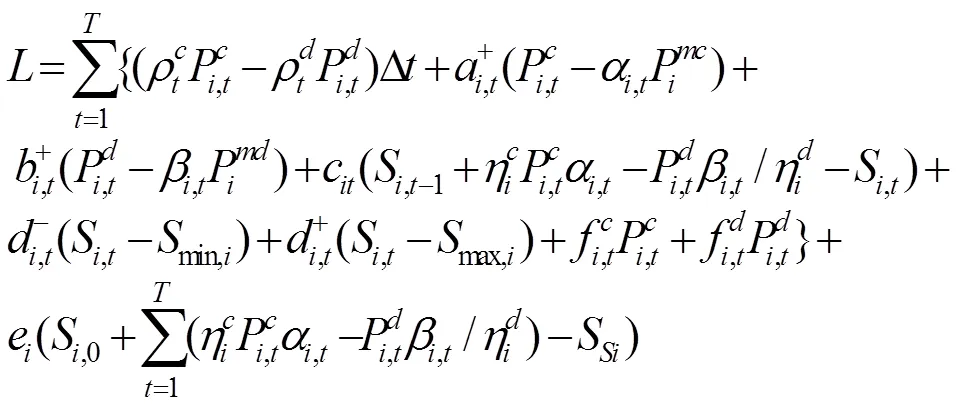
通過KKT條件將下層優化模型轉化為下列約束條件：

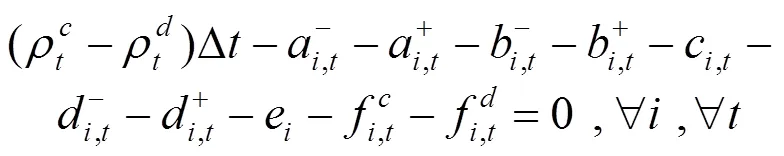
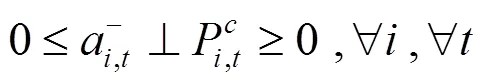
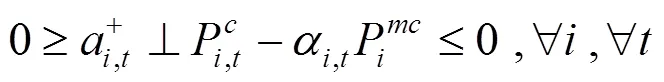
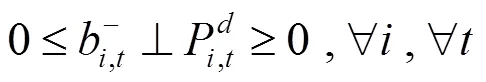
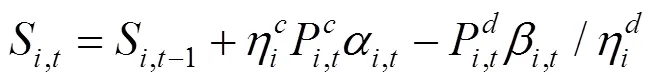
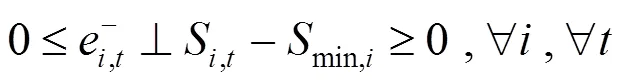
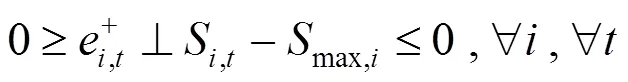
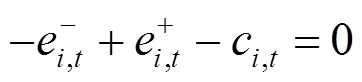
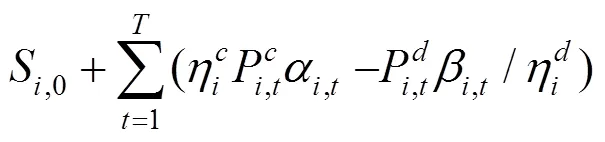
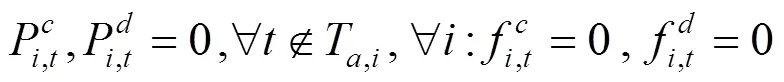
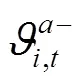
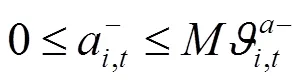
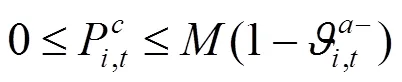
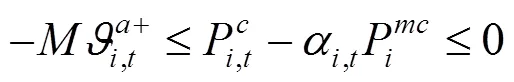
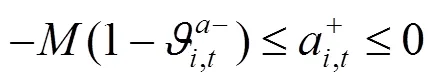
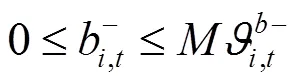
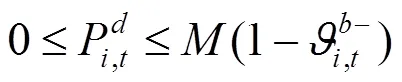
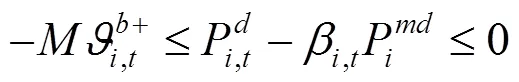
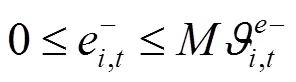
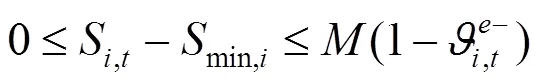
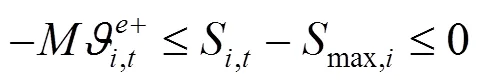
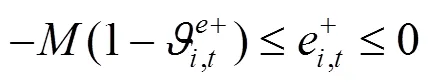
綜上所述，風電場優化調度模型可轉化為如下混合整數線性規劃：

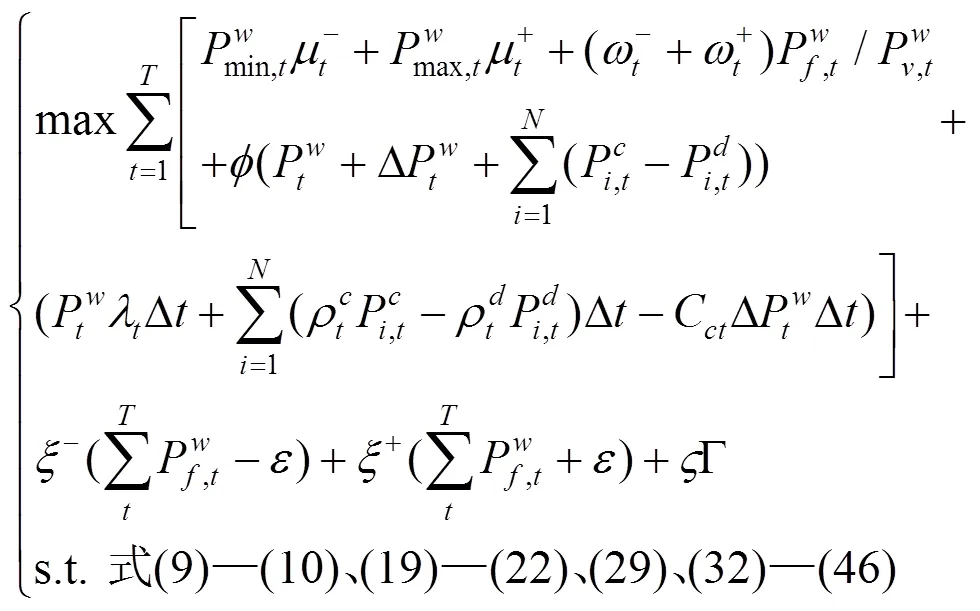
4 算例分析

4.1 上參數設置

本文研究的風電場主要包括：8臺額定功率為2 MW的風電機組，300輛電動汽車。假設風機出力服從形狀參數為2.15，尺度參數為14.99的Weibull分布，采用蒙特卡洛抽樣的方法對風電出力的隨機性進行模擬，抽樣次數為5000次，圖2給出了風電出力均值波動曲線圖。為了方便顯示計算結果，假設等值聚類后電動汽車可分為3組[22]，各組有=[90,140,70]輛電動汽車，各組電動汽車最小荷電容量均為9 kW×h，離網荷電容量均為35 kW×h，最大充放電功率均為4.5 kW，充放電效率取0.9。各組電動汽車并網充放電時間如表1所示，其中1為電動汽車接入電網時間段，0為電動汽車離網時間段。根據電動汽車行駛特性，把早出晚歸的作為第1組(工作時間06:00—20:00)，正常工作時間的作為第2組(工作時間08:00—17:00)，夜間工作時間的作為第3組(工作時間20:00—06:00)。這里設置第1組為主要類型。

按照《GB/T 19963—2011風電接入電力系統技術規定》對風電并網運行時輸出功率變化量的規定，要求裝機容量小于30MW的風電場有功功率波動應小于20%。日前市場電價、電動汽車充放電電價見表2。風電場為激勵電動汽車用戶參與風電功率調節，電動汽車的充電價格一般制定的比市場電價略低，電動汽車的放電價格一般制定的比市場電價略高。

圖2 風電出力均值

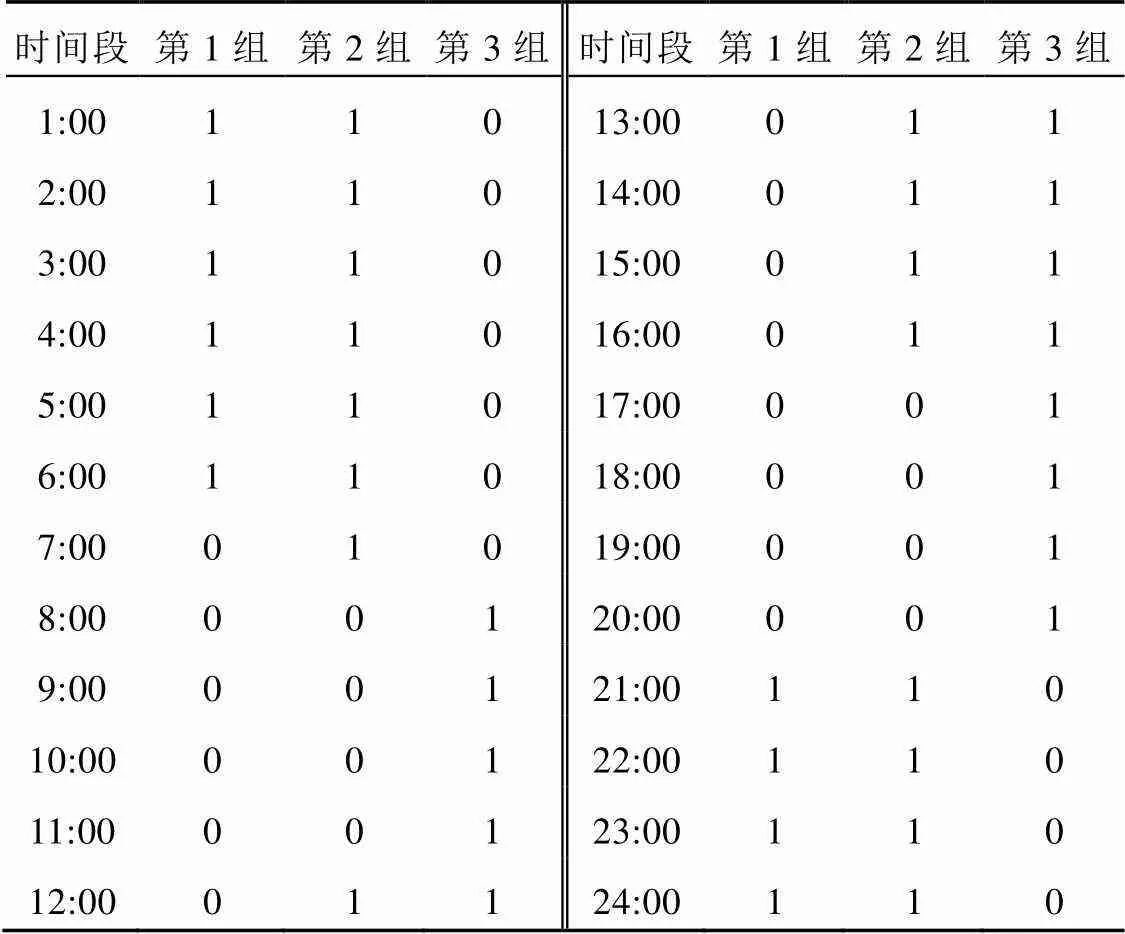
表1 不同組的電動汽車充放電時間段

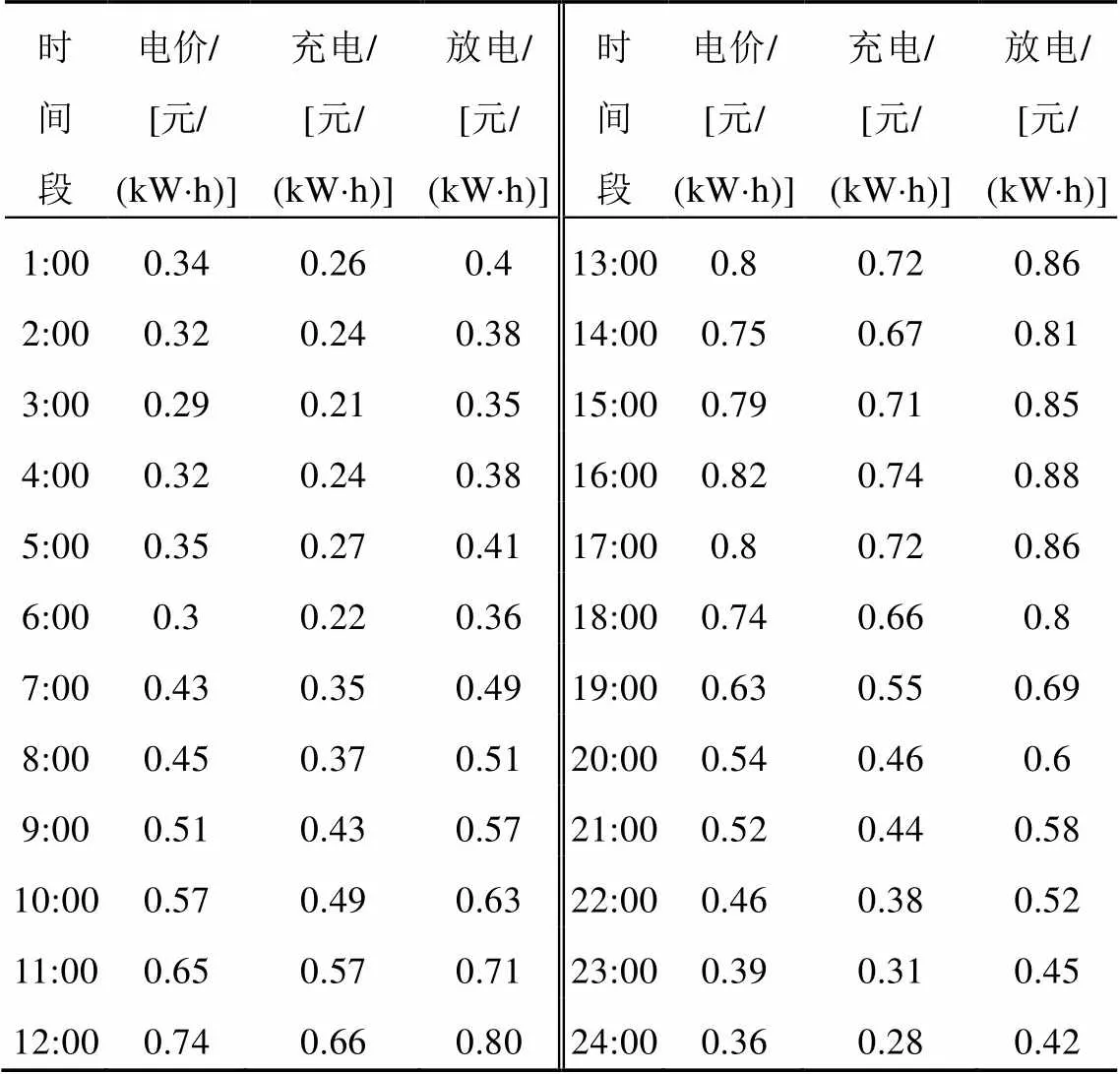
表2 日前市場電價、電動汽車充/放電電價

4.2 電動汽車配置比對優化結果的影響

在保證3組電動汽車總數量不變的前提下，改變各組中電動汽車的數量，所得優化結果見 圖3。對比分析圖3中風電場收益可以發現，在電動汽車配置比4=[90,140,70]下，風電場電收益最大，電動汽車配置比1=[0,0,300]時，風電場售電收益最小。這是因為配置比1下電動汽車主要為夜間行駛，白天并網充放電，而風電出力主要集中在夜晚，且夜間風電出力波動比較劇烈，因此配置比1下風電場晚上棄風最嚴重，相應棄風成本增加，從而導致風電場售電收益最低；配置比2、3下風電場收益比配置比1下風電場收益高，因為配置比2、3類型電動汽車主要并網充放電時間為夜晚，風電場棄風量少，能夠較好地平抑夜間風電場輸出功率波動；配置比3比配置比2類型電動汽車夜間并網充放電的時間長，所以配置比3比配置比2類型電動汽車風電場的售電收益要高；而在電動汽車配置比4下一天中各時段都有電動汽車并網充放電，且在夜晚時段電動汽車接入數量較大，能夠有效平抑風電場一天當中各時段輸出功率波動，降低了棄風成本，從而該配置比下的售電收益最大。

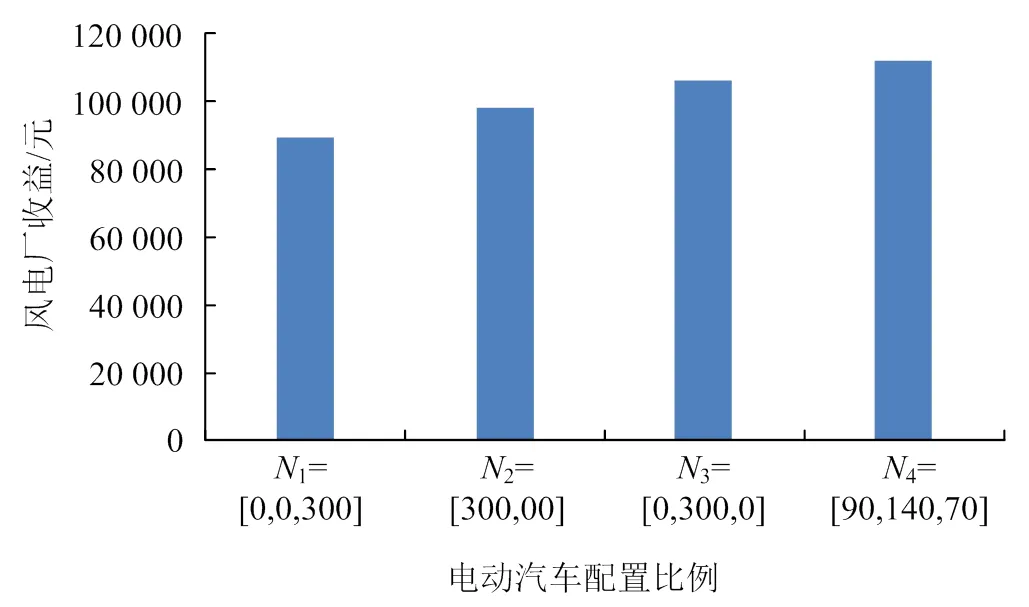
圖3 不同電動汽車配置比例下風電場售電收益

為分析電動汽車參與風電場輸出功率調節給自身帶來的收益，圖4給出了電動汽車直接從批發市場購電成本和由風電場代理其參與批發市場購電成本情況。由圖4可以看出，在各電動汽車配置比下車主向風電場購電成本均低于直接向批發市場購電成本。同時，在電動汽車配置比例為1時，直接向批發市場購電成本與向風電場購電成本的差值比較小。這是因為該配置比例下由“夜間型”電動汽車為主，該類型電動汽車主要并網時間為白天，而白天時間風電功率波動較小，電動汽車參與風電場輸出功率調節的效果也較差，因此獲得的充放電補償也相對較低，所以充電成本與直接從批發市場充電成本相差不大。然而，直接從批發市場購電成本仍是高于車主的充電成本，所以，車主參與風電場的功率調節仍是受益的。

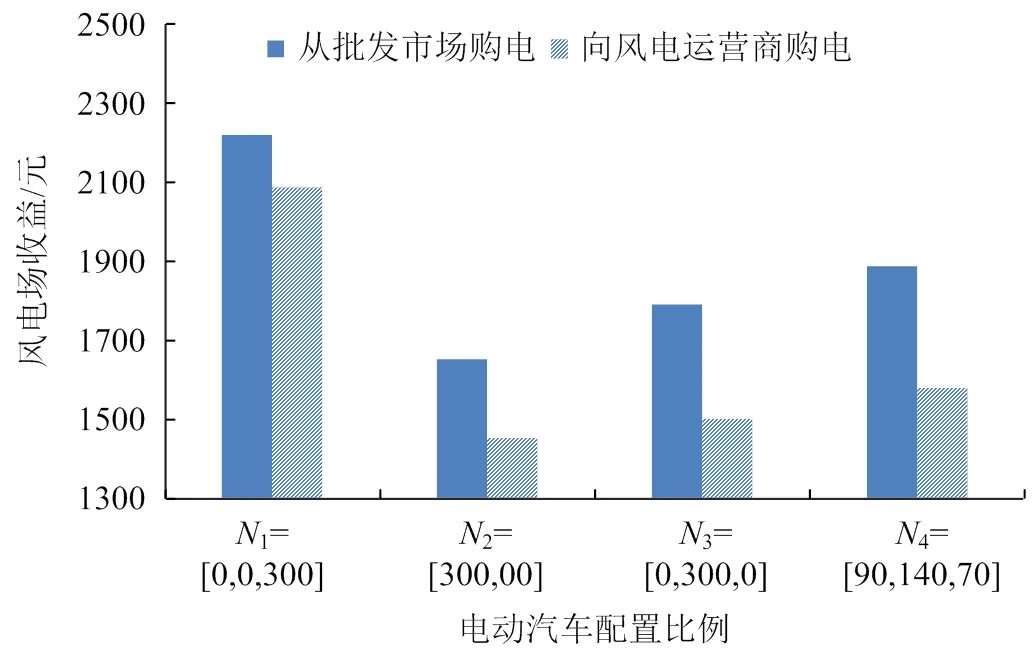
圖4 不同電動汽車配置比例下充電成本對比

4.3 魯棒控制系數對優化結果的影響

本文定義棄風改善率以反映電動汽車接入后的棄風改善情況，其具體表達式為

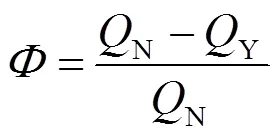
式中：N為電動汽車接入前調度周期內風電場棄風總量；Y為電動汽車接入后調度周期內風電場棄風總量。該指標描述了電動汽車接入后增加的風電并網總量占初始棄風總量的比例，該值越大表示電動汽車改善棄風效果越為顯著。

圖5給出了魯棒控制系數在0~24范圍內不同電動汽車配置比下的棄風改善率。由圖5可以看出，當電動汽車配置比例一定時，隨著魯棒控制系數的增加，棄風改善率呈減小趨勢。這是因為魯棒控制系數取值越大，表明風電功率波動越劇烈，由于電動汽車調節能力有限，因此越惡劣情況下風電場棄風現象越嚴重，對應的棄風改善率降低。雖然魯棒控制系數取值越小，風電場通過電動汽車調節輸出功率波動效果越好，但在取值較小下得到調度方案將使風電場在最惡劣情況發生時面臨的風險變大。這是因為取值越小，風電場的經濟性固然越好，但是魯棒性較差，不利于系統安全可靠運行。因此，風電場需根據實際運行情況合理的選擇魯棒控制系數，從而實現最終決策的經濟性與安全性平衡。

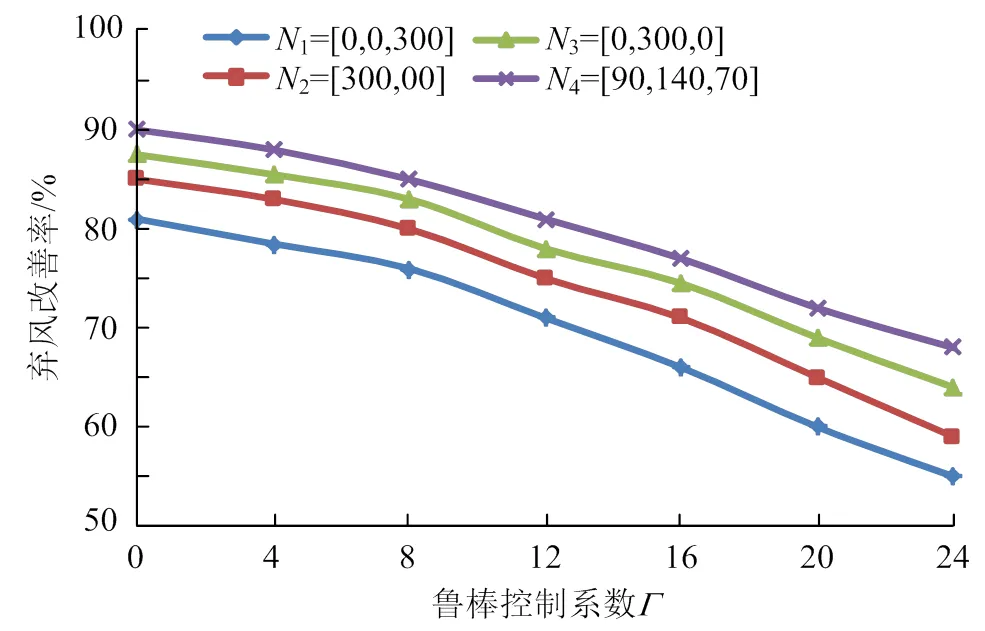
圖5 不同魯棒控制系數下棄風改善情況對比

5 結論

以含電動汽車的風電場為研究對象，分析了電動汽車參與調度對風電場并網功率的影響。結論如下：

1）由于風電出力具有較強的隨機性、波動性，其概率分布難以被準確刻畫，文中基于魯棒優化的方法處理風電出力的不確定性，即將不確定的風電出力限定在一個確定的區間內，并引入魯棒控制系數來調節不確定集合的區間大小，從而得到具有不同保守程度的優化決策方案。

2）構建的風電機組和電動汽車協調控制的雙層優化模型：上層優化模型決策者是風電場，以風電場收益最大化為目標函數；下層優化模型決策者是電動汽車車主，以電動汽車電費支出成本最小化為目標函數，綜合考慮了電動汽車用戶出行需求和電費支出滿意度。另外，還進一步通過線性規劃對偶定理和KKT最優性條件將此魯棒優化模型轉化為混合整數線性規劃問題進行 求解。

3）算例分析結果表明，將電動汽車作為可移動的儲能裝置，用來平抑風電出力波動，可有效降低棄風量，緩解風電出力不確定性對電網安全運行的影響；風電場可根據自身風險偏好，調整魯棒控制系數，從而得到兼顧經濟性和安全性的決策方案。

4）應用電動汽車平抑風電場輸出功率的波動，其目的僅僅是為了滿足系統的調頻要求，在實際應用中需要將風機電動汽車聯合的輸出功率作為負的負荷，加到原始負荷中去，綜合風電功率和負荷功率的波動趨勢，得到最優的調度方案，因此，作者將在后續的工作中對這方面內容作進一步研究。

[1] 申寬育．中國風能資源與風力發電[J]．西北水電，2010(1)：76-81．

[2] 韋東遠．世界風電產業發展趨勢[J]．東北電力技術，2009(3)：37-40．

[3] 薛禹勝，雷興，薛峰，等．關于風電不確定性對電力系統影響的評論[J]．中國電機工程學報，2014，34(29)：5029-5040．

[4] 劉文穎，文晶，謝昶，等．考慮風電消納的電力系統源荷協調多目標優化方法[J]．中國電機工程學報，2015，35(5)：1079-1088．

[5] Eorgilakis Pavlos S．Technical challenges associated with the integration of wind power into power systems[J]．Renewable and Sustainable Energy Reviews，2008(12)：852-863．

[6] Yang T C，Yue D，Xin H H．On embedded energy storage for high penetration of wind power[J]．Wind Engineering，2008(32)：223-242．

[7] 楊水麗，惠東，李建林，等．適用于風電場的最佳電池容量選取的方法[J]．電力建設，2010，31(9)：1-4．

[8] Yoshida Y，Wu Guohong，Minakawa T．Mitigating fluctuation of wind turbine power generation system by introduction of electrical energy storage with combined use of EDLC and lead acid storage battery [C]//International Conference on Power System Technology，IEEE，2010：1-7．

[9] 陳厚合，杜歡歡，張儒峰，等．考慮風電不確定性的混合儲能容量優化配置及運行策略[J]．電力自動化設備，2018，38(8)：174-182．

[10] 雷珽，歐陽曾愷，李征，等．平抑風能波動的儲能電池SOC與濾波協調控制策略[J]．電力自動化設備，2015，35(7)：126-131．

[11] 顏偉，呂冰，趙霞，等．含高滲透率風電配網中電池儲能系統和開關的協調規劃[J]．電力自動化設備，2015，35(3)：6-11．

[12] 畢大強，葛寶明，王文亮，等．基于釩電池儲能系統的風電場并網功率控制[J]．電力系統自動化，2010，34(13)：72-78．

[13] Wang Wenliang，Ge Baoming，Bi Daqiang，et al．Grid-connected wind farm power control using VRB-based energy storage system[C]//IEEEEnergy Conversion Congress and Exposition，2010．

[14] 謝應昭，盧繼平，翁宗林，等．改善風電輸出功率特性的復合儲能系統優化配置[J]．電網技術，2016，40(7)：2052-2058．

[15] 孫國強，袁智，耿天翔，等．含電動汽車的虛擬電廠魯棒隨機優化調度[J]．電力系統自動化，2017，41(6)：44-49．

[16] 盧志剛，王薈敬，趙號，等．含V2G的虛擬電廠雙層逆魯棒隨機優化調度策略[J]．電網技術，2017，41(4)：1245-1252．

[17] 龐明，史儀凱，袁小慶，等．平抑風電功率波動混合儲能系統容量優化方法[J]．西北工業大學學報，2016，34(3)：493-498．

[18] Wei W，Liu F，Mei S．Energy pricing and dispatch for smart grid retailers under demand response and market price uncertainty[J]．IEEE Transactions on Smart Grid，2015，6(3)：1364-1374．

[19] Stackelberg H V．Marktform Und Gleichgewicht [M]．Vienna：Springer，1934．

[20] Anandalingam G，White D J．A solution method for the linear static Stackelberg problem using penalty functions[J]．Automatic control IEEE Transactions on，1990，35(10)：1170-1173．

[21] Fortunyamat J，Mccarl B．A repressentation and economic interpretation of a two-level programming problem[J]．Journal of the Operational Research Society，1981，32(9)：783-792．

[22] 魏韡，陳玥，劉鋒．基于主從博弈的智能小區代理商定價策略及電動汽車充電管理[J]．電網技術，2015，39(4)：939-945．

Research on the Method of Stabilizing the Power Output Fluctuation of Wind Farm by Electric Vehicles

CHEN Yu1, PENG Xiao2, DING Jing3, WANG Yazhou1, SHAO Jingping1

(1. Hubei Huadian Xisaishan Power Generation Co. LTD, Huangshi 435001, Hubei Province, China; 2. State Grid Hubei Electric Power Co., LTD, Jingzhou City Jingzhou District Power Supply Company, Jingzhou 434000, Hubei Province, China; 3. State Grid Hubei Electric Power Co., LTD, Ezhou City Echeng District Power Supply Company, Ezhou 436000, Hubei Province, China)

Owing to the inherent randomness and intermittency of wind power, the output power of wind farm tends to fluctuate greatly. However, considering the high cost of energy storage device, it is not good for the wind farm to configure energy storage device. This paper studies the fluctuation of output power fluctuation in the wind power field considering the participation of electric vehicles. Firstly, according to the requirement of the national standard of stroke, "active power change", the rate of output power of wind farm is described by the concept of climbing rate. Then, using the robust optimization method to deal with the uncertainty of wind power, wind turbines and electric cars, coordinated control of bi-level optimization model: the upper model decision makers is a wind farm, with wind farms sell electricity utility maximization as the objective function; The lower-level model decision makers are electric car owners, and the cost of electric power costs is minimized to the target function. In addition, this robust optimization model is transformed into a hybrid integer linear programming problem by using the linear programming dual theorem and Karush-Kuhn Tucker (KKT) optimality conditions. Finally, the effectiveness of the proposed model and method is verified by simulation.

wind farm; electric vehicle; power fluctuation; robust optimization; double layer optimization

10.12096/j.2096-4528.pgt.18151

2018-10-09。

陳宇(1995)，男，碩士，研究方向為電力系統繼電保護，815034513@qq.com。

陳宇

(責任編輯 楊陽)