裸裝藥艙內爆炸壓力載荷規律研究*

姚 迪 羅 剛 謝 偉 李德聰

(中國人民解放軍海軍駐426廠軍事代表室1) 大連 116012) (中國艦船研究設計中心2) 武漢 430064)

0 引 言

隨著反艦導彈高效突防及毀傷威力的大幅提升，各種高性能反艦導彈已成為水面艦船最主要的水上威脅武器[1].現代大中型水面艦船普遍采用薄殼結構，無法阻止導彈戰斗部的動能侵徹作用，因此，戰斗部可直接穿入艦船內部艙室爆炸.導彈戰斗部對艦船的毀傷作用可分為動能侵徹與艙內爆炸兩個主要毀傷過程，戰斗部動能侵徹過程主要造成艦船外板結構的局部破壞， 而艙內爆炸過程則可造成艦船結構的大面積破壞，特殊工況下可導致艦船結構總強度的喪失，因此，研究艙內爆炸載荷特性及其作用規律對艦船防護結構設計十分重要.

與開放空間不同，艦船內部相對密閉，爆炸載荷受約束環境的影響十分顯著，結構壁面承受復雜的多次反射沖擊波作用，在角隅處沖擊波會產生匯聚效應，連接部位易發生撕裂破壞；同時會產生較長時間(相對于沖擊波)作用的準靜態壓力，沖量很大，可使結構發生塑性大變形乃至發生整體破壞[2].針對密閉/半密閉空間(典型如壓力容器及坑道)裸裝藥爆炸沖擊波載荷問題，王等旺等[3-5]開展了相關研究，并提出了一系列爆炸壓力載荷幅值及持續時間的經驗計算公式.但實際艦船艙室結構特征與上述典型空間存在較大的差異，針對上述空間結構提出的這些計算公式是否適用于艦船艙室結構不得而知.此外，已有的模擬艙室內爆炸試驗表明，沖擊波在結構角隅處的匯聚效應是造成結構撕裂破壞的重要因素[6]，但目前針對典型艦船艙室結構中的沖擊波角隅匯聚效應及規律研究相對較少，針對典型艙室內的準靜態壓力的研究也不足，尚無可用于工程設計的計算公式，因此,有必要針對裸裝藥在典型艦船艙室結構內爆工況下壓力載荷問題開展研究.

本文采用非線性瞬態動力學分析軟件MSC.Dytran，針對自由場爆炸沖擊波載荷進行了計算，通過與經典經驗公式的對比，確定了計算材料模型、網格尺度及空氣域的離散方法等；在此基礎上詳細研究了1，3 kg當量TNT裸裝藥在立方體(1 m×1 m×1 m)艙室結構內爆工況下，沖擊波載荷在艙室角隅的匯聚效應與規律，以及準靜態壓力載荷幅值；最后針對典型艦船艙室結構，重點分析了爆炸沖擊波在艦船典型艙室結構內的傳播與匯聚規律，可為艦船抗爆結構設計提供有益的參考.

1 自由場爆炸沖擊波載荷數值模擬研究

1.1 經典經驗計算公式

針對自由場沖擊波超壓，主要有Henrych,Brode、Wu Chengqing、Науменко等一系列經驗計算公式[7]，孔祥韶[8]對各公式進行了比較分析，見圖1.由圖1可知，除Науменко公式外，其余公式在適用范圍內吻合程度較好；此外與其他公式相比，Henrych公式的適用范圍更廣，因此，本文選擇Henrych公式為基準，將數值模擬結果與其進行對比分析.

圖1 自由場沖擊波超壓峰值經驗公式比較

Henrchy經驗計算公式為

(1)

(2)

(3)

式中：Δpm，0.1 MPa；W為炸藥的質量，kg；R為離裝藥中心的距離，m.

1.2 有限元計算模型及參數設置

采用非線性瞬態動力學分析軟件MSC/Dytran，模擬質量分別為20 kg及50 kg的球形TNT炸藥在理想氣體中爆炸.空氣計算域為10 m×10 m×10 m，爆點位于空間域的幾何中心.單元類型為8節點立方體單元，單元尺寸約80 mm×80 mm×80 mm,節點總數為72 900，單元總數為66 924.

空氣 假設空氣為無黏性理想氣體，沖擊波的傳播為等熵絕熱過程，空氣采用γ律狀態方程確定，狀態方程參數[9]見表1.

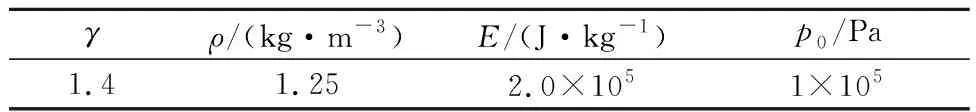
表1 空氣狀態方程參數

TNT炸藥 TNT炸藥狀態方程采用標準的JWL方程.

(4)

式中：η=ρ/ρ0(炸藥密度/空氣密度);A，B，ω，R1，R2，e為炸藥的材料常數，其中各參數見表2.

表2 TNT狀態方程參數

假定炸藥包為球形炸藥包，歐拉域采用球形有限元模型進行數值模擬.由于球形炸藥包傳播方向為一個360°的球形區域具有對稱性，為減小計算量，取15°模型為計算模型，全部采用六面體歐拉單元，將TNT裝藥處設置為坐標原點.為了避免沖擊波在邊界處產生積壓和反射，在邊界處設置為自由流出邊界.有限元模型見圖2.

圖2 球形空氣域及TNT模型圖

1.3 計算方法和計算工況

在進行有限元計算時，可采用有限體積法或歐拉網格法(ROE方法).有限體積法是Dytran軟件計算時默認的算法，在求解過程中同時滿足物質在有限體積內的質量守恒、動量守恒、能量守恒、狀態方程和本構關系，可應用于不同的初始條件.Roe方法是根據Philip Roe教授思想開發的、用于氣體和液體流動分析的計算方法，該方法基于有限元表面的所謂黎曼解.算法的具體過程相當于把問題分解成一個離散波的傳播過程，通過將局部黎曼解的原理應用在單元表面，得到了一個性能優越且穩定的解.為比較兩種不同計算方法的適用性，針對同一工況，分別采用這兩種方法進行求解.共計算兩種TNT當量(20 kg和50 kg)下，分別計算距離爆心2.0，2.5，3.0，3.5及4.0 m處壓力峰值.具體工況見表3.

表3 自由場爆炸工況

1.4 計算結果分析

自由場爆炸工況下沖擊波載荷在迅速在距離爆心處形成壓力峰值，并隨著沖擊波的傳播壓力峰值不斷減小并開始遠離爆心，傳播規律見圖3.

圖3 工況1作用下壓力云圖

針對工況1～4得到的壓力峰值與Henrych理論公式進行對比分析，分析結果見表4.

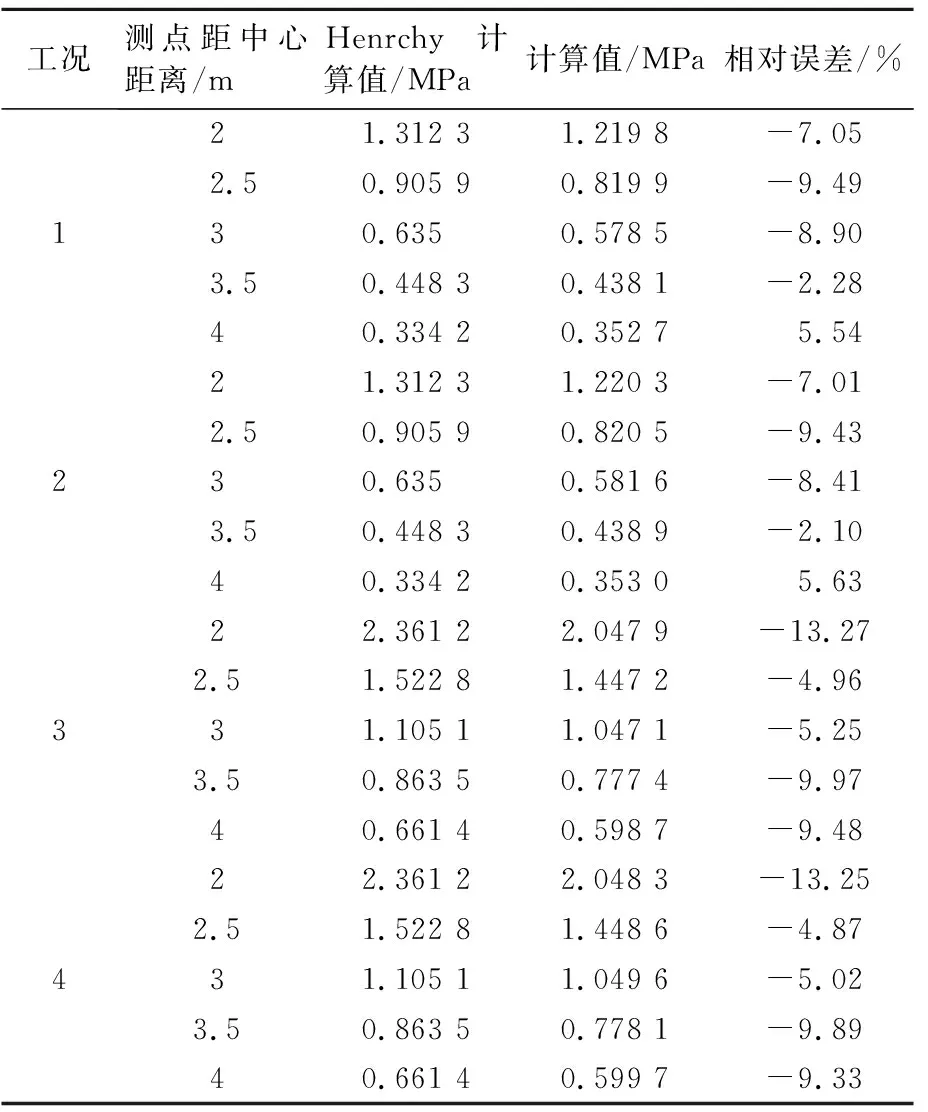
表4 自由場爆炸沖擊波載荷結果對比分析表

計算結果表明，本文采用的仿真計算方法得到的計算結果與理論公式誤差較小，證明有限體積法及ROE兩種空間域的離散方法均可用于TNT爆炸工況下壓力載荷研究的仿真分析研究，后續仿真分析采用ROE方法進行歐拉域的離散.

2 立方體結構艙內爆炸壓力載荷規律研究

艙內爆炸具有瞬態、高度非線性等特點，仿真研究其壓力載荷規律極復雜，為降低仿真分析難度，本節針對標準立方體(1 m×1 m×1 m)鋼質結構進行研究.分別采用一般耦合(GC)和任意拉格朗日耦合(ALE)兩種不同的耦合方法研究了1及3 kg當量TNT內爆工況下，艙室內部準靜態壓力值，并與經驗公式進行對比分析以驗證仿真方法的正確性.同時，研究了裸裝藥在標準立方體內爆工況下，結構角隅處沖擊波載荷匯聚規律.

對于裸裝藥封閉艙室結構內爆工況下準靜態壓力最具代表性的是Carlson等[10-11]提出的計算公式為

p=1.30m/V

(5)

p=(1.34±0.19)m/V

(6)

式中：p為準靜態壓力,MPa；m為炸藥的質量,kg；V為密閉空間的體積,m3.

空氣及炸藥的狀態方程及參數參見表1～2.船體結構為某船用低合金高強鋼，采用Lagrangian單元模擬，其本構關系采用MSC.Dytran中各向同性、具有破壞模式的彈塑性材料(DMATEP)來定義，采用各向同性強化雙線性應力-應變屈服模式和Von Mises屈服準則，材料參數具體見表5.

表5 某船用低合金高強鋼材料參數

立方體模型：Shell單元尺寸為50 mm×50 mm，單元數量為2 400；歐拉單元尺寸為50 mm×50 mm×50 mm單元數量為8 000.內爆工況下TNT當量分別為1，3 kg，藥包位于典型立方體單元的中心.設定三個測試點，分別為面幾何中心點(后續簡稱P1)、兩壁面角隅(后續簡稱P2)、三壁面角隅(后續簡稱P3)，立方體結構有限元模型見圖4.分別采用一般耦合及ALE耦合仿真分析了典型立方體艙室內準靜態壓力值及沖擊波角隅匯聚規律,各計算工況見表6.

圖5給出了p2點處的壓力-時間歷程曲線，并與Carlson及Moir理論公式的結果對比.

計算結果表明，對于準靜態壓力值，立方體仿真計算結果與經驗公式相當吻合，說明本文采用的仿真計算方法合理可行，采用ALE耦合及一般耦合均能合理仿真裸裝藥封閉艙室內爆工況下壓力載荷分析，本文采用的仿真方法可用于實船典型艙內裸裝藥艙內爆炸壓力載荷計算研究.

圖4 立方體結構有限元模型示意圖

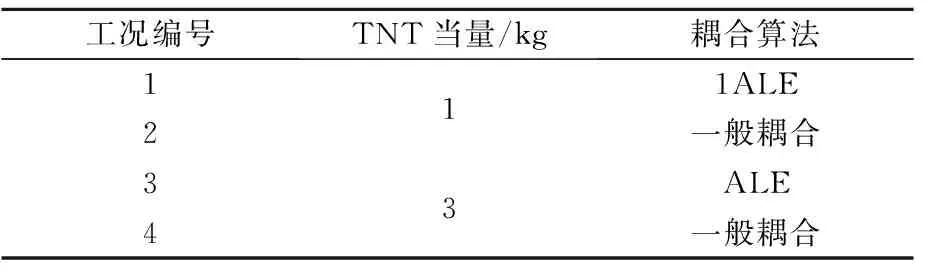
工況編號TNT當量/kg耦合算法1211ALE一般耦合343ALE一般耦合

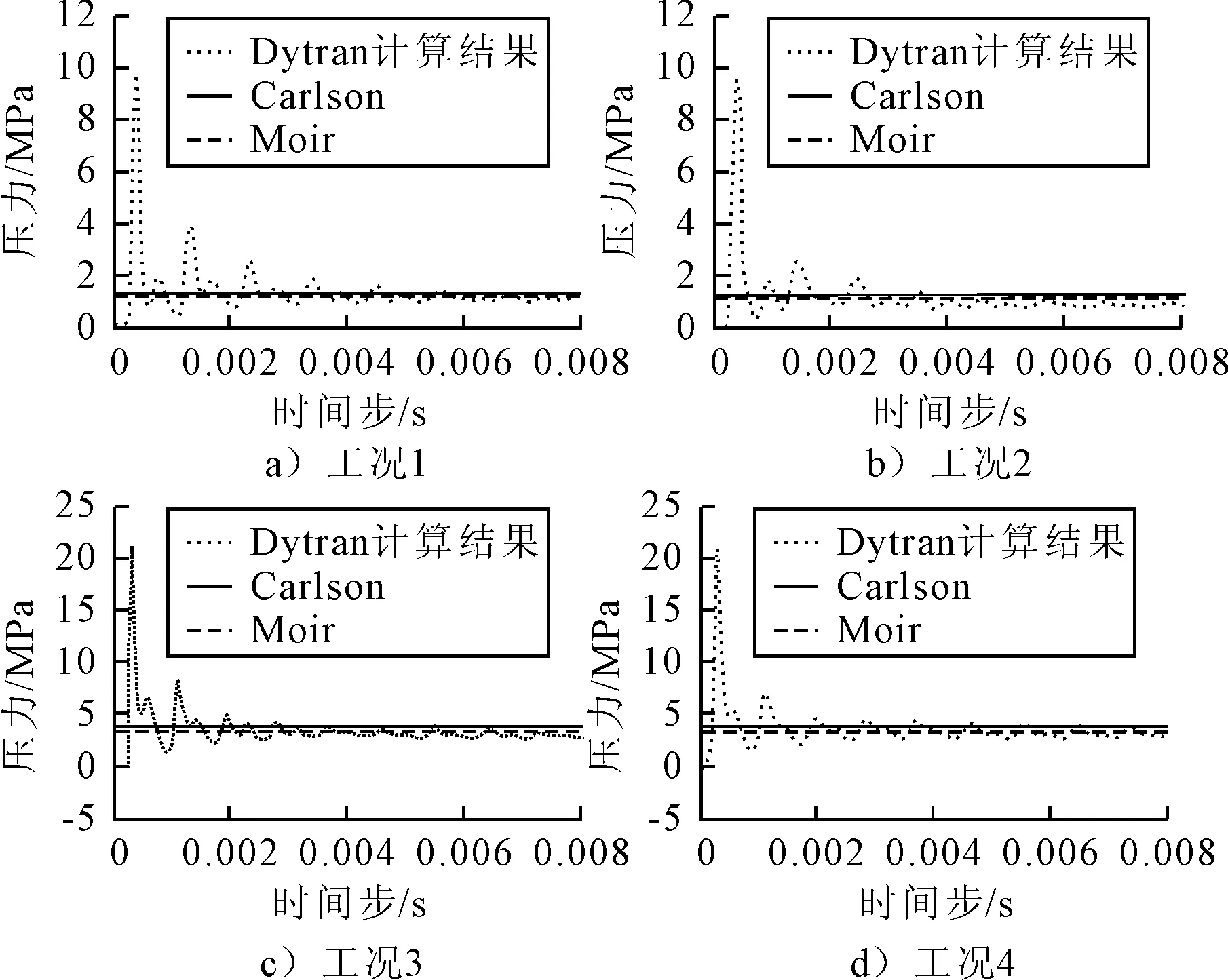
圖5 工況1～4壓力載荷與經驗公式對比圖

圖6計算給出了P1，P2，P3點處的壓力載荷-時間歷程曲線圖，各工況作用下個點的壓力峰值對比分析數據見表7.

圖6 工況1～4各點壓力-時間歷程曲線圖

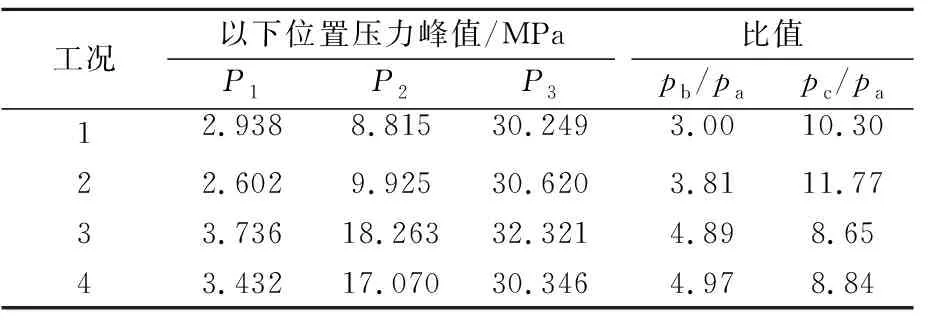
工況 以下位置壓力峰值/MPaP1P2P3比值pb/papc/pa12.9388.81530.2493.0010.3022.6029.92530.6203.8111.7733.73618.26332.3214.898.6543.43217.07030.3464.978.84

計算結果表明：①典型立方體結構，設置的測點P1,P2,P3壓力峰值大小關系為：P3>P2>P1；②P3處的壓力峰值約為P1處壓力峰值的9～12倍，其中P2處的壓力峰值約為P1處壓力峰值的3～5倍.

3 裸裝藥典型艙內爆炸壓力載荷研究

實船艙室結構采用某船用低合金高強鋼具體參數見表5，空氣及炸藥的狀態方程及參數參見表1～表2.本節進一步將實船艙室內爆工況下壓力-時間歷程曲線與Carlson和Moir公式進行進一步對比分析.

典型艙室平面圖見圖7，為簡化計算，將加強筋的板厚均攤至板上.典型艙室有限元模型采用有限體積法離散空氣域，歐拉單元尺寸為54 mm×51 mm×57 mm，單元數量為105 393；結構體單元采用shell單元，單元尺寸50 mm×50 mm，單元數量為157 393；結構單元(Lagrange單元)與空氣域(Euler單元)耦合方式采用一般耦合.有限元模型見圖8.

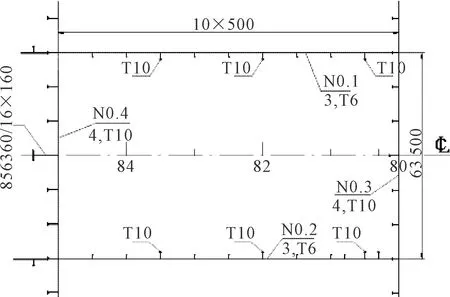
圖7 實船典型艙室平面圖

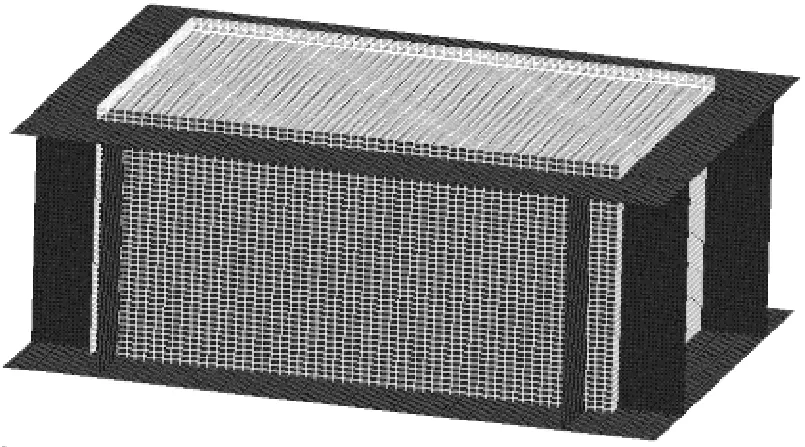
圖8 實船典型艙室有限元模型

計算工況為50 kgTNT，藥包位于艙室幾何中心處.

實船典型艙室載荷輸出點P1，P2及P3分別為No.2艙壁上的幾何中點，兩壁面交線中點及三壁面交點，具體見圖9.

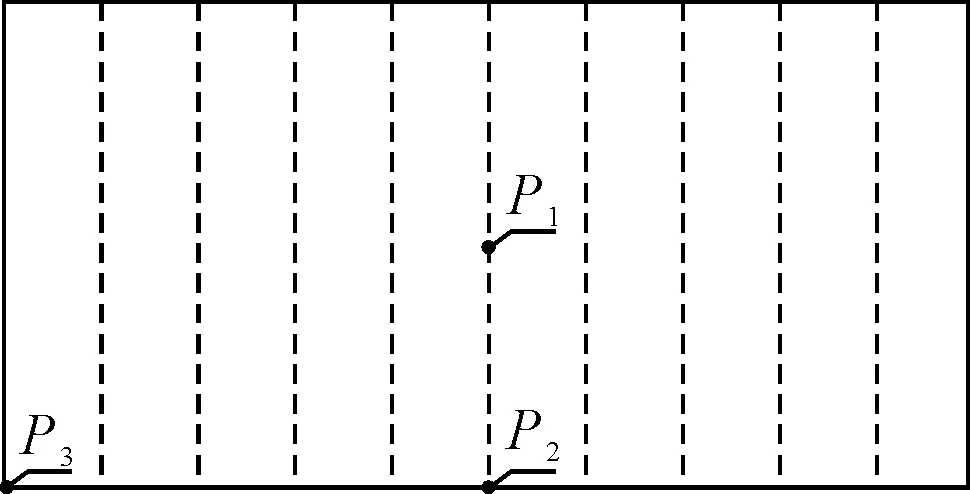
圖9 實船典型艙室載荷輸出點布置圖

采用MSC.Dytran分析計算了50 kgTNT內爆工況下，實船典型艙內爆炸壓力載荷的規律，分別將P3點的載荷-時間歷程曲線與Carlson及Moir公式理論值進行了對比，見圖10；P1,P2及P3測點處的壓力-時間歷程曲線見圖11.

圖10 壓力載荷與經驗公式對比圖

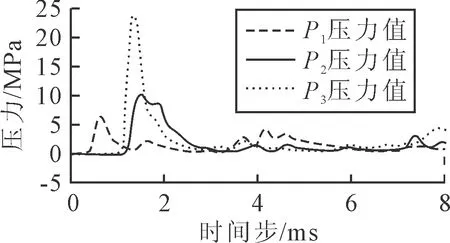
圖11 各點壓力-時間歷程曲線圖

從計算結果分析可知：①采用本文的仿真計算方能夠很好仿真裸裝藥艙內爆炸產生的準靜態壓力；②P3處壓力峰值>P2處壓力峰值>P1處壓力峰值，其峰值分別為23.4、10.3和6.4 MPa；③測點P2和P3距離爆炸點分別是P1的1.3倍和2.1倍，根據空氣中爆炸沖擊波傳播規律P2及P3自由場壓力峰值應遠小于測點P1，但P3處壓力峰值約為P1處壓力峰值的4倍左右，P2處壓力峰值約為P1處壓力峰值的1.5倍.說明內爆工況下沖擊波載荷會在艙室角隅產生明顯的匯聚效應.

4 結 論

1) 有限體積法及ROE方法均可作為歐拉域的離散方法，一般耦合方法及ALE方法均可作為流-固耦合方法.

2) 本文仿真方法可有效模擬裸裝藥在封閉艙室內爆工況下的準靜態壓力值，計算結果與Carlson、Moir等經驗公式計算結果吻合較好.

3) 對于封閉艙室裸裝藥內爆工況下，沖擊波載荷會在艙室角隅處產生明顯匯聚效應，P3處壓力峰值>P2處壓力峰值>P1處壓力峰值.

4) 對于典型立方體結構，兩壁面角隅匯聚沖擊波的峰值約為相同部位第一次沖擊波壓力峰值的3～5倍，三壁面角隅匯聚沖擊波的峰值為相同部位第一次沖擊波壓力峰值的9～12倍.

5) 對于越接近立方體的艙室結構，在艙室角隅處越易形成壓力波峰的疊加效應，則角隅處壓力峰值較相同部位壓力峰值的比值越大，故沖擊波在長方體結構匯聚效應不如立方體結構明顯.

6) 裸裝藥艙內爆炸載荷規律由于其瞬態、高度非線性等特點，一直以來是艦船抗爆結構設計難點，本文給出了MSC.Dytran仿真分析該問題的適當方法為艦船抗爆結構設計提供了支撐.計算得到的內爆工況下沖擊波載荷的匯聚效應及準靜態壓力的特點反映出艙室角隅結構是艦船抗爆結構設計的重點.