適用不同粒徑含鹽砂壤土水分擴散率的通用模式

古萊姆拜爾·艾爾肯，虎膽·吐馬爾白,馬合木江·艾合買提

(新疆農業大學水利與土木工程學院 ，新疆 烏魯木齊 830052)

土壤水分運動參數包括土壤水分擴散率D(θ)、導水率K(θ)以及比水容量C(θ)，這些參數綜合反映了土壤的持水性能及運移能力[1]。土壤水分擴散率反映了土壤孔隙度、孔隙大小分布以及導水性能，它是表征土壤水動力學的重要參數之一，并影響土壤中水分運動狀況[2-3]。土壤水分擴散率也是研究水鹽運動規律與調控的主要參數[4]。土壤擴散率受質地、粘粒含量、土壤密度、孔隙度和有機質等諸多因素的影響[5]。因此，半干旱地區土壤水分擴散率的研究具有極其重要的理論和實踐意義，早已為人們所重視。長期以來，很多學者針對干旱、半干旱地區做了大量的研究工作[6-9]，但是研究土壤鹽分對土壤水分擴散率的影響較少見。

用水平入滲實驗計算土壤水分擴散率的方法最早是由Bruce和Klute提出的[10]。該方法是利用一個半無限長的水平土柱來進行入滲試驗，忽略重力作用，根據一維水平流動的偏微分方程和定解條件，引入Boltzmann變換參數后，將偏微分方程化為常微分方程，用解析法求得計算公式，再由試驗資料列表計算土壤水分擴散率[11]。隨后，Kirkham和Powers[12]詳細論述了這種方法的應用。因為該方法的關鍵是獲得土壤水分分布的光滑曲線，因此得到了廣泛應用[13-20]。此法為室內測定D(θ)的重要方法，在非飽和土壤水分運動研究中起到了重要作用。

土壤中的鹽分運動十分復雜，鹽分一般隨著土壤水分的運動而遷移。由于新疆石河子121團是典型的重鹽堿土，因此確定含鹽土中水溶質運動的綜合擴散系數是十分必要的。對鹽堿地土壤水鹽運動的定量描述是控制區域土壤次生鹽堿化的基礎，其中的土壤水分擴散率是研究土壤水鹽運動不可缺少的參數之一[21-23]。本研究在建立Boltzmann變換參數η與土壤體積含水率θ定量函數關系的基礎上，采用類似于Bruce和Klute的方法對新疆石河子121團灌區膜下滴灌棉田不同粒徑含鹽砂壤土土壤水分擴散率進行比較,以及對土壤鹽分運動規律進行研究。通過水分擴散率的測定可定量模擬單位時間內土壤水分擴散率的距離及其與含水率之間的關系，預測土壤次生鹽堿化的發展速度，為土壤次生鹽堿化的監測與防治提供理論依據。

1 試驗地概況

試驗在新疆石河子121團進行，該團位于天山北麓，準噶爾盆地南緣，E85°20′～85°48′，N44°45′～44°58′。該地屬于溫帶大陸性氣候，日照時間長，年平均日照時間2 864 h，最高氣溫35℃，無霜期達160 d，年降水量140.2 mm,平均蒸發量1 789.2 mm，地下水埋深3～5 m，土壤質地為砂壤土。0～100 cm土層平均體積質量1.48 g·cm-3,田間持水率為20.6%(重量含水率)。

2 材料與方法

2.1 采樣方法與數據測定

土樣采自新疆石河子121團試驗地，采用50 m×50 m網格取樣，用自封袋裝擾動土土樣，采集117點共702個土樣樣品，試驗地面積為450 m×650 m。土壤容重采用環刀法測定；土壤顆粒分析是用國際SL237-1999中密度計法測定顆粒組成，土壤類型由美國土壤類型三角圖確定。其中粉粒占0.7%(0.002～0.05 cm)，粘粒占23.7%(<0.002 cm)，砂粒占75.6%(0.05～2 cm),土壤質地為砂質壤土，經自然風干后的土壤過0.5、0.5～1.0 mm和1.0～2.0 mm篩，按1.40 g·cm-3容重裝入水平土柱中。

2.2 測定原理

測定原理參見文獻[24]。在水平土柱中，使進水端維持接近飽和的穩定邊界的土壤含水率，使水分在土柱中作水平滲吸運動，在不計重力影響的條件下進行測定。其一維水平流的微分方程和定解條件為：

(1)

θ(x,t)=θix>0,t=0

(2)

θ(x,t)=θs,x=0,t>0

(3)

式中,t為時間(min)，x為水平入滲距離(cm)，D(θ)為非飽和土壤水分擴散率(cm2·min-1)，θi為水平土柱初始含水率，θs為飽和含水率(開始試驗后在邊界處瞬時形成)

對式(1)進行波爾茲曼變換(Boltzmann),利用定解條件(2)和(3)式，可以求得：

(4)

式中,η為波爾茲曼參數，η=xt-1/2。

為了便于計算，通常將式(4)改變為差分的形式，其表達式為：

(5)

通過對(5)式的計算，便可根據實驗數據，用列表法計算土壤水分擴散率D(θ)。

2.3 實驗裝置

水平土柱試驗裝置見圖1，土柱由有機玻璃圓筒(內徑為4.6 mm)組成。試樣段由13個長4 cm的圓環組成。在進水邊界處(x=0)，為保證土壤體積含水率為飽和含水率但又不產生重力水流的條件，在進水室與土柱之間裝設低氣泡壓力和高傳導率的多孔板或濾網。供水裝置用以控制水平土柱的作用水頭(可考慮保持土柱作用水頭略低于大氣壓力)，測量進水量。

圖1 土壤水分擴散率試驗裝置示意圖Fig.1 Schematic diagram of test equipment for determining soil water diffusivity

2.4 實驗步驟

(1)制備土樣及裝填土柱，準備好足夠的試樣(風干含水量)。按一定容重裝填土柱，將螺桿旋緊然后水平放置。(2)瞬時給進水室充水并使供水裝置定位。(3)計時并記下供水箱初始水位讀數。(4)經過相當時間(濕潤鋒面未達土柱末端之前)后，即可結束試驗，此時停止供水，松開堅固螺桿，按節取出土壤測定含水率，記下整個試驗的歷時及總水量。3個重復試驗。(5)利用烘干法將烘干土樣粉粹，取土水比例1∶5攪拌均勻，沉淀后利用DDSJ-308A土壤含鹽率儀測定土壤的含鹽率(3個重復)。

3 結果與分析

3.1 土壤體積含水率與Boltzmann變換參數和土壤含鹽率的關系

通過非穩定流水平土柱試驗，得到三組試驗數據，用式η=xt-1/2算出不同θ值對應的η值，并繪制θ-η曲線(圖2)，Boltzmann參數η=xt-1/2(x為水平入滲距離，t為時間)反映了水分在土壤中水平入滲時，濕潤峰向前移動的快慢程度[7]。在進水端土壤體積含水率接近飽和，Boltzmann變換參數應為零；當土壤體積含水率取初始體積含水率時，Boltzmann變換參數趨于無窮大。從圖可知土壤體積含水率隨著Boltzmann變換參數的增大而減少。

對粒徑<0.5 mm、0.5～1.0 mm和1.0～2.0 mm，當體積含水率范圍分別在0.367、0.332、0.317 cm3·

圖2 土壤體積含水率(θ)與Boltzmann參數(η)的關系Fig.2 Relationship between soil water content θ and Boltzmann transformation parameter η

cm-3以上時，Boltzmann變換參數隨體積含水率緩慢下降；在體積含水率低于0.367、0.332、0.317 cm3·cm-3時，隨著體積含水率的降低，Boltzmann變換參數迅速下降。

土壤鹽分一般隨著土壤水分的運動而遷移。由土壤體積含水率與土壤含鹽率的變化關系(圖3)可知，土壤含鹽率隨著土壤體積含水率的增大而減少，<0.5 mm粒徑的砂壤土的含鹽率最高；接下來是0.5～1.0 mm粒徑的砂壤土；最低的是1.0～2.0 mm粒徑的砂壤土。這是因為土壤累計入滲時間和總入滲水量隨著粒徑的增大而減少。土壤含鹽率與土壤體積含水率的關系可用線性函數來表示(表1)。從土壤體積含水率與Boltzmann變換參數和土壤含鹽率之間的關系分析可知Boltzmann變換參數和土壤含鹽率隨著土壤體積含水率的增大而減少。

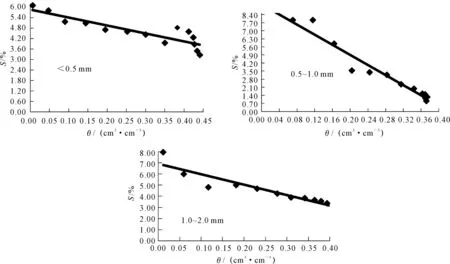
圖3 土壤體積含水率(θ)與土壤含鹽率(S)的關系Fig.3 Relationship between soil water content (θ)and soil salt content (S)

3.2 土壤體積含水率與土壤水分擴散率的關系

根據實驗數據計算不同體積含水率對應的土壤水分擴散率，并繪制土壤體積含水率與土壤水分擴散率的關系曲線(圖4)。

從圖中可以看出，對于同一容重、相同水平距離情況下粒徑不同時含鹽砂壤土的土壤水分擴散率隨土壤體積含水率的增加而增加。當含水率接近飽和時，水分擴散率趨于無窮。1.0～2.0 mm的砂壤土擴散率最大，而且變化比較迅速，其次0.5～1.0 mm的砂壤土，最小的是小于0.5 mm的砂壤土。這表明土壤機械組成對土壤水分擴散率有較大的影響，表現為隨著土壤粒徑的減小，土壤水分擴散率逐漸降低。這與Xie Senchuan等[25]的砂性土的非飽和土壤水分擴散率大于粘性土的結論一致。用指數函數擬合土壤水分擴散率與土壤體積含水率之間的關系，具體結果見表2。

3.3 土壤水分擴散率的綜合通用表達式

在實際情況中，僅僅土壤體積含水率與土壤水分擴散率的經驗公式受到一定的限制，不能較好地反映出土壤水分擴散率的變化曲線。因此要找到一個計算不同粒徑含鹽沙壤土水分擴散率的通用公式。

表1 土壤體積含水率與土壤含鹽率的線性函數擬合分析

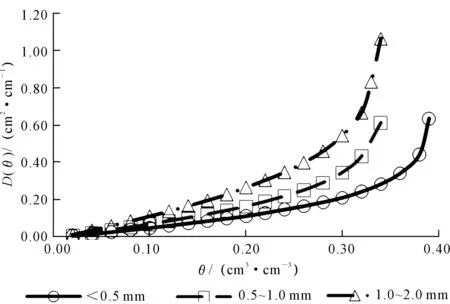
圖4 土壤體積含水率θ與土壤水分擴散率D(θ)的關系曲線Fig.4 Relationship between soil water content (θ) and soil water diffusivity D(θ)

由土壤體積含水率與土壤含鹽率的變化關系可知，土壤含鹽率隨著土壤體積含水率的增大而減少，土壤含鹽率與土壤體積含水率的關系可用線性函數來表示(表1)。通過分析土壤體積含水率與土壤含鹽率之間關系，再結合土壤體積含水率與土壤水分擴散率之間關系，可知土壤含鹽率隨著土壤水分擴散率的增大而減少。本文通過上述分析了土壤水分擴散率與土壤體積含水率和土壤含鹽率的變化關系，得到了土壤水分擴散率的綜合表達式(見表3)。試驗分析得出，同一容重、相同水平距離情況下粒徑不同時含鹽沙壤土擬合的經驗公式，擬合程度和回歸程度較好。

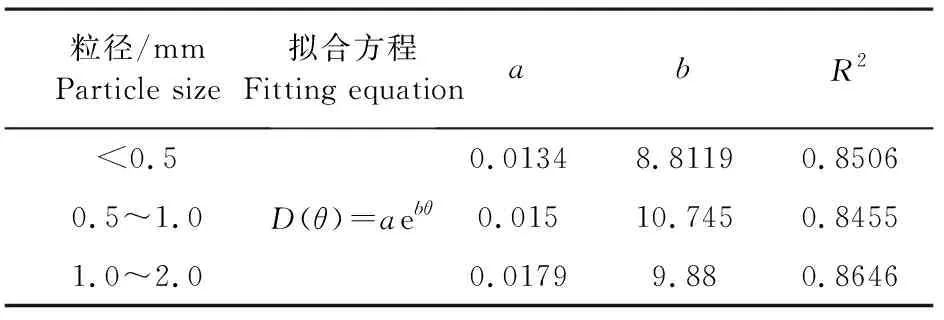
表2 土壤體積含水率與土壤水分擴散率的指數函數擬合分析

表3 土壤水分擴散率的綜合表達式

4 結果與討論

1)對于同一容重、相同水平距離情況下粒徑不同時含鹽砂壤土的土壤體積含水率與土壤水分擴散率呈單調遞增關系。1.0～2.0 mm的砂壤土擴散率最大，而且變化比較迅速，其次為0.5～1.0 mm的砂壤土，最小的是小于0.5 mm的砂壤土。隨著土壤粒徑的減小，土壤水分擴散率在逐漸降低。當土壤體積含水率接近飽和時，水分擴散率趨于無窮。

2)對于同一容重、相同水平距離情況下粒徑不同時含鹽砂壤土的土壤含鹽率與土壤水分擴散率呈單調遞減關系。<0.5 mm粒徑的砂壤土的含鹽率最高，其次為0.5～1.0 mm粒徑的砂壤土,最低的是1.0～2.0 mm粒徑的砂壤土。

3)新疆鹽堿地土壤面積較大，土壤水分運動參數計算中考慮土壤的含鹽量是較為符合實際。土壤水分擴散率D(θ)的通用模式中綜合考慮土壤體積含水率和土壤含鹽率，得出的經驗公式能夠較好地反映不同粒徑含鹽砂壤土的土壤水分擴散率。