多潮位站海道地形測量潮位控制方法研究

，，，

(1.長江水利委員會水文局 長江三峽水文水資源勘測局，湖北 宜昌 443000；2.長江宜昌航道局，湖北 宜昌 443000)

隨著沿海及近海地區的開發與利用，海洋航運、港口碼頭修建、漁業養殖等人類活動愈加頻繁，對海洋的分析研究要求也越來越高，這勢必會對獲取的海洋信息的詳細程度要求越來越高[1]。大面積海洋測繪精度已經逐步實現了由小比例尺測繪資料向中小比例尺資料的過渡。因此，傳統的通過用沿岸設立潮位站[1]，對大面積海域的測量資料進行單站潮位改正的測繪方式已經無法滿足精度的要求，需將目光投向對測量資料進行多站潮位改正這一研究方向。然而受海洋潮汐、地球曲率、涌浪等諸多外界因素的影響，多潮位站海道地形測量對潮位站的布設、基面關系的確定以及潮位改正方法的要求較為嚴格。雖然針對每種技術要求都有多種處理方法，但多潮位站海道地形測量的綜合性較強，難度較大，從而導致該類項目實施困難。

本文主要對多潮位站海道地形測量潮位控制、基面計算與傳遞、潮位改正方法等方面進行分析研究，提出切實可行的技術路線，以便于進一步指導實際工作中多潮位站海道地形測量潮位控制方法問題。

1 測量關鍵技術原理分析

多潮位站海道地形測量關鍵技術有兩個。

(1)潮位控制問題。包括臨時潮位站布設、臨時潮位站數據聯測和潮位改正方法。沿岸臨時潮位站的布設較為簡單，且潮位站零點可通過水準測量等方法聯測求得。而海上臨時潮位站的布設較為困難，既要求水位計固定不動、安全穩定，又要求零點高程準確可求，這對技術和設備的要求較高。

(2)基面計算與傳遞。與陸地測量或內河地形測量不同，海洋測量有其獨特的基準起算面，即深度基準面。我國多用理論最低潮面來定義深度基準面。如何解決不同測區理論最低潮面的計算與傳遞就成為一大關鍵問題。

下面針對這兩大關鍵問題所要求的技術原理進行分析和闡述。

(1)最小二乘擬合模型。對于海上臨時潮位站的零點推算最為精確可靠的方法，是根據沿岸基準潮位站與海上潮位站潮位曲線的相關性分析，采用最小二乘擬合模型推算[2]。

如圖1所示，以時間為X軸，潮位值為Y軸，曲線TA(t)與TB(t)為兩個臨時驗潮站同步潮位曲線，兩條同步潮位曲線存在3個參數的差異：水平位移即兩潮位間的潮時差δAB；垂直位移即兩驗潮站的基準面偏差εAB(應用到本文為兩驗潮站的水尺零點差)；同步潮位值的比值即潮差比γAB。曲線TA(t)與TB(t)存在以下關系：

TB(t)=γABTA(t+δAB)+εAB

(1)

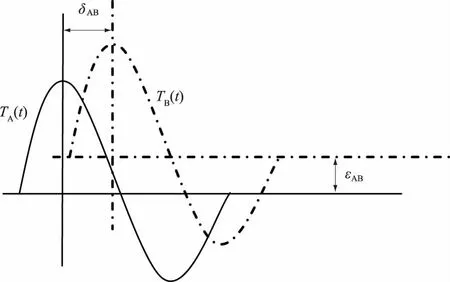
圖1 最小二乘擬合法模型

(2)半潮差法。當臨時潮位站附近有一個長期或短期潮位站時，臨時潮位站的理論最低潮面可通過長期或短期潮位站的基面關系推算求得。根據《水運測量規范》(JTS131-2012)[3]所述，在大潮期同步觀測兩站潮位2～3 d，計算同步期平均海面。兩站潮差差值不大于 0.1 m時，臨時潮位站的深度基準面與同步期平均海面的高差，可借用鄰近長期或短期潮位站的深度基準面與同步期平均海面的高差值；當兩站潮差差值大于0.1 m時，臨時潮位站深度基準面與同步期平均海面的高差應按下式計算：

(2)

式中，L′x為臨時潮位站深度基準面與同步期平均海面的高差，m；L為長期潮位站深度基準面與同步期平均海面的高差，m；Px為臨時潮位站同步期的平均半潮差，m；P為長期潮位站同步期的平均半潮差，m。

(3)潮汐調和分析。當臨時潮位站附近無長期潮位站或長期潮位站離測區較遠，可根據潮汐調和分析求解臨時潮位站的基面轉換關系。

由潮汐理論[4]知，海洋中的潮汐主要是由月球和太陽對地球的引潮力所致。所謂調和分析，就是把由月球等天體引起的復雜的潮汐現象，分離成由許多假想天體相對于地球作均速圓周運動而產生的潮汐(即分潮)之和。即對某一潮位站，在任意t時刻的潮高h(t)可表示為

h(t)=H0+

(3)

其中，H0為平均海平面；fk為節點因子；Rk為分潮角速度；(v0+u)k為分潮初相；Hk,gk為分潮調和常數。

利用M2、S2、N2、K2、K1、O1、P1、Q1、M4、MS4、M6、Sa、Ssa等13個分潮的調和常數，根據弗拉基米爾法可計算出理論最低潮面與高程基準的基面偏差。

(4)二步內插法潮位改正[5]。設A1、A2、A3三個潮位站某時刻的潮位分別為Z1、Z2、Z3，求P點的潮位，如圖2。

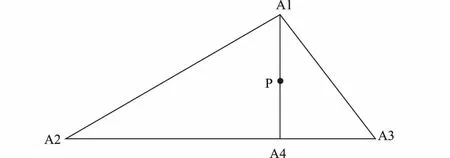
圖2 二步內插法示意

由A1、A2、A3和P的坐標，可聯解求得A2A3與A1P兩個直線方程，得出A4的坐標，然后在直線A2A3上以這兩點潮位按距離內插得到A4的潮位;再在直線A1A4上，以A1A4的潮位線性內插求得測點P的潮位:

ZP=(Z4-Z1)/SA1A4×SA1P+Z1

(4)

Z4=(Z2-Z3)/SA2A3×SA4A3+Z3

(5)

式中，SA1A4、SA1P、SA2A3和SA4A3分別為A4與A1、A1與P、A2與A3和A4與A3的距離。

2 多潮位站海道地形測量潮位控制應用

(1)潮位站布設。以江蘇鹽城射陽港水下地形測量項目為例，為滿足規范規定潮位控制要求，在沿岸布設1，2，3號3個臨時潮位站，其中射陽河口碼頭站2號為基準驗潮站，連續觀測1個月，用于潮位調和分析。測區遠岸端臨時潮位站4號拋投水位自記儀。潮位站分布圖如圖3所示。

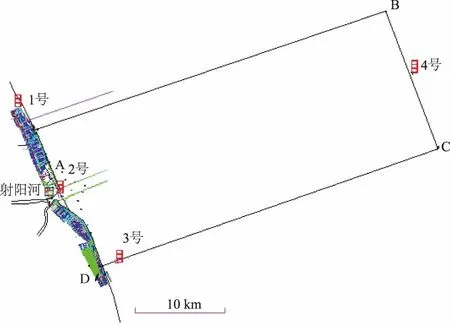
圖3 臨時潮位站位置

(2)臨時潮位站零點聯測。對于1，2，3號岸邊潮位站的零點可通過水準聯測和人工比測數據計算潮位站水尺零點。位于海上的4號潮位站，無法通過水準聯測的方式確定水尺零點，采用最小二乘擬合傳遞推估技術(曲線擬合法)傳遞臨時潮位站的水尺零點。

(3)基面計算與傳遞。該次實驗數據中各潮位站的1985國家高程基準與理論最低潮面之間的基面關系采用兩種方法相互驗證，確保基面關系的準確性。

方法一是在射陽河口“2號”收集30 d的潮位觀測資料，采用潮汐調和分析法計算出M2、S2、N2、K2、K1、O1、P1、Q1、M4、MS4、M6等11個分潮的調和常數；Sa、Ssa分潮的調和常數，由長期驗潮站連云港站(射陽港北120km)1 a以上的潮位觀測資料求得，最后采用弗拉基米爾法計算出理論最低潮面與1985國家高程基準的基面偏差。

方法二是收集附近長期驗潮站大豐站(射陽港南約60 km)與射陽河口2號一個月的同步潮位數據，以及大豐站1985國家高程基準與理論最低潮面的關系，根據交通運輸部《水運測量規范》(JTSB1-2012)[3]7.4.4.3中所述方法，將基面關系傳遞到測區。

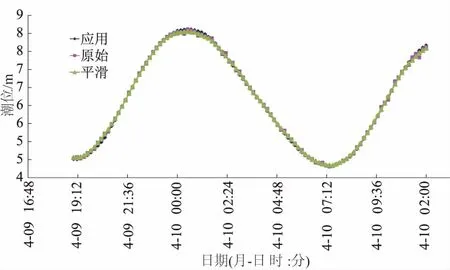
圖4 潮位數據預處理示意

3 實驗數據處理與分析

(1)潮位數據預處理。由于海洋環境惡劣，受涌浪、行船等因素的影響，水位自記儀原始記錄數據多為鋸齒狀，為了得到真實平滑的潮位資料，需要對原始潮位資料做平滑預處理。方法有小波濾波處理[6]、MATLAB平滑擬合函數、人工干預等，本次采用MATLAB平滑擬合函數方法。

如圖4所示，洋紅色鋸齒狀曲線表示原始水位數據，灰色表示經過平滑擬合后的數據，藍色表示實際應用潮位數據。由圖可以看出，漲落潮時使用平滑擬合函數與實際潮位數據吻合較好，高低平潮時擬合數據與實際值有一定出入，需要人工干預處理。

(2)潮位站零點聯測。沿岸臨時潮位站可通過水準聯測方式測出潮位站基點高程，再通過每天高低潮時人工驗潮比測推算潮位站零點高程；海上臨時潮位站通過最小二乘擬合模型傳遞。1985國家高程基準的水尺零點最小二乘擬合成果見表1。

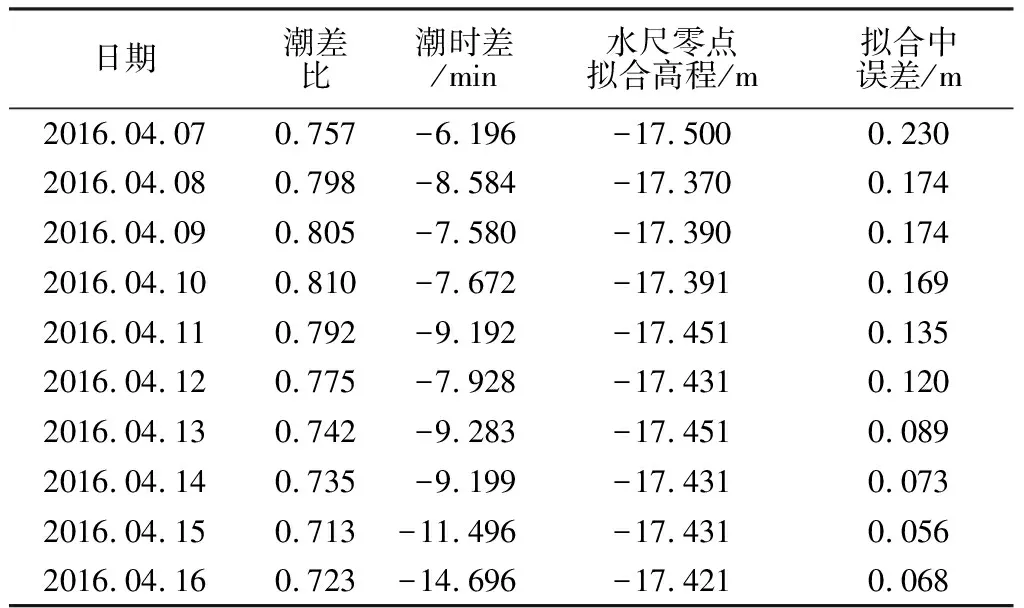
表1 射陽河口“4號”最小二乘擬合成果

注：水尺零點采用-17.43 m。

(3)基面計算與傳遞。方法一是采用潮汐調和分析法求解，即在測區基準驗潮站，射陽河口“2號”對該站30 d的潮位觀測資料，采用潮汐短期調和分析法計算出M2、S2、N2、K2、K1、O1、P1、Q1、M4、MS4、M6等11個分潮的調和常數，見表2。

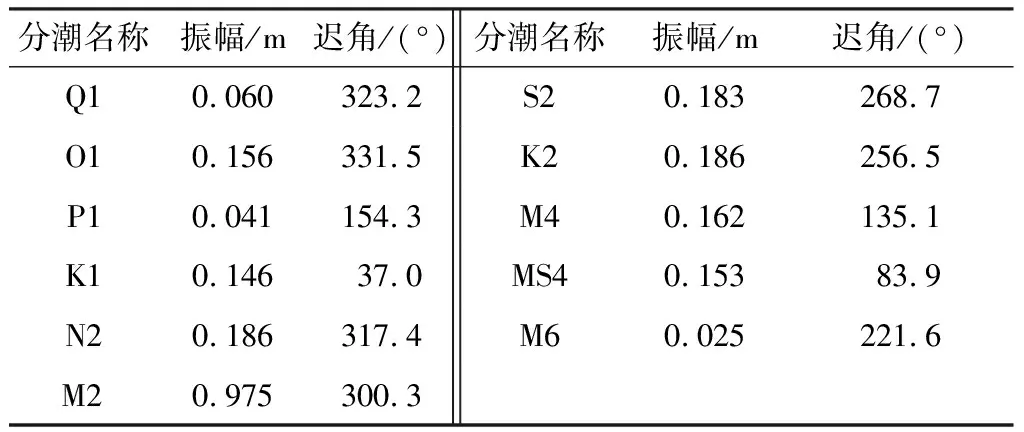
表2 短期調和分析成果

收集附近長期站1 a以上的潮位觀測資料，采用潮汐長期調和分析法求解Sa、Ssa分潮的調和常數，由于該項目沒有收集到長期站1 a的潮位觀測資料，現用連云港2007年全年潮位資料做數據分析，調和分析成果見表3。

表3 長期調和分析成果

最后采用弗拉基米爾法計算出理論最低潮面在平均海平面下的高度L為1.93 m。平均海平面的計算采用面積包圍法，求解同步期平均海平面的高程M為0.19 m。理論最低潮面的1985國家高程基準高程H=L-M=1.74 m。

方法二是根據長期潮位站大豐站理論最低潮面與1985國家高程基準的基面關系，采用半潮差法將基面關系傳遞到測區臨時水位站。大豐站基面關系見圖5。平均半潮差P=1.81 m，1985國家高程基準平均海平面D=0.21 m。“2號”潮位站基面關系見圖6。平均半潮差PX=1.13 m，1985平均海平面DX=0.18 m。

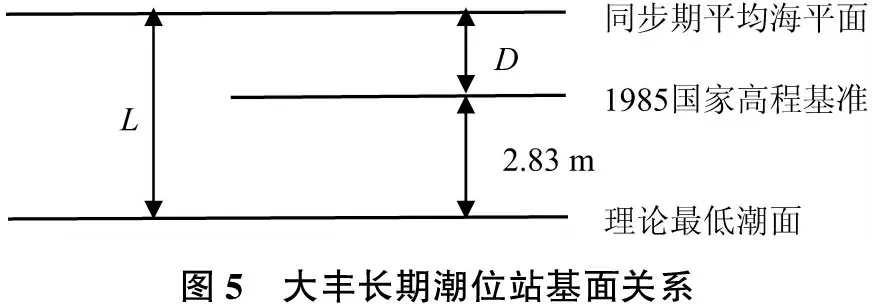
圖5 大豐長期潮位站基面關系

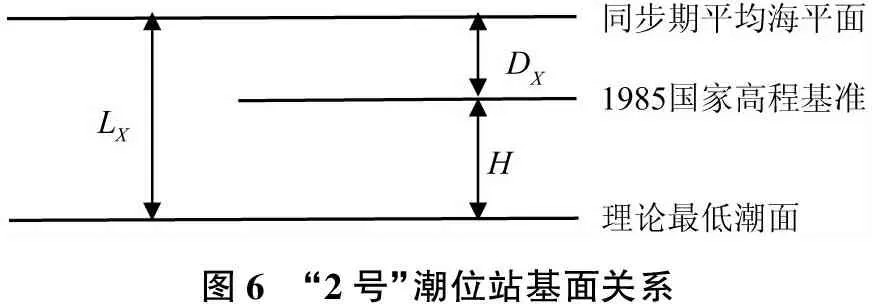
圖6 “2號”潮位站基面關系

由上面分析可以看出，通過兩種方法推算基準站“2號”站的基面轉換關系符合性較好。

(4)潮位改正。對測區數據進行分區處理，采用HYPACK三站潮位改正模塊內插出各個水深點的潮位，進行逐點潮位改正。

4 結 語

本文對多潮位站海道地形測量潮位控制方法進行研究，著重對潮位控制和基準面計算與傳遞進行分析。針對潮位站零點傳遞問題，引入潮位改正中的最小二乘擬合原理，有效地解決了海上臨時潮位站基面傳遞問題。針對測區理論最低潮面的計算問題，采用半潮差法與潮汐調和分析法相互驗證，確保求解的基面關系準確可靠。