基于CEGAR的C程序空指針解引用檢測
段 釗 田 聰 段振華
(西安電子科技大學(xué)計算機(jī)理論與技術(shù)研究所 西安 710071)
(ctian@mail.xidian.edu.cn)
?
基于CEGAR的C程序空指針解引用檢測
段釗田聰段振華
(西安電子科技大學(xué)計算機(jī)理論與技術(shù)研究所西安710071)
(ctian@mail.xidian.edu.cn)
CEGAR Based Null-Pointer Dereference Checking in C Programs
Duan Zhao, Tian Cong, and Duan Zhenhua
(InstituteofComputingTheoryandTechnology,XidianUniversity,Xi’an710071)
AbstractWith the rapid growth of computer software in both scale and complexity, more and more attention has been paid by software developers on the reliability and security issue. Null-pointer dereference is a kind of errors which often occur in programs.This paper proposes a CEGAR based null-pointer dereference verification approach for C programs. With this method, first, a linear temporal logic (LTL) formula is used to specify the null-pointer dereference problem. Then whether null-pointer dereference occuring in a program is checked by a CEGAR based model checking approach. In order to verify null-pointer dereference problem in a total automatic way, this paper also studies how to generate temporal logic formulas automatically with respective to null-pointer dereference problem. Experimental results show that the proposed approach is useful in practice for checking null-pointer dereference in C programs with large scale.
Key wordsmodel checking; abstraction refinement; null-pointer dereference; program verification; temporal logic
摘要隨著計算機(jī)軟件規(guī)模和復(fù)雜度的日益增長,軟件系統(tǒng)的可靠性和安全性倍受關(guān)注.空指針解引用是程序中常見的一類錯誤.提出了一種基于反例制導(dǎo)抽象精化CEGAR的C程序空指針解引用檢測方法.該方法首先使用線性時序邏輯描述空指針解引用問題,然后通過抽象精化的方法檢測待測程序中是否含有空指針解引用錯誤.為了達(dá)到完全自動驗(yàn)證的目標(biāo),同時針對空指針解引用問題,研究了該類性質(zhì)的時序邏輯表達(dá)方法,并自動從程序中針對所有的指針變量,形成相應(yīng)的時序邏輯公式.實(shí)驗(yàn)結(jié)果表明,所提出的方法在大規(guī)模C程序的空指針解引用檢測方面有著重要的實(shí)際應(yīng)用價值.
關(guān)鍵詞模型檢測;抽象精化;空指針解引用;程序驗(yàn)證;時序邏輯
計算機(jī)軟件已深入到國防建設(shè)和國計民生的各個領(lǐng)域,如航天航空、工業(yè)控制、交通、醫(yī)療、教育和社交等,成為當(dāng)今社會不可或缺的一部分.面對多樣化的需求,軟件的規(guī)模和復(fù)雜性不斷增大,因而軟件的可靠性和安全性更加難以得到保障.目前,大部分軟件系統(tǒng)都存在各種各樣的錯誤和缺陷.有的軟件雖然可以正常運(yùn)行,但是其內(nèi)部仍然存在許多錯誤隱患,在特定情況下會導(dǎo)致軟件性能下降,甚至引起程序崩潰,從而造成巨大的損失.為了提高軟件的可信性,研究人員提出大量的技術(shù)來檢測和預(yù)防軟件中的錯誤和缺陷.
C程序中指針的使用十分廣泛,而且語法靈活,但易錯.由于指針而引發(fā)的內(nèi)存錯誤往往難以追蹤和分析,空指針解引用是其中常見的錯誤之一.如果一個指針表達(dá)式指向NULL,或者未被初始化,或者指向一個已被釋放的內(nèi)存,那么,使用該表達(dá)式的解引用就會導(dǎo)致系統(tǒng)崩潰或者得到錯誤的數(shù)據(jù).
許多查找軟件錯誤的技術(shù)被提出.其中,靜態(tài)分析是在不執(zhí)行程序的情況下通過直接分析源程序來檢查程序中的錯誤,主要包括路徑敏感不敏感分析方法[1]和流敏感不敏感分析方法[2-3]等.程序測試[4-5]是對程序的每一個模塊在使用前進(jìn)行測試,保證該模塊的正確性.定理證明[6]將待測問題轉(zhuǎn)化為可滿足性問題,通過判斷命題邏輯公式的可滿足性來檢測程序中是否存在錯誤.模型檢測[7-8]主要是把待檢測程序描述為狀態(tài)遷移系統(tǒng),把待檢測的問題用時序邏輯公式表示出來,然后檢測狀態(tài)遷移系統(tǒng)是否滿足性質(zhì).近年來,許多研究將模型檢測、定理證明和靜態(tài)分析等技術(shù)相結(jié)合,利用各種方法的優(yōu)勢來檢測程序中的錯誤.
在空指針解引用方面,Dirk等人開發(fā)的自動驗(yàn)證工具BLAST[9-11],可以驗(yàn)證C程序中的安全性質(zhì).Dirk等人將他們的方法進(jìn)行了擴(kuò)展,開發(fā)了新的工具CPAChecker[12-13].但是使用BLAST和CPAChecker檢測程序中的空指針解引用需要預(yù)先在程序中插樁,如何完全自動地插樁是一個有待解決的實(shí)際問題.CMBC[14]是Edmund等人開發(fā)的一種限界模型檢測工具.Charatonik等學(xué)者在此工具的基礎(chǔ)上,通過限界的思想來檢測程序中是否存在空指針解引用問題[15].另外,還有一些研究針對并行程序中空指針解引用問題[16].在國內(nèi),也有一些學(xué)者從事這方面的研究,如文獻(xiàn)[17]給出了一種檢測C程序中基于區(qū)域內(nèi)存模型的空指針解引用錯誤的方法.
總之,現(xiàn)有的程序模型檢測方法和工具很多,它們主要是通過對源程序進(jìn)行插樁,然后再分析插樁后的程序.CBMC和BLAST支持對程序的自動插樁;但是,它們是對程序中每個指針的每一次解引用都進(jìn)行插樁,因而會大大增加源程序的代碼量.CPAChecker則需要手動地進(jìn)行插樁,如果給每個位置插樁,同樣會增加代碼量.
本文提出了一種基于反例制導(dǎo)抽象精化(counter example-guided abstraction refinement, CEGAR)[18]的C程序空指針解引用檢測方法.該方法首先使用線性時序邏輯(linear temporal logic, LTL)描述空指針解引用問題,然后通過抽象精化的方法檢測待測程序中是否含有空指針解引用錯誤.為了達(dá)到完全自動驗(yàn)證的目標(biāo),本文同時針對空指針解引用問題,研究了該類性質(zhì)的時序邏輯表達(dá)方法,并自動從程序中針對所有的指針變量形成相應(yīng)的時序邏輯公式.實(shí)驗(yàn)結(jié)果表明,該方法可以自動地對程序中的所有指針進(jìn)行檢測,錯誤覆蓋率高,對大規(guī)模程序的檢測有著很好的實(shí)際應(yīng)用價值.
1空指針解引用問題的LTL描述
1.1LTL
模型檢測中,一般使用時序邏輯公式描述待驗(yàn)證的性質(zhì).本文使用LTL來描述空指針解引用問題.
設(shè)AP是原子命題集合,LTL公式是由AP中的元素和操作符組成.其中,操作符包括邏輯非()、邏輯與(∧)、next(○)、until(∪)和release(R).LTL的語法定義如下:
φ∷=p|ψ|φ∧ψ|○ψ|φ∪ψ|φRψ,p∈AP.
LTL公式的語義解釋在線性結(jié)構(gòu)上.一個線性結(jié)構(gòu)是一個無限序列x=x(0),x(1),….其中,x(i)是AP到{true, false}的映射.一個LTL公式φ在線性結(jié)構(gòu)x的第i個位置滿足一個線性結(jié)構(gòu)x,記作:x,i?φ.語義定義如下:
x,i?p,如果x(i)(p)=true,p∈AP;
x,i?ψ,如果x,i?ψ;
x,i?φ∨ψ,如果x,i?φ或x,i?ψ;
x,i?○φ,如果x,i+1?φ;
x,i?φ∪ψ,如果存在j≥i,使得對于任意的
i′∈{i,i+1,…,j-1},x,i′?φ,并且x,j?ψ;
x,i?φRψ,如果對所有的j≥i,x,j?ψ,
或者存在j≥i,使得對于任意的
i′∈{i,i+1,…,j-1},x,i′?ψ,并且x,j?φ.
其它附加的邏輯操作符定義如下:
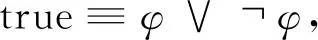
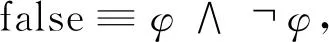
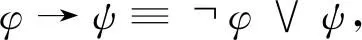
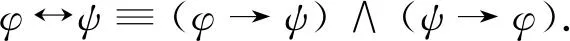
另外,時序操作符sometimes(◇)和always(□)的定義如下:
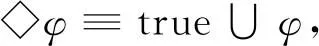
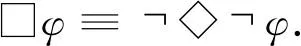
LTL公式可以表示為范式.對于一個LTL公式φ,它的范式定義為
其中,βi是狀態(tài)公式,即只包含邏輯操作符的公式;φi是一個任意的主操作符不為析取操作的LTL公式.在范式中,每一個析取項(xiàng)都代表一個遷移關(guān)系.直觀地講,范式表示存在一個整數(shù)i,βi在當(dāng)前狀態(tài)可滿足,φi在下一狀態(tài)可滿足.已證明,所有的LTL公式都可以等價地轉(zhuǎn)化為它的范式[19].
1.2LTL到TGBA的轉(zhuǎn)換
任何一個LTL公式可以被等價地轉(zhuǎn)換為一個基于遷移的廣義Büchi自動機(jī)(transition based generalized Büchi automata, TGBA)[20].為了構(gòu)造LTL公式φ的TGBA,首先創(chuàng)建初始狀態(tài)[φ],然后將φ轉(zhuǎn)換為范式.假設(shè):
φ≡(p∧r∧p∧r)∧○(φ1∧φ2)∨
p∧r∧○φ3∨p∧r∧○(φ4∧φ5),
那么可以生成3個新結(jié)點(diǎn),即[φ1∧φ2],[φ3]和[φ4∧φ5],如圖1所示:
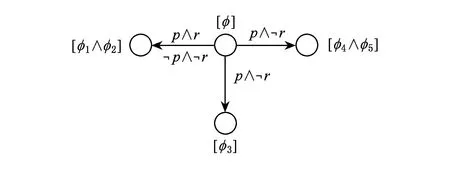
Fig. 1 Constructing TGBA.圖1 構(gòu)造TGBA
同時,生成遷移關(guān)系為
為了完成整個TGBA的構(gòu)造,需要針對每個新生成的結(jié)點(diǎn),通過將表示該結(jié)點(diǎn)的公式轉(zhuǎn)換成范式,從而不斷地產(chǎn)生新的結(jié)點(diǎn),直到?jīng)]有新的結(jié)點(diǎn)可以被生成.這樣的一個圖我們稱為φ的范式圖.
在此過程中,必須考慮一個問題:對于形如p∪q的公式,q最終要發(fā)生,即q不能被無限地延遲.但是,在范式圖中沒有顯式地體現(xiàn)出q有沒有發(fā)生.
因此,為了準(zhǔn)確地刻畫∪操作的語義,本文進(jìn)一步在范式圖的邊上增加Flag集合標(biāo)記.我們關(guān)注公式中不同的∪操作.對于每一個主操作符為∪的子式,使用一個唯一整數(shù)下標(biāo)i來區(qū)分,這里i>0.這樣,第i個∪操作,記為∪i.一個LTL公式的范式圖中,一個狀態(tài)[φ]中的所有主操作符為∪的子式所對應(yīng)的下標(biāo)構(gòu)成的整數(shù)集合稱為Untilφ.整個范式圖中,所有主操作符為∪的子式所對應(yīng)的下標(biāo)構(gòu)成的整數(shù)集合稱為AllUntil.據(jù)此,指向狀態(tài)[φ]的遷移上的標(biāo)記為Flag=AllUntilUntilφ.
對于一個LTL公式φ=p∪(q∪r),它對應(yīng)的TGBA如圖2所示,在圖2中“{}”是每一個狀態(tài)所包含的主操作符為∪的子式的整數(shù)標(biāo)記集合,“[]”是每一條遷移上的Flag集合.
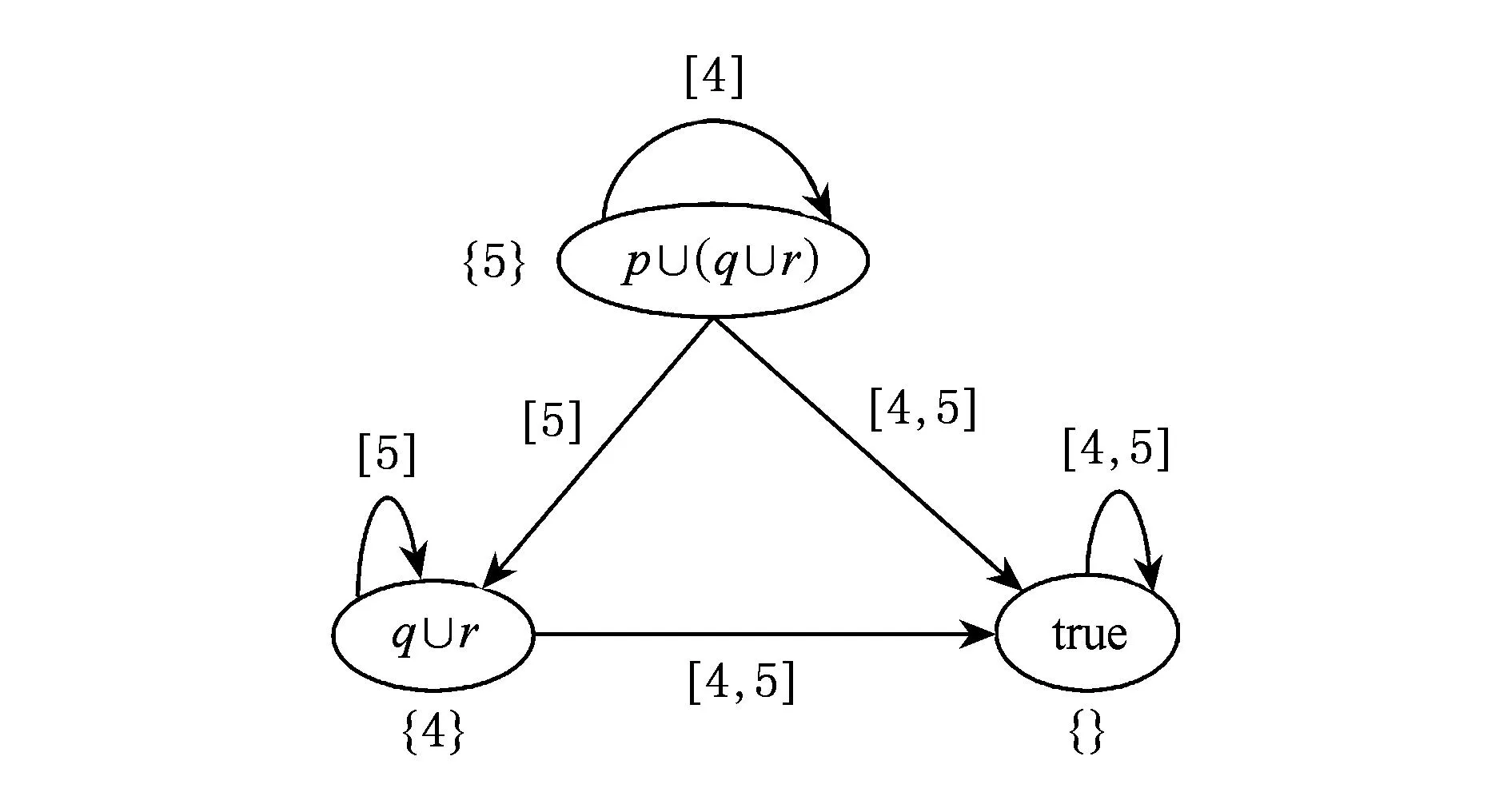
Fig. 2 TGBA of the formula φ.圖2 公式φ的TGBA.
從圖2可以看出,“q∪r”,記為φ中的主操作符∪,被標(biāo)記為4;“p∪(q∪r)”,記為φ1中的主操作符∪,被標(biāo)記為5;“true”,記為φ2,不包含∪.所以,整個TGBA的AllUntil集合為{4,5},Untilφ為{4},Untilφ1為{5},Untilφ2為{}.
范式圖以及Flag標(biāo)記構(gòu)成了與給定LTL公式等價的TGBA.TGBA上一個無窮路徑是指從初始結(jié)點(diǎn)出發(fā)的一個結(jié)點(diǎn)與邊相交互的無窮序列,π=n0,e0,n1,e1,…,(ni,ei,…,nj,ej)ω,0≤i≤j.為了方便,我們用infn(π)表示π的循環(huán)部分的結(jié)點(diǎn)集合,infe(π)表示循環(huán)部分的邊集合.一個路徑π是可接收的,當(dāng)且僅當(dāng):
AllUntil={Flag(e)|e∈infe(e)}.
1.3空指針解引用的LTL描述
空指針解引用問題指:當(dāng)程序中使用某個指針變量的解引用形式時,該指針變量為空.在該情況下會導(dǎo)致程序出錯甚至崩潰.為了使用LTL公式表示空指針解引用問題,我們首先定義2個命題:
命題1.d:表示指針p≠null.d為真當(dāng)且僅當(dāng)在當(dāng)前狀態(tài)下指針變量p≠null.
命題2.r:表示使用了指針p的解引用形式,即*p或p→.r為真當(dāng)且僅當(dāng)當(dāng)前狀態(tài)使用了指針的解引用形式.
因此,指針變量p的空指針解引用可以描述為:程序中某一時刻p=null且出現(xiàn)了對p的解引用形式.在模型檢測中,一般描述期望的性質(zhì):即該程序中不存在空指針解引用.該期望的性質(zhì)用LTL公式描述為□(r→d).
為了檢測待測程序是否滿足性質(zhì)□(r→d),理論上我們需要將□(r→d)的否定,即(□(r→d))轉(zhuǎn)換為TGBA;然后檢測程序中是否存在可能的執(zhí)行路徑與所得到的TGBA的接收路徑相吻合.
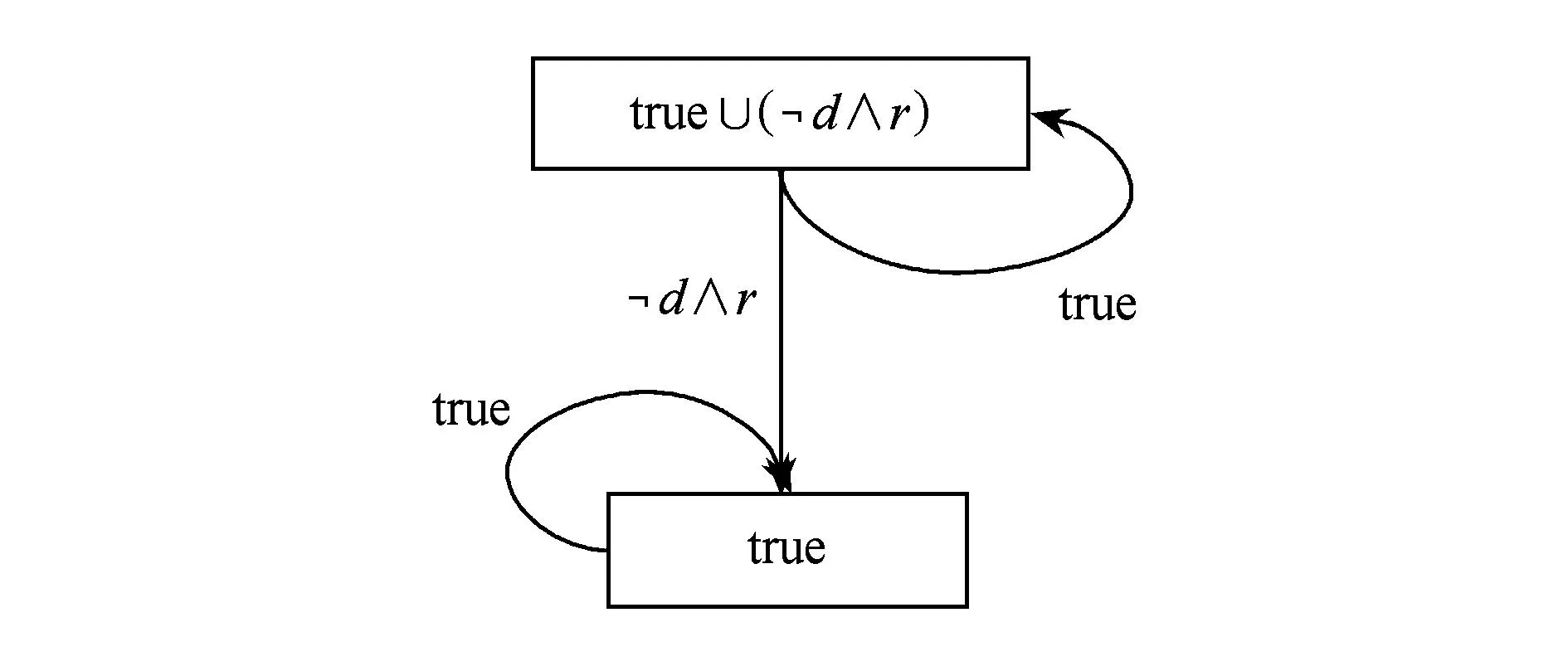
Fig. 3 TGBA of formula true∪(d∧ r).圖3 公式true∪(d∧ r)的TGBA
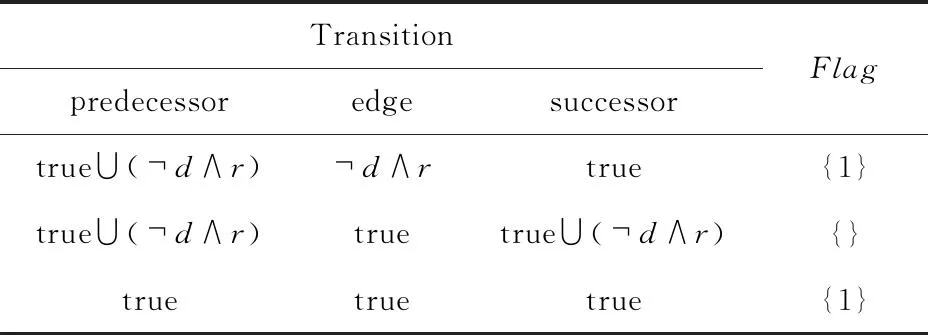
TransitionpredecessoredgesuccessorFlagtrue∪(d∧r)d∧rtrue{1}true∪(d∧r)truetrue∪(d∧r){}truetruetrue{1}
2空指針解引用性質(zhì)的LTL公式生成
如1.3節(jié)所述,程序中不存在空指針解引用的性質(zhì)可以通過LTL公式□(r→d)來描述.因此,我們可以看出,對于不同的指針變量公式是不變的.但是命題d和r的具體定義不同,它們要對應(yīng)具體的指針變量.因此,基于這種模式,本節(jié)給出了針對任意指針變量的LTL公式形式方法.
在程序中,指針變量的定義存在2種情況:1) 聲明語句,可以以全局或局部變量的形式出現(xiàn);2) 函數(shù)的形參,出現(xiàn)在函數(shù)的定義中.為了對所有的指針變量形成相應(yīng)的LTL公式,我們首先通過分析程序的語法樹,提取所有的指針變量,并記錄相關(guān)的變量名稱、類型和作用域(通過所在函數(shù)的名稱來體現(xiàn),其中全局變量略去函數(shù)名稱);然后針對不同的指針變量,例如變量v,定義命題d和r:
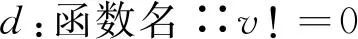
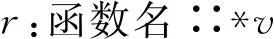
具體的指針變量的提取算法如算法1所示:
算法1. 指針變量的提取.
輸入:控制流自動機(jī)cfa、保存變量信息的集合varInfo、保存函數(shù)信息的集合funcInfo、保存類型信息的集合typeInfo;
輸出:varInfo.
① fornodeincfado*對cfa中每一個結(jié)點(diǎn)*
② ifnode是函數(shù)入口結(jié)點(diǎn)then*提取函
③paras=extractFuncInfo(node,
funcInfo);
④ forparainparasdo
⑤ ifpara是一個指針變量then
⑥extractVarInfo(para,varInfo);
⑦ end if
⑧ end for
⑨ end if
⑩edges=getLeavingEdges(node);



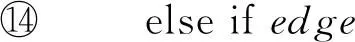





在算法1中,為了方便分析,提取指針變量時,同時記錄了所在函數(shù)和復(fù)雜類型的信息.在得到所有變量信息后,可以任意選擇一個變量,生成對應(yīng)的LTL公式進(jìn)行檢測,也可以選擇對所有變量自動地逐個形成公式并檢測.
3基于CEGAR的空指針解引用模型檢測
本節(jié)首先描述了模型檢測中使用的2種數(shù)據(jù)結(jié)構(gòu):控制流自動機(jī)(control flow antomata, CFA)和抽象可達(dá)圖(abstract reachability graph, ARG);然后,詳細(xì)地介紹了基于CEGAR的空指針解引用模型檢測方法.
3.1CFA和ARG
CFA是一個有向圖.其中,結(jié)點(diǎn)代表程序的位置,通過一個程序計數(shù)器的值來編號;邊表示的是連接2個結(jié)點(diǎn)的操作,對應(yīng)C程序的語句,包括賦值操作、分支語句、函數(shù)調(diào)用和return語句等.
一個程序的CFA可以定義為一個四元組A={L,O,lentry,lexit},其中,L是程序位置的集合;O?L×ops×L是控制流邊的結(jié)合,表示控制流2個相鄰結(jié)點(diǎn)之間執(zhí)行的操作;lentry∈L是程序的起始位置;lexit∈L是程序的終止位置.
對于CFA中的一個程序位置l∈L,l的前驅(qū)集合定義為Pre(l)={l′|(l′,ops,l)∈O},l的后繼集合定義為Succ(l)={l′|(l,ops,l′)∈O}.以下面代碼為例,它的CFA如圖4所示.
① void main(){
② inti;
③ int*p;
④ ifi<2
⑤p=&i;
⑥ end if
⑦*p=1;
⑧ }
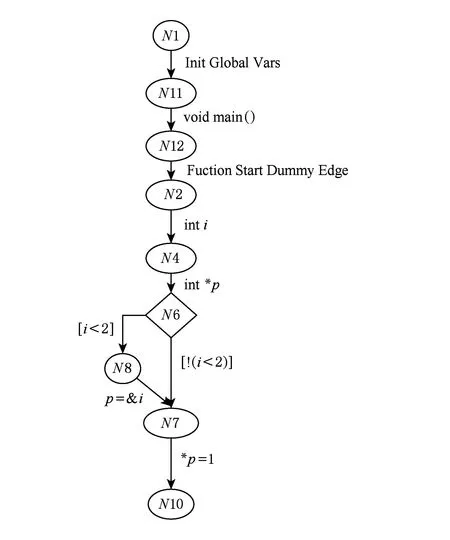
Fig. 4 CFA.圖4 控制流自動機(jī)
ARG是在考慮CFA中每個位置的謂詞真值的情況下,通過展開CFA而得到的.它表示的是程序可達(dá)的狀態(tài)空間.
給定一個程序的控制流圖A={L,O,lentry,lexit}和相關(guān)的謂詞集合Pred.該程序的ARG為一個四元組G={N,E,Ninit,Nf}.其中,N是結(jié)點(diǎn)集合,對于任意的n∈N,n=(l,Pred(l)),l∈L,Pred:L→2Pred稱為可達(dá)域,表示位置l與Pred的映射關(guān)系;E?N×ops×N是控制流邊的子集;Ninit和Nf是初始結(jié)點(diǎn)集合和終止結(jié)點(diǎn)集合.
為了方便,對于一個結(jié)點(diǎn)n=(l,Pred(l))∈N,我們用n.l表示l;用n.r表示Pred(l).如果n∈Ninit(Nf),則n.l=lentry(lexit).
實(shí)際上,ARG是程序的抽象模型,其中一條路徑對應(yīng)于程序的一次執(zhí)行.一個結(jié)點(diǎn)n的可達(dá)域(n.r)表示假設(shè)程序沿著一個操作序列執(zhí)行,從起始結(jié)點(diǎn)到結(jié)點(diǎn)n得到的可達(dá)狀態(tài)的近似集合.因此,考慮的謂詞越少,ARG就越小,驗(yàn)證的效率越高.一個CFA可以看成一個特殊的ARG,其中,所有結(jié)點(diǎn)的可達(dá)域都為空.但是在ARG中,一條不滿足期望性質(zhì)的路徑可能在實(shí)際程序中不存在.然而,基于CEGAR的懶惰抽象(lazy abstraction)[21]方法可以通過插值得到更多的謂詞,從而有效地消除虛假反例.
3.2基于CEGAR的C程序空指針解引用檢測
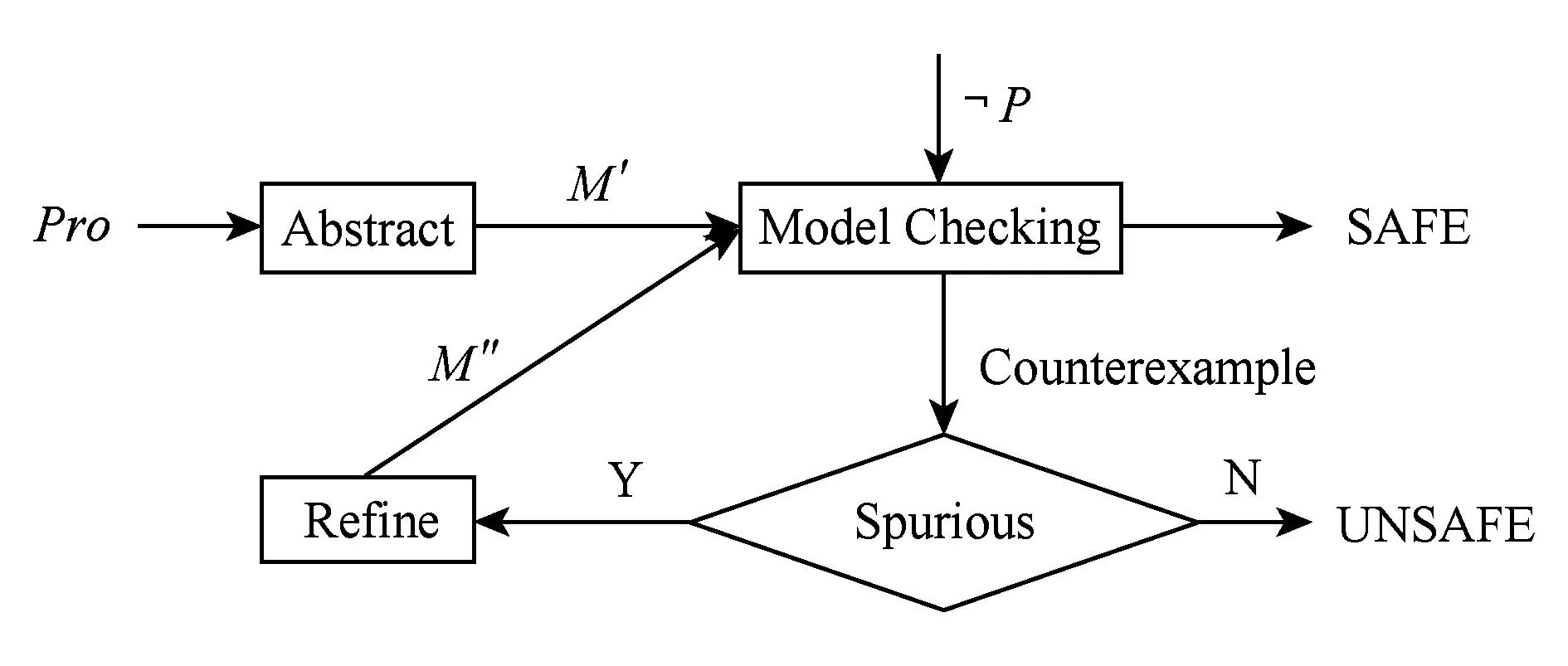
Fig. 5 Framework of CEGAR based model checking.圖5 基于CEGAR的模型檢測整體框架
基于CEGAR的C程序空指針解引用模型檢測的整體框架如圖5所示.1)使用LTL公式P描述期望的性質(zhì),即程序中不存在空指針解引用問題;2)檢測程序是否可以滿足P的否定.如果可以滿足,那么程序中存在可能的執(zhí)行路徑與期望的性質(zhì)相違背,否則程序滿足期望的性質(zhì).程序的狀態(tài)空間往往非常大,甚至無窮大,因此,本文使用謂詞抽象的方法得到程序的一個抽象模型.在初始的抽象模型中,僅關(guān)心與性質(zhì)P相關(guān)的所有謂詞.如圖5所示,通過抽象我們從待測程序Pro得到它的抽象模型M′;然后檢測M′是否可以滿足性質(zhì)的否定,即P.若M′的所有路徑都不能滿足P,可以給出結(jié)論:程序Pro中沒有空指針解引用發(fā)生;反之,如果在M′中找到一條路徑可以滿足P,需要進(jìn)一步檢測該路徑的真實(shí)性,即該路徑是否在源程序中存在.若該路徑是真實(shí)存在的路徑,那么我們找到了程序中的一個空指針解引用錯誤;否則,如果該路徑是虛假的,需要進(jìn)一步通過添加新的謂詞來對M′進(jìn)行細(xì)化.重復(fù)以上過程,直到發(fā)現(xiàn)一個錯誤,或者證明程序中沒有錯誤為止.在CPAChecker的CEGAR算法中,細(xì)化操作是通過調(diào)用SMT求解器來完成的,它將一條反例路徑轉(zhuǎn)化為SMT求解器可處理的公式序列,然后通過求解器來求解.新的謂詞是通過Craig差值[22]算法得到的.
本文的算法是在現(xiàn)有的軟件模型檢測工具CPAChecker的基礎(chǔ)上實(shí)現(xiàn).CPAChecker自身不能支持時序邏輯性質(zhì)的檢測,它需要首先在程序中對待檢測的問題進(jìn)行插樁,然后使用上述CEGAR循環(huán)進(jìn)行檢測.通過插樁的方式,只需要對能到達(dá)插樁的位置的路徑進(jìn)行檢測,從這個角度看,插樁的方法隱式地縮小檢測范圍,在一定程度上對檢測路徑進(jìn)行了篩選,而且,如果程序中有錯誤,那么錯誤肯定在插樁的位置,方便定位錯誤.CEGAR算法檢測流程圖如圖6所示.在圖6中,首先讀入插樁后的C程序,并生成程序的CFA;然后根據(jù)插樁信息,展開CFA,提取謂詞,生成ARG.如果錯誤標(biāo)簽不可達(dá),即不存在反例路徑(counterexample, CE),說明程序安全;否則需判斷反例路徑是否虛假.如果反例路徑是虛假的,說明考慮的謂詞太少,需要提取新的謂詞進(jìn)一步細(xì)化,然后繼續(xù)檢測;如果反例路徑不是虛假的,則說明程序不安全,輸出反例路徑.
Fig. 6 Flow diagram of the CEGAR algorithm in CPAChecker.圖6 CPAChecker中CEGAR算法的流程圖
3.3on-the-fly檢測
為了緩解驗(yàn)證過程中的狀態(tài)空間,本文結(jié)合CFA和LTL性質(zhì),采用on-the-fly的方式逐步生成ARG,同時對性質(zhì)進(jìn)行檢測.
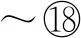
算法2.LTLModelCheck(M,V).
輸入:帶驗(yàn)證的程序M、待檢測的指針變量V;
輸出:true或false.
①target=null,success=false;
②M→cfa;*生成CFA*
③AP=generate(V),P=Property(AP);
④S0=initARGState(cfa,AP,P);*初始狀態(tài)*
⑤reached={S0};*可達(dá)狀態(tài)集合*
⑥waitlist={S0};*一個棧,存放未處理的狀態(tài)*
⑦AllUntil=LTL2NF(P);
⑧ do{
⑨t(yī)arget=generateARG(cfa,reached,
waitlist,AllUntil);
⑩ iftarget!=null then






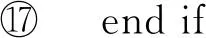


算法3.generateARG(cfa,reached,waitlist,AllUntil).
輸入:控制流自動機(jī)cfa、可達(dá)狀態(tài)集合reached、用來存放未處理狀態(tài)的一個棧waitlist、待驗(yàn)證性質(zhì)對應(yīng)的AlLUntil集合AllUntil;
輸出:1個ARGState.
① whilewaitlist!=null do
②s=getTopWaitlist(),p=P(s);
③TR=nextStateNF(s,p);
④ ifTR=null then goto ③;
⑤ forT′ inTRdo
⑥sucs=computeSucs(s,cfa) ;*后繼狀
⑦ ifsucs==null then
⑧ ifexistCE(reached,s,AllUntil) then
⑨ returns;
⑩ end if
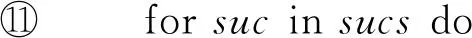



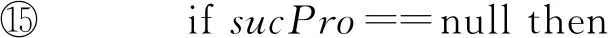



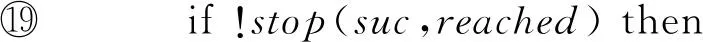


then
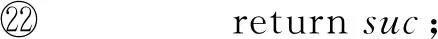

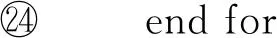
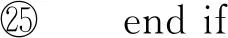


在算法3中,語句p=P(s)計算狀態(tài)s的性質(zhì)集合;函數(shù)stop判斷后繼狀態(tài)suc是否被覆蓋;函數(shù)getSucProperty計算后繼狀態(tài)滿足的性質(zhì);函數(shù)CP計算后繼狀態(tài)需要滿足的命題;函數(shù)existCE判斷是否存在反例路徑.函數(shù)getSucProperty的計算過程如算法4所示.
算法4.getSucProperty(S,T).
輸入:1個ARG狀態(tài)S、性質(zhì)的1條遷移T;
輸出:S的后繼狀態(tài)滿足的性質(zhì).
①M(fèi)=S.getPropositions();*狀態(tài)S滿足的命題集合*
②booleanbool=true;
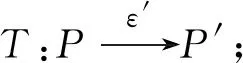
④ forminMdo*對M中每一個命題*
⑤ ifm∧ε′ !=false then
⑥ continue;
⑦ else
⑧bool=false;
⑨ break;
⑩ end if





算法4中,T為遷移關(guān)系,ε′代表的是遷移關(guān)系T的接受條件.如果命題集合M中的每一個命題與ε′的交集都不為空,則說明狀態(tài)S滿足性質(zhì)P′.
函數(shù)CP的計算方法如下:1) 求出初始狀態(tài)到S的路徑,記作path.2)將path轉(zhuǎn)為SMT能夠接受的形式,記作pathformula.3)得到前驅(qū)狀態(tài)的命題集合pp.4) 對集合pp中的命題d,做如下操作:將命題d轉(zhuǎn)為SMT公式f,加入pathformula,并用SMT求解.如果結(jié)果為true,則說明S狀態(tài)滿足命題d;否則,S狀態(tài)不滿足命題d,即滿足d的否定.對于命題r,則通過分析對應(yīng)的c表達(dá)式來判斷其是否可滿足.
函數(shù)existCE的計算過程如算法5所示.其中,path為從初始狀態(tài)到達(dá)輸入狀態(tài)E的路徑.反例路徑是根據(jù)path的循環(huán)部分來判斷.
算法5.existCE(reached,E,AllUntil).
輸入:可達(dá)狀態(tài)集合reached、一個ARG狀態(tài)E、待驗(yàn)證性質(zhì)對應(yīng)的AlLUntil集合AllUntil;
輸出:true或false.
①path=getPath(reached,E);
② foreinpathdo
③Flag=getFlag(e);*計算Flag集合*
④ foriinFlagdo
⑤Fi=Fi∪{e};
⑥ end for
⑦ end for
⑧ foriinAllUntildo
⑨ ifFi∧path!=null then
⑩ continue;





4實(shí)驗(yàn)結(jié)果分析
為了驗(yàn)證本文提出的方法,我們在CPAChecker的基礎(chǔ)上開發(fā)了C程序空指針解引用檢測工具NULPChecker,并通過程序驗(yàn)證Benchmark程序*https:svn.sosy-lab.orgsoftwaresv-benchmarkstagssvcomp14對工具的效果進(jìn)行評估.
4.1工具實(shí)現(xiàn)
本文在現(xiàn)有CPAChecker的基礎(chǔ)上,利用謂詞抽象、CEGAR、on-the-fly以及時序邏輯等開發(fā)了C程序空指針解引用檢測工具:NULPChecker.圖7給出了該工具的主要框架.CFA模塊是基于Eclipse平臺的插件,它根據(jù)C程序的語法樹生成程序的CFA,同時,變量提取模塊通過分析CFA提取指針變量.LTL模塊根據(jù)變量提取模塊提取的變量,生成LTL公式,將LTL公式轉(zhuǎn)為與其等價的TGBA,然后和ARG模塊進(jìn)行交互.ARG模塊利用on-the-fly的思想,逐步展開CFA和LTL公式,在展開的同時,檢查CFA當(dāng)前狀態(tài)的命題與公式范式的當(dāng)前狀態(tài)是否沖突.重復(fù)此過程,直到不再產(chǎn)生新的狀態(tài).在沒有沖突出現(xiàn)時產(chǎn)生的一條完整路徑對應(yīng)一條反例路徑,該路徑是否真實(shí)存在還需進(jìn)一步判斷.細(xì)化模塊首先利用SMT求解器判斷反例的真實(shí)性,如果反例路徑是虛假的,則采用插值的方法提取新的謂詞,重復(fù)上述過程直到給出真反例或證明程序正確.輸出模塊輸出程序的驗(yàn)證結(jié)果,驗(yàn)證過程中,可以選擇“單個指針”和“所有指針”.
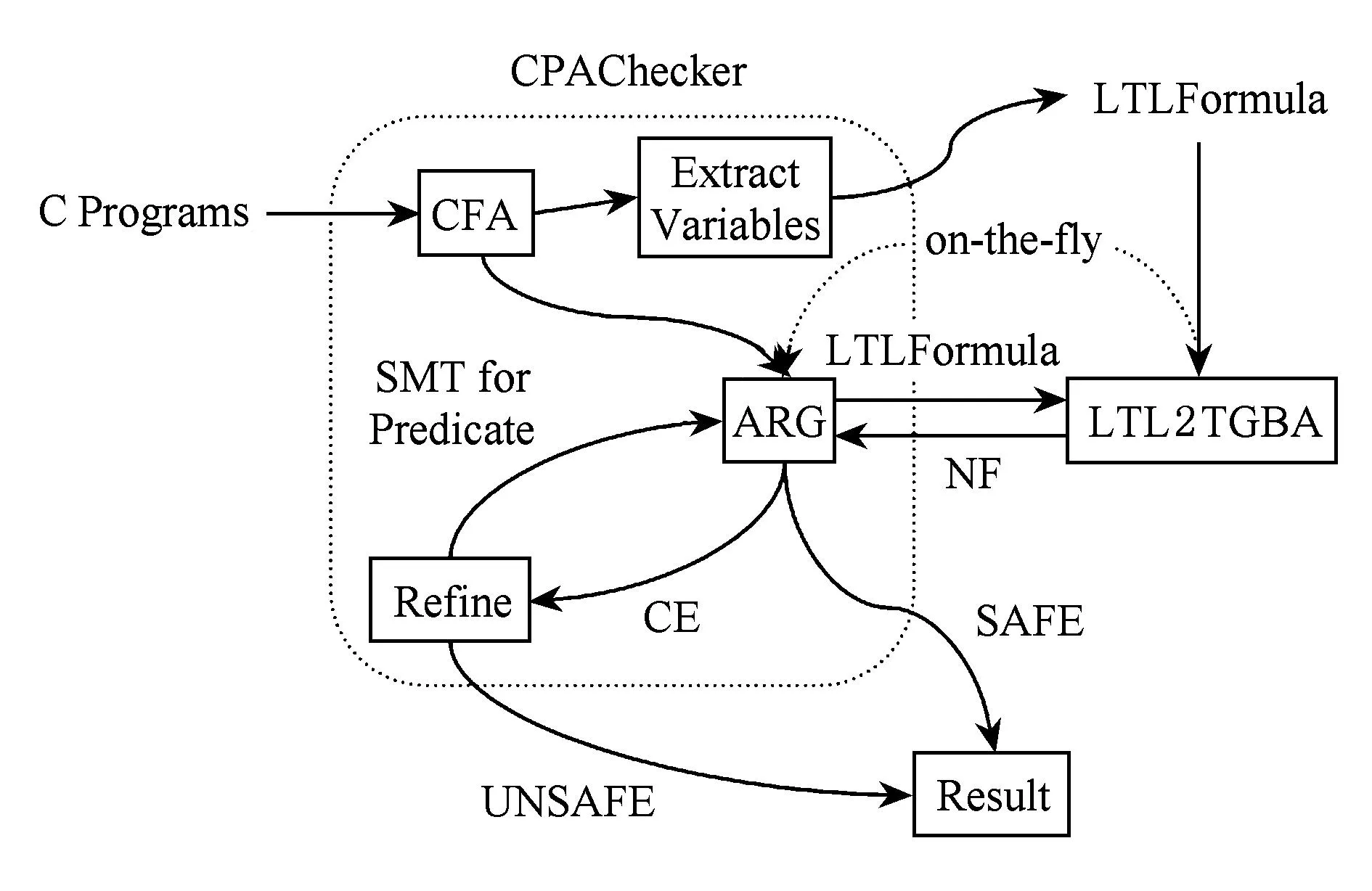
Fig. 7 Core of NULPChecker圖7 NULPChecker的中心結(jié)構(gòu)
我們使用NULPChecker檢測第3節(jié)中的程序中是否存在空指針解引用問題.在檢測過程中,工具提示程序中存在一個指針變量,如圖8所示,我們選擇檢測指針變量p是否存在空指針解引用現(xiàn)象.檢測結(jié)束后,工具提示存在錯誤路徑,如圖9所示.
Fig. 8 Choosing pointer.圖8 指針選擇
4.2實(shí)驗(yàn)結(jié)果
本文通過NULPChecker檢測了程序驗(yàn)證Benchmark程序中的空指針解引用問題,檢測結(jié)果如表2所示.表2中,列1顯示的是測試程序名,列2是程序的行數(shù),列3是程序中指針變量的總數(shù),列4是驗(yàn)證結(jié)果安全的指針變量總數(shù),列5是出現(xiàn)空指針解引用問題的指針變量總數(shù).
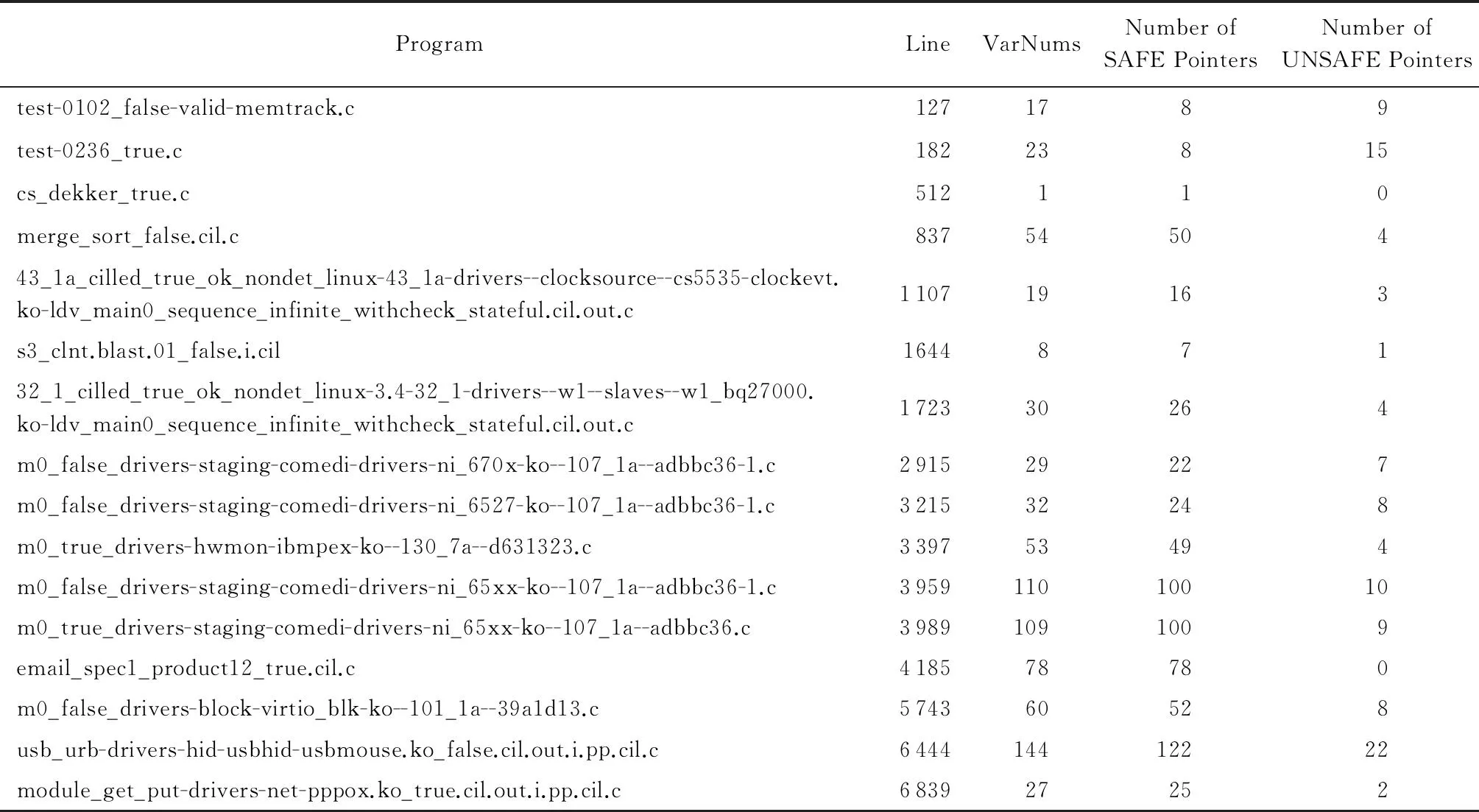
Table 2 Experimental Data
這里需要指出的是,CPAChecker只支持對加錯誤標(biāo)簽的位置進(jìn)行檢查,因此,要檢查一個指針的所有使用情況,則需要手動地加入很多標(biāo)簽.如果要檢測所有的指針,不能保證能夠準(zhǔn)確地在所有的位置加上合適的標(biāo)簽,而本文的方法無需手動對程序作任何修改.NULPChecker支持對任意C程序中所有空指針解引用的全自動檢測,無需人工干預(yù).
5結(jié)束語
本文提出了全自動的基于CEGAR的C程序空指針解引用檢測方法,并開發(fā)了相應(yīng)的支撐工具.本文的貢獻(xiàn)在于指出了程序中常見錯誤的基于LTL的驗(yàn)證模式.本文針對的是C程序中的空指針解引用問題,但是,所提出的方法也可以用來檢測其它問題,如數(shù)組越界、除零問題等,這也是本文的后期研究工作.本文給出的模型檢測算法目前已經(jīng)可以對空指針解引用問題進(jìn)行檢測,但是還存在許多缺陷.如果程序存在循環(huán)結(jié)構(gòu),可能會展開多次,最終系統(tǒng)內(nèi)存不足使程序停止.在分析結(jié)構(gòu)體指針或數(shù)組等涉及內(nèi)存操作的變量時,對變量信息的提取和分析不夠完整,會導(dǎo)致程序誤報或漏報.程序?qū)語言的一些復(fù)雜的語法結(jié)構(gòu)的支持還不夠完善,而且調(diào)用的系統(tǒng)函數(shù)不能識別其作用,也會導(dǎo)致程序分析結(jié)果錯誤.檢查的程序規(guī)模雖然有所提高,但是跟待測程序的設(shè)計結(jié)構(gòu)有很大關(guān)系.有時程序的規(guī)模不是很大,但函數(shù)之間的調(diào)用關(guān)系可能會很復(fù)雜,如出現(xiàn)遞歸調(diào)用或者循環(huán)體的循環(huán)次數(shù)太大而導(dǎo)致程序堆棧和堆不夠用.算法本身會保存很多信息來分析程序,這會占用大量內(nèi)存.這些問題在后續(xù)的研究中都要進(jìn)行分析.
參考文獻(xiàn)
[1]Xiao Qing, Gong Yunzhan, Yang Chaohong, et al. Path sensitive static defect detecting method[J]. Journal of Software, 2010, 21(2): 209-217 (in Chinese)(肖慶, 宮云戰(zhàn), 楊朝紅, 等. 一種路徑敏感的靜態(tài)缺陷檢測方法[J]. 軟件學(xué)報, 2010, 21(2): 209-217)
[2]Shapiro M, Horwitz S. Fast and accurate flow-insensitive points-to analysis[C]Pror of the 24th ACM Symp on Principles of Programming Languages. New York: ACM, 1997: 1-14
[3]Ben H, Lin C. Semi-sparse flow-sensitive pointer analysis[J]. SIGPLAN Notices, 2009, 44(1): 226-238
[4]Dalley James L. The art of software testing[C]Proc of National Aerospace and Electronics Conf. Piscataway, NJ: IEEE, 1991: 757-760
[5]Repasi T. Software testing-state of the art and current research challenges[C]Pror of the 5th Int Symp on Applied Computational Intelligence and Informatics. Piscataway, NJ: IEEE, 2009: 47-50
[6]Ellis B J, Ireland A. An integration of program analysis and automated theorem proving[C]Proc of the 4th Int Conf on Integrated Formal Methods. Berlin: Springer, 2004: 67-86
[7]Clarke E M, Grumberg O, Long D E. Model checking and abstraction[J]. ACM Trans on Programming Languages and Systems, 1994, 16(5): 1512-1542
[8]Jhala R, Rupak M. Software model checking[J]. ACM Computing Surveys, 2009, 41(4): 1-21
[9]Beyer D, Henzinger T A, Jhala R, et al. The software model checker Blast: Applications to software engineering[J]. International Journal on Software Tools for Technology Transfer, 2007, 9(56): 505-525
[10]Bayer D, Henzinger T A, Jhala R, et al. Checking memory safety with Blast[C]Pror of the 8th Int Conf on FASE. Berlin: Springer, 2005: 2-18
[11]Condit J, Harren M, McPeak S, et al. CCURED in the real world[C]Proc of SIGPLAN Notices. New York: ACM, 2003: 232-244
[12]Beyer D, Keremoglu M E. CPACHECKER: A tool for configurable software verification[C]Proc of the 23rd Int Conf on Computer Aided Verification. Berlin: Springer, 2011: 184-190
[13]Bayer D, Henzinger T A, Theoduloz G. Configurable software verification: Concretizing the convergence of model checking and program analysis[C]Proc of the 19th Int Conf on Computer Aided Verification. Berlin: Springer, 2007: 504-518
[14]Clarke E M, Kroening D, Lerda F. A tool for checking ANSI-C programs[C]Proc of the 10th Int Conf on Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2004: 168-176
[15]Charatonik W, Georgieva L, Maier P. Bounded model checking of pointer programs[C]Proc of the 19th Int Workshop on Computer Science Logic. Berlin: Springer, 2005: 397-412
[16]Frazan A, Madhusudan P, Razavi N, et al. Predicting null-pointer dereferences in concurrent programs[C]Proc of the
20th ACM SIGSOFT Int Symp on the Foundations of Software Engineering. New York: ACM, 2012: 47-57
[17]Dong Yukun, Gong Yunzhan, Jin Dahai. Null pointer dereference defect detecting based on region-based memory model[J]. Acta Electronica Sinica, 2014, 42(9): 1744-1752 (in Chinese)(董玉坤, 宮云戰(zhàn), 金大海. 基于區(qū)域內(nèi)存模型的空指針引用缺陷檢測[J]. 電子學(xué)報, 2014, 42(9): 1744-1752)
[18]Clarke E. Counterexample-guided abstraction refinement[C]Proc of the 10th Int Symp on Temporal Representation and Reasoning and the 4th Int Conf on Temporal Logic. Piscataway, NJ: IEEE, 2003: 154-169
[19]Tian Cong, Duan Zhenhua. A note on stutter-invariant PLTL[J]. Information Processing Letters, 2009, 109(13): 663-667
[20]Gastin P, Oddoux D. Fast LTL to Büchi automata translation[C]Proc of the 13th Int Conf on Computer Aided Verification. Berlin: Springer, 2012: 53-65
[21]McMillan K L. Lazy abstraction with interpolants[C]Proc of the 18th Int Conf on Computer Aided Verification. Berlin: Springer, 2006: 123-136
[22]Henzinger T A, Jhala R, Majumdar R. Abstractions from proofs[C]Pror of the 31st ACM SIGPLAN-SIGACT Symp on Principles of Programming Languages. New York: ACM, 2004: 232-244

Duan Zhao, born in 1990. Received his MS degree from the Institute of Computing Theory and Technology, Xidian Universiy, Xi’an, in 2015. PhD candidate. His main research interests include software model checking and program analysis.

Tian Cong, born in 1981. Professor and PhD supervisor in the Institute of Computing Theory and Technology, Xidian University. Member of IEEE.Her main research interests include theories in model checking, temporal logics and automata, formal verification of software systems, and software engineering.

Duan Zhenhua, born in 1948. Professor and PhD supervisor in the Institute of Computing Theory and Technology, Xidian University. Senior member of IEEE. His main research interests include model checking, temporal logics, formal verification of software systems, and temporal logic programming.
中圖法分類號TP31
基金項(xiàng)目:國家自然科學(xué)基金項(xiàng)目(61322202,61420106004,91418201,61133001,61272117)
收稿日期:2015-07-20;修回日期:2015-10-16
This work was supported by the National Natural Science Foundation of China (61322202,61420106004,91418201,61133001,61272117).

