基于MP-PIC方法的泥沙靜水沉降三維數(shù)值模擬研究

楊海龍，張慶河，謝 琳

(天津大學(xué) 水利工程仿真與安全國家重點(diǎn)實(shí)驗(yàn)室，天津 300072)

傳統(tǒng)泥沙運(yùn)動(dòng)力學(xué)主要是通過各種推移質(zhì)、懸移質(zhì)輸沙公式或方程來描述泥沙輸移和地形演變[1-2]，對局部沖刷等較為劇烈的泥沙運(yùn)動(dòng)進(jìn)行數(shù)值模擬研究，大多也是將床面剪切應(yīng)力作為泥沙起動(dòng)的主要?jiǎng)恿σ蛩兀⑵漶詈系侥嗌硾_淤模型中，無法揭示水流泥沙運(yùn)動(dòng)的內(nèi)在機(jī)制[3]。近年來，隨著計(jì)算機(jī)計(jì)算能力的提高，從細(xì)觀尺度研究泥沙運(yùn)動(dòng)規(guī)律的工作越來越多，例如，以DPM(Discrete Particle Method)為代表的離散顆粒模型，能夠通過對單個(gè)顆粒運(yùn)動(dòng)進(jìn)行模擬來分析水流泥沙相互作用機(jī)理[4]。DPM方法可以描述顆粒運(yùn)動(dòng)過程，模擬精度較高，但存在計(jì)算量巨大，目前只能模擬顆粒數(shù)為幾萬或者幾十萬級(jí)的問題，而對于百萬甚至千萬級(jí)的大規(guī)模顆粒運(yùn)動(dòng)還很難滿足計(jì)算要求，將其應(yīng)用于模擬實(shí)際的工程問題尚存在困難。

MP-PIC(MultiPhase Particle-In-Cell)稱為多相流質(zhì)點(diǎn)網(wǎng)格模型[5]，是一種新型的離散顆粒模擬方法，近年來在化工等領(lǐng)域得到了廣泛應(yīng)用。與傳統(tǒng)的DPM方法不同，該方法將離散的顆粒碰撞力視為一個(gè)連續(xù)的各向同性的顆粒相應(yīng)力梯度力場，該梯度應(yīng)力的大小與顆粒體積分?jǐn)?shù)密切相關(guān)，在實(shí)際計(jì)算過程中不需要進(jìn)行顆粒鄰域搜索，無須計(jì)算顆粒間的接觸力。另外，該模型可以采用一個(gè)“代表顆粒”來代表具有相同動(dòng)力學(xué)特性的顆粒群，因此能夠極大地節(jié)省計(jì)算量，提高顆粒模擬的計(jì)算效率，適用于模擬百萬甚至千萬級(jí)的大規(guī)模的顆粒系統(tǒng)[6]，有望應(yīng)用于實(shí)際工程問題的模擬。為此，本文將基于MP-PIC方法，采用歐拉方法描述液相，用拉格朗日法描述顆粒相運(yùn)動(dòng)，建立描述泥沙靜水沉降的三維數(shù)值模型，并采用該模型對泥沙靜水沉降進(jìn)行模擬研究。

1 模型的建立與計(jì)算方法

1.1 流體控制方程及拖曳力模型

1.1.1 流體運(yùn)動(dòng)控制方程

MP-PIC模型中，考慮顆粒組分影響的三維流體運(yùn)動(dòng)的控制方程由以下兩相流連續(xù)性方程和時(shí)均Navier-Stokes方程組成[7]

(1)

(2)

(3)

式中：f為計(jì)算顆粒運(yùn)動(dòng)函數(shù)；mp為顆粒質(zhì)量；up為顆粒運(yùn)動(dòng)速度；uf為顆粒位置處的流體速度；Dp為拖曳力系數(shù)；P為顆粒位置處的流體壓力梯度；ρp為顆粒密度。

1.1.2 紊流模型

為了使式(3)在求解時(shí)封閉，需要引入描述紊動(dòng)粘性系數(shù)μt的紊流模型。MP-PIC模型采用了大渦模擬(LES)，它是介于直接數(shù)值模擬(DNS)與雷諾平均法(RANS)之間的一種紊流數(shù)學(xué)模型。此方法通過濾波函數(shù)將紊流運(yùn)動(dòng)中小尺度的渦動(dòng)濾掉，而小尺度渦對大渦的影響則通過向方程中加入亞格子尺度模型(SGS)進(jìn)行描述。本文采用Samgorinsky[8]提出的SGS模型，其μt系數(shù)如下

(4)

Cs=Cs0(1-ey+/A+)

(5)

△=(δxδyδz)1/3

(6)

式中：Cs為Samgorinsky常數(shù)；△為亞格子過濾尺寸；Cs0=0.1為Van Driest常數(shù)[9]；y+是到壁面無量綱化的最近距離；A+=25.0是半經(jīng)驗(yàn)化的常數(shù)；δi表示沿i軸方向的網(wǎng)格尺度。

1.1.3 拖曳力模型

本文采用由Gidaspow[10]提出的Wen-Yu[11]與Ergun[12]混合拖曳力模型，該模型由各分段函數(shù)組成，公式如下

(7)

本文中，αcp是堆積狀態(tài)下的顆粒體積分?jǐn)?shù)，一般取0.6，αp為沉降過程中的顆粒體積分?jǐn)?shù)，D1為Wen-Yu拖曳力模型，D2為Ergun模型，公式如下

(8)

(9)

式中：C1=180；C2=2；Cd為Wen-Yu拖曳力系數(shù)；rp為顆粒半徑；uf為顆粒位置處流體的流速。

(10)

(11)

1.2 顆粒運(yùn)動(dòng)方程及數(shù)值求解

1.2.1 顆粒運(yùn)動(dòng)方程

在MP-PIC方法中，固相采用離散顆粒方法，考慮顆粒的拖曳力、重力、顆粒相互碰撞的接觸力等。顆粒相的運(yùn)動(dòng)通過求解關(guān)于顆粒分布函數(shù)(PDF)f的Liouville輸運(yùn)方程[13]得到。由于顆粒不存在化學(xué)反應(yīng)，故在這里并不考慮顆粒的溫度和材料的變化。其中，f為顆粒空間位置xp、速度up、質(zhì)量mp以及時(shí)間t的函數(shù)

f=f(xp,up,mp,t)

(12)

f的輸運(yùn)方程源自于氣體動(dòng)力學(xué)理論中對碰撞項(xiàng)松弛時(shí)間有所改進(jìn)的Boltzmann-BGK方程[14-15]

(13)

(14)

式中：Ap為顆粒加速度；up為顆粒速度散度；為碰撞源項(xiàng)，由碰撞阻尼力和恢復(fù)各向同性力兩部分組成；fD和fG分別是速度為質(zhì)量平均態(tài)和高斯分布態(tài)的顆粒分布函數(shù)；τD和τG為達(dá)到這兩種局部平衡態(tài)的顆粒碰撞松弛時(shí)間，與顆粒的碰撞恢復(fù)系數(shù)有關(guān)。由此得出，顆粒運(yùn)動(dòng)方程為

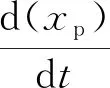
(15)

(16)

式中：Xp為顆粒碰撞力，其表達(dá)式為

(17)

(18)

αp+αf=1

(19)

式(16)中右邊第一項(xiàng)為運(yùn)動(dòng)狀態(tài)下初始碰撞力，第二項(xiàng)為顆粒堆積狀態(tài)下的平均碰撞力，只有當(dāng)顆粒出現(xiàn)堆積狀態(tài)時(shí)，該項(xiàng)才會(huì)生效。τp為顆粒碰撞正應(yīng)力，是顆粒周圍的多個(gè)顆粒對其的共同作用力，由歐拉網(wǎng)格計(jì)算得到的空間梯度應(yīng)力來表征，而梯度應(yīng)力通過插值到網(wǎng)格單元的顆粒體積分?jǐn)?shù)得到

(20)

式中：Ps為常數(shù)，是模型的參數(shù)，具有壓力的量綱；αp是顆粒的體積分?jǐn)?shù)；αcp為顆粒堆積臨界體積分?jǐn)?shù)；β和ε為無量綱常數(shù)，一般建議取2≤β≤5，ε取10-7量級(jí)的小數(shù)。由于顆粒的堆積狀態(tài)與顆粒的尺寸、形狀及排列方式有關(guān)，該模型允許顆粒的體積分?jǐn)?shù)達(dá)到或偶然超過臨界體積分?jǐn)?shù)，所以引入ε用來消除奇點(diǎn)，以保證顆粒碰撞應(yīng)力的求解不受影響。

1.2.2 顆粒與壁面間的相互作用

在MP-PIC方法中，顆粒與壁面間的相互作用并不需要對顆粒的受力進(jìn)行分析，而是引入2個(gè)系數(shù)[16]，分別為顆粒與壁面碰撞的正向恢復(fù)系數(shù)en,w和切向恢復(fù)系數(shù)et,w，由此得出顆粒與壁面碰撞后的運(yùn)動(dòng)軌跡。

uc,i,n,post=-en,w×uc,i,n,pre

(21)

uc,i,t,post=-et,w×uc,i,t,pre

(22)

式中：uc,i,n,pre和uc,i,n,post是碰撞前后的法向速度；uc,i,t,pre和uc,i,t,post是碰撞前后的切向速度，下標(biāo)i表示一個(gè)計(jì)算顆粒。

1.2.3 顆粒運(yùn)動(dòng)的數(shù)值求解

在數(shù)值計(jì)算中，流體的三維連續(xù)控制方程采用有限體積法求解，顆粒的運(yùn)動(dòng)并不是直接求解Liouville輸運(yùn)方程，而是將顆粒的性質(zhì)插值到計(jì)算網(wǎng)格單元中心，或者通過交錯(cuò)的標(biāo)量與動(dòng)量節(jié)點(diǎn)將流場的性質(zhì)插值到顆粒位置處，使得流體與顆粒的控制方程通過動(dòng)量交換隱性地耦合到一起，進(jìn)而通過有限差分的方法求得代表顆粒的位置和速度并不斷更新[17]

(23)

(24)

圖1 顆粒與流體運(yùn)動(dòng)的耦合過程Fig.1 Procedure for coupling of particles and fluid

1.3 顆粒與流體運(yùn)動(dòng)的耦合

本文采用交錯(cuò)網(wǎng)格，并通過插值算子將顆粒的屬性插值到歐拉網(wǎng)格當(dāng)中，首先求解顆粒與流體之間的動(dòng)量交換項(xiàng)，然后流體運(yùn)動(dòng)采用OpenFOAM中基于PISO算法的瞬態(tài)不可壓縮流體求解器進(jìn)行求解，再次應(yīng)用插值算法將流場的特性插回到顆粒位置處，最后求解顆粒的運(yùn)動(dòng)方程，從而實(shí)現(xiàn)顆粒與流體運(yùn)動(dòng)的耦合。具體計(jì)算過程如圖1所示。

2 顆粒沉降模擬的網(wǎng)格敏感性分析

在應(yīng)用MP-PIC方法進(jìn)行顆粒靜水沉降模擬之前，本節(jié)首先通過模擬單個(gè)顆粒泥沙在靜止水體中自由沉降過程，將顆粒沉速結(jié)果與經(jīng)驗(yàn)公式對比并進(jìn)行分析，討論模型對計(jì)算單元網(wǎng)格的敏感性，并對網(wǎng)格尺度的選取范圍給出合理建議。

2.1 幾何模型及計(jì)算參數(shù)

表1 模型中顆粒與流體參數(shù)Tab.1 Particle and fluid parameters used for the present simulation

本節(jié)采用與蘇東升[18]基于DPM方法進(jìn)行顆粒沉降模擬一樣的算例設(shè)置，模擬區(qū)域?yàn)殚L方體，坐標(biāo)原點(diǎn)位于模擬區(qū)域底邊界，z軸為高度方向，計(jì)算網(wǎng)格采用三維正方體結(jié)構(gòu)化網(wǎng)格。模擬初始時(shí)刻，顆粒位于模擬區(qū)域中軸線上，距底面一定距離從靜止?fàn)顟B(tài)釋放，流體初始時(shí)刻保持靜止，流速為零。開始階段，泥沙顆粒在重力作用下加速下沉，隨著顆粒速度不斷增大，顆粒所受拖曳力不斷增大，顆粒做加速度不斷減小的變加速運(yùn)動(dòng)，當(dāng)顆粒所受的拖曳力與重力保持平衡時(shí)，達(dá)到穩(wěn)定沉降速度并保持勻速下沉。在模擬中要保證顆粒達(dá)到沉降速度時(shí)與計(jì)算底面仍有足夠的高度，與x軸和y軸方向壁面擁有足夠的寬度，排除模型壁面對顆粒沉速的影響。模擬中，顆粒形狀簡化為球體，本節(jié)選取顆粒直徑為0.1 mm和2 mm兩組算例，每一組算例分別設(shè)置計(jì)算網(wǎng)格長度Δx與顆粒直徑D的比例為2、5、10、20、40五種情況，共計(jì)10個(gè)算例。其中，粒徑為0.1 mm的算例采用層流模型，粒徑為2 mm的算例采用LES紊流模型。當(dāng)Δx/D小于40時(shí)，計(jì)算域長度和寬度均取為顆粒粒徑的100倍，高度取為粒徑的500倍，當(dāng)Δx/D等于40時(shí)，計(jì)算域長度和寬度均取為顆粒粒徑的120倍，高度取為粒徑的520倍，以保證泥沙顆粒在沉降過程中不受壁面的干擾。模擬中采用的流體為清水，顆粒為泥沙，所有算例采用的顆粒與流體參數(shù)均相同，具體參數(shù)如表1所示。

2.2 模擬結(jié)果分析

Cheng[19]基于Brown等[20]收集的大量實(shí)驗(yàn)資料提出了計(jì)算泥沙顆粒無量綱沉速經(jīng)驗(yàn)公式

(25)

式中：w*=((ρp-ρf)/ρf·gv)-1/3，w是無量綱沉速；dp*=((ρp-ρf)g/(ρfv2))1/3，dp是無量綱粒徑。這里，將所有算例模擬結(jié)果與Cheng經(jīng)驗(yàn)公式計(jì)算值的比較結(jié)果繪制于圖2中。

由圖2可以看出，大部分模擬結(jié)果比經(jīng)驗(yàn)公式結(jié)果偏小，且隨著網(wǎng)格尺度與粒徑之比的增大，模擬結(jié)果偏小幅度增大，分析原因可能與本文選取的拖曳力模型有關(guān)，導(dǎo)致拖曳力系數(shù)選取稍大，而且隨著網(wǎng)格越來越粗，計(jì)算精度降低，導(dǎo)致結(jié)果相差越來越大。

但總體而言，模擬沉速值與經(jīng)驗(yàn)公式計(jì)算結(jié)果相差不大，對于粒徑較小的0.1 mm顆粒，比較結(jié)果隨網(wǎng)格尺度與顆粒直徑之比Δx/D增大而有所增大，但在Δx/D小于40的條件下，相差不超過3.5%。對于粒徑較大的2 mm顆粒，模擬沉速值與經(jīng)驗(yàn)公式計(jì)算結(jié)果的比較結(jié)果同樣隨Δx/D增大而增大，但是當(dāng)Δx/D≥5時(shí)，相差變化不明顯，控制在1.7%以內(nèi)，網(wǎng)格敏感性大幅降低。綜合考慮網(wǎng)格對粗細(xì)顆粒的模擬精度以及計(jì)算量的問題，同時(shí)大渦模擬要求計(jì)算網(wǎng)格不能過粗，推薦采用2～5倍泥沙粒徑模擬泥沙顆粒運(yùn)動(dòng)。

3 顆粒靜水沉降模擬

為說明采用MP-PIC方法能夠?qū)λ髂嗌诚嗷プ饔脵C(jī)理進(jìn)行分析并能夠?qū)⑵溆糜谀M和研究泥沙沉降的過程和現(xiàn)象，本節(jié)主要對不同粒徑單顆粒沉速和群體顆粒制約沉降進(jìn)行模擬研究。

圖3 模擬結(jié)果與實(shí)驗(yàn)值和經(jīng)驗(yàn)公式的比較Fig.3 Comparison among simulated results， experimental data and empirical formula

3.1 不同粒徑單顆粒沉降模擬

模擬中，選取泥沙粒徑在0.05～10 mm之間的14個(gè)算例，覆蓋了層流、紊流過渡及紊流3個(gè)沉降區(qū)，每個(gè)算例的模擬區(qū)域長寬為顆粒粒徑的100倍，高度為粒徑的500倍，以保證泥沙顆粒在沉降過程中不受壁面的干擾。初始時(shí)刻，流體流速為零，顆粒位于計(jì)算域的中軸線，并由靜止釋放自由沉降。顆粒和流體物理參數(shù)與2.1節(jié)所述相同，網(wǎng)格尺度為2倍顆粒粒徑。

將模擬結(jié)果與Brown等人實(shí)驗(yàn)值與Cheng經(jīng)驗(yàn)公式一起繪于圖3中。由圖可知，不同粒徑單顆粒泥沙沉速模擬結(jié)果與已有實(shí)驗(yàn)結(jié)果及經(jīng)驗(yàn)公式值較為吻合，證明該模型可以合理模擬較大范圍的單顆粒沉降。

將模擬結(jié)果與Cheng經(jīng)驗(yàn)公式的比較結(jié)果列于表2中。由表中可得，模擬結(jié)果與經(jīng)驗(yàn)公式的結(jié)果相差基本控制在6%以內(nèi)，模擬結(jié)果較為理想，滿足一般的模擬精度要求。

表2 模擬值與經(jīng)驗(yàn)公式計(jì)算值的比較結(jié)果Tab.2 Comparisons between simulation results and empirical formula calculations

3.2 群體顆粒沉降模擬

3.2.1 模型及參數(shù)設(shè)置

本節(jié)參考Peysson等人[21]的物模實(shí)驗(yàn)，顆粒與流體參數(shù)均與物模實(shí)驗(yàn)保持不變，模擬不同濃度泥沙顆粒的制約沉降過程，并與物模實(shí)驗(yàn)進(jìn)行對比驗(yàn)證。本模型計(jì)算域在xyz方向的坐標(biāo)范圍為[0，0.04]m×[0，0.04]m×[0，0.05]m，計(jì)算網(wǎng)格采用三維正方體結(jié)構(gòu)化網(wǎng)格，模擬區(qū)域邊界均為光滑壁面。初始時(shí)刻，泥沙顆粒按5%和10%的體積濃度隨機(jī)分布在計(jì)算域一定高度處的正方體區(qū)域內(nèi)，范圍為[0，0.04]m×[0，0.04]m×[0，0.04]m，保證顆粒沉速分布達(dá)到穩(wěn)定時(shí)與底面仍有足夠高度，顆粒由靜止自由沉降。顆粒及流體具體參數(shù)如表3所示。

表3 模型中顆粒與流體參數(shù)Tab.3 Particle and fluid parameters used for the present simulation

3.2.2 群體顆粒沉降模擬結(jié)果

按Peysson實(shí)驗(yàn)中的方法，用x=0.04n(m)(n=1,2,…,9)9組平面沿x軸將模擬區(qū)域平均分為10個(gè)體積相等的區(qū)間，待顆粒沉速達(dá)到穩(wěn)定之后，統(tǒng)計(jì)每個(gè)區(qū)間內(nèi)顆粒的平均沉速，從而得到顆粒沉速隨x軸的分布。這里將體積濃度為5%和10%兩組算例的的泥沙顆粒沉速結(jié)果與Peysson實(shí)驗(yàn)值繪制于圖4中。

4-a Φ=5%4-b Φ=10%圖4 泥沙顆粒沉速沿x軸的分布Fig.4 Distribution of settling velocity of sediment particle along x-axis

圖4中實(shí)心點(diǎn)為每個(gè)區(qū)間內(nèi)沿z軸的平均速度w‖(x)與整個(gè)模擬區(qū)域內(nèi)沿z軸的平均速度w‖的比值；空心點(diǎn)為每個(gè)區(qū)間內(nèi)垂直于z軸的平均速度w⊥(x)與整個(gè)模擬區(qū)域內(nèi)沿z軸的平均速度w‖的比值。由圖可知，模擬中間區(qū)域顆粒沉速較大，靠近邊界壁面沉速較小，與群體顆粒沉降存在內(nèi)部對流的物理現(xiàn)象較為符合。而且顆粒主要沿z軸方向運(yùn)動(dòng)，垂直于z軸方向速度較小。整體沉降速度分布趨勢與Peysson物模實(shí)驗(yàn)大致相同。

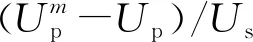
由于沉降時(shí)顆粒之間會(huì)產(chǎn)生碰撞和干擾，群體顆粒沉降速度小于單顆粒沉速，并且隨著顆粒濃度的增加，群體顆粒沉速越來越小。Richarson和Zaki[22]利用量綱分析法得到了群體沉速的計(jì)算公式為

wg/w0=(1-Φ)m

(26)

式中：wg與w0分別為群體顆粒及單顆粒的沉速；Φ為泥沙顆粒的體積濃度；m為冪指數(shù)，本文與Peysson相同取為5。將5%和10%的模擬結(jié)果與理論公式，實(shí)驗(yàn)值繪制于圖6，發(fā)現(xiàn)MP-PIC方法模擬結(jié)果與Peysson實(shí)驗(yàn)值有一定偏離，但偏離均在實(shí)驗(yàn)結(jié)果的誤差線內(nèi)。模擬結(jié)果與理論公式的誤差隨體積濃度的增大而減小，當(dāng)體積濃度Φ=5%時(shí)，二者相差3.49%，當(dāng)體積濃度Φ=10%時(shí)，相差僅為0.17%。同時(shí)，模擬結(jié)果的顆粒沉速同理論公式一樣具有隨體積濃度增大而減小的趨勢，能夠較好地模擬群體顆粒沉降。

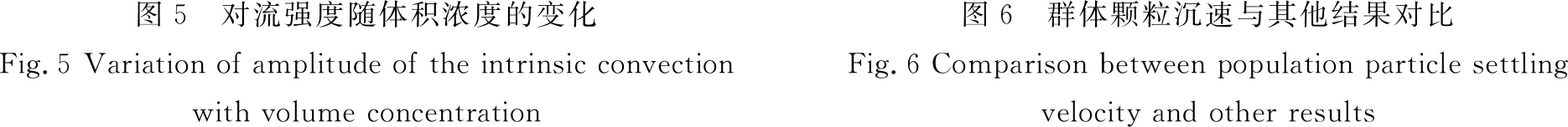
圖5 對流強(qiáng)度隨體積濃度的變化Fig.5 Variation of amplitude of the intrinsic convection with volume concentration圖6 群體顆粒沉速與其他結(jié)果對比Fig.6 Comparison between population particle settling velocity and other results

4 結(jié)論

本文基于MP-PIC方法，采用歐拉方法描述液相，用拉格朗日方法描述顆粒相運(yùn)動(dòng)，建立了描述泥沙靜水沉降運(yùn)動(dòng)的數(shù)值模型，分別對網(wǎng)格敏感性、單顆粒沉速和群體顆粒制約沉降等問題進(jìn)行研究，可以得出：

(1)該模型具有對水流泥沙相互作用機(jī)理進(jìn)行分析的能力，能夠用于模擬和研究泥沙沉降的過程和現(xiàn)象。

(2)通過模擬單個(gè)泥沙顆粒在靜止水體中自由沉降，討論模型對計(jì)算單元網(wǎng)格的敏感性問題。為盡量縮小模擬結(jié)果與經(jīng)驗(yàn)公式結(jié)果之間的差距，但是又不能使得計(jì)算量太大，同時(shí)考慮到大渦模擬對計(jì)算網(wǎng)格不能過粗的一般要求，推薦采用2～5倍泥沙粒徑的網(wǎng)格尺度來模擬泥沙顆粒運(yùn)動(dòng)。

(3)將不同粒徑單顆粒泥沙沉速與Brown等人實(shí)驗(yàn)值、Cheng經(jīng)驗(yàn)公式進(jìn)行對比，結(jié)果較為吻合，證明MP-PIC模型可以較好模擬不同粒徑單顆粒泥沙運(yùn)動(dòng)。

(4)模擬了不同體積濃度泥沙顆粒的制約沉降過程，結(jié)果顯示，模擬中間區(qū)域顆粒沉速較大，靠近邊界處沉速較小，并且垂直于沉降方向的速度接近為零，與Peysson物模實(shí)驗(yàn)較吻合，充分體現(xiàn)了群體顆粒的沉降對流現(xiàn)象；同時(shí)，群體顆粒沉速模擬結(jié)果與理論公式相差不大，具有隨體積濃度增大而減小的趨勢，采用MP-PIC方法能夠很好地對泥沙顆粒靜水沉降進(jìn)行三維數(shù)值模擬研究。