一種基于虛擬導航點的超低空飛行器威脅回避算法研究

尹明新，姜 偉,孫 騫

(1.四川航天系統工程研究所, 成都 610100；2.零八一電子集團科技公司, 成都 611731;3.哈爾濱工程大學, 哈爾濱 150001)

0 引言

超低空飛行技術是提高亞聲速無人飛行器生存和突防能力的重要手段。該技術可有效利用地形和地雜波的掩護，大幅降低飛行器被探測到的概率，增大敵方防御系統的攔截難度。其中，地形跟蹤、地形/威脅回避技術的發展是超低空飛行的關鍵[1]。

目前,具有地形/威脅回避功能的飛行器，主要是通過事先規劃好的飛行走廊實現地形回避的。但在實際飛行過程中，常常會發生一些突發的狀況，出現先前未探測到的威脅，如探測雷達、敵方攔截飛機的來襲等。另外，在工程應用中也遇到了一個很大的問題，就是障礙物圖的保障，飛行走廊內一些細小的障礙物信息(如高壓線、桿塔、線塔等)，無法通過數字高程圖和現有的障礙物保障圖來獲取。這些情況的出現，使得預先設定的航跡很有可能會穿越未知威脅的作用區域，造成飛行器的風險系數驟然增大。因此，生存和突防要求迫使超低空飛行器必須具備自主威脅回避的能力。

常用的地形/威脅回避算法有梯度法[2]、啟發式搜索算法(A*算法)[3]、動態規劃法[4]、遺傳算法[5]等，但這些常用于離線的地形/威脅回避航跡規劃[6]，普遍存在計算量大、易陷入局部最優等問題。針對突發威脅的情況，現階段仍沒有一個比較成熟且可直接工程應用的自主威脅回避算法。

近年來，基于被動雷達無源定位的自主探測技術使得飛行器逐漸具備了威脅感知的能力[7]，同時國內外利用前視序列圖像實現障礙物檢測和距離解算的技術研究已經取得了一定成果[8]。本文以自主探測為基礎，結合超低空無人飛行器的飛行特點，提出了一種基于虛擬導航點的威脅回避算法。該算法設計簡單，計算量小，易于實現，能夠有效保證飛行器在超低空飛行走廊中的安全。

1 問題描述

超低空飛行走廊是立足于預先或者當前已經掌握的所有戰場環境信息，采用全局最優規劃方法離線獲得的。在現代戰爭中，由于戰場態勢瞬息萬變，矛與盾之間的對抗程度越來越強，加上超低空無人飛行器多為亞聲速巡航，在長時間的飛行過程中威脅環境和預定任務的形態都極有可能發生變化，飛行器的突防難度變得越來越大。另外，在預定規劃的超低空飛行走廊內，還可能存在通信信號塔、高壓線塔、高壓線等障礙物[9]，這些障礙物的高度有些可達百米級，并且在航跡規劃時該類障礙物的信息很難全面獲取，這給飛行器超低空飛行的安全帶來了極大威脅。在這些情況下，離線規劃出的最優航跡已不能滿足任務需求。因此，對飛行器面對突發威脅時的自主回避問題的研究是十分迫切且具有重要意義的。

隨著現代信息技術和傳感器技術的不斷發展，基于視覺、雷達的感知手段層出不窮，在線數據獲取、傳遞以及自主探測技術使飛行器逐漸具備了強大的環境感知能力。同時，計算機快速處理技術和海量存儲技術的快速發展使得無人飛行器具備了自主智能飛行的可能[10]。

面對突發威脅時能夠進行自主回避是亞聲速超低空無人飛行器自主飛行的重要特點。本文研究的無人飛行器利用射頻傳感器及紅外探測器進行自主飛行，具有探測未知威脅和障礙的能力，可在飛行過程中及時發現處于航線上的威脅，并甄別威脅類型。其中射頻傳感器可識別防空雷達等威脅的位置和作用距離，紅外探測器可識別電線塔、煙囪等障礙物的距離及大小。本文以此為前提，針對預定飛行走廊內的某一范圍區域環境發生改變(如發現預定航跡上存在探測雷達、防空火力網、障礙物等威脅)問題研究威脅回避策略。飛行器可以在線改變飛行航跡，對這些區域進行自主回避。

2 基于虛擬導航點的威脅回避原理

無人飛行器自主飛行主要依靠慣性/衛星組合以及其他輔助導航手段，在各導航點之間大都按照直線飛行。下面首先介紹了在直飛航跡上出現突發威脅時基于虛擬導航點的威脅回避原理，定義為方案A(見圖1)。

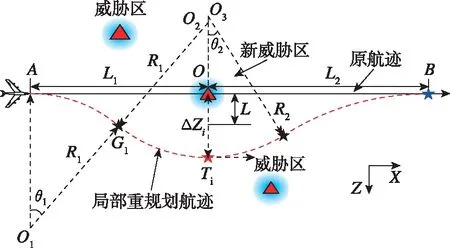
圖1 直飛過程威脅回避(方案A)Fig.1 Threat avoidance on straight-flight process (Strategy A)

按照上述原理生成的航跡仍有可能會穿過其他已經探測到，但并不在原航跡上的威脅。因此，本文設計了多條回避航跡，利用不同的偏航距離ΔZi生成不同的虛擬導航點，即N個ΔZi對應N條航跡。最后，再設計回避代價函數(其主要與航程代價、威脅代價以及高度代價相關)，N條航跡即對應N個代價函數值，其中對于經過其他威脅的航跡，其代價可以設為無窮大。這樣即可在生成的N條航跡中，選擇代價最小的一條航跡作為回避航跡。

因為飛行器對威脅的探測距離有限，因此不可能完全發現新航跡A—Ti—B上的未知威脅，尤其在回歸航跡TiB及其后面的航跡段。當飛行器按照方案A機動回避時，有可能在轉彎飛行過程中發現前方航跡上又出現了新的威脅，該問題本質上可以歸結為如何從與回歸航向不平行的當前航向又重新回歸到原航跡的問題，本文根據當前航向角與回歸航向角的大小分兩種方案解決。

方案B：在規避航跡C—Ti—B上發現前方航跡存在威脅，即當前航向角小于回歸航向角，如圖2所示。

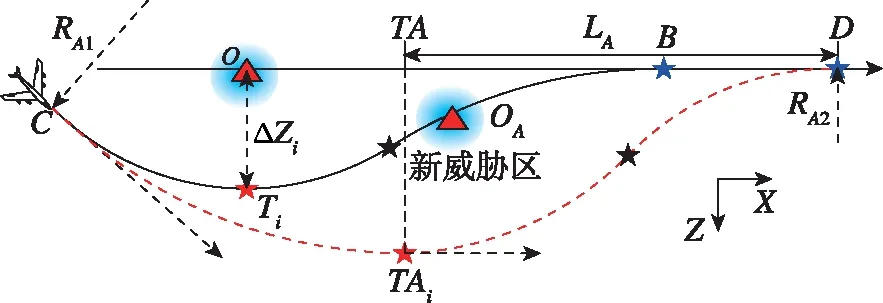
圖2 機動過程威脅回避(方案B)Fig.2 Threat avoidance on maneuvering process (Strategy B)

假設飛行器在C點探測到前方航跡TiB上存在新的威脅區域，則可以RAi為轉彎半徑進行側向機動，直至到達另一個虛擬導航點TAi，此時瞬時航向與回歸航向平行，問題又變成了在與原航跡平行的航跡上如何回歸的問題，可以按照方案A中回歸航跡的計算方法計算出回歸航跡TAiD，此時不同的轉彎半徑RAi將得到不同的虛擬導航點TAi。因此，同樣可以通過控制不同的轉彎半徑RAi在線規劃出N條航跡，然后按照回避航跡評價方法選擇一條代價最小的航跡即可。

方案C：在回歸航跡TiB上發現前方航跡存在威脅，即當前航向角大于回歸航向角，如圖3所示。

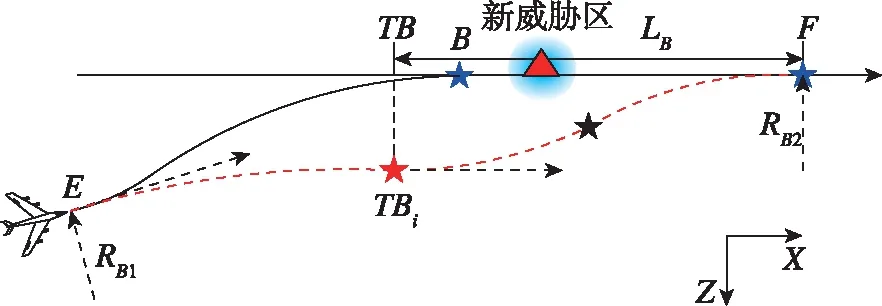
圖3 機動過程威脅回避(方案C)Fig.3 Threat avoidance on maneuvering process (Strategy C)

假設飛行器在E點探測到前方航跡存在新威脅區，則可以RBi為轉彎半徑進行機動，到達虛擬導航點TBi，該虛擬導航點可位于原航跡的任意一側(取決于RBi的大小和機動方向)，此時瞬時航向與回歸航向平行，最后再規劃出回歸航跡TBiF重新回到原航跡。

通過分析可以發現，當飛行器即將貼近原始航跡，即瞬時航向快逼近原航向時，如圖4所示，如在G點發現前方直線航跡上又出現新的威脅區，如果仍按照上述方法進行規避，則可能由于航向偏轉角的限制，生成的虛擬導航點會很靠近原航跡，偏航距離將非常有限，導致回歸航跡將不能使飛行器成功回避威脅。對于這種情況，可以利用探測器的探測范圍遠比威脅半徑大的特點，待飛行器重新回到原始航跡上的B點后，再按照相應的策略重新進行威脅回避。

圖4 機動轉直飛過程威脅回避Fig.4 Threat avoidance on maneuvering to straight-flight process

本文的方案B和方案C，其本質都是研究如何從與回歸航向不平行的當前航跡重新回到原航跡的問題，解決思路都是讓飛行器先通過轉彎進行側向機動，直至使當前航向與原航跡所在的回歸航向保持平行，然后再按照對應算法生成回歸航跡，得到完整的回避航跡。這種思路同樣適用于在非直線航跡上規避威脅的問題，解決方法是一致的。

3 算法設計

3.1 基本假設

本文的算法以飛行器具備自主探測威脅的能力為基礎，滿足以下基本假設條件：

1)射頻傳感器具備全方位探測能力，能夠根據先驗信息甄別威脅種類、位置及作用半徑。

2)紅外探測器可實現障礙物檢測，可識別障礙物的距離和大小；受水平視場角(半視場角為α)的限制，探測范圍有限；視場中心線水平投影與速度矢量水平投影重合。

3.2 幾何解算

利用本文提出的方法自主回避威脅的關鍵是計算虛擬導航點的位置、飛行器機動轉彎半徑，同時確定航向偏轉角。設飛行器原航跡的航向角為ψ，威脅中心在航跡上的投影為O′，與A點的距離L1≈Rc(可以等效為射頻或紅外探測距離)，設飛行器發現威脅區時的位置為(xs，ys)，則O′點的位置為：

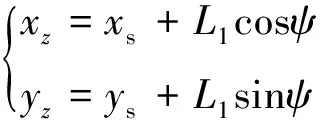
(1)

求解虛擬導航點Ti的位置：

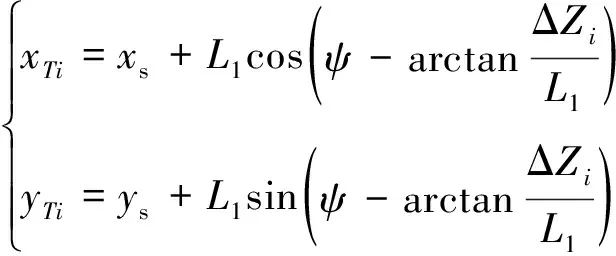
(2)

其中，ΔZi為虛擬導航點Ti到原航跡的距離，即偏航距離。考慮到飛行器機動能力限制的因素，本文將AG1段和G1Ti段的轉彎半徑設計為同一個值R1，由幾何關系可以計算機動轉彎的2個重要參數：

(3)

其中，θ1為從A點到G1點以及從G1點到Ti點的航向偏轉角(即轉彎過程對應的圓心角)，回歸航跡TiB的相關參數同理可求。

式(3)表明，當偏航距離ΔZi一定時，探測距離L1越大，轉彎半徑R1越大，這是有利于飛行器機動的，即越早發現威脅，則越能以最小的代價避開威脅。當探測距離L1一定時，如果ΔZiL1，那么ΔZi越大，轉彎半徑越大。一般來說，射頻和紅外傳感器的探測距離L1均遠大于其能探測到的威脅源的半徑，因此偏航距離ΔZi不可能大于探測距離L1，所以ΔZi越大，轉彎半徑越小，對飛行器的機動要求越高，且回避航跡的航程越長，規避威脅的代價越大。

在利用紅外探測器進行障礙物回避時，還涉及由最小轉彎半徑和視場角限制引起的最大航偏距的問題。設飛行器的最小轉彎半徑為Rmin，則可以根據整條回避航跡求出最大的偏航距離為：

ΔZmax=min(ΔZmax1，ΔZmax2)

(4)

其中，轉彎半徑越小，偏航距離越大，則由最小轉彎半徑Rmin，可根據式(3)解算出ΔZmax1；回避航跡上可能出現其他威脅，因此回避航跡應該始終處于飛行器的探測范圍內，則由半視場角α，根據圖5幾何關系，可以解算出由半視場角確定的最大偏航距離ΔZmax2。

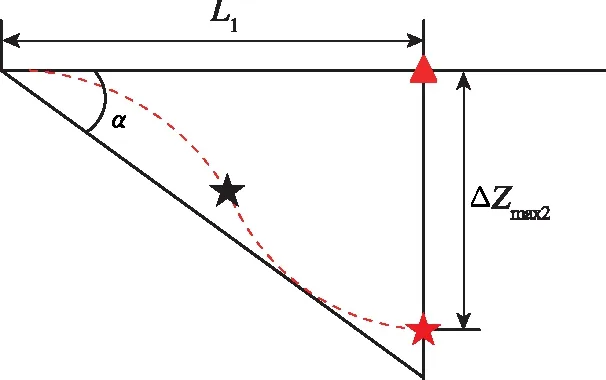
圖5 視場角與航偏距之間的關系Fig.5 Relationship between FoV-angle and offtrack-range

根據幾何關系，可解算出：

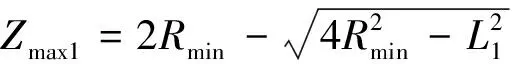
(5)

對于當前航向與回歸航向不一致的情況，以圖2為例，設在規避航跡的C點(xf，yf)發現目標時，飛行器的當前轉彎半徑為Rf，航向角為ψf，此時根據不同的轉彎半徑Rfi可以得到虛擬導航點TAi的位置為：

(6)

一旦求解出虛擬導航點TAi的位置后，即可按照相應的算法生成對應的回歸航跡。

3.3 回避代價函數

本文設計的威脅回避算法需要根據不同的偏航距離或轉彎半徑實時解算出N條待選回避航跡，建立對應的代價函數，并從中選擇代價最小的航跡，從而有效地規避威脅區域。為了表征回避航跡的綜合性能，對各個影響因素按照歸一化原則轉化為0～1之間的數值，然后再確定各個單項指標在綜合指標中的權重，最后得到一個表征回避航跡綜合指標的數值。

回避代價主要與偏離原航跡的距離、威脅程度、高度代價(保證地形跟蹤性能)相關，據此建立代價函數：

f(l)=w1z(l)+w2t(l)+w3h(l)

(7)

其中，z(l)為虛擬導航點到原航跡的距離，表征航程代價；t(l)為重規劃航跡的威脅代價，如果航跡上有新的威脅或障礙，則可取為無窮大；h(l)為高度代價，其表達式為：

h(l)=var(l)+dh(l)+mane(l)

(8)

表征地形跟蹤的性能，與離地高方差、平均離地高及縱向機動代價有關。本文根據預測的側向航跡以及地圖高程信息，利用飛行器縱向控制回路特點在線預測對應N條側向航跡的N條縱向航跡，計算高度代價。w1、w2、w3分別為相應代價的權重。

發現威脅后，在三維空間中預測N條三維航跡。這樣即可在N條航跡中，選擇出代價最小的航跡作為回避航跡。

3.4 算法流程

根據前面的介紹和分析，圖6給出了基于虛擬導航點的超低空威脅回避算法流程。當飛行器在飛行過程中利用自主探測設備發現前方航跡穿過威脅區域后，可根據自身的飛行狀態，選擇相應的回避策略。

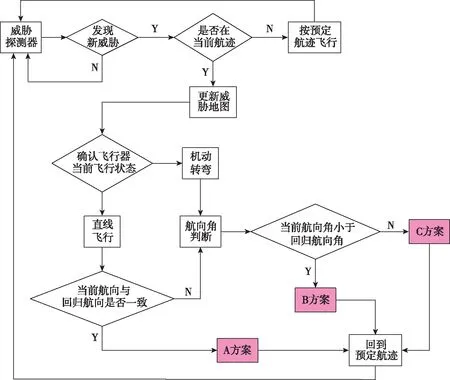
圖6 算法流程圖Fig.6 Algorithm flow diagram

4 仿真算例

4.1 仿真條件

利用Matlab軟件對超低空飛行器威脅回避算法進行仿真。考慮到射頻傳感器的探測距離較遠，回避過程相對簡單，本文主要針對紅外探測器發現威脅源(障礙物)時的回避算法進行驗證。采用隨機生成的大小為15km×15km的三維數字地圖進行仿真，地圖分辨率25m×25m，如圖7所示。

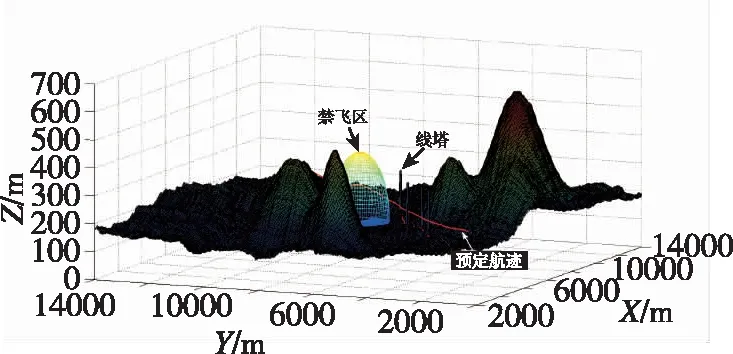
圖7 三維數字地圖Fig.7 3D digital map

設紅外探測器的探測距離Rc=6km，半視場角α=4°；飛行器最小轉彎半徑Rmin=10km，縱向質心控制回路時間常數τ=7s，安全離地高度h0=50m；地形跟蹤最大和最小離地高度分別為100m和20m；代價權重w1=0.2、w2=0.4、w3=0.4；障礙物為1m×2m×150m的線塔，離障礙物的安全距離取40m，仿真中在預定航跡上及飛行走廊內設置有4組大小一致的線塔。

4.2 仿真結果及分析

當飛行器在飛行過程中發現原航跡上出現了新的威脅后，利用基于虛擬導航點的威脅回避算法可快速生成回避航跡，并沿著新的航跡進行機動轉彎飛行，成功實現對威脅的規避，同時能夠準確回到初始航線上，仿真結果如圖8和圖9所示。

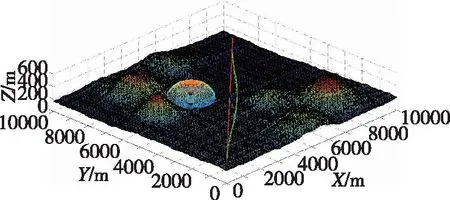
圖8 直飛過程威脅回避三維航跡Fig.8 3D trajectory of threat avoidance on straight-flight process

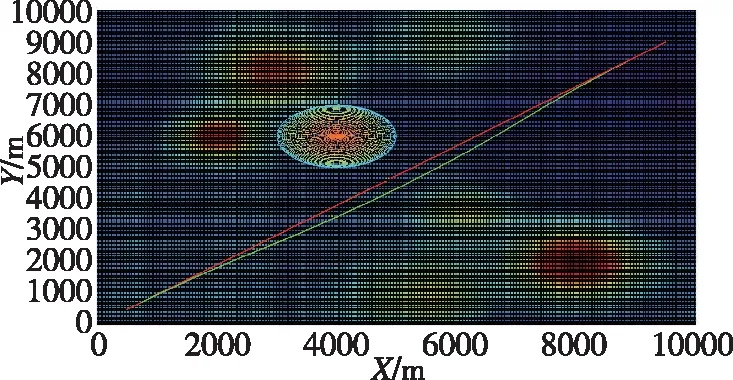
圖9 直飛過程威脅回避二維航跡Fig.9 2D trajectory of threat avoidance on straight-flight process

當飛行器在機動規避的過程中再次探測到前方回歸航跡上存在新的威脅(此時當前飛行航向與回歸航向不一致)，采用相應的算法快速計算出可行的虛擬導航點，生成另一條重規劃航跡，實現了在機動規避過程中的威脅回避，同時回歸到預定設計的航跡上，仿真結果如圖10和圖11所示。

圖12所示為利用飛行器的縱向機動能力預測的縱向飛行航跡，用于回避代價的計算。

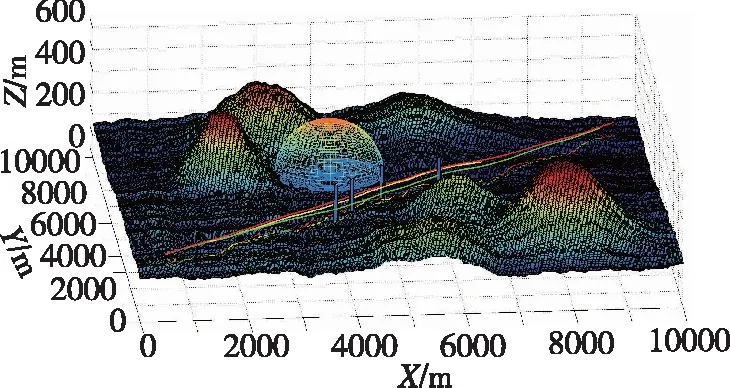
圖10 機動過程重新發現威脅后的三維回避航跡Fig.10 3D trajectory of threat avoidance on maneuvering process

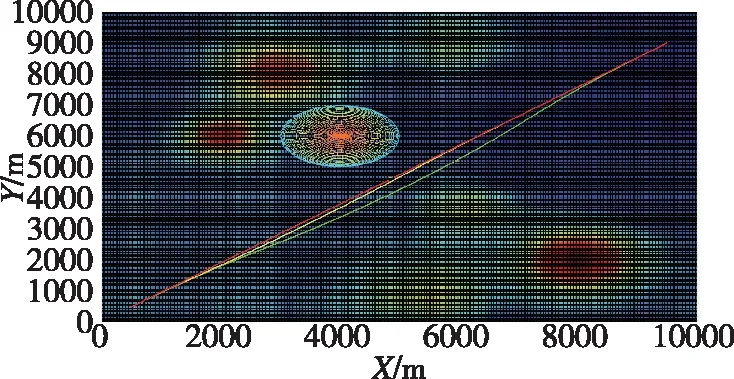
圖11 機動過程重新發現威脅后的二維回避航跡Fig.11 2D trajectory of threat avoidance on maneuvering process

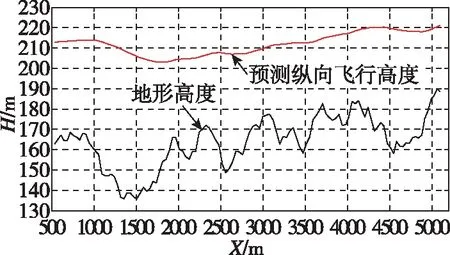
圖12 縱向預測航跡仿真結果Fig.12 Simulation result of vertical predict trajectory

以上仿真結果表明，該算法計算量小，計算速度快，對計算機內存和處理速度的要求不高，能夠適用于亞聲速無人飛行器在線進行威脅回避的使用需求。

5 結論

對突發威脅或障礙快速做出反應是飛行器實現智能自主飛行的關鍵[11]。本文從飛行器在突發威脅下進行自主回避的實際需求出發，采用基于虛擬導航點的威脅回避算法，對飛行器自主威脅回避問題進行了初步研究，取得了比較滿意的結果。

該算法具有普遍的適用性，還可以用于基于視覺的飛行器智能避障或局部在線航跡重規劃等技術研究中。本文提出的算法原理簡單，相比于全局尋優算法計算量小，易于工程實現，對于實現飛行器自主、智能化具有重要意義。由于該算法是以犧牲全局最優為代價來獲取快速計算結果的，因此后續還需要針對不同類型的仿真環境進一步驗證算法的適應性和有效性。