基于滑模變結構和擴張狀態觀測器的電動舵機復合控制方法

吳 真，曹東海，熊官送

(北京自動化控制設備研究所，北京 100074)

0 引言

舵機是飛行器控制系統的重要組成部分，是控制系統中特性復雜、能耗高、配套數量多、工作環境惡劣的子系統，其性能和可靠性對姿態控制具有決定性的影響，直接決定了飛行器飛行結果的成敗和精度。在實際飛行過程中，舵偏角的變化和環境中風阻等因素的影響導致舵機承受的鉸鏈力矩變化。文獻[1]采用了自抗擾控制技術應用到電動舵系統中，基本思想是采用PD控制與擴張狀態觀測器相結合，取得了理想的控制效果。

在解決復雜的非線性系統問題時，滑模變結構作為一種綜合方法得到了重視，具有很強的魯棒性，其對系統參數攝動的不敏感是以控制量的高頻抖動來換取的。系統要求電動舵機能在有限時間內跟蹤指令，對于理想的被控對象，通常滑模控制[2]是通過選取合理的滑模面參數來保證狀態空間任意位置運動點在有限時間內到達滑模面。針對高精度的伺服系統，實際存在很多的不確定項，且無法準確得知不確定項的上界。許多學者們提出了不同的方法對不確定干擾進行估計和辨識[3-5]，算法涉及較多參數，調參復雜，實用性不強。文獻[6]提出了使用擴張觀測器估計電機負載轉矩，使電機具有了更好的性能；文獻[7]采用邊界層與低通濾波器技術的滑模控制算法，同時對摩擦進行建模，在小角度時獲得良好的跟蹤效果，但對系統中的擾動只是假定上界，未能實時估計擾動。

本文針對電動舵機高精度伺服的特點，采用了擴張狀態觀測器對電動舵機運行中的負載擾動進行實時觀測，提出了將線性擴張狀態觀測器與滑模變結構控制相結合，并給出了設計過程，最后通過仿真和實驗對算法的合理性加以驗證。

1 電動舵機的數學模型

電動舵機是控制飛行器舵面偏轉的伺服系統，其主要由舵機控制器、功率驅動、伺服電機、傳動結構和反饋傳感器五部分組成，輸入為舵控指令信號，結構組成如圖1所示。

圖1 電動舵系統結構框圖Fig.1 Structure diagram of electromechanical actuator system

電動舵機控制器接收制導機給定的控制指令和傳感器的反饋信號，計算出脈沖寬度調制(Pulse Width Modulation，PWM)控制信號。由驅動器驅動伺服電機，通過電機驅動減速傳動機構帶動舵面的偏轉，舵面偏轉角度經反饋電位計反饋至控制器形成閉環控制。

本文所涉及電動舵機經簡化所得數學模型如圖2所示。

圖2 電動舵系統數學模型Fig.2 Mathematical model of electromechanical actuator system

其中：L為電機繞組電感；R為電機繞組電阻；Kt為電機力矩系數；J為舵機折算到電機軸的總轉動慣量；Ki為電機到輸出軸的傳動比；Ke為電機反電動勢系數；B為電機阻尼系數；TL為外加負載。

首先考慮被控對象，在開環條件下，由結構框圖可以得到控制器輸出到舵偏角的傳遞函數為：

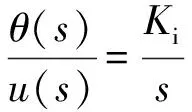
(1)

電機模型中電氣時間常數τe=L/R，機電時間常數τm=JR/(KtKe)，由于其電氣時間常數和電機阻尼較小，為方便研究，可以忽略，被控對象可以簡化為：

(2)

將簡化后的傳遞函數轉化為微分方程形式，即為：

(3)

此微分方程表示了舵偏角與控制電壓之間的關系，通過調節電壓實現對舵機的控制。

2 滑模變結構控制器

滑模變結構控制[8]是一種非線性控制策略，它的控制特性迫使系統在進入滑動模態時沿著規定的狀態軌跡作小幅度、高頻率的運動，與系統的參數及擾動無關，滑模面是可設計的。針對如下被控對象：

(4)

滑模面設計為：

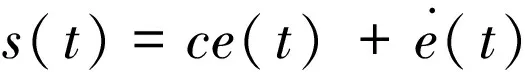
(5)

其中，c>0且滿足Hurwitz條件,e(t)=θd-θ,θd為期望指令信號。

由于滑模變結構控制存在高頻抖動，為了抑制抖動，本文采用指數趨近律的方法。

指數趨近律表達式為：

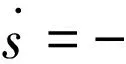
(6)

(7)

由式(3)～式(6)可得，舵機的滑模控制律為：

(8)

由于舵機實際運行中存在鉸鏈力矩、伺服電機本身及傳動機構間隙等非線性因素，且滑模函數的未知干擾d無法準確獲得上界。為了對未知干擾實時估計并進行補償，本文提出了采用擴張觀測器的方法對不確定項進行補償，把摩擦、負載等不確定因素等效為干擾進行補償。

3 擴張狀態觀測器

擴張狀態觀測器(Extended State Observer，ESO)[9]是自抗擾控制器(Active Disturbance Reje-ction Control，ADRC)的核心部分，能對動態和不確定性的擾動進行綜合估計。由于非線性擴展觀測器參數較多，調節復雜，在實際應用中不能通過參數調節快速控制目標，所以本文采用線性擴張狀態觀測器對舵機不確定項進行估計[10]。

針對二階被控對象式(3),考慮未知干擾d，轉換為狀態方程形式如下：

(9)

(10)

4 擴張狀態觀測器與滑模變結構復合的舵系統控制設計

本文涉及的電動舵機僅有電位計的反饋信號，采用位置閉環，其控制結果框圖如圖3所示。

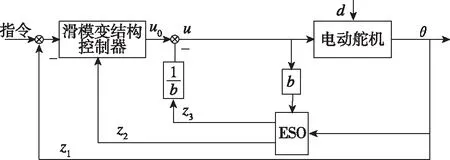
圖3 基于擴張狀態觀測器的滑模控制結構圖Fig.3 Structure diagram of the sliding model control based on ESO

其中，ESO為三階擴張狀態觀測器，輸出的z2速度觀測值作用到滑模變結構控制器，z3是由擴張狀態觀測器估計的總擾動量，補償到控制器輸出。

在實際舵系統的跟蹤系統中，指令信號的頻率比較低，采樣頻率達到了2kHz,所以指令信號的速度和加速度可以簡化為零，由此可以得到電動舵機的實際控制器輸出為：

(11)

5 仿真驗證

實驗樣機的電動舵機參數如表1所示,滑模變結構控制器與擴張狀態觀測器各參數如表2所示。

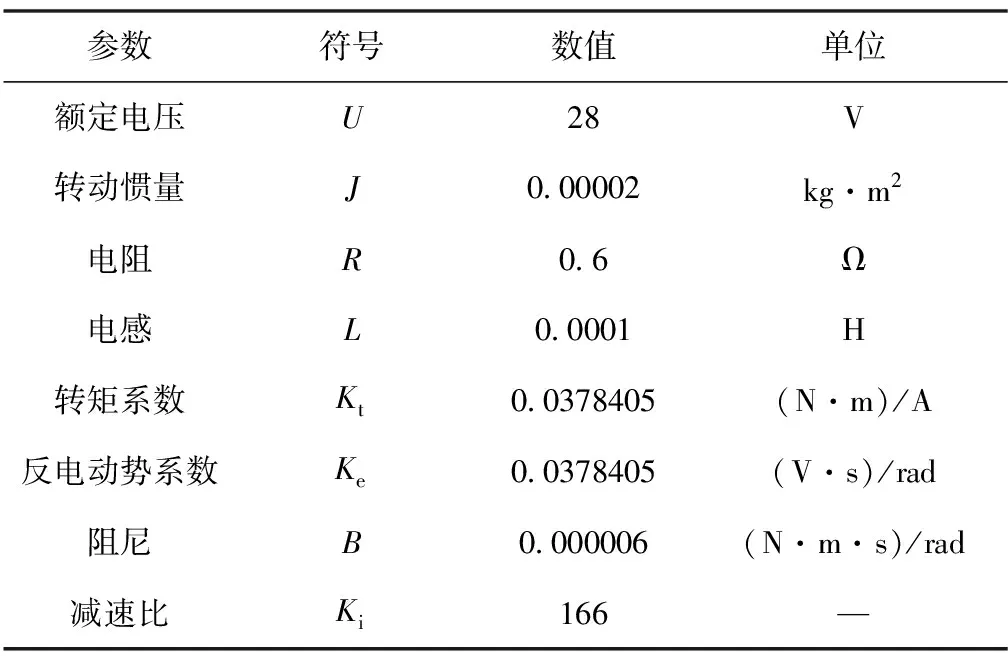
表1 電動舵機參數

表2 控制器各參數表

為了比較本文所提出的擴張狀態觀測器進行補償的滑模變結構控制器與常規滑模變結構控制器的性能，對其進行仿真驗證。

在Matlab/Simulink環境下，建立舵系統仿真模型。給定5V(10°)階躍指令，施加4(N·m)/(°)的彈性負載，得到的仿真結果如圖4所示。

仿真結果表明，給定大角度階躍信號時，常規滑模變結構控制存在一定的靜差，由于擴張觀測器的存在，對負載進行觀測，補償到控制器中，可以有效減小靜差，提高控制精度。

6 實驗結果

為了驗證仿真結果，在滑模控制器的參數保持不變的前提下進行樣機實驗。在4(N·m)/(°)彈性負載條件下，通過施加不同舵控指令來研究其控制算法的效果。圖5所示為給定輸入信號1V階躍，得到兩種算法的位置跟蹤曲線。圖6所示為給定輸入5V階躍的響應曲線。

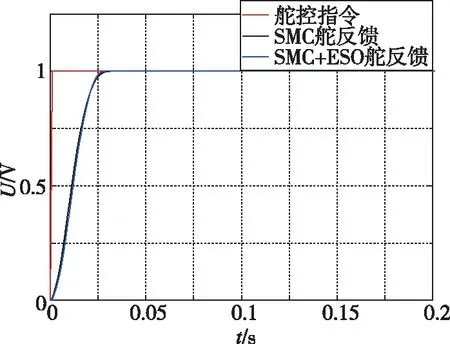
圖5 1V帶載階躍響應曲線Fig.5 1V step response with load

圖6 5V帶載階躍響應曲線Fig.6 5V step response with load

從表3實驗結果對比可知，系統到達目標位置后未出現超調現象，帶擴張觀測器的控制算法在小角度帶載情況下與常規滑模控制算法作用效果差不多。常規滑模控制算法自身的抗干擾能力足以克服小角度時的負載擾動量，在大角度時，實驗效果和仿真實驗同樣出現了一定的靜差，而擴張觀測器的作用則是縮小靜差。

表3 實驗結果對比

圖7所示為小角度時1V，1Hz條件下施加4(N·m)/(°)彈性負載所得實際電動舵機正弦跟蹤曲線。從圖7中可以看出，本文提出的控制器能在速度過零時，跟蹤誤差明顯減小。圖8所示為實時觀測器的補償控制量，在過零點處補償量最大，折算到控制信號占空比為5.5%。表明了本文提出的方法有效可行，使得電動舵機伺服控制得到進一步提高。

為驗證大角度正弦位置跟蹤效果，在彈性負載4(N·m)/(°)條件下，給定5V3Hz的舵控指令，實驗跟蹤效果曲線如圖9所示，大角度時，在速度過零點處依然能夠準確跟蹤指令信號。觀測器估計的干擾補償量如圖10所示。過零處補償量折算到控制信號占空比達到17.5%。

圖7 1V 1Hz位置跟蹤曲線Fig.7 1V 1Hz position tracking

圖8 1V 1Hz干擾補償曲線Fig.8 1V 1Hz compensation cure of disturbance

圖9 5V 3Hz位置跟蹤曲線Fig.9 5V 3Hz position tracking

7 結論

本文設計了滑模變結構與擴張觀測器相結合的控制策略，通過擴張觀測器觀測電動舵機不確定模型因素和外加干擾，用于補償其對系統的影響，在Simulink中驗證算法的有效性。最終，通過某型電動舵機實物驗證了算法的正確性和有效性。特別是針對在大負載情況下，補償效果尤其明顯，取得了很好的控制效果，具有很好的工程應用價值。