戰術導彈氣動伺服彈性滑模控制技術

張公平，段朝陽，趙艷輝，鄭鹍鵬

(1.中國空空導彈研究院，洛陽 471099；2.航空制導武器航空科技重點實驗室，洛陽 471099)

0 引言

自可控飛行器誕生以來，氣動伺服彈性(Aeroservoelasticity，ASE)就一直是飛行控制系統設計必然面對的難題之一。針對不同用途的戰術導彈，國內外相關研究機構設計了形式各異的ASE控制算法，其原理多采用被動式濾波。根據中心頻率設計陷波器，從一定程度上緩解了ASE的不良影響，但同時也帶來了系統的魯棒自適應問題，即引入結構濾波器的閉環系統在彈體彈性模態時變特性難以精確建模的現實條件下，經常出現飛行狀態振蕩、執行機構飽和，甚至操縱失穩等現象[1-4]。

近年來，為適應空天一體作戰、突破敵防御系統、快速精確打擊等任務需求，普遍要求導彈結構輕量化，以使其具備高速、高過載與遠射程能力。然而，在高速飛行時，輕量結構在外界激勵下，更易發生彈性振動，并導致控制異常。以美國某空空導彈項目為例，其前期試飛遭遇了嚴重的ASE問題。分析認為，彈體彈性振動信號進入飛行控制系統后，被舵機高頻響應，氣源消耗殆盡，導致舵不跟隨，從而引發彈體失控翻滾[5]。因此，需要引入結構濾波器，并使其參數隨彈體結構特性變化。為準確獲取實際飛行過程中的彈體結構特性，常采用在線辨識技術[6-8]。

隨著傳感器帶寬及舵機性能的進一步提高，彈體彈性振動更容易被敏感并被響應，導彈ASE問題更加凸顯。本文通過建立某戰術導彈高精度耦合彈性動力學模型，針對其時變特性，設計了自適應結構濾波器。然后，在經典三回路控制架構下，采用極點配置方法自動優化增益，并對主增益設計局部切換面進行二次調節，從而實現彈性彈體的滑模變結構控制，改善系統魯棒性。最后，通過聯立剛體動力學模型，對導彈ASE控制技術進行非線性仿真驗證。

1 導彈氣動伺服彈性動態建模

1.1 彈性基準坐標系定義

為描述彈體結構彈性變形程度，定義彈性基準坐標系如圖1所示。

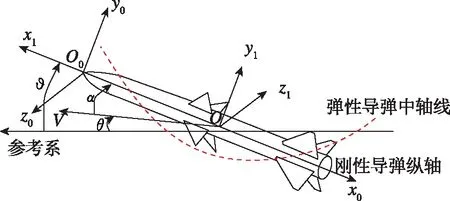
圖1 彈性基準坐標系示意圖Fig.1 Schematic of elasticity reference coordinate frame

圖1中，O0X0Y0Z0即為彈性基準系，其三軸分別與彈體系OX1Y1Z1三軸平行。

1.2 高精度耦合動態建模

長細比較大的戰術導彈在法向力作用下，振動方程如下：

(1)

其中，EJ(x)為彈性基準系某截面x處的抗彎剛度，m(x)為線密度，Wy(x,t)為法向力。則基于模態疊加與變量分離原理[9]，可設彈性變形量為：

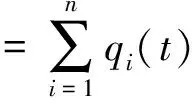
(2)

式中，φi(x)為第i階振型，qi(t)為對應的廣義坐標。

在兩端自由梁假設及零初始條件下，將式(2)代入式(1)，整理可得廣義坐標方程：

(3)

式中，ξi為結構阻尼比，ωi為固有振動頻率，Qi為廣義力，廣義質量為：

(4)

若考慮氣動力、舵控力與舵慣性作用，則廣義坐標方程右端項寫成廣義加速度的形式為：

(5)

其中，各系數定義如下：

(6)

式中，α與ωz所在項代表了剛體轉動與彈性振動的耦合影響。

1.3 線性動態建模

考慮到現有技術對分布式氣動特性的預測精度與非線性仿真可信度的需求，對式(5)作簡化處理，并進行Laplace變換，可得由彈性振動引起的俯仰角速率及加速度對舵偏的傳遞函數為：

(7)

其中，xg與xa分別為速率陀螺與加速度計的安裝位置，Ci與Di分別為舵控力與舵慣性的影響。根據試飛數據的辨識結果可知，結構振動與飛控系統的耦合特性主要受集中力影響[9]。

2 模態自適應結構濾波器設計

在實踐中，結構濾波器設計與系統穩定裕度校核之間的關系如圖2所示。

圖2 彈性穩定裕度校核流程示意圖Fig.2 Flow diagram of stability margin verification

針對彈性彈體的增益穩定，常采用凹陷結構濾波器[10]，利用其高頻零點與彈性彈體的高頻極點對消，形式如下：

(8)

其中，ωp越小濾波器的寬度越大，但在低頻段引起的相位滯后也越大，而ξp的影響則相反。通過選擇ξp與ωp的值，既可使系統的頻率特性不發生較大改變，又能保證系統在濾波后具有較好的幅值裕度和相位裕度。

以某導彈一階彎曲振動模態為例，其結構阻尼比為0.05，根據發動機推進劑燃燒程度隨時間變化情況，設計結構濾波器主要參數的自適應規律具有如下形式：

(9)

其中，T01為主動段與被動段的時間分界點。

3 局部增益滑模控制器設計

在偽攻角反饋三回路自動駕駛儀中，引入局部增益滑模控制策略以抑制系統性能對指令幅值及其他干擾的靈敏度，同時考慮彈體彈性影響，可以得到控制結構如圖3所示。

控制系統設計時，可先確定剛性彈體的控制增益Id、K0與K4，并設計結構濾波器；然后引入局部增益滑模控制策略，利用切換函數，實現對加速度誤差積分增益的變結構控制。

圖3 導彈氣動伺服彈性滑模控制結構Fig.3 Topology of ASE sliding mode control for missile

3.1 控制增益自動優化

對于大包線飛行的戰術導彈而言，基于試錯原理的系統參數整定工作量較大，且存在不可避免的品質離散問題，不利于導彈性能潛力的充分發揮。為此，可采用極點配置理論[11]，對剛性彈體偽攻角反饋三回路自動駕駛儀進行優化設計。在舵控處斷開得到系統的開環傳遞函數為：

(9)

其中，

由此得系統的三階閉環傳遞函數為：

(10)

若將極點配置到由參數A、ω、ξ所決定的期望位置處，則有式(11)成立：

(s+A)(s2+2ξωs+ω2)=

s3+(Ba+Ida3-IdK4va5)s2+

(Ca+Ida3ωα+IdK0a3-IdK4va5a1)s+

IdK4va5Cz

(11)

推導可得控制增益為：

(12)

其中，共軛極點頻率為：

(13)

3.2 滑模控制策略設計

將阻尼回路與增穩回路等效為傳遞函數：

(14)

其中，

則等效控制結構如圖4所示。

圖4 等效控制結構Fig.4 Equivalent control structure

其中，c2>0,c1>0。

將系統動態約束方程代入切換面函數的一階導數整理可得：

(15)

選擇Lyapunov函數為：V(σ)=σ2/2。

在Lyapunov穩定性條件下有滑模控制策略：

(16)

針對切換面函數中角加速度信號可能帶來的噪聲問題，可采用濾波器對角速度和角加速度進行估計[12]，并定義等效切換面函數：

σeq=e-K6yωsynth

(17)

其中，

進一步整理可得實用的滑模控制策略為：

(18)

4 ASE控制技術仿真

氣動伺服彈性會使控制系統穩定性降低，加之多種非線性環節如舵系統間隙與飽和等因素影響，經常導致飛行狀態劇烈振蕩，甚至失控。因此，有必要在地面仿真試驗中集成ASE模型，如圖5所示，以檢驗控制系統的有效性。

圖5 非線性ASE仿真系統原理圖Fig.5 Schematic of nonlinear ASE simulation system

在飛行高度10km，速度2.0Ma，攻角20°的某特征點處，動力系數a2=16.9259，分別采用經典線性與滑模變結構方法，針對標稱模型進行控制設計，在a2向下攝動5倍的條件下進行仿真，結果如圖6所示。

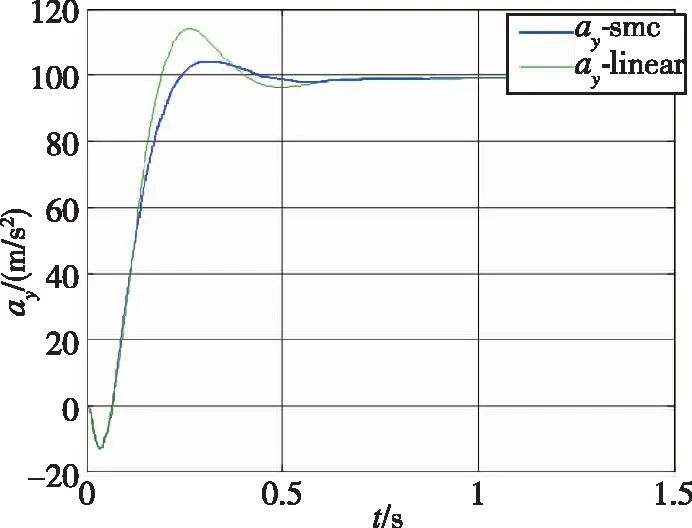
圖6 動力系數a2攝動條件仿真對比Fig.6 Simulation comparison with perturbation of dynamical coefficient a2

可見，帶有滑模變結構策略的控制系統性能明顯優于經典線性控制，在保持快速性的同時，超調與穩態品質優勢顯著，魯棒性更強。

對一條高度約為20km的高空彈道進行非線性仿真，與試驗結果的對比如圖7所示。

圖7 ASE仿真與試驗結果對比Fig.7 ASE simulation comparison with testing results

可見，對于長時振蕩現象，本文所提仿真方法能夠較為準確地復現時長。而且，采用離散傅氏變換的快速算法(Fast Fourier Transformation，FFT)技術對試驗數據進行頻譜分析，對比數字仿真ASE振蕩頻率偏差不大于0.5Hz，幅值吻合較好，且與典型ASE現象的持續時間基本吻合，滿足控制系統驗證對ASE仿真預測的要求，證明了在非線性仿真系統中集成彈體彈性模型是合理的。

為抑制ASE對高空彈道飛行狀態的不良影響，采用本文提出的自適應濾波與滑模控制技術進行數字仿真，結果如圖8與圖9所示。

圖8 姿態角速率仿真結果Fig.8 Simulation results of attitude rate

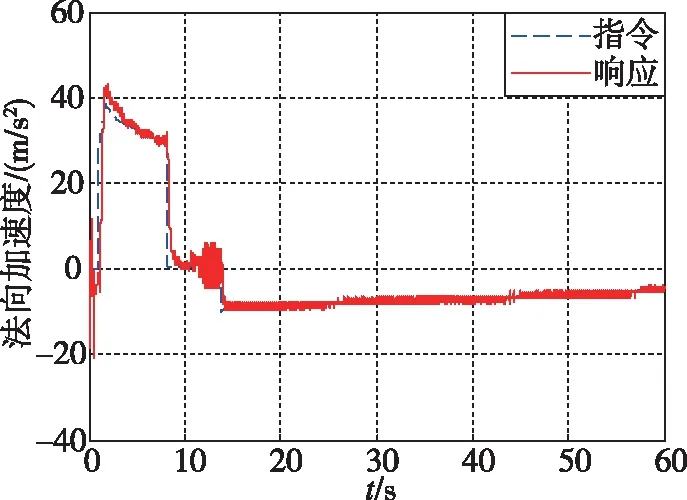
圖9 法向加速度仿真結果Fig.9 Simulation results of normal acceleration

由圖可知，采用自適應結構濾波與滑模控制技術，有效地抑制了ASE引起的高頻振蕩。全彈道飛行狀態變化平穩，彈性彈體穩定可控，過載跟蹤性能良好。

5 結論

本文所建立的彈性彈體模型能夠反映分布式氣動力、舵面慣性力與舵面氣動力等因素對飛行狀態的影響。

在非線性仿真系統中集成彈性彈體模型能夠有效預測、復現氣動伺服彈性引起的振蕩現象，便于飛行控制系統性能的深度校驗。

采用滑模變結構技術調整局部增益，能有效兼顧控制系統的動、靜態品質，并具有較強的魯棒性，從而獲得更優的綜合性能。