基于Hertz彈性接觸的船舶推進(jìn)軸系非線性校中計(jì)算

楊紅軍，李 俊，劉鎮(zhèn)劍

（上海船舶研究設(shè)計(jì)院，上海 201203）

0 引 言

大型或超大型遠(yuǎn)洋船舶多采用低速兩沖程柴油機(jī)作為推進(jìn)主機(jī)直接驅(qū)動(dòng)螺旋槳，推進(jìn)軸系承擔(dān)了從主機(jī)到螺旋槳傳遞功率和轉(zhuǎn)動(dòng)的功能。螺旋槳采用類似懸臂梁的安裝方式，導(dǎo)致尾管后軸承后端有很大的邊緣載荷，不利于尾管后軸承工作。近年來，由于船舶大型化以及對航行經(jīng)濟(jì)性的追求，一方面，主推進(jìn)功率越來越大；另一方面，推進(jìn)系統(tǒng)采用了更低轉(zhuǎn)速、更大直徑的螺旋槳，螺旋槳的重量也更大。螺旋槳重量的增加使得尾管后軸承的工作條件更加惡劣，軸系對溫度變化越來越敏感或船體變形導(dǎo)致軸承高度變化。在這種新的形勢下，由于軸系設(shè)計(jì)、安裝、使用不良等原因?qū)е碌奈补芎筝S承工作溫度升高、高溫報(bào)警，甚至燒損的事故案例，時(shí)有發(fā)生。

推進(jìn)軸系的校中是在靜止態(tài)下進(jìn)行計(jì)算、安裝、驗(yàn)證的，一個(gè)良好的靜態(tài)校中可以保證軸系在運(yùn)轉(zhuǎn)狀態(tài)下，軸承支承高度、軸承支反力、傾斜角度等指標(biāo)滿足相關(guān)要求，軸系可以可靠地工作。而良好的軸系安裝首先建立在良好的軸系校中計(jì)算的基礎(chǔ)上。

船舶推進(jìn)軸系校中計(jì)算本質(zhì)上是求解超靜定連續(xù)梁，求解方法通常有三彎矩法、傳遞矩陣法以及有限元法。在計(jì)算過程中，一般選取軸承的中點(diǎn)位置作為支承點(diǎn)，但考慮螺旋槳的懸臂梁安裝方式，我國的船標(biāo)[1]推薦尾管后軸承支點(diǎn)距離軸承后端面1/7～1/3的軸承有效長度。

由于螺旋槳重量的增加，導(dǎo)致尾管后軸承的負(fù)荷增加。為了降低尾管后軸承的名義壓力，需要適當(dāng)增加軸承的長度。但是，在螺旋槳重量的作用下，尾軸存在一定的撓度和轉(zhuǎn)角，過大的撓度和轉(zhuǎn)角值使得軸系在工作過程中，軸表面和軸承表面不能很好地貼合，產(chǎn)生較大的局部面壓，不利于尾管后軸承的潤滑。因此，在通常情況下，為保證尾管后軸承和尾軸之間的貼合，尾管后軸承的中心線須傾斜安裝，中國船級(jí)社規(guī)定在尾管后軸承的支點(diǎn)處，尾管后軸承和尾軸的相對傾角，在靜態(tài)下不超過3.5×10-4rad。通常，名義許用比壓被用于衡準(zhǔn)軸承工作，但它不能很好地反映軸表面和軸承表面的貼合情況，需要引入更多的指標(biāo)來指導(dǎo)船舶軸系校中計(jì)算，如日本船級(jí)社提出了尾管后軸承局部最大面壓的要求[2]。為改善尾管后軸承的潤滑，業(yè)內(nèi)提出了雙傾斜尾管后軸承的設(shè)計(jì)，但是傳統(tǒng)的單支點(diǎn)的計(jì)算處理方法已經(jīng)不能很好地給出設(shè)計(jì)方案。

國內(nèi)的主機(jī)廠、船舶設(shè)計(jì)所、船廠大都引進(jìn)了挪威船級(jí)社（DNV）NAUTICUS MACHINERY軟件的校中模塊，該模塊可根據(jù)DNV規(guī)范中尾管后軸承潤滑標(biāo)準(zhǔn)[3]，將尾管軸承簡化為兩個(gè)或三個(gè)支點(diǎn)，根據(jù)各支點(diǎn)的載荷大小來設(shè)置尾管后軸承的傾斜。法國船級(jí)社提出了“ESA”彈性校中的船級(jí)符號(hào)[4]，并配以其開發(fā)的Lilas彈性校中軟件。該軟件考慮了尾軸與尾管后軸承的彈性接觸，多次應(yīng)用到我國建造的高附加值船上。國內(nèi)，張敏等人[5]研究了水潤滑尾管后軸承多點(diǎn)非線性彈性支承計(jì)算模型的建立方法，將尾軸承沿長度方向分成N個(gè)分軸承，并假設(shè)每個(gè)分軸承剛度相等，為原軸承的1/N。然而，每個(gè)分軸承的支承剛度卻和載荷以及實(shí)際接觸情況有關(guān)，并不相等，但是，這種假設(shè)簡化了計(jì)算。

船舶推進(jìn)軸系中，尾管后軸承和尾軸的接觸計(jì)算具有邊界非線性特點(diǎn)，主要是由于尾管后軸承是長軸承，接觸范圍取決于螺旋槳重量、槳軸直徑、軸承和螺旋槳的相對位置以及軸承的傾斜情況，事先是未知的，因此需要在計(jì)算過程中進(jìn)行判斷、搜尋。使用平面梁單元對第二代四十萬噸礦砂船推進(jìn)軸系進(jìn)行建模，建立軸系校中有限元模型；同時(shí)將尾管后軸承等分成多個(gè)軸承段，使用Hertz接觸理論對各個(gè)軸承段進(jìn)行受力分析，計(jì)算接觸位移、接觸力和接觸剛度等參數(shù)；對有限元模型和軸承段的接觸模型進(jìn)行迭代求解，得到尾管后軸承和尾軸的接觸情況。

1 船舶推進(jìn)軸系的有限元模型

1.1 梁單元的剛度矩陣

在結(jié)構(gòu)力學(xué)中，通常將承受橫向力和彎矩的桿件稱為梁。假設(shè)不考慮梁的剪切應(yīng)變，可以用歐拉—伯努利梁假設(shè)，即忽略剪切應(yīng)變，假設(shè)變形前垂直梁中心線的截面，變形后仍然為平面，且仍然垂直中心線。如圖1所示的平面歐拉—伯努利梁單元，其結(jié)點(diǎn)為i和j上所受橫向力和彎矩，分別是Fi、Mi和 Fj、Mj，對應(yīng)結(jié)點(diǎn)位移為 νi、θi和 νj、θj。

根據(jù)有限元方法的基本原理，單元的位移模式具備完整性和協(xié)調(diào)性，因此單元的橫向位移和轉(zhuǎn)角是連續(xù)的。可將單元的結(jié)點(diǎn)位移表示成一定的多項(xiàng)式形式，就可以進(jìn)行單元的力學(xué)特性分析，得到作用在單元上結(jié)點(diǎn)力和結(jié)點(diǎn)位移之間的關(guān)系，并根據(jù)最小勢能原理，求得單元的剛度矩陣，如下式所示：

式中：E是材料的彈性模量，I是截面慣性矩，l為單元長度。

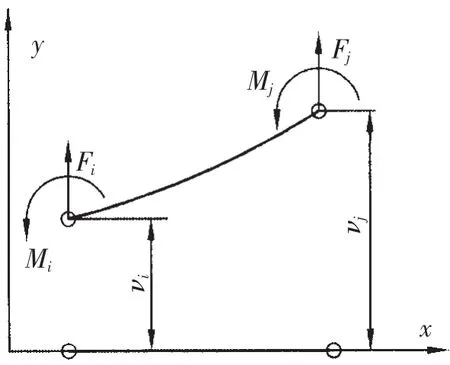
圖1 平面梁單元Fig.1 Model for plane beam element

在推導(dǎo)梁單元?jiǎng)偠染仃嚭陀?jì)算等效結(jié)點(diǎn)載荷時(shí)，采用的是局部坐標(biāo)系，將單元的剛度矩陣和等效結(jié)點(diǎn)力轉(zhuǎn)移到實(shí)際結(jié)構(gòu)坐標(biāo)系的對應(yīng)值后，就可以進(jìn)行總剛度矩陣和節(jié)點(diǎn)力向量的組裝。最后得到了整個(gè)結(jié)構(gòu)的平衡方程

式中：K為總剛度矩陣，δ為節(jié)點(diǎn)位移向量，f為節(jié)點(diǎn)力向量。

1.2 邊界條件的處理

由于整體剛度矩陣在組裝時(shí)，沒有考慮整體結(jié)構(gòu)的平衡條件，所以得到的整體剛度矩陣是一個(gè)奇異矩陣，只有在引入邊界約束條件后，對所建立的平衡方程（2）做適當(dāng)修改，才能根據(jù)方程組的具體特點(diǎn)，選擇適當(dāng)?shù)挠?jì)算方法求得節(jié)點(diǎn)位移。繼而求出單元的應(yīng)變和應(yīng)力。值得注意的是，引入邊界條件，修改平衡方程，實(shí)質(zhì)上就是消除結(jié)構(gòu)的剛體位移。

對于位移約束條件可以使用劃行列的方法。但對于如圖2所示的彈性支承，假設(shè)沿著梁第i自由度有位移約束ai，且彈性支承的剛度為Ci，根據(jù)最小勢能原理，只需對總剛度矩陣中對應(yīng)自由度的對角元素和節(jié)點(diǎn)力載荷向量中對應(yīng)自由度的元素進(jìn)行修改[6]，如下式所示：

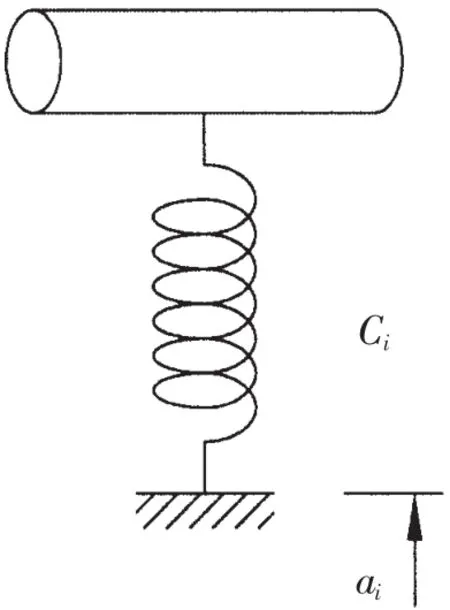
圖2 彈性支承示意Fig.2 Sketch for elastic support

2 軸和軸承的接觸模型

Hertz接觸理論是根據(jù)完全彈性體的靜態(tài)接觸條件提出的，可用來計(jì)算曲面接觸副的彈性變形和應(yīng)力場。Hertz接觸模型基于如下的假定：①接觸區(qū)域?yàn)榫鶆虿牧希l(fā)生接觸時(shí)未超過屈服應(yīng)力；②接觸應(yīng)力沿著接觸切平面的法線，即接觸體之間不存在切向力；③接觸面積要小于接觸體的尺寸；④接觸體處于自由平衡狀態(tài)；⑤不考慮接觸面的粗糙度。如圖3所示的兩圓柱的圓心在接觸點(diǎn)同一側(cè)，RA和RB分別為兩圓柱的半徑，且RA＜RB，2×len為圓柱長。兩相同長度的彈性圓柱在載荷W作用下，發(fā)生擠壓，接觸線擴(kuò)展成一個(gè)狹長的面，其半寬為b。則接觸半寬，最大面壓和接觸變形可由以下公式進(jìn)行計(jì)算[7]。

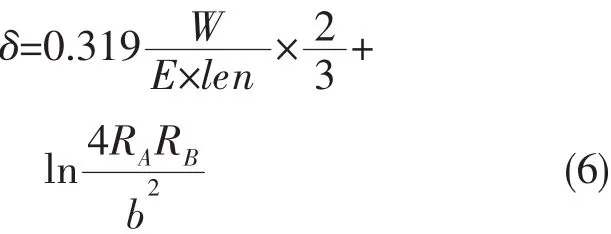
在傳統(tǒng)的船舶推進(jìn)軸系校中計(jì)算中，通常將尾管后軸承，簡化為一個(gè)支點(diǎn)，用軸承的名義比壓以及支點(diǎn)處尾管后軸承與螺旋槳軸的相對傾角來衡準(zhǔn)計(jì)算結(jié)果。由于尾軸自身存在撓度變形，軸的中心和軸承中心并不平行，軸和軸承之間存在很大的邊緣載荷，部分區(qū)域的軸承壓力較大。為了對尾管后軸承的實(shí)際工作進(jìn)行更好的模擬，我們把尾管后軸承分成多段，如圖4所示。這樣可以很好地模擬軸表面和軸承表面之間的帖合情況。

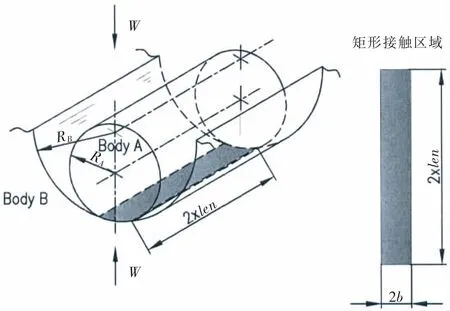
圖3 兩平行彈性圓柱的接觸模型Fig.3 Contact model between two parallel elastic cylinders

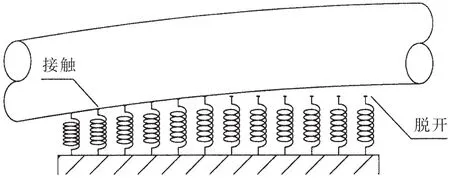
圖4 尾管后軸承多段支承示意Fig.4 Multi-support for after stern tube bearing

在計(jì)算過程中，首先根據(jù)尾管后軸承分支點(diǎn)初始位移判斷軸承段和相應(yīng)軸段是否存在接觸，使用Hertz接觸模型求解接觸力和接觸剛度，然后求解有限元模型，判斷結(jié)果是否收斂，如果不收斂就調(diào)整支點(diǎn)高度，進(jìn)行下一步計(jì)算，具體流程如圖5所示。

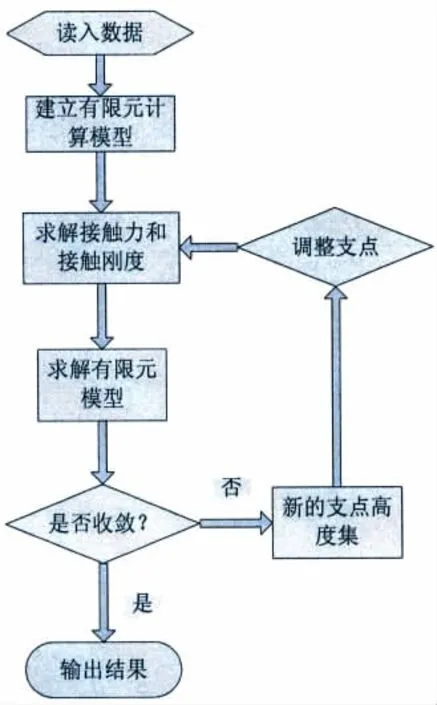
圖5 計(jì)算流程圖Fig.5 Flow chart for calculation

3 算 例

3.1 計(jì)算模型

第二代四十萬噸礦砂船，使用7S80MEC9主機(jī)，直接驅(qū)動(dòng)螺旋槳，其推進(jìn)軸系校中計(jì)算模型如圖6所示。尾管后軸承后端面定位于2 927 mm，前端面定位于4 737 mm，尾管前軸承使用單支點(diǎn)彈性支承模型，具體定位是9 057 mm處。

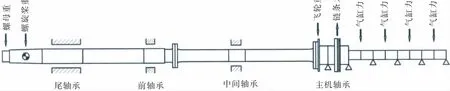
圖6 軸系校中計(jì)算模型Fig.6 Model for shaft alignment calculation

3.2 計(jì)算結(jié)果與分析

首先對尾管后軸承單支點(diǎn)模型進(jìn)行了計(jì)算，并假定尾管后軸承支點(diǎn)距尾管后軸承的后端面的距離為四分之一的軸承有效長度，各軸承負(fù)荷如表1的第1行所示，尾管后軸承支點(diǎn)處的轉(zhuǎn)角為0.53 mrad，根據(jù)該轉(zhuǎn)角值，我們采用尾管后軸承中心0.4 mrad和0.53 mrad的單傾斜方案，以及0.55/0.4 mrad和0.7/0.5 mrad的雙傾斜方案進(jìn)行計(jì)算。雙傾斜的斜率轉(zhuǎn)折點(diǎn)在尾管后軸承的中點(diǎn)處。圖7為0.55/0.4 mrad雙傾斜軸承示意，L為總長，軸瓦后半段與水平線的夾角是0.55 mrad，軸瓦前半段與水平線的夾角是0.4 mrad。軸承負(fù)荷如表1所示。在軸系支點(diǎn)高度相同的情況下，不同的尾管后軸承的傾斜設(shè)定只影響尾管前后軸承的負(fù)荷，中間軸承和主機(jī)軸承影響較小。將尾管后軸承分成20等份，使用Hertz接觸理論計(jì)算每一段軸承和軸的接觸力學(xué)特性。尾管后軸承與軸的接觸范圍如圖8～11所示。

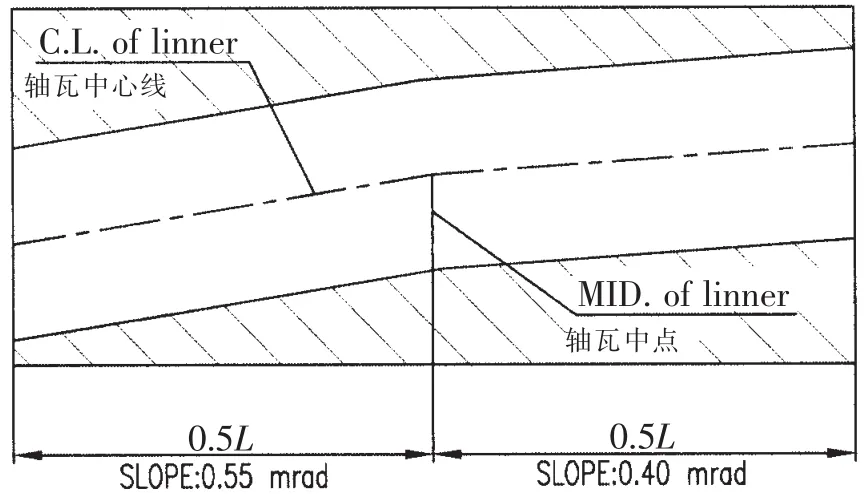
圖7 0.55/0.4 mrad雙傾斜示意Fig.7 Sketch for SLOPE 0.55/0.4 mrad

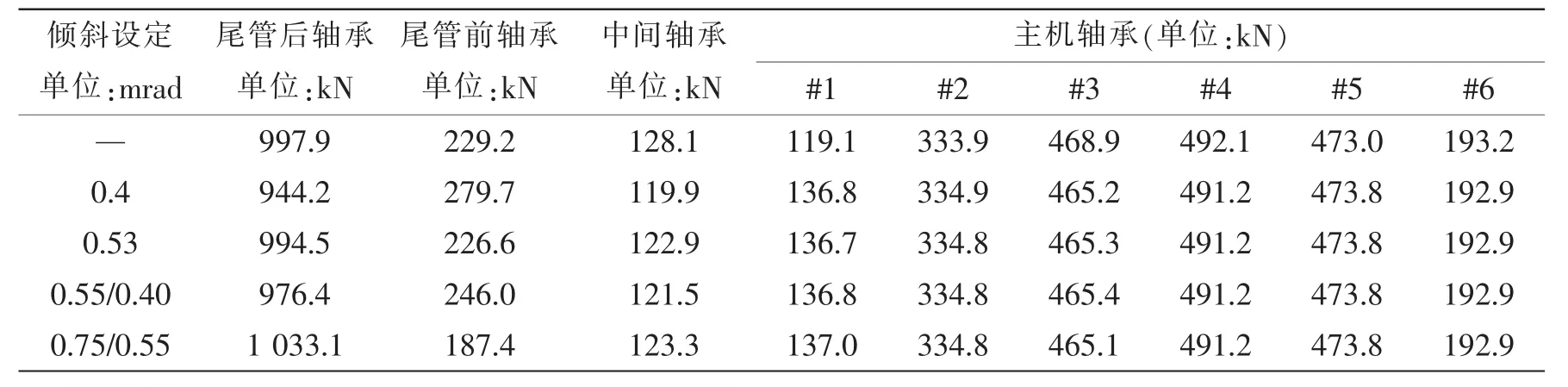
表1 各計(jì)算工況下軸承負(fù)荷Tab.1 Bearing loads for each calculation condition

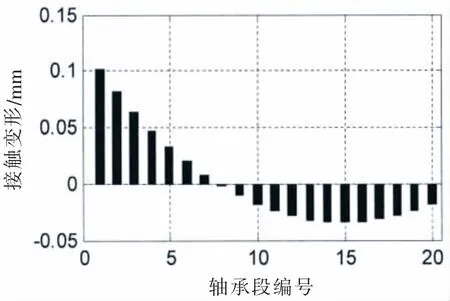
圖8 （a） 接觸變形@SLOPE 0.4 mradFig.8(a)Contact deformation@SLOPE 0.4 mrad

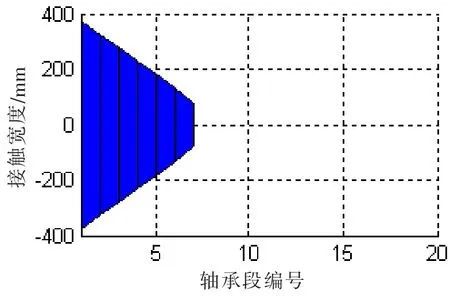
圖8 （b）接觸寬度@SLOPE 0.4 mradFig.8(b)Contact width@SLOPE 0.4 mard

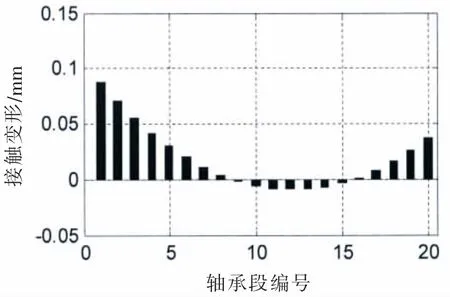
圖9 （a） 接觸變形@SLOPE 0.53mrad Fig.9(a)Contact deformation@SLOPE 0.53mrad

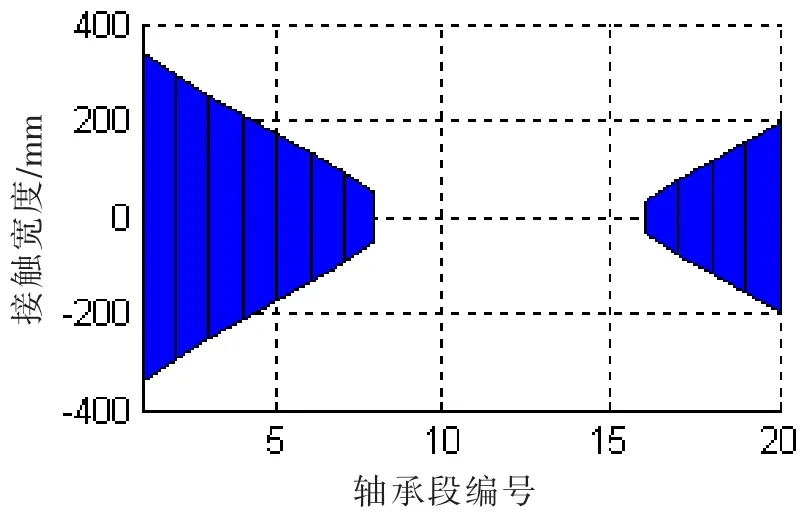
圖9 （b）接觸寬度@SLOPE 0.53mradFig.9(b)Contact width@SLOPE 0.53mard

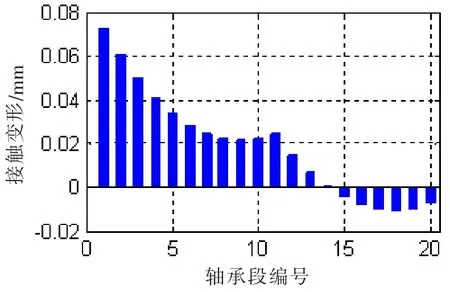
圖10 （a） 接觸變形@SLOPE 0.55/0.4 mradFig.10(a)Contact deformation@SLOPE 0.55/0.4mrad

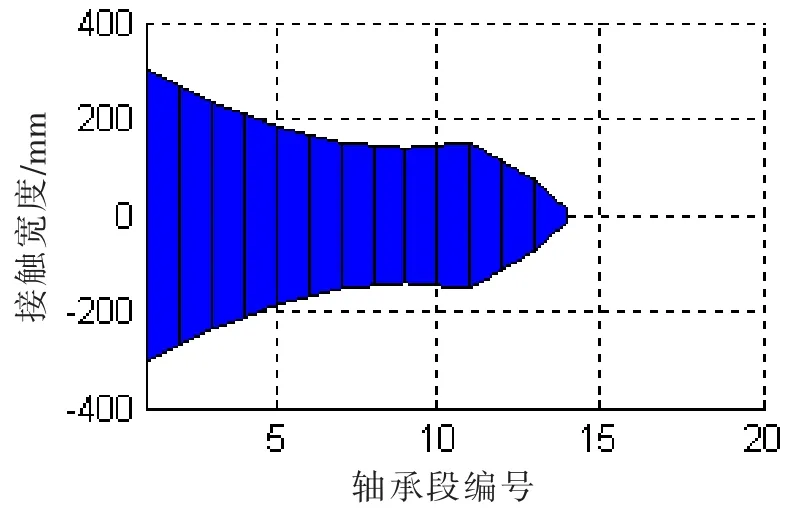
圖10 （b）接觸寬度@SLOPE0.55/0.4 mradFig.10(b)Contact width@SLOPE 0.55/0.4mard

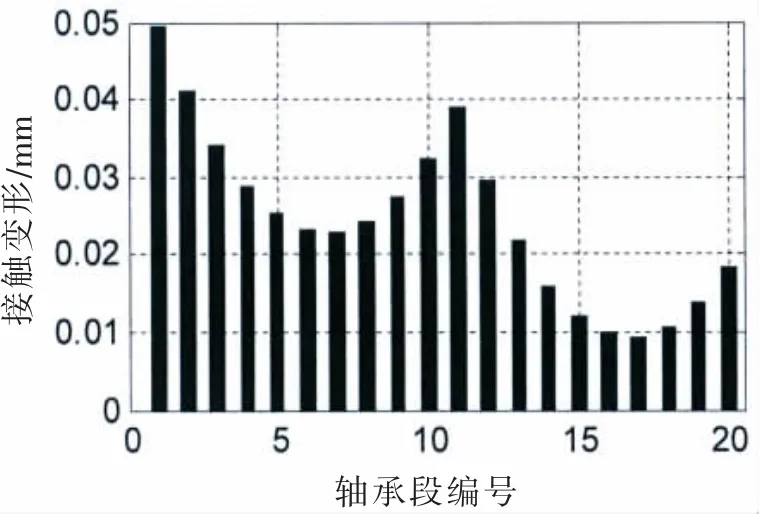
圖11 （a） 接觸變形@SLOPE 0.7/0.5 mradFig.11(a)Contact deformation@SLOPE 0.7/0.5 mrad

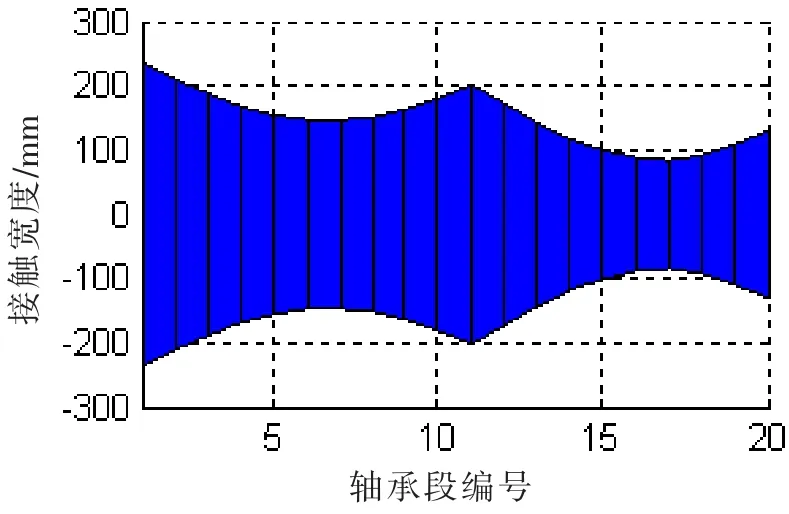
圖11 （b）接觸寬度@SLOPE0.7/0.5 mradFig.11(b)Contact width@SLOPE 0.7/0.5 mard

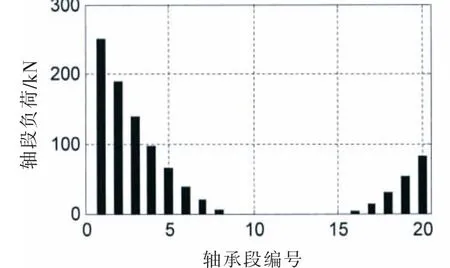
圖12 （a）軸承段負(fù)荷@SLOPE 0.53 mradFig.12(a)Bearing load@SLOPE 0.53 mrad

圖12 （b）接觸剛度@SLOPE 0.53 mradFig.12(b)Contact stiffness@SLOPE 0.53 mard

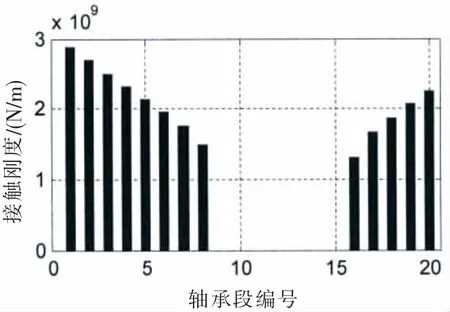
圖12 （c）最大接觸壓力@SLOPE 0.53 mradFig.12(c)Max contact pressure@SLOPE 0.53 mard

在接觸變形圖中，X軸以上柱狀圖高度為正，表征接觸變形量δ，X軸以下的柱狀圖高度為負(fù)，表征軸和軸承之間的間隙。在不同的尾管后軸承中心傾斜條件下，接觸變形和接觸區(qū)域是不同的。各個(gè)軸承段的最大接觸變形小于0.1 mm，而尾管軸承的白合金厚度為3 mm；只有在0.7/0.5 mrad的雙傾斜狀態(tài)下，軸和軸承在長度方向是完全接觸的。更大的接觸范圍，可以獲得較小的接觸壓力，在軸系運(yùn)轉(zhuǎn)時(shí)，更容易形成油膜，延長尾管后軸承的工作壽命。在計(jì)算得到接觸變形和接觸范圍后，可以方便地得到Hertz接觸力，即軸承段的負(fù)荷，以及最大接觸壓力和接觸剛度。以0.53 mard的單傾斜和0.55/0.4 mrad雙傾斜為例，其計(jì)算結(jié)果如圖12和13所示。

圖13 （a）軸承段負(fù)荷@SLOPE 0.55/0.4 mradFig.13(a)Bearing load@SLOPE 0.55/0.4 mrad

圖13 （b）接觸剛度@SLOPE 0.55/0.4 mradFig.13(b)Contact stiffness@SLOPE 0.55/0.4 mard

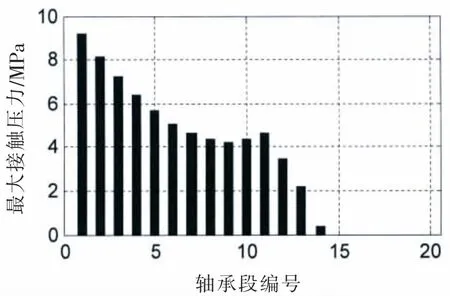
圖13 （c）最大接觸壓力@SLOPE 0.55/0.4 mradFig.13(c)Max contact pressure@SLOPE 0.55/0.4 mard

對比圖12和圖9，圖13和圖10，軸承段負(fù)荷的柱狀圖和接觸變量的柱狀圖的形狀是比較一致的，軸承段負(fù)荷和接觸變形量基本呈正相關(guān)。接觸剛度的柱狀圖高度相對較均勻，接觸剛度在109N/m量級(jí)，和文獻(xiàn)[8]內(nèi)容基本一致。由計(jì)算結(jié)果可知，四種計(jì)算工況，結(jié)合表一中的尾管后軸承負(fù)荷，在較小的尾管后軸承傾斜設(shè)定下，軸承和軸的接觸區(qū)域主要在軸承的后邊緣或者后半部分；在較大的單傾斜設(shè)定下，在軸承的前后端軸承和軸都有接觸，因此大傾斜設(shè)定的尾管后軸承的等效支點(diǎn)相對靠前一些，導(dǎo)致尾管后軸承負(fù)荷增加。

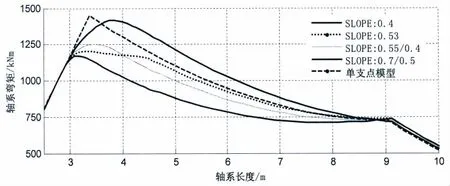
圖14 尾管前后軸承之間的軸系彎矩圖Fig.14 Moment curve between after and forward s/tube bearing

圖14為尾管前后軸承之間的彎矩圖，由于螺旋槳最末端、中間軸以及曲軸上的彎矩計(jì)算結(jié)果基本相同，圖中僅僅顯示了尾管前后軸承之間軸系上的彎矩。對于尾管后軸承的單支點(diǎn)模型計(jì)算結(jié)果，由于尾管后軸承支反力很大，使得在支點(diǎn)處剪力改變了符號(hào)，因此，支點(diǎn)處的彎矩存在轉(zhuǎn)折點(diǎn)。但對于尾管后軸承多點(diǎn)支承的非線性模型，支點(diǎn)是通過實(shí)際的軸承中心傾斜情況計(jì)算搜索得到的，且是多個(gè)分支點(diǎn)共同起作用，分支點(diǎn)的支反力逐漸使剪力改變符號(hào)，彎矩曲線開始下降，因此尾管后軸承處彎矩曲線是近似圓弧過度；對于較小的尾管后軸承傾斜，軸承和軸的接觸位于后端，彎矩的峰值較低，而較大的尾管后軸承傾斜，使得彎矩峰值較高，較前者升高將近20%，也使得螺旋槳軸上的彎曲應(yīng)力也升高將近20%，影響很大。如中國船級(jí)社規(guī)定螺旋槳軸上的最大彎曲應(yīng)力不得超過20 MPa。由于軸承傾斜設(shè)置不同，軸系撓度曲線也有差別，圖15為軸系末端到尾管后軸承的撓度曲線，0.4 mrad的SLOPE撓度最小，0.7/0.5 mrad撓度最大。

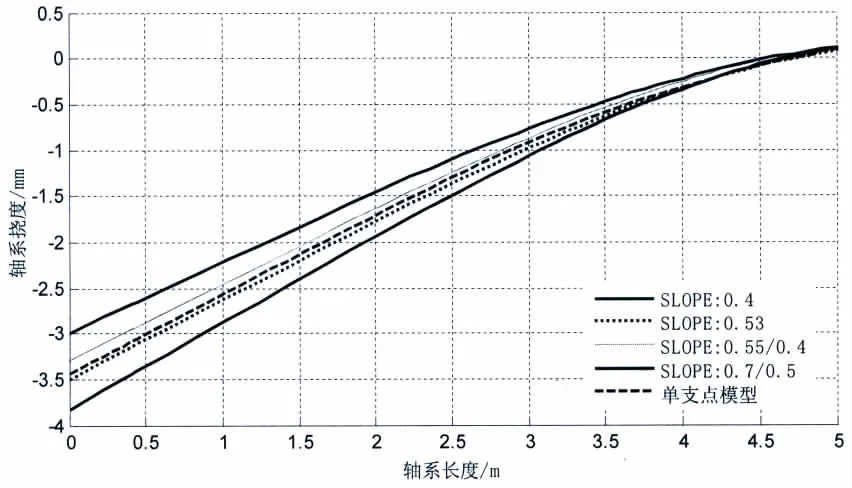
圖15 軸系末端到尾管后軸承的撓度曲線Fig.15 Deflection curve from end of shaft to after s/tube bearing

4 結(jié) 論

（1）將尾管后軸承等分成多個(gè)軸承段，用Hertz彈性接觸模型描述軸承和軸的接觸力學(xué)特性，結(jié)合平面梁單元的軸系校中計(jì)算有限元模型，可以獲得尾管后軸承和軸的接觸范圍、接觸變形、接觸最大面壓、接觸剛度等計(jì)算結(jié)果。這些是尾管后軸承單支點(diǎn)計(jì)算模型無法達(dá)到的。

（2）根據(jù)軸承段的最大接觸壓力以及軸承段負(fù)荷等結(jié)果，可以更好地設(shè)置尾管后軸承的傾斜。保證軸系運(yùn)轉(zhuǎn)時(shí)尾管后軸承和軸有較好的貼合，同時(shí)可以防止軸和軸承之間過大的接觸壓力，以及在軸系啟動(dòng)運(yùn)轉(zhuǎn)時(shí)可能會(huì)導(dǎo)致白合金的擦傷或者剝落。

（3）尾管后軸承的支點(diǎn)位置不用在計(jì)算前假定，而是由多個(gè)分支點(diǎn)承擔(dān)。根據(jù)實(shí)際的軸承中心傾斜情況，由計(jì)算結(jié)果軸段負(fù)荷的分布情況來確定。且軸承的支承剛度也可以根據(jù)計(jì)算結(jié)果確定，不需事先假定。