中間約束軸向運動梁橫向非線性振動

趙小穎, 李 彪, 丁 虎, 陳立群,3

(1. 上海大學 上海市應用數學和力學研究所, 上海 200072;2. 上海衛星工程研究, 上海 200240; 3. 上海大學 力學系, 上海 200444)

作為航天工程、機械生產、日常生活中常見的沿著軸向移動的柔性連續體體的力學模型，自20世紀60年代Mote院士提出動力學模型[1]以來，軸向運動梁已經得到廣泛的研究。基于不同工況下的軸向運動梁，橫向自由振動頻率得到了研究[2-5]。也有研究人員關注于受到外部激勵的軸向運動梁的振動特征研究[6-8]。Marynowski等[11]綜述了2014年以前軸向運動彈性振動相關的研究進展。

有很多工況需要在軸向運動梁中部添加彈性支撐或者約束，例如，空中纜車的纜繩，為了增加剛度，會增加支撐；再如，為了抑制軸向運動系統的橫向振動，會在系統中間彈性吸振裝置，等等。盡管對于包含中間彈性約束的柔性體已經得到廣泛的研究[10-13]，但是對于中間彈性約束影響軸向運動系統動力學特征的研究并不多見。Ghayesh[14]研究了中間黏彈性約束對軸向運動弦線的非線性振動特性的影響，包括周期響應與分岔混沌特征。Zhang等[15]研究了軸向運動梁在初始激勵作用下，非線性吸振器對系統的暫態振動的吸收效果，證明非線性吸振器的優異吸振效果。需要說明的是，以上提到的文獻都是基于Galerkin截斷方法的研究結果，對于中間約束的軸向移動柔性體，移動速度對約束的作用效果的影響、截斷階數的收斂性都沒有做出說明。目前，還缺乏對軸向運動速度和中間彈性支撐或者約束相互影響的研究。

本文運用Galerkin截斷方法研究了在兩端簡支邊界條件下，中間彈簧剛度、軸向運動速度、不同截斷階數對軸向運動梁固有振動頻率的影響，并通過對比，給出了收斂的假設模態截斷階數。另外，本文還研究了中間彈簧剛度、軸向運動速度對穩態響應的影響。數值結果表明，中間彈性約束對軸向移動梁振動有著復雜影響，沿著軸向運動的速度會增加中間約束對梁自由振動頻率和受迫振動響應影響的復雜性。

1 數學模型和控制方程

圖1所示為帶有中點約束的軸向運動梁力學模型，在距離梁左邊界xs處加上了彈簧支撐，剛度系數為k。其中ρ為軸向運動梁的質量密度，A為橫截面面積，E為彈性模量，I是關于中性軸的截面慣性矩，EI為梁的彎曲剛度，P0是梁的初始軸向張力。梁以固定速度Γ沿著其軸向運動，梁長為L。

圖1 軸向運動梁物理模型

軸向運動梁的動能T和勢能U的表達式分別為

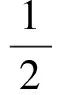
(w,t+Γw,x)2}dx

(1)

(2)

式中：w(x,t)是梁的橫向位移，u(x,t)是梁的徑向位移，t是時間坐標，δ(x)表示狄拉克函數，式(1)第一項為軸向運動梁與縱向運動有關的動能，第二項為軸向運動梁與橫向運動有關的動能。式(2)第一項是與軸力P0有關的勢能，第二項是中性面拉伸產生的勢能，第三項是與曲率有關的勢能，最后一項是與中點約束彈簧有關的勢能。根據Hamilton變分原理，有

(3)

隨時間簡諧變化的分布力所做虛功為

(4)

由此可以得到如下控制方程

ρA(w,tt+2Γw,xt+Γ2w,xx)-

EIw,xxxx-P0w,xx+δ(x-xs)(kw)=

F(t)cos(ωt)

(5)

ρA(u,tt+2Γu,xt+Γ2u,xx)-

EA(u,xx+w,xw,xx)=0

(6)

因為縱向位移比橫向位移小很多，并且EA>>ρA，所以可以得到

u,xx+w,xw,xx=0

(7)

由上式可以得到

(8)

其中，C1(t)和C2(t)是關于時間t的函數。

兩端簡支邊界縱向邊界條件為

u(0,t)=0,u(L,t)=0

(9)

將式(8)代入式(9)得到

(10)

將式(10)代入式(5)得到

ρA(w,tt+2Γw,xt+Γ2w,xx)+

EIw,xxxx-P0w,xx+kwδ(x-xs)-

(11)

兩端簡支邊界橫向邊界條件為

w(0,t)=w(L,t)=0,

w,xx(0,t)=w,xx(L,t)=0

(12)

通過無量綱化得到控制方程

w,tt+2γw,xt+(γ2-1)w,xx+kwδ(x-xs)+

F(t)cos(ωt)

(13)

無量綱參數定義如下

(14)

無量綱簡支邊界條件為

w(0,t)=w(1,t)=0,

w,xx(1,t)=w,xx(0,t)=0

(15)

2 Galerkin截斷

設式(13)的解為

j=1,2,…,M

(16)

將(16)式代入控制方程后得到

(17)

假定，上面等式等號左邊的式子等于RM(x,t)，式RM(x,t)應滿足

i=1,2,…,M

(18)

即可實現對控制方程的M階Galerkin截斷，最終將方程轉化為含有M個未知數為qj(j=1,2,…,M)的常微分方程組。將中間彈簧設置在xs=L/2處。

計算自由振動頻率時，忽略上式中的非線性，通過無量綱化得到控制方程

w,tt+2γw,xt+(γ2-1)w,xx+

(19)

對于給定的軸向速度、中間剛度系數和截斷階數，通過廣義本征值問題，即可求得前M階固有頻率。

3 固有頻率

下面取8階Galerkin截斷(M=8)。取梁的長度L=0.3 m,楊氏模量E=200 MPa，初始張力P0=80 N，ρ=1 200 kg/m3，梯形截面上底寬0.022 m，下底寬0.008 9 m，高度0.018 m，kf=0.442 8。圖2給出了前兩階固有頻率隨速度變化曲線。從上圖可以看出，前兩階固有頻率隨著中間彈簧剛度的增加不斷增大，圖2(a)中清楚的顯示當無量綱約束剛度超過35以后，梁的軸向臨界速度不再變化。圖2(b)表明，當軸向運動速度為零時，第二階固有頻率不受中點約束的影響。但是隨著速度的增大，約束剛度對第二階固有頻率的影響變得越發顯著。更加有趣的是，當無量綱約束剛度取值大于200時，在運動速度不大時，第二階固有頻率會隨速度增大而增大。

圖3給出了速度對不同剛度下軸向運動梁前兩階橫向振動固有頻率的影響。從圖(a)和(b)中可以看出，當軸向運動速度為零時，第二階固有頻率開始不隨中點約束剛度變化，而第一階頻率持續增大。但是當無量綱約束剛度增大到220左右時，第一階頻率超過第二階頻率。最初的第二階模態對應的頻率成為最小的頻率，即基頻，最初的第一階模態對應的頻率不再是最小的頻率，成為第二階頻率，繼續增大。這一前兩階頻率轉換的現象同樣發生在軸向運動速度不為零的工況。另外，還需要說明的是，軸向運動的速度會使得中間彈簧無量綱剛度系數小于200時梁的第二階固有頻率受到中點約束彈簧的影響。如圖所示，速度為零時，此時的第二階固有頻率不隨中間約束剛度變化。因此可以判定，軸向移動的速度使得原本中點對稱的模態，不再對稱。

圖4比較了不同截斷階數對前兩階固有頻率的影響。截斷階數分別取M=4、8、16和24階，中間彈簧無量綱剛度系數k取200。對于前2階固有頻率的預測，4種截斷階數給出了相同的變化趨勢。8、16和24階截斷對應的第一階固有頻率基本重合。相比之下，4截斷的結果與8、16、24階截斷結果的差別隨固有頻率的階數增大而增大，第一階和第二階固有頻率間，有可識別的差別。

(a) 第一階固有頻率

(b) 第二階固有頻率

(a) 第一階固有頻率

(b) 第二階固有頻率

(a) 第一階固有頻率

(b) 第二階固有頻率

4 穩態響應

取無量綱阻尼系數μ=1.161 3，無量綱外激勵F=0.3，其他參數與圖2一致。

圖5(a)為軸向運動梁在距離左端1/4點處的穩態響應曲線。通過觀察發現，速度的變化對曲線有著明顯的影響。既改變軸向運動梁橫向受迫振動的共振區，也改變梁的共振幅度。圖5(b)通過改變中間彈簧約束的剛度值發現，在一定范圍內，隨著剛度k的增加，軸向運動梁前兩階共振逐漸接近。另外，軸向運動速度的增大和中間約束的減小，梁的振動幅度都會增大，而且非線性跳躍的區域也都會隨著增大。

(a) 穩態響應(k=100)

(b) 穩態響應(γ=0.5)

5 結 論

本文運用Galerkin截斷方法，研究了帶有中間約束的軸向運動梁的橫向非線性振動。得到了不同中間約束剛度系數下，軸向運動速度與頻率的變化關系曲線以及穩態響應曲線，分析了不同變化因素對固有頻率及穩態響應曲線的影響以及研究方法的收斂性。研究揭示了中間彈性約束和軸向運動速度的共同作用對梁固有頻率及穩態響應的復雜影響。發現中間約束剛度的增加會導致軸向運動梁的固有頻率不同程度的增加，盡管中間約束對靜態梁偶數階模態無影響。更有意思的是，約束剛度的增加會使得前兩階模態的頻率相互轉換。另外，還發現4階Galerkin截斷的計算結果與高階截斷相比較，存在可以辨識的誤差。而在橫向非線性受迫振動方面發現，軸向運動速度和中間彈性約束剛度的影響會有疊加效應，兩個因素的共同作用下，梁的穩態響應會產生復雜的變化趨勢。