兩法解決平衡的穩定性問題

(紹興市第一中學,浙江 紹興 312000)

物體的平衡狀態可分為穩定平衡、不穩定平衡和隨遇平衡.在高中物理競賽教學中，經常要求求解物體的平衡位置，并對其平衡的穩定性進行分析討論.對于這類問題，一般可以用以下兩種方法進行求解.

1 力矩法

處于平衡狀態的物體，若受到外界擾動而偏離平衡位置，將產生合外力力矩.如果合外力力矩是一個回復力矩，即此合外力力矩有把物體拉回原平衡位置的傾向，那么物體的平衡為穩定平衡；如果合外力力矩有把物體推離平衡位置的傾向，那么物體的平衡為不穩定平衡；如果既沒有回復原位又沒有遠離原位的傾向，那么物體的平衡為隨遇平衡.

力矩法，即先通過力矩平衡找到平衡位置；再考慮偏離平衡位置后，偏移量的方向與所受合外力力矩的方向的關系，從而來判斷物體的平衡穩定性.

例題.如圖1所示，半徑為R的圓環繞其鉛垂直徑以不變的角速度ω勻速轉動.兩質量為m的珠子用長為L=R的輕桿相連，套在圓環上可以無摩擦地滑動.試求輕桿在圓環上的平衡位置，用環心O與桿中點C的連線與豎直軸的夾角θ表示，并分析平衡的穩定性.[1]

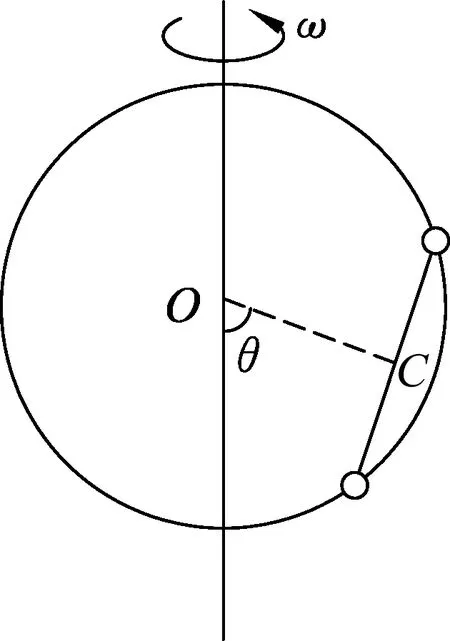
圖1 圖2

解析：(1) 先求輕桿在圓環上的平衡位置.

取隨環勻速轉動的參考系，輕桿與珠子組成的系統處于平衡狀態，系統受到重力2mg、環對兩小球指向環心的彈力N1、N2，以及慣性離心力f1、f2，受力分析如圖2所示，其中作用在上、下端珠子的慣性力f1、f2分別為

f1=mω2Rsin(θ+30°),

f2=mω2Rsin(θ-30°).

對豎直軸,系統所受合外力力矩為M=MG+Mf1+Mf2，其中

代入化簡可得

平衡時有M=0,解此方程,得系統平衡位置.

(2) 討論平衡位置的穩定性.

微擾令系統偏離平衡位置，討論偏移量dθ的正負與對應合外力力矩M的正負關系.若偏離平衡位置時，合外力力矩M一直為0，則為隨遇平衡；若偏離平衡位置的偏移量dθ的正負與合外力力矩M的正負一致，則為不穩定平衡；相反的，則為穩定平衡.

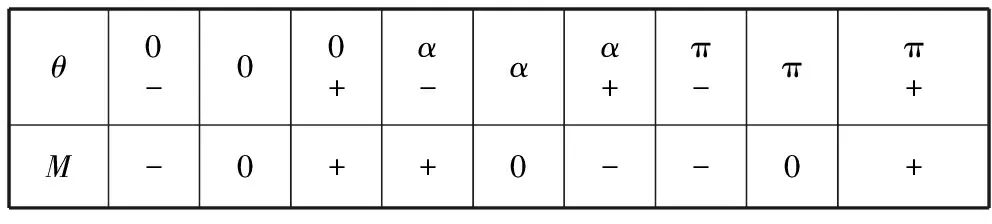
表1

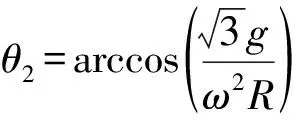
2 勢能函數法

下面用勢能函數法重解上述例題.

取隨環勻速轉動的參考系，輕桿與珠子組成的系統處于平衡狀態，通過受力分析可知，該例中系統的勢能包含重力2mg對應的重力勢能Epg、慣性離心力f1和f2對應的離心勢能Ef1及Ef2.

同理,下端的珠子的離心勢能為

其中,r1=Rsin(θ+30°),r2=Rsin(θ-30°).

從而有系統的勢能E(θ)=Epg+Ef1+Ef2,即

從圖中可知，勢能函數的極值點對應平衡位置，如圖3的A點和B點，圖4的C點、D點和E點；勢能函數的極大值位置對應不穩定平衡位置，如圖3的B點，圖4的C點和E點；勢能函數的極小值對應穩定平衡位置，如圖3的A點和圖4的D點.

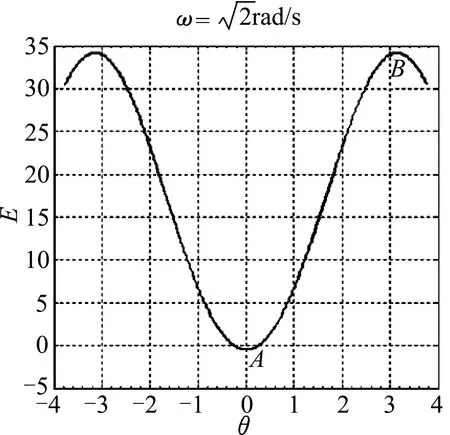
圖3 勢能函數圖

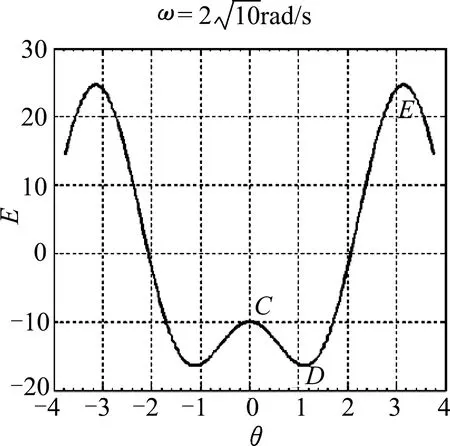
圖4 勢能函數圖

因此可以令勢能函數對廣義坐標的一階導數等于零，來求得平衡位置；然后利用勢能函數對廣義坐標的二階導數在平衡位置取值的正負來判斷平衡是屬于穩定平衡還是不穩定平衡.

結論與方法1一致.

為討論平衡位置的穩定性,計算勢能函數對廣義坐標的二階導數,有

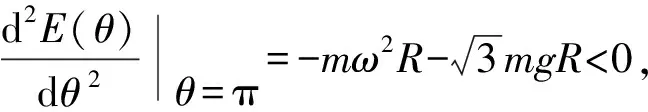
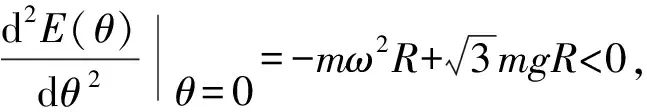
取極小值,屬于穩定平衡.

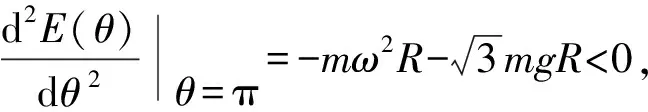
3 方法應用

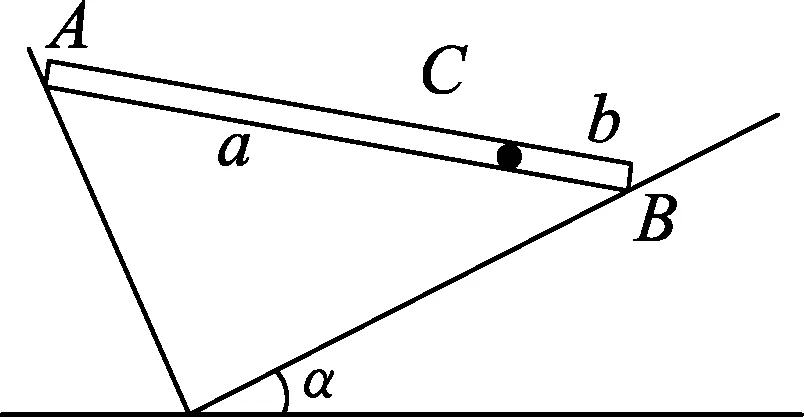
圖5

如圖5所示,桿長l=a+b,質心在C點,桿的A、B兩端分別支于互相垂直的兩個光滑斜面上而處于平衡.試求出桿的平衡位置,并分析平衡的穩定性.