基于ANFIS的水環境質量參數COD預測模型研究

潘 淼

(遼寧潤中供水有限責任公司，遼寧 沈陽 110000)

經濟社會的快速發展在大幅提升人們的生活水平的同時，也不可避免地造成了日趨嚴重的環境污染。為有效利用水資源，減少水質污染造成的負面影響，對水質進行科學、準確、可靠的評價以及對其變化趨勢進行有效預測極為重要[1]。網絡自適應模糊推理系統(ANFIS)實現了人工神經網絡技術和模糊控制技術的完美融合，可以在水質評價和預測領域發揮更要重要的作用[2]。

1 指標選取和數據預處理

1.1 水質指標選取

水環境質量通常是由多個水質指標數據體現出來的，而水環境質量預測也需要依據權威的水質監測數據創建預測模型。2003年，國家環保部出臺的HJ-T100- 2003《水質指標的自動分析儀技術》中提出了9項環境保護行業標準，不僅包含了總氮、總磷、氨氮、pH等傳統慣例監測項目，同時也包含了化學需氧量(COD)、生化需氧量(BOD)以及部分重金屬離子等水質監測參數。結合上述標準以及水質監測的實際需求，本次研究選取了水質監測站的COD、pH、溶解氧、氨氮和總磷等5個水質質量監測指標。其中，化學需氧量(COD)作為研究水域中還原性物質污染程度的主要指標，是進行水質預測的重要參數，因此將COD作為預測模型輸出計算的基本參數。

1.2 數據預處理

不同的水質參數擁有不同的量綱和單位，會對模型的數據分析造成影響，因此必須要對數據進行歸一化處理[3]。本次研究中擬采用如下的線性函數進行歸一化處理。

(1)

式中，xmin—某組數據的最小值；xmax—某組數據中的最大值。

在數據進行歸一化處理之后，試驗數據將映射在區間[0，1]之間。

在模型試驗過程中，對整體數據進行聚類分析，將其中的離群數據刪除，可以有效提升模型本身的預測精度。因此，結合數據的實際特征，采取歐式距離法對水質數據進行聚類分析[4]。

2 ANFIS預測模型的構建

2.1 模型預測方法

基于ANFIS水質預測模型的預測基本流程如圖1所示。

第一步，首先確定預測水域的主要參數，本次研究選取了水質監測站的COD、pH、溶解氧、氨氮和總磷等5個參數。第二步，對原始數據進行預處理：在剔除部分無效和離群數據后，將余下的數據進行歸一化處理，在歸一化處理之后進行測試和訓練樣本分組。第三步，利用訓練樣本對模型進行訓練，尋求并確定最合適的參數以及隸屬度函數。第四步，將測試數據輸入模型完成對COD水質參數的預測。

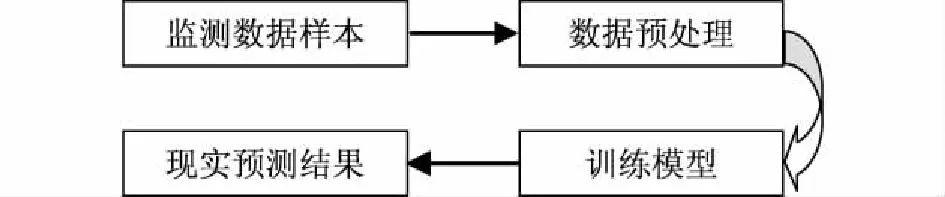
圖1 ANFIS水質預測模型的預測基本流程

2.2 隸屬度函數選取

在基于ANFIS的水質預測模型中，隸屬度函數類型的選取以及數目的確定對模型預測精度具有較大影響[5]。常見的隸屬度函數通常包括高速函數、鐘型函數、梯形函數等幾種常見的函數。對上述3種函數的比較顯示，雖然都能擬合出原曲線，但是相對而言，高斯函數的擬合精度更高，因此在本次研究中擬采用高斯函數構建基于ANFIS的水質預測模型。

在隸屬度函數確定之后，確定隸屬度函數的數目。根據相關研究成果和實踐經驗[6]，隸屬度函數的數目通常選取在[1，30]之間，研究中將不同數目的隸屬度函數依次帶入模型，實踐結果顯示，隸屬度函數的數目選定為5～20條之間時，ANFIS的水質預測模型均能對原曲線進行準確擬合，而隸屬度函數的數目少于3條的情況下，模型就不能對原曲線進行準確擬合。另一方面，函數數目的增加，雖然能夠提高擬合度的精準度，但是提高較為有限，模糊子集之間的相互影響會顯著降低模型的靈敏度。本次研究最終確定隸屬度函數的數目為5條。

2.3 模型訓練次數選取

針對訓練次數，根據相關研究成果，引入一個性能指標σ，設模擬精度為ε訓練次數為n，trRMSE(n)為訓練n次之后得到了RMSE值，根據公式(2)，當σ≤ε時的n的值極為最優訓練次數[7]。

σ=|trRMSE(n)-trRMSE(1)|

(2)

在本次研究中，初步設定模型的訓練次數為500次，結合上述設定的高斯函數以及函數數目為5條等相關參數，對模型展開訓練，獲得的RMSE隨訓練次數變化的曲線如圖2所示。由圖2可知，當訓練次數達到35次時，RMSE值的變化逐漸趨向平穩，根據公式(2)的要求，設定本次訓練精度為0.02，最終得到最優訓練次數為378次。

圖2 RMSE值訓練變化曲線

3 模型應用和檢驗

3.1 數據選擇

為了檢驗基于ANFIS水質預測模型的泛化性和實用性，研究中以遼寧省大伙房水庫出庫口的監測數據為研究對象，由于該站每隔6小時采集記錄一次水質監測數據，采集間隔時間合理，可以全面反映渾河該區段的水質情況。實驗選取的是大伙房水庫出庫口2017年4—10月的數據，其中4—9月的數據進行模型訓練，10月份的數據輸入模型進行測試，并將期望值和實際值進行對比分析。其中，2017年4月1日6時至2017年4月5日0時的各項水質指標數值見表1。

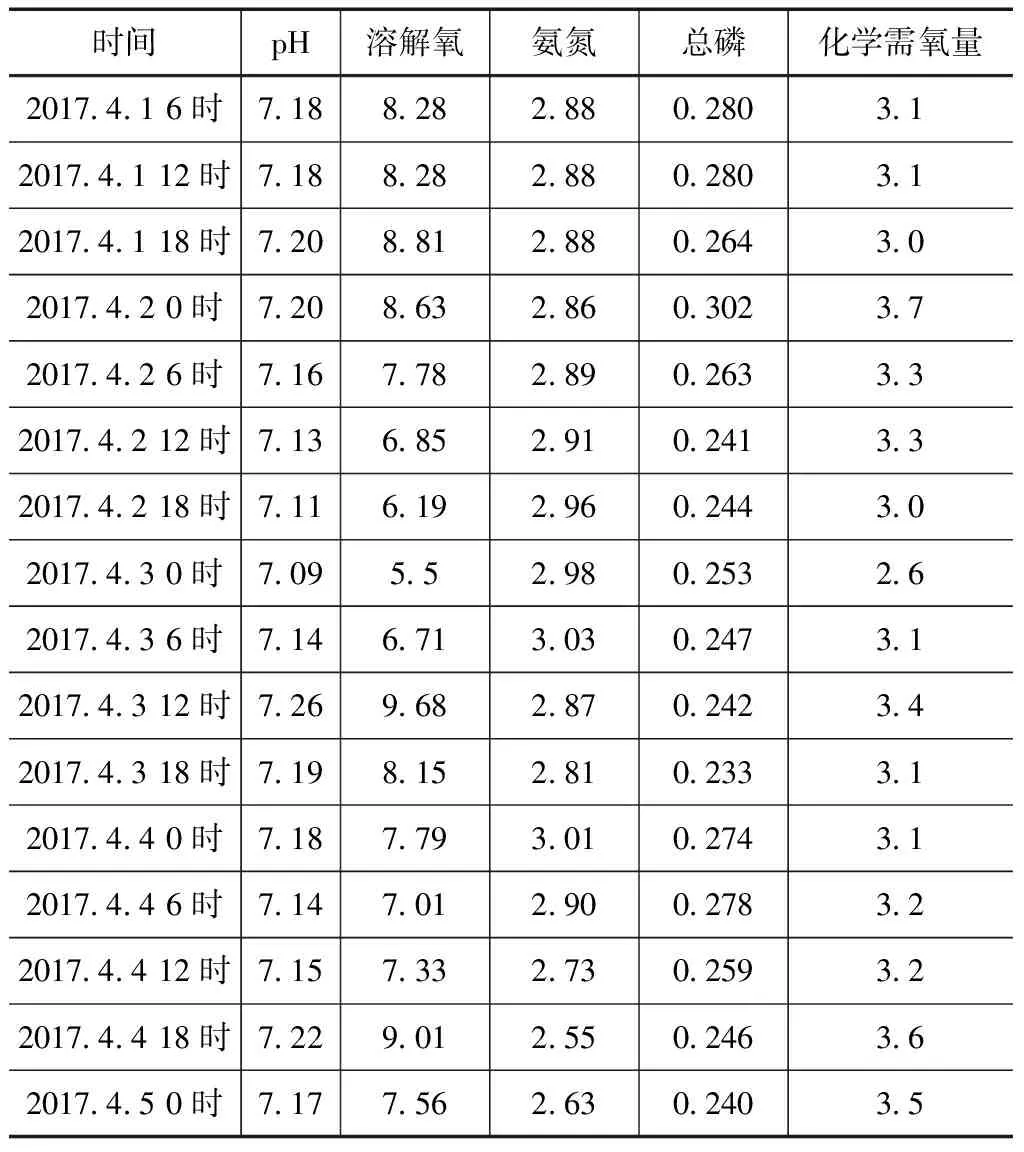
表1 大伙房水庫庫口水質監測部分原始數據單位：mg/L

3.2 預測結果分析

將原始數據進行預處理后，進行訓練樣本和測試樣本劃分，然后將訓練樣本輸入ANFIS模型進行訓練，在訓練完畢后將測試樣本輸入模型，計算得出COD值的預測結果，然后與實際值進行比較，結果如圖3所示。在軟件窗口顯示的模型預測值和實際值之間的相對誤差為0.0966，均方根誤差值為0.0610，均方根誤差為0.2363。由此可見，ANFIS模型的預測值與真實值之間具有良好的擬合性，說明模型本身具有較好的預測能力和準確性。

圖3 模型計算得出預測值與實際值

3.3 預測能力對比分析

為進一步驗證ANFIS模型的實用性和泛化性，橫向對比模型預測能力的優劣，研究中基于同組數據，分別利用BP神經網絡模型和RBF神經網絡模型進行預測計算[8]，其預測性能參數的對比結果見表2。由表2中的數據可以看出，ANFIS模型能夠對渾河大伙房水庫段水體中的COD含量進行較好的預測，從相對誤差來看，該模型的誤差為0.0966，顯著小于BP神經網絡模型的0.1315和RBF神經網絡模型的0.1485的相對誤差值。因此，ANFIS模型相較于BP神經網絡模型和RBF神經網絡模型具有更好的泛化性和實用性。

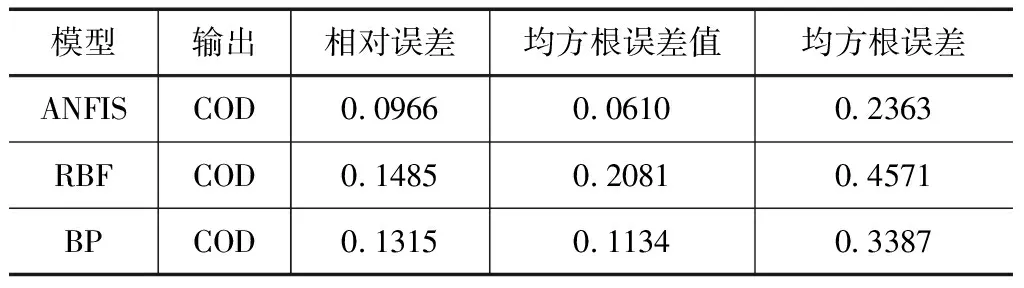
表2 不同預測模型的性能參數對比結果

4 結語

本文以渾河大伙房水庫庫口地表水為檢測對象，建立ANFIS預測模型對該河段水體COD含量進行了預測研究，并獲得如下結論。

(1)結合國家環保部的相關標準以及水質監測的實際需求，研究中選取COD、pH、溶解氧、氨氮和總磷等五個水質質量監測指標，并將COD作為預測模型輸出計算的基本參數。

(2)利用ANFIS模型對COD值進行預測計算，并將結果與實際值進行比較，結果顯示模型預測值和實際值之間具有良好的擬合性，說明模型本身具有較好的預測能力和準確性。

(3)將ANFIS模型與BP神經網絡模型和RBF神經網絡模型進行對比分析，結果顯示ANFIS模型相較于BP神經網絡模型和RBF神經網絡模型具有更好的泛化性和實用性。