一道高考選擇題的解法探析
2019-03-27 06:01:54武增明
數理化解題研究 2019年7期
武增明
(云南省玉溪第一中學 653100)
2017年高考全國卷Ⅰ理科數學第11題為:設x,y,z為正數,且2x=3y=5z,則( ).
A.2x<3y<5zB.5z<2x<3y
C.3y<5z<2xD.3y<2x<5z
解法1 ∵x,y,z為正數,∴可設2x=3y=5z=k>1(lgk>0).
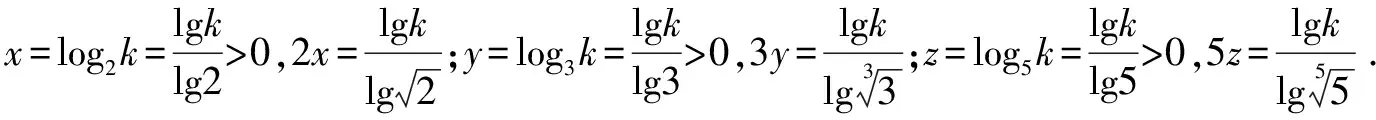
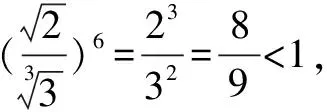
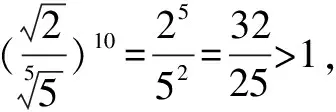
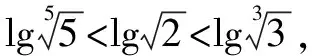
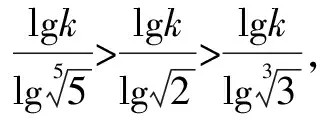
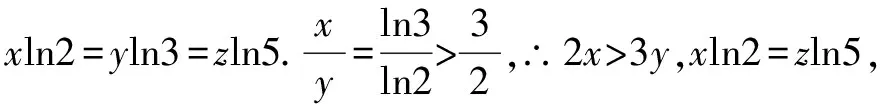

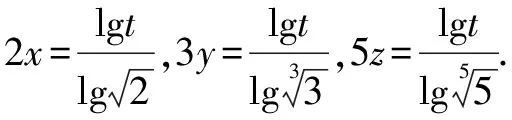
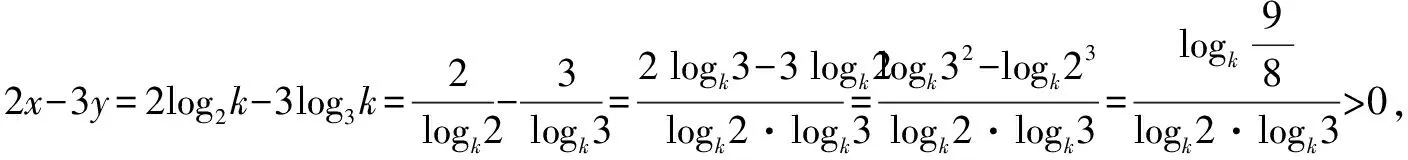
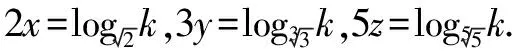
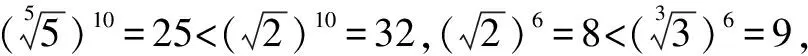
解法8 令2x=3y=5z=2,則x=1,y=log32,z=log52,此時,2x=2,3y=3log32=log38,5z=5log52=log532.易得2=log39>log38,log532>log525=2,所以5z>2x>3y.故選D.
認真反思一下,為何題目設計時底數選擇2,3,5,而不是3,4,6等等其它數字?帶著這種困惑,我們再從題目本身入手.
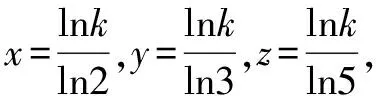
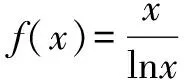
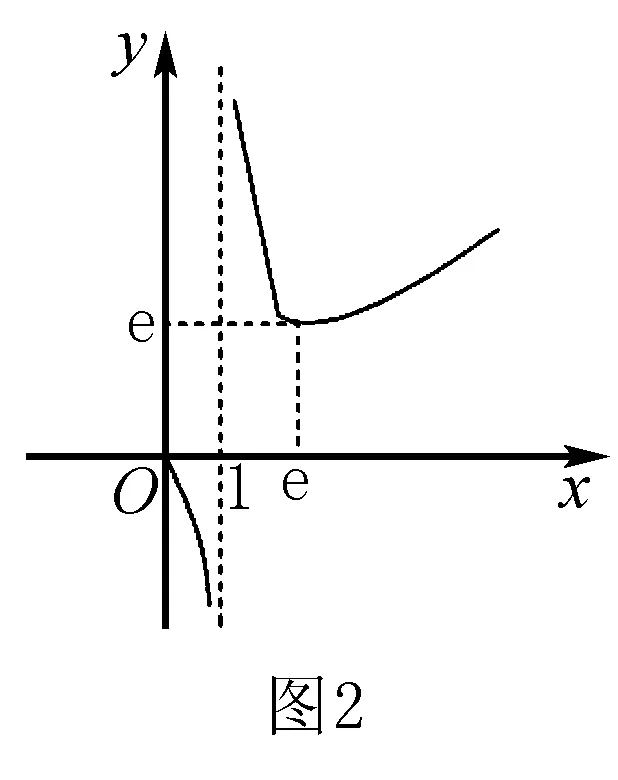
由此可見,原題中底數選用的2,3,5,它們都是e附近左右的整數值,相對應的數值接近且沒有秩序,有比較的價值,而3,4,6等其它數字卻都處于函數的單調區間且對應函數值有遞增趨勢,考生或許較便于做出選擇.所以,題目中底數的選用更適于對考生能力的考查.

