巧算負指數冪

◎朱 平

負指數冪的運算是冪的運算的一個難點，特別是遇到底數是分數時，運用書中所給公式計算不方便而且易錯。針對這種情況，我們進一步剖析負指數冪的運算公式并結合幾個具體實例來幫助同學們輕松解決它。

負指數冪運算法則：任何不等于0的數的-n次冪（n為正整數），等于這個數的n次冪的倒數。表達式為（a≠0，n為正整數）。由這個表達式可以進一步得到（a≠0，n為正整數）。因此，負指數冪的法則還可以是：任何不等于0的數的-n（n為正整數）次冪，等于這個數的倒數的n次冪。

例1 計算：（1）4-2；（2）-3-3。

運用另一個法則a-n=（）（na≠0，n為正整數）。

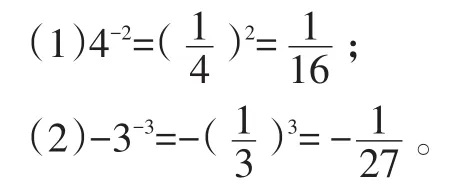
在這兩個題目的計算上，這兩種方法結果相同，難易相當。

運用另一個法則a-n=（）（na≠0，n為正整數）。

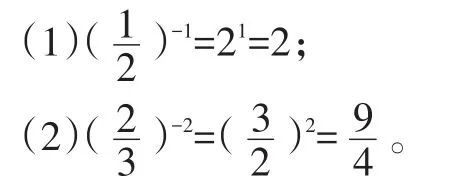
很明顯，遇到底數是分數的負指數冪運算時，采用我們新推導出的法則進行運算要方便很多。

【解析】此題求冪的乘除法混合運算，我們可以運用法則a-n=（）（na≠0，n為正整數）將（-）2變為（-2）-2，再按照同底數冪的乘除法法則進行計算即可。（-）2÷（-2）3×（-2）-2=（-2）-2÷（-2）3×（-2）-2=（-2）-2-3-2=（-2）-7=（-）7=-。這個題目還有另外一種做法，我們可以先將題目中的（-2）3變為（-）-3，（-2）-2變為（-）2，再按照同底數冪的乘除法法則進行計算。