基于余弦相似度的加權K近鄰室內定位算法
黃運穩 陳 光 葉建芳
(東華大學信息科學與技術學院 上海 201600)
0 引 言
隨著社會的進步與發展,人們對室內位置服務LBS(Location Based Services)的需求日益強烈[1]。將全球定位系統GPS應用于室內定位時,由于衛星信號受建筑物環境的影響很大,定位的效率較低,定位的精度也較差,因此不能達到實時和準確的定位要求。
隨著無線通信技術的應用發展,基于接收信號強度的Wi-Fi室內定位成為目前研究的熱點[2-3]。Wi-Fi信號不受視距傳播的影響,信號的覆蓋范圍較大,而且不易受到噪聲的干擾,適合于復雜的室內環境定位。尤其是,Wi-Fi指紋定位不用添加其他任何硬件,利用現有的WLAN,通過軟件編程就可以在移動智能終端上實現定位[4-6]。
有鑒于此,國內外學者近年來對Wi-Fi指紋定位的匹配算法做了大量深入的研究,其中KNN[7]、WKNN[8-10](K Weighted Nearest Neighbor)以及余弦相似度[11-12]算法由于計算簡單、易于實現而得到廣泛應用。以上算法的核心在于通過RSS進行歐氏距離或相似度的匹配。然而一方面,由于接收信號強度自身的不穩定性與環境的多變性,導致接收信號強度不能完全準確反映客觀物理位置。另一方面,歐氏距離體現的是接收信號強度數值的絕對差異,而余弦相似度是從方向上區分接收信號強度的差異,以上因素導致各算法在定位過程中容易引入奇異點[14]。針對上述問題,本文對K最近鄰和余弦相似度的組合策略進行了分析研究與實驗比較,給出了定位精度更高的優化組合算法。
1 Wi-Fi指紋定位匹配算法
1.1 KNN匹配算法
KNN算法通過測量兩個向量之間歐式距離來度量它們之間的相似度。該算法將待定位點采集到的信號強度RSS向量[s1,s2,…,sn]與指紋數據庫中的信號強度RSS均值矩陣[Si1,Si2,…,Sin]相匹配。設定位區域有m個參考點,共有n個AP,sj為待測點收到第j個AP的信號強度,Sij為指紋庫中第i個參考點采集到第j個AP的RSS均值,i=1,2,…,m,j=1,2,3,…,n。距離的定義公式如下:
(1)
KNN算法在歐氏距離中從小到大依次選取K個參考點,然后以該K個參考點的質心作為估計位置。
(2)
KNN定位算法原理相對簡單,以信號強度來反映物理位置關系,有利于定位系統的實現。
1.2 余弦相似度匹配算法
余弦相似度通過測量兩個向量內積空間夾角的余弦值來度量它們之間的相似性。余弦值越接近1,表示兩個向量的夾角越接近0度,向量的方向越相近,即表示兩個向量越相似。如A和B的余弦相似度的計算公式如下:
(3)
基于余弦相似度算法理論,定位點采集的RSS矩陣s=[s1,s2,…,sn]與指紋數據庫中第i個參考點的RSS均值矩陣Si=[Si1,Si2,…,Sin]相匹配,通過式(4)計算余弦值,以余弦值從大到小依次選取K個參考點,并以式(2)計算得出估計位置。
(4)
通過余弦相似度算法匹配,考慮了RSS向量的內在聯系。余弦相似度使用兩個向量夾角的余弦值作為衡量兩個向量間差異的大小。相比歐氏距離,余弦相似度更加注重兩個向量在方向上的差異。
2 基于余弦相似度的加權KNN算法
2.1 算法提出依據
針對以上對兩種定位算法的介紹,通過三維坐標來進一步分析歐式距離和余弦相似度的區別,如圖1所示。
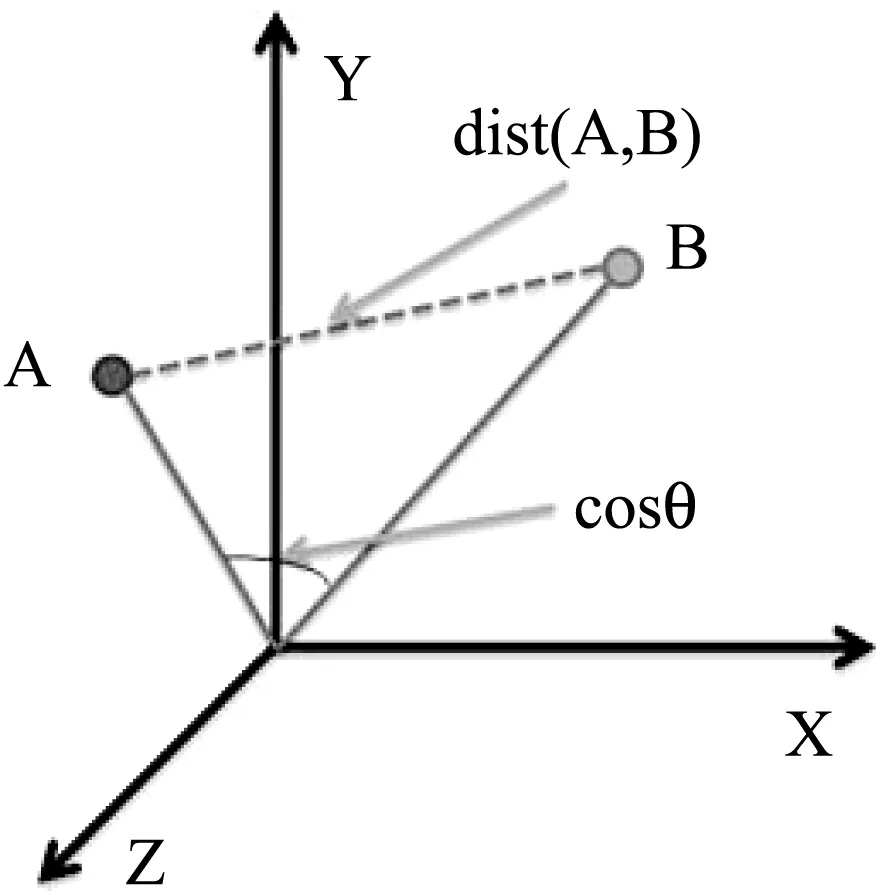
圖1 KNN與余弦相似度區別
由圖1可以看出,歐氏距離衡量的是空間各點的絕對距離,即與RSS向量各分量的大小直接相關;而余弦相似度衡量的是空間向量的夾角,體現的是RSS向量在方向上的差異。KNN和余弦相似度算法各自有不同的計算方式和衡量特征,KNN算法能夠體現RSS向量的絕對差異,余弦相似度是從方向上區分差異,而對絕對的數值不敏感。
針對以上分析,本文提出了基于KNN和余弦相似度的組合算法,旨在彌補單一區分方式的不足,從而提高定位精度。
2.2 算法步驟
在KNN算法篩選出K個近鄰點的條件下,計算K個近鄰點的余弦值。由1.2節分析可知,余弦值越大,表示兩個向量越相似,在歐氏距離相近的前提下,余弦值大的近鄰點定位精度越高。本文采用線下加權的方式來確定權值,從而包含位置指紋全部數據信息,進而提升定位精度。算法步驟如下:
1) 篩選近鄰點。基于式(1)計算出定位點RSS向量與指紋庫中各向量的歐氏距離Li,在Li中從小到大順次篩選出K個參考點,坐標為(xi,yi),i=1,2,…,K。
2) 計算余弦值。基于式(4)分別計算待定位點與K個參考點之間的余弦值,余弦值的大小分別為S1,S2,…,SK。
3) 確定權值。S1,S2,…,SK中,余弦值越大,在位置估算時所作的貢獻越大,那么第i個參考點的權重值ωi可表示為:
(5)
4) 位置估計。利用權重值對K個參考點估算定位點的位置坐標,即:
(6)
3 實驗分析
3.1 實驗環境與系統
為了檢驗組合算法的定位性能,進行如下實驗。實驗環境為東華大學2號學院樓第六層,平面圖如圖2所示。
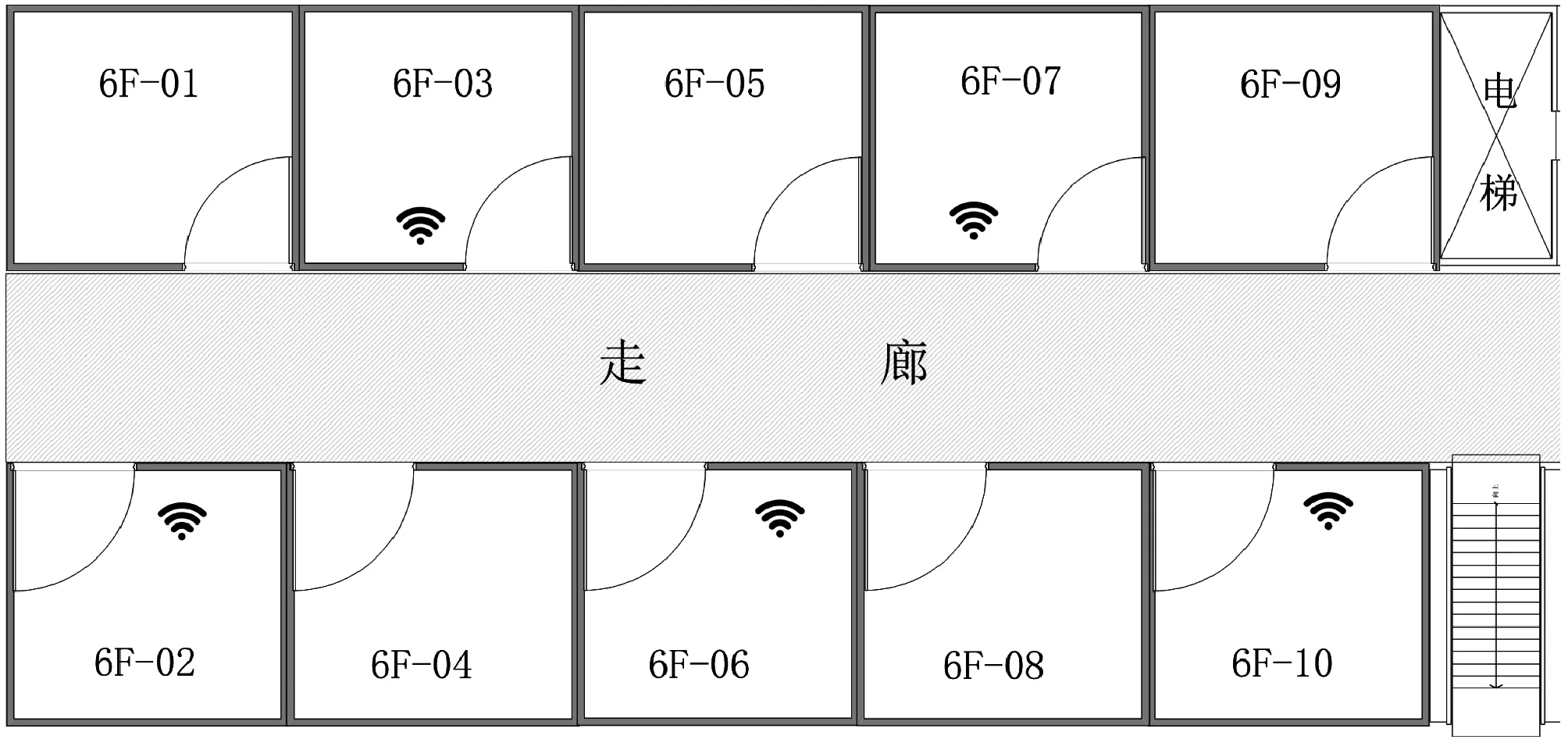
圖2 實驗環境平面圖
文獻[15]得出結論,當K=5或K=6時,系統定位的效果最佳。因此本文K值選擇5對參考點坐標進行篩選。其中數據庫信號采集與定位軟件界面如圖3所示。
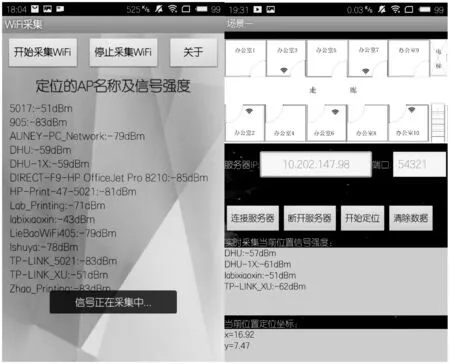
(a) 離線信號采集 (b) 在線定位圖3 軟件界面截圖
離線采集:選用魅族M578C建立離線指紋數據庫,并將數據庫信息存儲在服務器。離線采樣間隔為1 m,為了減少數據庫建立的誤差,每個離線采樣點采集20組數據,以20組信號強度均值作為采樣點的最終樣本值。其中,數據庫中的數據包括采樣點坐標、掃描到每個AP的ID和接收到每個AP信號強度。
在線定位:選取30個定位點測試,分別包括每個實驗室選取2個參考點,走廊選取10個參考點。移動終端向服務器發送連接請求,并向服務器發送當前RSS向量,服務器接受RSS向量后通過組合算法進行匹配,估算定位點的坐標,并將坐標信息發送到移動終端。
3.2 性能分析
圖4為走廊中間位置的定位點連續進行30次RSS采集,參與定位AP數量為5個時RSS的變化。由圖可知,室內環境復雜多變,引起AP信號強度起伏變化。因此單一的傳統算法極易造成匹配出現偏差,引入奇異點。
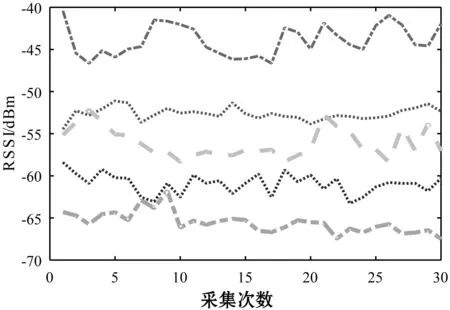
圖4 不同定位點信號強度變化曲線
首先在實驗環境中選2個AP參與在線定位階段,分別是6F-03和6F-07中的AP,采集30個參考點接收到參與定位的2個AP的數據,與數據庫中的數據相匹配,不參與定位的AP不匹配,計算此條件下,組合算法及傳統算法定位的平均誤差。然后每次增加一個AP參與定位,以相同方式算出不同算法的定位平均誤差。實驗中第六個AP是校園公共網絡。不同算法在AP個數不同情況下,定位平均誤差的結果如圖5所示。
圖5結果表明,當不同個數的AP參與定位時,組合算法的平均誤差均低于傳統算法,由此排除了組合算法在特定AP數量下提升定位性能的可能性。
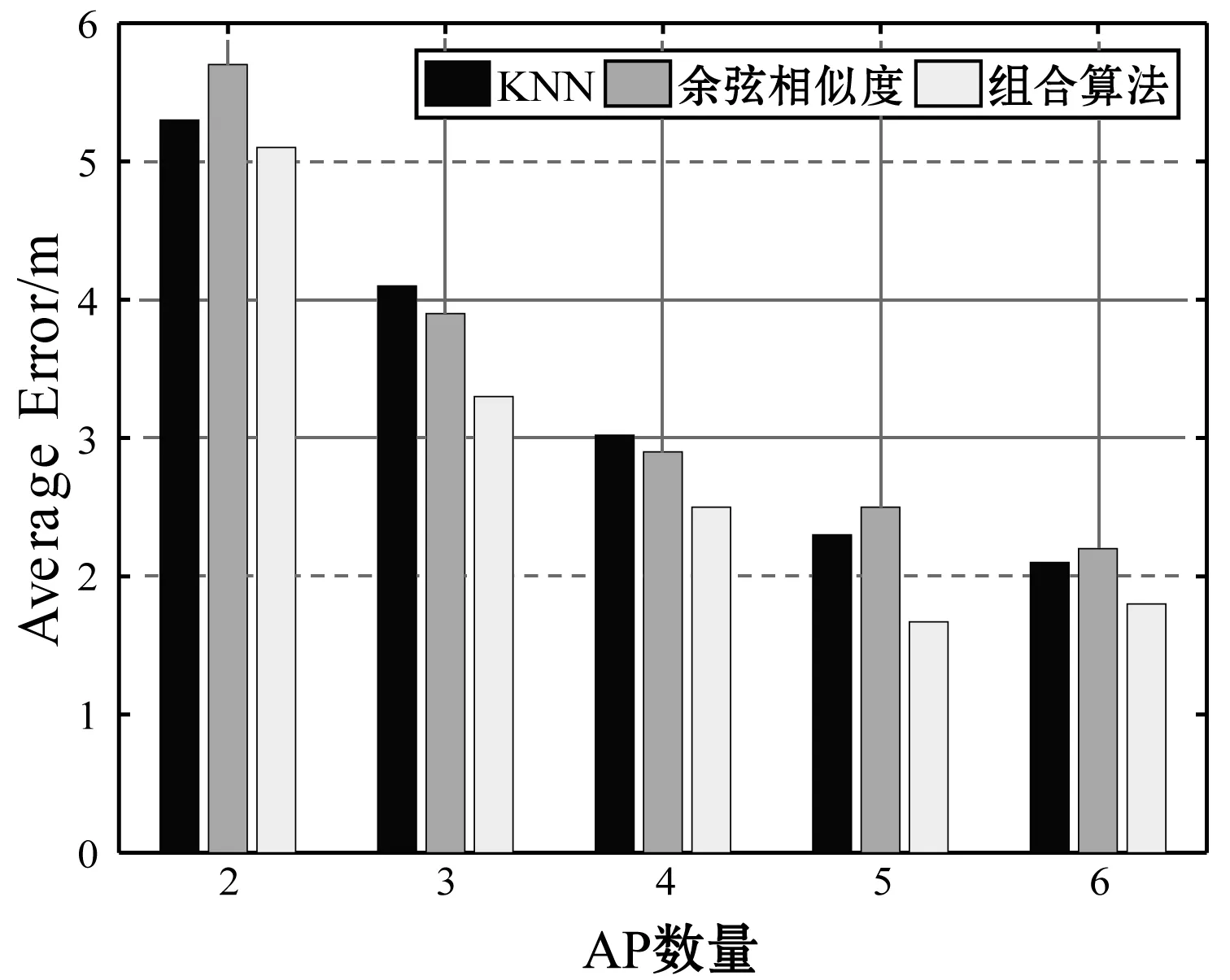
圖5 參與定位的AP個數對定位結果影響
根據性能分析中不同AP個數對定位精度影響,我們選用5個AP參與定位,進一步比較不同算法的累加誤差概率,如圖6所示。
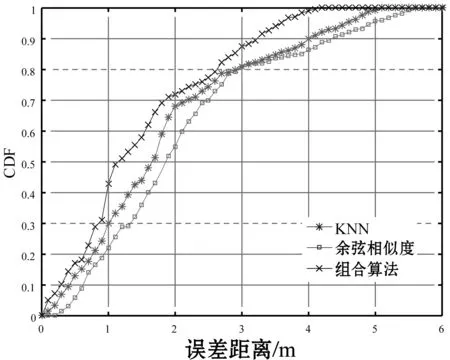
圖6 不同算法的CDF曲線
由圖6可知,本文提出的組合算法定位精度明顯優于單一的傳統算法。組合算法定位精度優于1 m的置信概率為42%,優于2 m的置信概率為72%,最大誤差為4.3 m,相對傳統算法均有改善。實驗結果表明,文中提出的基于余弦相似度的加權KNN算法能夠有效地提高室內定位的精度。
4 結 語
為了提高室內定位的精度,考慮到KNN和余弦相似度匹配算法在定位特點的互補性,提出了基于余弦相似度的加權KNN算法,從而彌補單一傳統算法的不足。實驗結果表明,基于余弦相似度的加權KNN算法在5個AP參與定位時,平均誤差減少到1.67 m,定位精度明顯提高。
隨著室內定位技術的發展,基于余弦相似度的加權KNN算法需要在更大面積的環境、更復雜的干擾因素、更大量的指紋樣本條件下進一步測試和優化,使得該算法更加完善。

