智能啟發算法在機器學習中的應用研究綜述

沈焱萍，鄭康鋒，伍淳華，楊義先

（1.北京郵電大學網絡空間安全學院，北京 100876；2.防災科技學院信息工程學院，河北 廊坊 065201）

1 引言

1952年，阿瑟薩繆爾開發了具有自學習能力的西洋跳棋程序，并首次提出“機器學習”概念。機器學習伴隨著人工智能的發展而發展，Mitchell[1]將其定義為“對于某類任務U和性能度量R，如果一個計算機程序在U上以R衡量的性能隨著經驗E而自我完善，那么我們稱這個計算機程序根據經驗E學習”。

根據解決問題所屬領域不同，機器學習可分為監督學習、無監督學習和強化學習[2]。在監督學習中，基于帶標簽的訓練數據建立訓練模型，常用方法包括人工神經網絡（ANN,artificial neural network）、支持向量機（SVM,support vector machine）、極限學習機（ELM,extreme learning machine）、K近鄰（KNN,K-nearest neighbor）和決策樹（DT,decision tree）等。在無監督學習中，根據不帶標簽的樣本數據建立模型，常用方法包括K-均值聚類（K-means）和自組織映射網絡（SOM,self organizing map）等。與監督學習、無監督學習不同，強化學習不知道在某一狀態下該做什么動作，而是不斷調整每一步策略，通過對學習過程獎勵的最大化實現策略最優，常用于路徑規劃、自動駕駛、棋盤游戲等場景。存儲技術的發展和大規模計算能力的提升使針對深度學習的研究受到較多關注，深度學習屬于機器學習的一個分支，它們與人工智能的關系如圖1所示[3]。

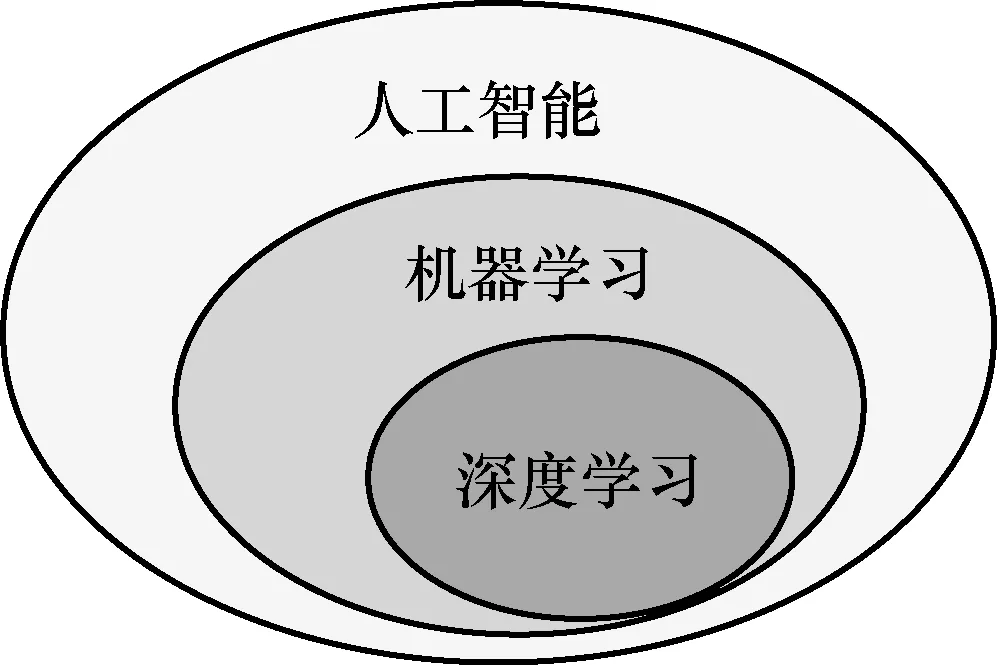
圖1 人工智能、機器學習與深度學習關系

建立理想機器學習模型面臨各種問題。例如，對于某些模型的構建，個別參數如神經網絡權重、核參數等的選取直接影響模型的準確率和泛化能力；諸多聚類算法的性能嚴格依賴于聚類中心的選取[4]，不僅影響算法的收斂性，對準確率也有很大影響；特征優化是構建機器學習模型的重要步驟，合適的特征集合既能節約系統資源又能準確表示原始數據；集成學習是機器學習領域的重要研究內容，如何選取合適的基學習器，如何將基學習器有效地組合起來是集成學習面臨的重要問題；KNN存在計算效率低、存儲需求大和易受噪聲影響等缺陷。采用數據約簡技術可同時解決上述問題。近年來，隨著SVM算法的發展和完善，核思想有效應用于非線性模式分析問題中。然而，不同的核函數性能不同，當遇到數據含有異構信息、數據分布不平坦等復雜情況時，單個核函數不能滿足實際需求，因此，研究多核學習方法成為當前熱點。

綜上可知，機器學習模型必須經過優化才能發揮理想效果。優化方法主要包括2類：數學優化方法和智能啟發算法。數學優化方法主要依靠目標函數的梯度信息進行尋優，還需要一個良好的起點保證算法成功收斂。對于計算代價高昂的搜索推導問題，基于數學的方法是無效的。常用的數學方法包括牛頓法、動態規劃法（DP,dynamic programming）等。近年來，智能啟發算法在工程應用中越來越受歡迎，因為它們具有依賴于相對簡單的概念并且易于實現、不需要梯度信息、可繞過局部最優、可用于涵蓋不同學科的廣泛問題等優勢[3]。智能啟發算法只通過輸入和輸出來考慮和解決優化問題。換句話說，智能啟發算法將優化問題假設為一個黑盒，因此不需要計算導數，這使其在解決各種各樣的問題時具有高度的靈活性。數學優化方法和智能啟發算法尋優過程對比如圖2所示。

對智能啟發算法的重要研究工作如下。密德薩斯大學（Middlesex University）的Yang等提出了蝙蝠算法（BA,bat algorithm）[5]、螢火蟲算法（FA,firefly algorithm）[6]等，同時對智能啟發算法的特征、數學證明及應用場景進行研究；格里菲斯大學（Griffith University）的Mirjalili等提出一系列新的智能啟發算法，包括蜻蜓算法（DA,dragonfly algorithm）[7]、鯨魚優化算法（WOA,whale optimization algorithm）[8]、灰狼優化（GWO,grey wolf optimizer）算法[9]、蟻獅優化（ALO,ant lion optimizer）算法[10]、樽海鞘群算法（SSA,salp swarm algorithm）[11]等，在算法設計的過程中注重探索和利用的平衡；亞伯大學（Aberystwyth University）的研究者采用啟發算法，尤其是和聲搜索算法（HS,harmony search）進行特征選擇、集成約簡等。

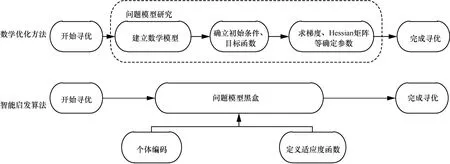
圖2 傳統優化方法和智能啟發算法尋優過程對比

Talbi[12]認為純啟發式算法一般不適用于高維度、復雜的應用場景，提出將數學規劃、約束規劃、機器學習算法與啟發式算法相結合從而改進啟發式算法，從算法設計和算法執行兩方面進行闡述,同時指出應根據特定的問題設計合適的混合方案。與Talbi的研究不同，本文提出如何將智能啟發算法應用于機器學習領域以提高機器學習算法的效率和精度。基于智能啟發算法的機器學習建模過程如圖3所示，將基于某些特征或樣本的訓練數據輸入核心機器學習算法中，在智能啟發算法的幫助下，分析和學習訓練集中的數據模式，得到訓練好的模型和樣本特征。模型的優化過程涉及模型的多次訓練，由智能啟發算法的迭代次數決定，應用智能啟發算法必須確保其收斂。最后，將測試數據輸入訓練好的算法模型中，得到最終輸出結果。

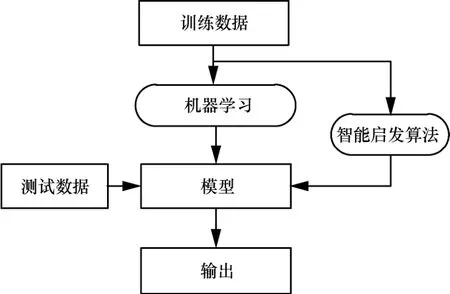
圖3 基于智能啟發算法的機器學習建模過程

2 智能啟發算法分類及建模

2.1 算法分類

智能啟發算法可分為2類：基于個體（single-solution-based）的方法和基于種群的（population-based）方法。基于個體的方法指搜索過程從一個候選解開始，在隨后的迭代過程中不斷改進這個單一候選解，典型算法有爬山法[13]、模擬退火（SA,simulated annealing）算法[14]、禁忌搜索（TS,tabu search）算法[15-16]等。基于種群的方法采用一組解來執行優化，搜索過程從隨機初始種群開始，并且種群在迭代過程中得到改進。基于種群方法的搜索過程分為兩步：探索階段和利用階段。探索階段指盡可能廣泛地探尋搜索空間中有前途區域的過程；利用階段指在探索階段獲得的有前景區域周邊的本地搜索。與基于個體方法相比，基于種群方法中個體相互協助、共享搜索空間信息，避免陷入局部極值，具有更大的探索性。典型算法有粒子群優化（PSO,particle swarm optimization）算法[17]、遺傳算法（GA,genetic algorithm）[18]等。

智能啟發算法具體分類如圖4所示，包括進化算法、基于物理規則方法、群智能算法和基于人類行為的方法[7]。進化計算模擬自然界生物進化過程，采用“優勝劣汰”達到進化目的，典型算法包括遺傳算法、進化策略（ES,evolution strategy）[19]、基因編碼（GP,gene coding）[20]和差分進化（DE,differential evolution）算法[21]等。基于物理規則（physics-based）的方法指通過模擬自然界中的物理現象概括出的啟發式算法。一組代理通過某種物理規律，如重力、運動定律、光線投射、電磁力、慣性力等在搜索空間中移動，并根據一定規律相互通信。典型算法有引力搜索算法（GSA,gravitational search algorithm）[22]、收費系統搜索算法（CSS，charged system search）[23]、中心力優化（CFO,central force optimization）算法[24]和大爆炸（BBBC,big-bang big-crunch）算法[25]等。群智能（SI,swarm intelligence）算法從鳥類、螞蟻等動物行為中獲得靈感，具有通過個體間交互解決復雜任務的能力，典型算法包括粒子群優化算法、蟻群優化（ACO,ant colony optimization）算法[26]、蜂群（ABC,artificial bee colony）算法[27]和布谷鳥搜索（CS,cuckoo search）算法[28]等。群智能算法和進化算法在種群迭代方式上不盡相同，群智能算法側重群體中個體之間的協作，而進化算法側重個體的進化。還有一些受人類行為啟發（human-based）的智能搜索方法，如教與學優化（TLBO,teaching learning based optimization）算法[29]、和聲搜索[30]、禁忌搜索和組搜索優化（GSO,group search optimizer）[31]等。

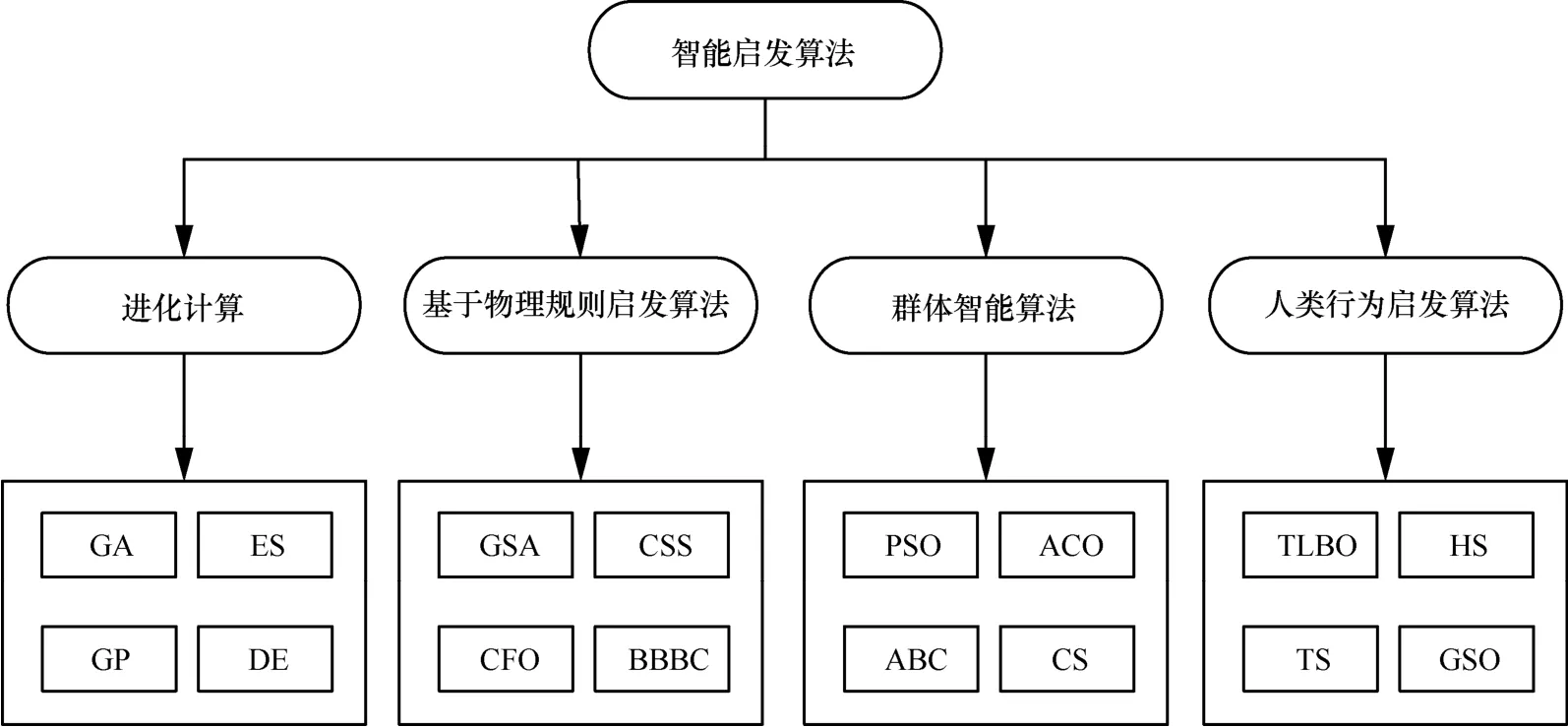
圖4 智能啟發算法分類

值得一提的是，無免費午餐（NFL,no free lunch）定理[32]在邏輯上證明了單一智能啟發式算法不能解決所有優化問題。換句話說，一個特定的智能啟發方法可能在一組問題上顯示出較好的性能，但在另外一組問題上可能表現出較差的性能。因此，當前智能啟發算法需要不斷被改進，也需要提出新的智能啟發算法。

2.2 算法建模

2.2.1 個體編碼

采用智能啟發算法首先需要考慮個體編碼問題，這將直接影響算法搜索的精度和效率。

有效的編碼方式能在保證算法執行效率的前提下簡單明了地表示問題的解，并支持后續算子的各種操作變化。常用編碼方式優缺點及應用場景如表1所示。智能啟發算法大多采用矢量方式編碼，包括數值編碼和符號編碼。數值編碼即根據實際需求或算法特點采用二進制或實數方式編碼。經典遺傳算法本身采用二進制編碼，大多數智能啟發算法基于實數編碼被創建。智能啟發算法還可采用符號編碼，有時要求的解僅僅是一種類型信息，并不具有任何數值意義，可采用特殊意義的符號組合表示此類問題的解。

目前的啟發算法能解決相關參數確定和類型選擇問題，但無法解決多類型組合及嵌套問題，基于非線性結構編碼的啟發算法應運而生。例如，對于遺傳算法、遺傳規劃（GP,genetic programming）[33]，個體可采用樹形結構、堆棧結構等編碼方式解決此類問題。

個體編碼長度由實際問題維度或精度決定，一般來說個體表達不能太長，否則不僅影響算法搜索效率，還會使算法尋優性能下降[34]。不管采用何種編碼方式，都在迭代結束前對產生的新個體進行評估。

2.2.2 適應度函數定義

適應度函數的定義對于智能啟發算法建模至關重要，直接決定了收斂結果。適應度函數用于評估個體在迭代過程中的優劣，指引算法向何處搜索，通常根據實際問題的需求進行定義，例如對于分類問題，準確率、錯誤率、召回率、F值可作為適應度函數評估標準；對于回歸問題，可以定義均方誤差作為適應度函數。本節以用于分類的監督學習算法為基礎，如快速學習網絡（FLN,fast learning network）[35]等介紹啟發算法進行優化時幾種常見的適應度函數，其定義如表2所示。表2中，w1和w2分別表示不同評估度量的權重，必須保證不同評估度量的取值范圍是一致的。采用此種方式定義的適應度函數應事先確定搜索目標的極大值或是極小值，例如對于入侵檢測問題，在進行特征選擇的同時提高檢測性能，為了獲得最佳適應度值，個體必須最大化檢測率、最小化虛警率和特征個數。為了達到最佳適應值，檢測率的權值應設置較高，虛警率和表示特征個數的權重應設置相對較小，因為檢測率是相對重要的目標度量。

表1 編碼方式優缺點及應用場景

還可根據實際需求定義帶約束條件或多目標優化的適應度函數。采用罰函數等方法將約束優化問題轉化為無約束優化問題。如果涉及多種度量，可通過表2所示的加權適應度函數將多目標優化轉變為單目標優化問題。此外，還可定義多目標適應度函數，目前已經提出多種實現多目標優化的方法[7]。智能啟發算法試圖盡可能精確地找到一組稱為帕累托最優集的解。

對于具體問題，將其看作一種優化搜索問題，研究其評估標準，采用智能啟發算法定義合適的目標函數進行搜索，可起到事半功倍的效果。智能啟發算法建模流程如下。

1)設置算法相關參數，例如迭代次數、種群規模等。

2)按照個體編碼規則初始化種群。

3)根據適應度函數找出初始種群最佳個體。

4)按照個體變異規則產生新一代種群。

5)根據適應度函數計算新一代種群最佳個體。

6)重復步驟4)和步驟5)，直到迭代次數終止或滿足最佳適應度值。

7)輸出最優解。

2.2.3 復雜度分析

智能啟發算法屬于黑盒優化算法，不同啟發算法的迭代有其自身固定的操作環節。例如，對于PSO算法，個體需要通過速度更新式計算粒子新的速度，根據速度求出粒子的最終位置；對于差分進化算法，個體位置更新需經歷變異、交叉和選擇等過程。由分析可知，同一類別不同啟發算法迭代規則雖不盡相同，但由此產生的復雜度差別并不大。算法復雜度主要由適應度函數決定，對每一代種群中的每個個體都需計算適應度值，假設其復雜度為O(fitness)，則基于啟發算法優化模型的算法復雜度為O(fitness)×sizepop×NoIter，其中，sizepop為種群規模，NoIter為迭代次數。

3 智能啟發算法在機器學習中的應用

建立理想機器學習模型面臨各種問題，例如，對于多核學習任務，傳統的多核學習方法通常將問題表述為核函數和分類器的最佳組合的優化任務，通常是一些很難解決的具有挑戰性的優化任務[36]；而采用智能啟發算法對機器學習算法模型進行優化，可以避免將問題復雜化，從側面以仿生學的方式解決問題。基于智能啟發算法的機器學習模型優化體系如圖5所示，包括神經網絡等參數結構優化、特征優化、集成約簡、原型優化、加權投票集成、核函數學習等。

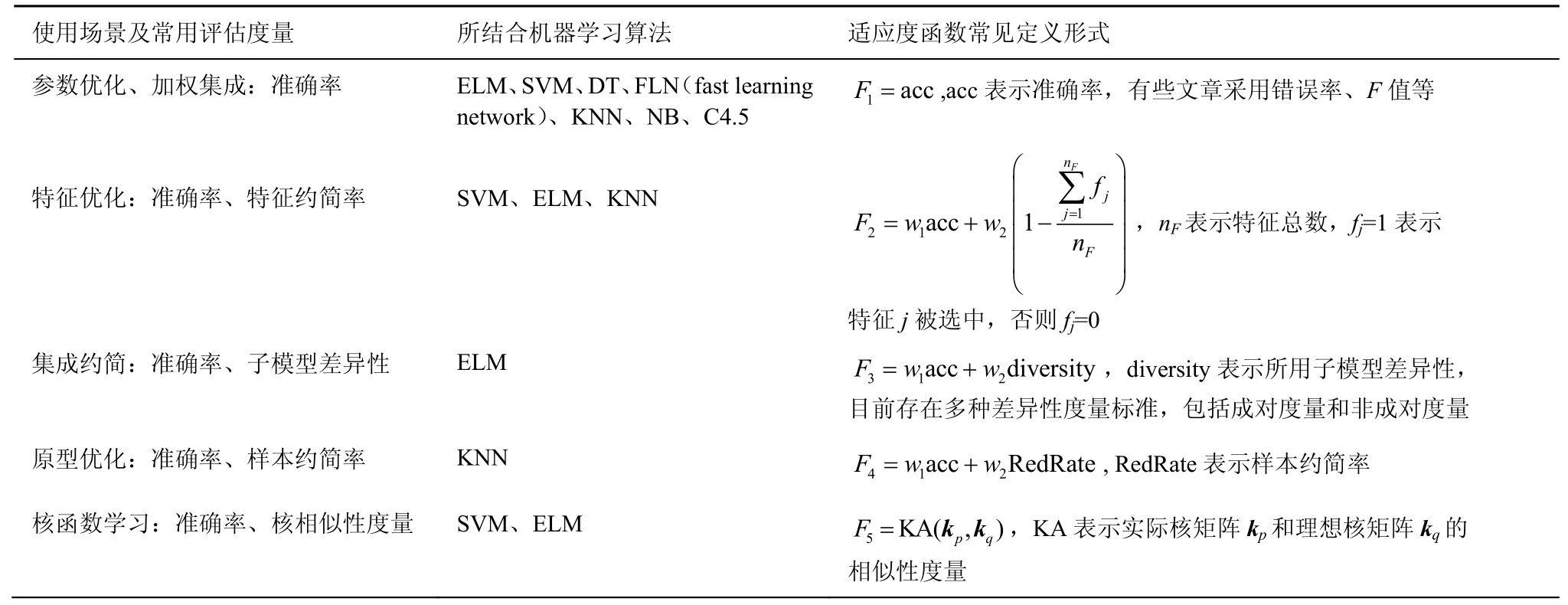
表2 智能啟發算法常用評估度量及適應度函數定義形式

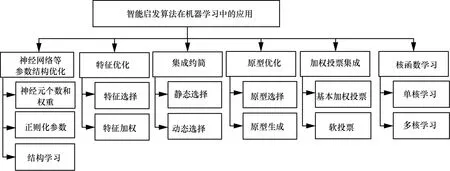
圖5 基于智能啟發算法的機器學習模型優化體系

3.1 神經網絡等參數結構優化

基于神經網絡等機器學習算法建立的模型必須經過調參才能發揮理想效果，深度學習方法也是如此。由于任何一個網絡模型都無法適用于所有數據集，因此，將深度學習方法應用于新數據集之前，必須先選擇一組適當的超參數[37]。對于卷積神經網絡（CNN,convolutional neural network），這些超參數包括網絡層數、每層隱藏節點數、層的激活函數、網絡中層的排列等。為一組新的數據集選擇新的網絡拓撲可能是一項耗時的任務。

在ELM中，隨機選擇輸入權重，并通過分析計算輸出權重。由于輸入權重和隱藏偏差確定的隨機性，ELM可能需要更多的隱藏神經元。Ahila等[38]提出了一種混合優化機制，將離散值粒子群算法與連續值粒子群算法相結合，對輸入特征子集選擇和隱藏節點數進行優化，以提高ELM的性能。Zhu等[39]采用差分進化算法確定ELM輸入和輸出權重。Zhang等[40]提出一種新的memetic算法優化ELM相關參數，將局部搜索策略嵌入全局優化框架中以獲得最優的網絡參數。Camilleri等[41]采用網格搜索和一種簡單遺傳算法優化決策樹ID3相關參數，包括單點最小增益、樹的最大深度和最小分割標準。Kardan等[42]提出一種基于生物地理學優化（BBO,biogeography based optimization）算法的改進K近鄰的混合算法。BBO同時對特征選擇、特征權重和鄰域大小進行優化。Costa等[43]提出一種基于最優路徑森林算法（OPFC,optimum-path forest algorithm）的入侵檢測模型，采用智能啟發方法估計概率密度函數，所用智能啟發方法包括蝙蝠算法、螢火蟲算法、引力搜索算法、和聲搜索方法和粒子群優化算法。實驗結果表明，所有智能啟發方法都比窮盡搜索方法快，但BA和PSO在效率和有效性方面都取得了最好的效果。結構學習是貝葉斯網絡（BN,bayesian network）研究領域的一個重要問題。為找到一個基于訓練樣本的最優結構，人們提出許多方法，Gheisari等[44]提出一種基于粒子群優化的BN結構學習算法。支持向量機是近些年應用較廣泛的機器學習算法，為了構造一個精確的支持向量機分類器，必須確定核函數、核參數和軟邊界常數（也稱為正則化參數）。對于參數的選取，智能啟發算法的應用提供了一些思路。目前，有大量關于SVM相關參數的優化方案[45-46]。智能啟發算法優化參數如表3所示。

隨著計算機技術的發展，神經網絡、進化算法等智能計算方法已經取得了巨大的進步，它們都是將生物學原理應用于科學研究的理論成果。二者可以相互補充、彼此強化，從而獲得更強大的表現和解決實際問題的能力[47]，它們的融合產生一種新的神經網絡稱為進化神經網絡。進化網絡通常是前饋網絡，需要研究其他類型網絡的進化算法，目前的研究大多是基于特殊情況，尚未形成通用的方法論，需要與粒子群等其他優化算法進行比較，而且計算復雜，需要改進演化過程，特別是研究并行進化算法的應用。

表3 智能啟發算法優化參數

3.2 特征優化

降維是建立有效機器學習模型的關鍵步驟。通常來說，降維方法有以下2種：特征選擇和特征提取。特征選擇可去除不相關或冗余特征，在進行分類時獲得比原樣本集相當或更好的效果。特征提取試圖通過組合原始特征來降低維數，這種方法試圖將信息損失降到最低，但是通常會丟失原始特征。

特征加權可以看作特征選擇的泛化[48]。假設原始特征為F={f1,f2,…,fH}。特征加權算法試圖為每個特征f∈F分配一個通常在[0,1]的權重wf，權重反映了特征f針對特定問題的相關程度。特征選擇算法每個特征的權重為wf∈{0，1}，wf=1 時特征f被選中，否則被丟棄。相比特征選擇硬性地選擇一部分特征，特征加權是一種特征選擇軟方案。有些特征選擇算法是根據特征權重的大小選擇合適的特征子集，特征權重較小的被移除。這里的特征優化指特征選擇和特征加權。

常用的特征選擇方法包括過濾法（filter）和封裝法（wrapper）。過濾法與后續算法無關，根據原始數據集的統計性能選擇特征。常用的過濾法包括[49]：基于距離的方法，如relief等；基于信息度量的方法，如信息增益（IG,information gain）；基于依賴性度量的方法；基于一致性度量的方法。封裝法與后續學習算法相結合進行特征選擇，例如根據后續學習算法的準確率選擇合適的特征。常用封裝法包括完全搜索法、啟發式搜索法、隨機搜索法等。封裝法以后續學習算法為指引開展工作，通常比過濾法有更好的學習效果。基于智能啟發算法進行特征選擇（特征加權）大多屬于封裝法。

貪婪搜索和relief等特征優化方法要么易陷入局部最優，要么只進行特征排序，并不考慮特征交互。而進化計算技術具有很強的全局尋優能力，在進行特征選擇問題上顯示出了比其他方法更大的優勢。Kashef等[50]提出采用改進二進制ACO進行特征選擇，特征被視為圖中的點，要求螞蟻必須訪問所有特征，采用幾種統計度量作為啟發式函數檢查圖中邊緣的可見性。Zelenkov等[51]采用遺傳算法進行特征選擇，選用準確率作為適應度函數。Diao等[52]對應用于特征選擇的10種不同啟發算法進行比較，結果表明所有算法都可以找到質量較優的特征子集，其中模擬退火算法和禁忌搜索算法可以達到更好的評估適應度值。Mateos等[53]提出一種基于進化計算的KNN改進規則，統一2個經典加權范式，即對每個鄰居的貢獻度和數據特征的重要性同時進行調整，以更好地識別新的實例。文本自動聚類已成為一種有效的文本分析方法，Bharti等[54]在聚類前采用二進制粒子群優化算法進行特征選擇，采用添加變異取反策略改進二進制粒子群算法增強搜索性能。Li等[55]采用改進灰狼算法進行特征選擇，采用GA確定灰狼初始種群位置。Zhang[56]借用SA、混沌相關思想改進FA增強全局搜索能力，并將其應用于分類和回歸模型中進行特征選擇。

如果要選擇的特征數量是固定的，可以選用十進制編碼；如果要選擇的特征數量事先沒有確定，則采用常規的二進制編碼。值得一提的是，在確定基學習器相關參數時，可采用特征選擇算法在進行特征選擇的同時對支持向量機的正則化參數、核參數進行優化，因為特征子集的選擇對適當的內核參數有影響，反之亦然。

大量實驗表明，基于智能啟發算法的特征優化方法通常與基于filter的度量方法結果保持一致。不同的啟發算法能否識別出不同的特征子集，從而采用特征選擇集成構造出更高質量的特征子集是值得進一步研究的。實驗結果還表明，每種啟發算法在處理不同的數據集時可能有其自身的優勢和弱點，可以開發一種元框架，動態地識別合適的算法，以形成一種更智能的、混合的特征優化方法。

3.3 集成約簡

多分類器集成系統（MCS,multiple classifier systems）的構建由三部分組成：子模型產生、子模型選擇及子模型的集成方式[57]。集成約簡（ensemble pruning）又稱集成選擇（ensemble selection），是子模型創建和子模型集成的中間環節，集成約簡的主要工作是減少將要集成的子學習器的數目。假設分類器池為C={c1,c2,…,cM}，M為所有分類器的數量。集成約簡的目的是尋找一組分類器C'?C，使基于C'在測試集上的性能類似或優于基于C在測試集上的性能。減少子學習器數量可以消除部分運行開銷，使集成處理更快，同時也意味著較小的內存和存儲需求；刪除冗余成員也可改善集成系統子學習器的多樣性，進一步提高系統預測精度。目前常用的集成約簡算法包括基于某度量的子模型排序方案、基于聚類的集成約簡方案和基于優化算法的約簡算法等。Cruz指出集成選擇分為靜態選擇和動態選擇，在靜態選擇中，選用固定的子模型子集對測試樣本進行預測；而動態選擇對于不同的測試樣本選用的子模型子集不同。目前存在的大部分集成約簡技術都屬于靜態選擇。

集成約簡和特征選擇思想類似，都是采用某種方法選擇原始集合的子集，Zhou等[58]提出一種基于GA的集成約簡模型，給每個神經網絡即子分類器賦予一個權重，該權重表示將該神經網絡包含在集成中的可能性，將權重大于預設閾值的子模型加入集成中。實驗結果表明，使用一定數目的子學習器比使用所有的子學習器效果更好。Diao等[59]將集成學習預測比作訓練樣本，將分類器視為特征，將特征選擇相關思想應用在分類器集成約簡，采用全局啟發式和聲搜索算法進行集成約簡。Shen等[60]采用二進制蝙蝠算法對投票極限學習機集成算法進行約簡，并應用于入侵檢測領域，驗證了Zhou提出的“many could be better than all”相關思想。Krawczyk等[61]也將集成約簡問題看作搜索問題，提出一種基于螢火蟲算法的one-class分類器集成約簡框架，基于聚類的集成修剪思想，發現類似的分類器組，并用一個相關的代表來代替它們，最后將選出的分類器進行權重組合。Hu等[62]提出一種分布式入侵檢測框架，采用在線AdaBoost算法在每個節點上構造局部檢測模型，采用PSO挑選合適的局部模型進行整合，最終采用支持向量機進行全局檢測。

一般的集成約簡策略都是通用的，屬于框架方案適用于任何子模型。在未來的工作中，針對不同的應用場景選擇相適應的子模型，并選用適當的評估標準，如準確率、差異性度量等多目標適應度評估標準，生成適合的集成約簡方案需要進一步考慮。如何擴展并改進現有約簡算法以解決機器學習中存在的概念漂移、超參數選擇等問題也需要進一步考慮[63]。

3.4 原型優化

原型優化用來實現數據約簡或原型簡化。由于近鄰（NN,nearest neighbor）模型存在存儲需求大、易受噪聲影響等問題，常采用NN模型指引數據約簡。假設樣本表示為(xi,yi)，其中xi=(xi1,xi2,…,xiD)∈RH，H為特征總數，yi表示樣本標簽，NN模型一般采用歐氏距離評估樣本相似度，如式(1)所示。

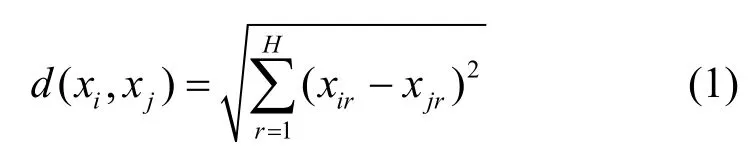
其中，d(xi,xj)表示樣本xi和xj的歐氏距離，xir表示樣本i的第r個特征。

假設P表示一組原始數據，原型優化的目的是從原始數據P中尋找一組約簡子集P'使|P'|<<|P|，約簡子集P'可能包含和原始數據P中相同的樣本，也可能包含根據原始樣本組成的新樣本。原型優化指從原始數據集生成一組原型，使基于生成數據訓練的近鄰模型可以接近（或優于）基于原始數據生成的學習模型。原型優化可分為原型選擇（PS,prototype selection）和原型生成（PG,prototype generation）技術。PS技術用來識別原始數據集的最佳子集，PG關注創建一組可以表示原始數據的新對象。與特征選擇相同，PS和PG技術也可以分為filter和wrapper這2種[64-65]。常見的PS算法包括剪輯近鄰法（ENN,edited nearest neighbor）[66]與壓縮近鄰法（CNN,condensed nearest neighbour）[67]。傳統的PG方法包括學習矢量量化[68]、bootstrap技術[69]和高斯混合方法[70]。進化計算是一種新的原型生成方法。

Nanni等[71]提出一種基于PSO的原型約簡方法。算法流程類似于對隨機森林中隨機子空間的處理。在訓練階段，重復生成原型多次，然后使用每個訓練模型對每個測試樣本進行分類，最后通過多數投票規則將分類結果組合起來。Hu等[72]提出一種PSO多目標優化原型生成方法。Triguero等[73]介紹了一種位置調整的原型生成方法，采用差分進化方法對原型進行定位優化。Rezaei等[74]采用重力搜索算法生成原型，利用分層策略提取初始對象。實驗表明，基于GSA的原型生成技術可以提高KNN分類器的性能。

Perez等[75]采用混合差分進化算法和CHC遺傳算法同時進行特征選擇、實例選擇、特征權重和實例權重調整。Derrac[76]采用一種協同進化算法同時優化樣本和特征權重并進行原形選擇。Escalante等[77]介紹一種基于遺傳規劃的原型生成技術，所提方法將多個訓練樣本通過算術運算結合起來生成目標原型，采用1NN作為評估分類器。Verbiest等[78]提出一種原型選擇框架，將多個最佳原型子集進行集成，給出4種最先進的基于進化的PS方法，包括世代遺傳算法（GGA，generational genetic algorithm）、穩態遺傳算法（SSGA，steady state genetic algorithm）、穩態memetic算法、擴展GGA的自適應實例選擇搜索算法。GGA和SSGA都遵循進化算法一般方案，不同之處在于SSGA在每代中只生成2個新的個體，而GGA則取代一部分個體；穩態memetic算法即在SSGA算法中添加優化策略。4種基于進化算法進行原型選擇的適應度函數定義如表2中F4所示。

為了增加算法在海量數據上的執行效率，應著重于研究進化算法的分布式，如MapReduce的編程模型。了解每種原型優化方法的主要優點，根據所解決的問題選擇合適的原型優化方法也是需要進一步考慮的問題。

3.5 加權投票集成

對3.3節中提到的集成學習的第三個步驟子模型的集成方式，即子模型的組合策略，使用最多的是多數投票和加權投票組合策略。多數投票根據投票最多作為最終預測結果，由于概念簡單、直觀、有效而被廣泛使用。然而不同的子學習器發揮的作用不同，因此可采用加權投票的方式進行組合。

根據分類器的輸出（標簽類別或概率類別），加權投票集成可分為基本加權投票和軟投票系統[72]。假設分類標簽yn為yn∈{ω1,…,ωD}，其中，ωj表示類別j，D為類別總數。C={c1,c2,…,cM}，ci(i=1,…,M)表示獨立的分類器，M為分類器總數，則

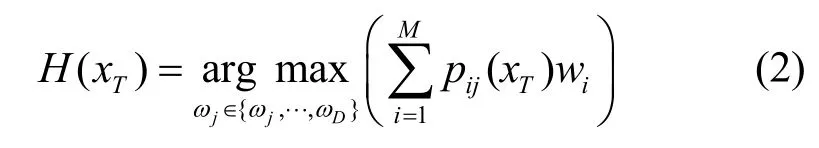
其中，H(xT)表示樣本xT的預測類別，pij(xT)為樣本xT被分類器ci判斷為ωj的概率，wi表示分類器ci的權重。

對于基本加權投票，如果分類器ci對樣本xT的預測為類別ωj，則pij(xT)=1，否則pij(xT)=0。當遇到二分類問題(yn∈{-1,1})時，式(2)可寫為

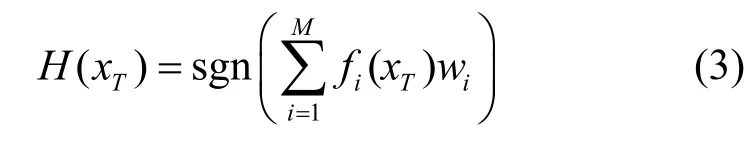
其中，fi(xT)表示樣本xT被分類器ci預測的類別。

對于軟投票系統，根據加權級別不同可分為分類器級別加權、樣本級別加權和類別級別加權[79]。分類器級別加權只對要集成的基學習器分配權重，總體性能良好的基學習器的權重較高；針對每個樣本對分類器影響不同，可對樣本給予適當權重；對于類別加權，考慮到不同子學習器在不同類別上的性能不同，為每個基學習器在不同輸出類別上分配不同的權重。

加權投票可以看作一種優化問題，可采用智能啟發算法解決。Aburomman等[80]提出了一種新的集成構造入侵檢測模型，采用不同K值的K近鄰方法和不同參數的SVM作為基分類器，采用粒子群算法產生的權值對其進行集成。采用局部單峰采樣（LUS,local unimodal sampling）方法作為元優化器，為粒子群優化算法尋找更好的性能參數。Zhang等[81]采用C4.5、樸素貝葉斯（NB,naive Bayesian）、貝葉斯網絡和K近鄰方法作為基分類器，采用差分進化算法確定加權投票的權值。Onan等[82]基于一種多目標優化的差分進化算法確定投票權值，采用邏輯回歸（LR,logistic regression）、樸素貝葉斯、線性判別分析、邏輯回歸和支持向量機作為基學習器，實驗結果表明該方案比傳統的集成學習方法如AdaBoost、Bagging、隨機子空間和多數投票等具有更好的預測能力。Zelenkov等[51]采用GA進行特征選擇的同時，也用其進行權重組合學習。Ekbal等[83]采用GA構造基于加權投票的分類器集合解決命名實體識別（NER,named entity recognition）問題，以最大熵（ME,maximum entropy）、條件隨機場（CRF,conditional random field）和SVM作為基本分類器。結果表明，基于GA的投票集成策略優于單個分類器、3種傳統集成方法和一些現有集成技術。

對于異構集成學習模型，由于不同子模型性能不同，對子模型的選擇是加權投票集成的關鍵問題。除此之外，可能需要同時優化多種度量確定最佳集成組合，采用多目標優化技術是解決此類集成優化的關鍵。

3.6 核函數學習

核方法是機器學習領域有效的學習方法，主要用來解決低維空間線性不可分問題。采用核方法的好處在于可以處理任意維數的特征空間，而不需要計算其到特征空間的映射，避免復雜的內積計算。核函數可表示為一特征空間的內積，假設K(xi,xj)為核函數，向量xi和xj在高維特征空間的內積可表示為K(xi,xj)=<φ(xi),φ(xj)>，其中φ(x)表示向量x到高維空間的映射。任意滿足Mercer定理的函數都可以作為核函數。典型核函數包括線性核函數、多項式核函數、徑向基核函數、sigmoid核函數等，其中徑向基核函數又稱為高斯核函數是最常用的核函數。然而，由于樣本可能包含異構信息或者表示方式不同，使用單個預定義核函數通常是不夠的。因此，存在核組合方法的大量研究，即多核學習（MKL,multiple kernel learning）。不管采用單核學習還是多核學習，都需確定相關核參數，因為其隱式定義了高維特征空間的結構，從而控制最終解決方案的復雜性，對于多核學習還需確定相關核函數系數。線性多核函數是最常見的多核函數形式[84]，如式(4)所示。

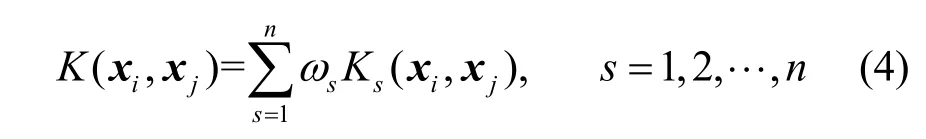
其中，n表示核函數的個數，s表示核函數的序號，sω表示第s個核函數的系數。SVM是核方法成功應用的典型。為了確定核函數及相關參數，大量核方法通常基于SVM展開研究，將目標函數轉化為不同的優化問題，通過不同的優化方法求解。采用智能啟發算法求解核函數不失為一種簡潔的方案。Gauthama等[85]針對SVM參數設置，包括懲罰參數項和高斯核參數以及特征選擇問題，提出一種基于超圖遺傳算法（HG-GA,hypergraph based genetic algorithm）的自適應穩健入侵檢測技術。Zhang等[86]提出采用蟻群優化算法優化SVM相關參數。Kuang等[87-88]分別采用遺傳算法和混沌粒子群優化算法優化SVM相關參數，建立基于KPCA進行特征提取的入侵檢測模型。當前存在的智能啟發算法不斷被改進，Bamakan等[89]提出一種基于時變混沌粒子群優化算法進行特征選擇和確定SVM參數的入侵檢測模型，采用檢測率和誤報率2種度量定義適應度函數。Bao等[90]提出一種基于PSO和模式搜索（PS,pattern search）的memetic框架對SVM參數尋優，其中，PSO用來搜索全局空間，PS進行局部探尋，并采用一種概率選擇策略平衡二者關系。Avci等[91]采用GA優化基于小波核函數的核參數及極限學習機相關系數。

Ma等[84]提出基于自適應蜂群（SABC,self-adaptive artificial bee colony）算法的多尺度高斯核極限學習機模型。采用多種高斯核函數相結合的方式作為核極限學習機的核函數，指出多種高斯核函數的結合比用單一高斯核函數更靈活。SABC用來確定正則化參數和核參數以及多個核函數的權重值。和Ma的分類器相關的多核學習相比，Niazmardi等[92]采用和分類器無關的多核學習方法，提出采用PSO評估組合核和理想核的相似度進行多核學習，采用3種基于核的相似性度量，即核對齊（KA,kernel alignment）、中心核對齊（CKA,centered kernel alignment）和希爾伯特–施密特獨立準則（HSIC,Hilbert-Schmidt independence criterion）進行評估。

多核學習方法假定基礎核函數是預先確定的，目前大多數MKL算法采用復雜的優化技術，只能解決二分類問題[92]；而采用啟發算法進行多核學習可同時優化基本核參數及其組合系數。在已有核函數學習框架中，評估核函數的非線性組合以及核相似性度量是需要進一步研究的方向。

4 結束語

本文結合機器學習算法在實際應用中面臨的問題，對智能啟發算法在機器學習中的應用進行總結，從對神經網絡等參數結構的優化、特征優化、集成約簡、原型優化、加權投票集成和核函數學習等方面介紹智能啟發算法的應用場景，為解決問題提供一個新的思路。采用智能啟法算法解決問題是一個相對較新的領域，常和其他技術相結合使用。另外，智能啟發算法本身也可以直接應用在某一領域，例如傳統的聚類算法一般基于梯度下降法實現，然而由于求解易陷入局部極值，產生的結果并不準確。1990年，研究者們開始嘗試采用自然啟發方法實現聚類，Nanda等[93]研究基于自然啟發式的聚類分析方法近二十年，將單目標函數啟發算法和多目標函數啟發算法在聚類中的應用進行綜述。對啟發算法還有許多新的研究領域。

1)無免費午餐定理指出沒有一種優化方法適用于所有問題，根據具體應用場景研究相適應的新的智能啟發算法是研究者們一直努力的方向。考慮不同算法的優缺點，將不同算法的搜索策略進行組合產生新的算法也是研究者們研究的熱點。

2)智能啟發算法相關參數將不同程度影響算法性能，如何調整參數以提高算法性能是一項重要任務。

3)盡管智能啟發算法在實踐中很有效，但在理論上還沒有經過數學上的分析證明[94]。嘗試用一些數學工具如馬爾可夫鏈理論、動態系統等方法證明算法的有效性是學者們努力的方向。

4)由于深度學習算法訓練時間過長，如何采用智能啟發算法在合理的時間內優化大數據背景下的深度學習模型是一個挑戰[95]。如采用基于GPU并行計算的智能啟發算法或許可加快模型的訓練速度。

5)在科學、工程、工業和商業等領域有許多優化問題待解決，研究某種應用場景下相適合的啟發算法是研究者們要考慮的問題。