串級模糊控制在多變量單級倒立擺中的應用

王 斌，趙 慶，李巾錠

（天津大學 機械工程學院，天津300072）

倒立擺系統是一種典型的多變量、 非線性、強耦合和快速運動自然不穩定系統，其精確控制的研究具有重要的工程背景和實際意義[1-2]。模糊控制在控制具有復雜性、信息量少和高標準性性能等要求的被控對象時具有一定優勢，但模糊控制器的設計等方面還沒有得到很好的解決，對于多輸入變量被控對象，控制規則數會隨輸入變量的增多而成指數增加，嚴重制約著模糊控制器的設計與應用[3-4]。

單級倒立擺有4 個輸入變量，若采用常規模糊控制，模糊控制器的控制規則數量非常大，難以實現。文獻[5]和文獻[6]在研究單級倒立擺解耦的基礎上，分別建立了串級模糊控制系統和串級模糊PID控制系統，但二者并沒有研究模糊控制器的設計。本文在研究單級倒立擺控制方程解耦的基礎上，設計了遺傳算法優化串級模糊控制系統，進行了單級倒立擺的串級模糊控制器自動設計。

1 單極倒立擺系統建模

單級倒立擺結構如圖1 所示。

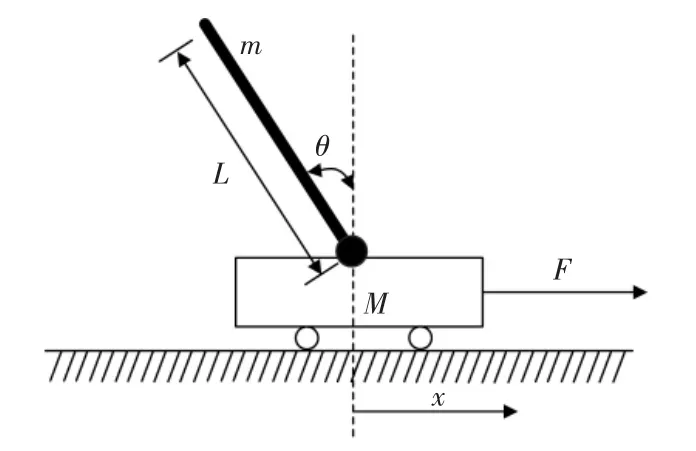
圖1 單極倒立擺結構圖Fig.1 Unipolar inverted pendulum structure

由式（1）可見，位置變量與角度變量為耦合關系，若直接對其進行模糊控制，模糊控制器有4 個輸入變量，若每個輸入變量定義5 個模糊子集，則需要625 個控制規則，模糊控制難以運行。本文為了降低模糊控制的難度，對式（1）首先進行解耦，將統一耦合的倒立擺狀態方程解耦為2 個獨立的狀態方程，分別為角度狀態方程和位移狀態方程：

由此，可對2 個狀態狀態方程直接進行控制。

2 遺傳優化模糊控制系統

2.1 串級模糊控制系統

與常用的Mamdani 型模糊推理模型相比較，TS 模糊控制推理模型更便于定量分析和數學運算，本文采用T-S 模糊控制模型，如圖2 所示。

圖2 雙閉環串級模糊控制系統Fig.2 Double closed loop cascade fuzzy control system

由上圖所示，串級模糊由2 個模糊控制器組成，其中內環模糊控制器控制單級倒立擺的角度，外環模糊控制器控制單級倒立擺的位移，即運用2個模糊控制器分別控制單級倒立擺的角度和位移。

兩個模糊控制器都為二維模糊控制器，設計輸入變量都定義5 個模糊子集，每個模糊子集的隸屬度都為三角形隸屬度：

模糊控制器的規則為配置的反饋極點決定：

其中u（t）=KIx（t），即此時需要的反饋量，K 為此時的反饋控制增益矩陣，由設置的極點進行極點配置求得。

2.2 模糊控制參數優化

運用并行分布補償法設計T-S 模糊控制系統就是將模糊控制器分解為多個線性控制器，將T-S 模糊控制器的每條規則作為一個線性控制器處理。并行分布補償法可分為試湊法和直接法，運用試湊法進行模糊控制器的設計，隨機設計每個線性控制器，將它們聚合在一起，即隨機設計T-S 模糊控制器的控制規則，若隨機設置的T-S 模糊控制系統符合控制要求，則作為設計的T-S 模糊控制系統，否則重新設計。為了實現T-S 模糊控制器的自動設計，采用遺傳算法與試湊法相結合的方法設計T-S 模糊控制系統。即將每個試湊法設計的T-S 模糊控制器轉化為遺傳算法的染色體，并運用遺傳算法對其進行參數優化。

采用自適應遺傳算法對串級模糊控制器的參數進行優化。遺傳算法的輸入和輸出隸屬度都已設計，優化模糊控制器的控制規則。由上文可知，模糊控制器采用極點配置法進行設計，故優化需要的極點。遺傳算法流程如圖3 所示。其中遺傳算法適應度函數、染色體編碼及自適應遺傳操作需要根據實際問題設置。

圖3 遺傳算法流程Fig.3 Genetic algorithm flow chart

（1）初始種群生成

染色體編碼方式的優劣對遺傳算法的運行有重要的影響，本文運用極點配置與并行分配補償法（PDC）結合的方法產生初始染色體。即將整個T-S模糊控制系統分為多個局部線性控制器，并分別運用極點配置法確定各局部線性控制器的反饋參數。雙閉環串級模糊控制器共有50 條控制規則，每條規則代表1 個狀態方程，可運用極點配置法將每個狀態方程的極點設定為所需要的。每組極點為共軛極點，具有負實部，以這組共軛極點的實部絕對值和虛部的模表示。采用十進制編碼，每條染色體有100 個數組成。根據上述編碼方法及設定的種群中個體數量，進行初始種群生成。

（2）適應度函數的建立

遺傳算法的適應度函數是遺傳進化的依據，其確定直接影響著控制模型的優化效果。單級倒立擺的控制需要具有快速性和穩定性，通過多次仿真試探，適應度僅函數以單級倒立擺的小車位移和擺桿角度及為參數標準，確定適應度函數中的各項參數。改進遺傳算法的適應度函數如下式：

式中：T 代表采樣周期；N 代表采樣次數，仿真時間為N*T；j 為采樣次數；x1（j）和x3（j）分別為第j 次采樣時單級倒立擺輸出的位移和角位移。

（3）自適應遺傳操作

首先是選擇操作中采用最優保存策略，保留上一代中的最優個體，直接進入下一代，代替下一代的最差個體。同時，為了解決遺傳算法的早熟問題，提高遺傳算法的魯棒性，本文采用了自適應遺傳算法，自適應交叉率和變異率隨著個體的適應度在種群平均適應度和最大適應度之間進行調整，并設計了自適應交叉率和變異率：

3 實驗仿真分析

根據上文設計的模糊控制系統，在Matlab 環境下進行雙閉環串級模糊控制器的設計與仿真。取倒立擺的擺桿的初始擺角位移和角度分別為0.2 rad 和0 rad/s，取位移和速度分別為0.1 m 和0.1 m/s。小車的質量和擺桿的質量分別為2 kg 和0.02 kg，擺桿長為0.5 m，小車的摩擦系統為0.1 N/m/s。將上述參數代入控制系統中，運用設計方法對其進行優化，設定遺傳算法的初始種群有100 個個體，進化終止代數為100 代，遺傳算法的優化過程如圖4 所示。

圖4 遺傳算法優化過程Fig.4 Genetic algorithm optimization process diagram

由上圖可知，改進遺傳優化過程在前30 代收斂很快，過了30 代，基本趨近穩定，說明改進遺傳算法有良好的優化效果。

將優化的控制器參數及單級倒立擺參數代入雙閉環模糊控制模型中，對其進行仿真。同時運用同一遺傳算法優化雙閉環反饋控制系統，將其優化控制結果與串級模糊控制結果相比較，倒立擺的位移控制和角度控制結果圖如圖5 和圖6 所示。

由圖5 和圖6 中的雙閉環串級模糊控制系統和常規雙閉環控制系統的控制結果對比可知，相比于常規雙閉環控制器，雙閉環串級模糊控制系統減小了系統的超高量，縮小了系統的輸出振蕩，縮短了穩定時間，具有更好的動態性能。

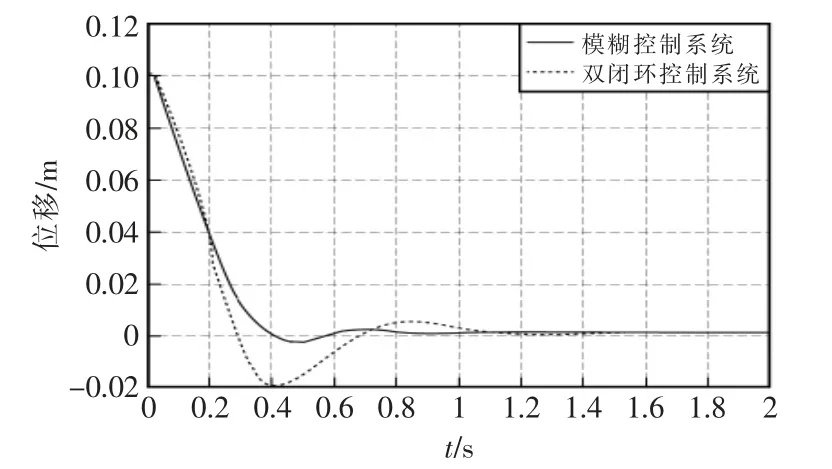
圖5 小車位移控制對比圖Fig.5 Cart displacement control comparison diagram

圖6 擺桿角位移控制對比圖Fig.6 Pendulum angle displacement control comparison diagram

4 結語

單級倒立擺系統的精確控制具有重要的工程背景和實際意義，對其變量解耦以降低控制模型的復雜度和難度是一個重要的研究方向。本文以單級倒立擺控制模型的變量解耦為基礎，成為實現了單級倒立擺的雙閉環串級模糊控制，將有利于模糊控制在多變量控制模型中應用發展。