基于有限元/邊界元的雙層周期加筋板聲輻射分析

周海安，修孝廷，孟建兵

(1.山東理工大學(xué) 機(jī)械工程學(xué)院，山東 淄博 255049;2.徐州徐工礦山機(jī)械有限公司，江蘇 徐州 221000;

聲振問題包含結(jié)構(gòu)振動的相互作用和聲結(jié)構(gòu)的耦合效應(yīng)，其在工程應(yīng)用中具有重要的意義。雙層周期加筋板在現(xiàn)代建筑、汽車、船舶和航空航天等行業(yè)應(yīng)用越來越廣泛。對加筋板的振動聲輻射研究，早期主要是以單層無限大具有相同加強(qiáng)筋的薄板為研究對象。Laulagnet[1]研究了簡支無限平板的聲輻射問題，在一系列簡支平板模型中發(fā)展出了聲壓跳動量和平板位移量。Berry等[2]采用瑞利—李茲法(Rayleigh-Ritz method)研究了無限障板中流體加載下單層加筋板的振動和聲輻射。近年來，金葉青等[3]采用傅立葉變換技術(shù)，在波數(shù)域?qū)辛ψ饔孟碌膯螌訜o限大加強(qiáng)筋板進(jìn)行了輻射聲壓的數(shù)值求解。金葉青，姚熊亮等[4]還對均勻流中剪切變形的加筋層合板的振動及聲學(xué)特性通過數(shù)值截斷的方法進(jìn)行了分析，并驗證了其數(shù)學(xué)模型的正確性。周海安等[5]則通過一種高效的半解析方法對簡諧面力作用下的雙周期正交加筋板的振動及聲輻射性質(zhì)進(jìn)行了理論預(yù)測與分析，并考慮了加強(qiáng)筋的扭轉(zhuǎn)作用對結(jié)構(gòu)的影響。基于空間諧波法及虛功原理，陳海龍等[6]分析了單向周期加筋板的隔聲性能,而龐福振等[7]則繼續(xù)分析了無限大正交周期加筋層合板的隔聲性能。尹劍飛等[8]則基于統(tǒng)計能量法和聲波傳播的相關(guān)理論研究了單向周期加筋板中彎曲波的傳播特性。Takahashi[9]研究了在諧點力作用下周期性連接無限雙層結(jié)構(gòu)的聲輻射問題，并計算出了兩個不同結(jié)構(gòu)的聲輻射功率。Ma等[10]運用解析方法研究了雙層周期加筋板結(jié)構(gòu)聲傳輸?shù)闹鲃涌刂茩C(jī)理，并對聲傳輸機(jī)理給出了物理解釋。本文主要用有限元和邊界元相結(jié)合的方法研究雙層周期加筋板結(jié)構(gòu)的聲輻射特性，計算在諧力作用下結(jié)構(gòu)表面振動的輻射聲場，為揭示雙層周期加筋板結(jié)構(gòu)聲學(xué)特性提供一種數(shù)值方法。

1 結(jié)構(gòu)有限元方程

有限元的基本方程可以用微分方程法和變分法推導(dǎo)得到，以下采用變分法中的Hamilton原理推導(dǎo)有限元基本方程[11]

(1)

式中：M為結(jié)構(gòu)總質(zhì)量矩陣；C為總阻尼矩陣；K為總剛度矩陣；Q為總體力系數(shù)矩陣；H為總面外力系數(shù)矩陣。當(dāng)外力項F、p、Fc均為零時，則式(1)變?yōu)榍蠼饨Y(jié)構(gòu)振動模態(tài)方程

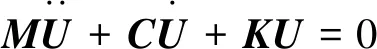
(2)

對于時間因子為ejωt的情況，式(2)變?yōu)?/p>

K+jωC-ω2Mu=0

(3)

即有

K+jωC-ω2M=0

(4)

式(4)為結(jié)構(gòu)自由振動模態(tài)本征頻率方程。若結(jié)構(gòu)無阻尼，則變?yōu)?/p>

K-ω2M=0

(5)

本文對雙層加筋板中的板結(jié)構(gòu)采用基于Mindlin板彎曲理論的殼單元進(jìn)行有限元離散，筋結(jié)構(gòu)采用了考慮剪切變形的梁單元，邊界元采用與殼單元相對應(yīng)的四邊形四節(jié)點等參單元。

2 聲學(xué)邊界元

簡諧振動情況下的聲壓為

p(t)=Pejωt

(6)

理想流體介質(zhì)中聲學(xué)波動方程為

(7)

將式(6)代入式(7)，得

(8)

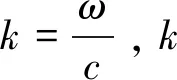
(9)

從而得到可壓縮流體小振幅下聲學(xué)波動Helmholtz方程。

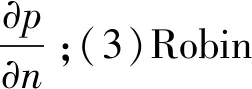
對于空間中某一封閉曲面結(jié)構(gòu)，其表面為S，當(dāng)封閉結(jié)構(gòu)振動時，在結(jié)構(gòu)內(nèi)部或結(jié)構(gòu)外部流體域B'中產(chǎn)生結(jié)構(gòu)聲輻射。考慮邊界條件，對式(9)使用加權(quán)余量法，并采用基本解自由場格林函數(shù)

(10)

式中：

P為空間中任意點；Q為S上任意點；G(P,Q)為自由場格林函數(shù)。

2.1 直接邊界元

可壓縮理想流體中，根據(jù)小振幅振動的Helmholtz方程、流固面邊界條件及在無限遠(yuǎn)處的Sommerfeld輻射條件，可以得到Helmholtz邊界積分方程[12]

C(P)p(P)=

(11)

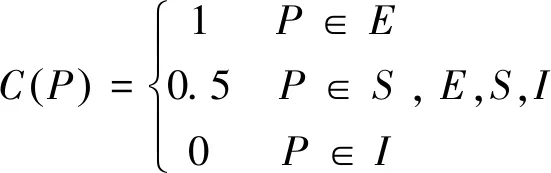
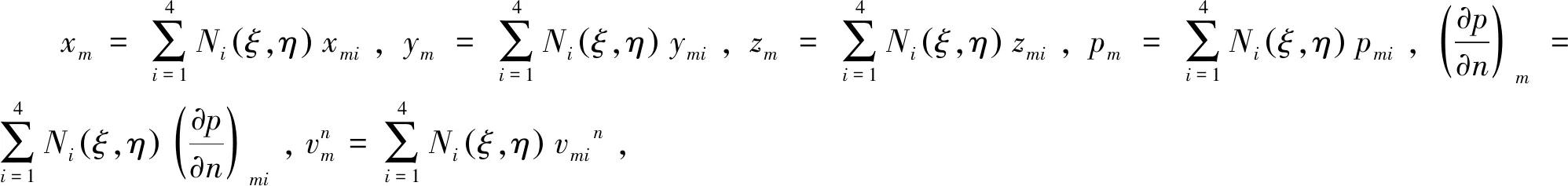
(12)

式中：n的下標(biāo)Q表示在Q點處的法向?qū)?shù)；Ni(ξ,η)表示第m個單元的結(jié)點i處的插值函數(shù)在(ξ,η)處的取值。

將式(12)表達(dá)為與邊界結(jié)點相對應(yīng)的4M個離散方程，并在整個邊界S上積分化為在各個單元上的積分，用等參元可表示為

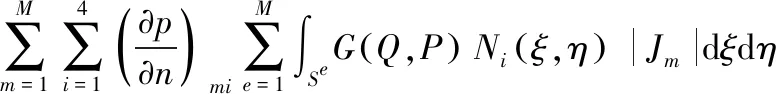
(13)

式中:e為單元序號，Se為單元的區(qū)域;|Jm|是將四邊形變換為ξη平面的正方形的變換行列式。

式(13)可表達(dá)為矩陣形式

(14)

其中：

(15)

(16)

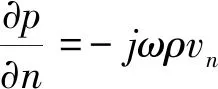
Ap=Cvn

(17)

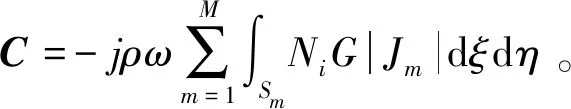
在將邊界元模型導(dǎo)入聲學(xué)分析軟件(如SYSNOISE)中時，A和B會自動生成，結(jié)點上的法向振速已知時，通過求解(17)式可得出節(jié)點的聲壓值。之后可以求出邊界上包含聲壓在內(nèi)的其它聲場參數(shù)，進(jìn)一步利用邊界積分公式，就可以對聲場內(nèi)有關(guān)聲場參數(shù)進(jìn)行分析計算。

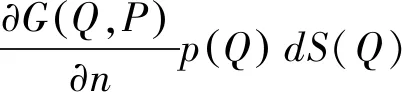
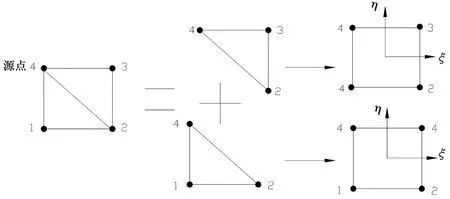
圖1 四節(jié)點線性元引入退化元Fig.1 The linear 4-node element introduced degenerate element

結(jié)構(gòu)表面上的聲壓、聲速和聲強(qiáng)等通過求解系統(tǒng)方程得到后，直接用Helmholtz積分方程(P∈E)，即可得到流體介質(zhì)中任一點P處的聲壓。

2.2 間接邊界元

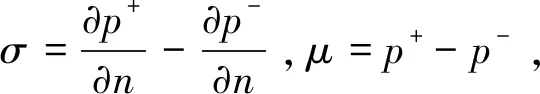
(18)

當(dāng)場點P在邊界單元的模型上時，根據(jù)流固面Neumann邊界條件可得

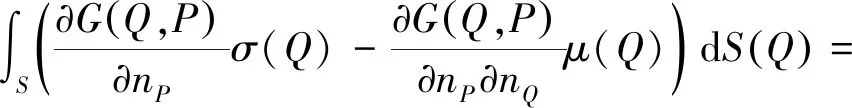
-jρωvn(Q)

(19)

式中：?nP，?nQ為結(jié)構(gòu)表面上點P和Q處的內(nèi)法向單位矢量；vn(Q)為Q點處的法向振速。

邊界單元模型上未知變量可用該模型上節(jié)點的未知變量及其形函數(shù)表示。利用變分原理，可推導(dǎo)出間接邊界元一般形式

AX=Fa

(20)

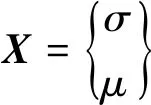
3 結(jié)構(gòu)有限元和間接邊界元耦合方程

結(jié)構(gòu)—聲耦合分析是將結(jié)構(gòu)的有限元方程和聲場的邊界元方程耦合起來。結(jié)構(gòu)—聲耦合的方程[14]可表示為

(21)

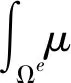
因此，本文無阻尼聲輻射問題所要求解的方程如下：

(22)

將結(jié)構(gòu)有限元和聲邊界元模型的單元進(jìn)行離散，有限元結(jié)構(gòu)模型劃分為M個單元，在每一個單元上采取L個積分點，耦合矩陣變換到單元的局部物理坐標(biāo)系中的形式如下：

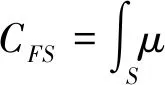
(23)

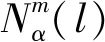
(24)

(25)

將式(24)和式(25)代入式(23)中，整理可得

(26)

結(jié)構(gòu)有限元模型的節(jié)點和單元可分成與邊界元模型公共的部分和非公共的部分，只有公共部分的結(jié)構(gòu)節(jié)點和單元才參與計算耦合矩陣。

在通過聲學(xué)分析軟件求解式(22)得到模型表面的未知變量u和X后，可利用式(18)計算得到任意場點處的聲壓。

聲壓級[15](Sound Pressure Level, SPL)定義為聲壓的有效值與基準(zhǔn)聲壓的有效值之比，然后取20倍常對數(shù)，單位dB，其表示形式如下：

(27)

式中：pP為所得測量聲；pr為參考聲壓，pr=2×10-5Pa，即人耳對1 kHz空氣聲所能感覺到的最低聲壓。

4 算例

以如圖2所示的雙層雙周期正交加筋板計算模型為例：板厚均為t，筋高為H，寬為W，周期數(shù)為n，x方向的間距為lx，y方向的間距為ly，板間距為h，板材與筋材料相同。計算中取：鋼材密度為7 800 kg/m3，彈性模量為210.0 GPa，泊松比為0.3，t=0.005 m，H=0.1 m，W=0.01 m，lx=ly=0.2 m，h=0.3。在有限元中平板用SHELL63單元，筋用BEAM188單元，流體單元采用Fluid30，有限元模型如圖3所示。

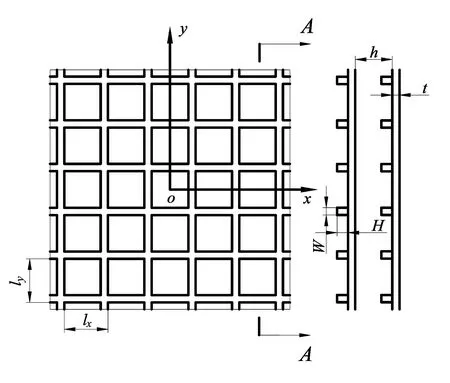
圖2 雙層雙周期加筋板示意圖Fig.2 Schematic of double periodical beam-stiffened panels

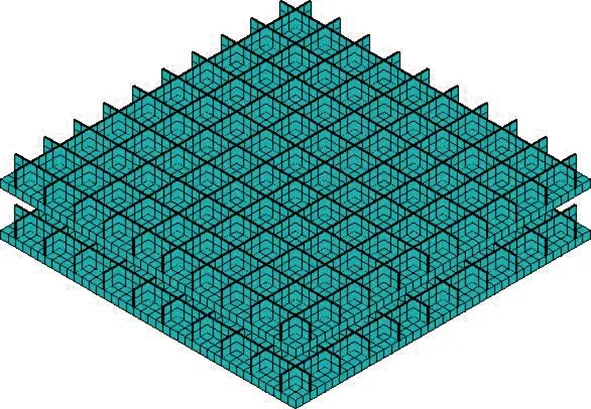
圖3 部分雙周期加筋板有限元模型Fig.3 Partial FEM model of double periodicalbeam-stiffened panels

在周期結(jié)構(gòu)的下層周期加筋板上施加力幅值為{Fe}=1 000 N的簡諧面力，兩周期加筋板之間充滿水介質(zhì)，水的密度ρ=1 000 kg/m3，水中的聲速c=1 500 m/s。在四面的邊界上施加周期對稱邊界條件；在有限元中進(jìn)行諧分析，分析的頻率范圍為20～2 000 Hz，步長為20 Hz。

將諧分析結(jié)果導(dǎo)入到聲學(xué)邊界元軟件中，可計算出周期結(jié)構(gòu)在水中任意點處的聲壓。本文計算了距雙層周期加筋板上層周期結(jié)構(gòu)0.1 m處(見圖4)聲壓隨頻率變化的聲壓級(見圖5)，可以看出在800 Hz和1 200 Hz附近處場點的聲壓級較大，說明在該頻率段處周期結(jié)構(gòu)的輻射能力強(qiáng)。

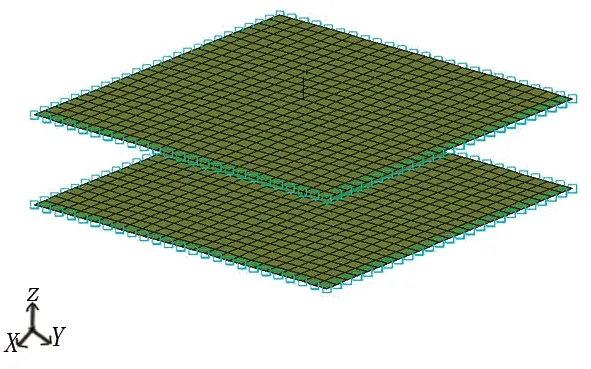
圖4 場點位置(垂直距離為0.1m)Fig. 4 The location of field point

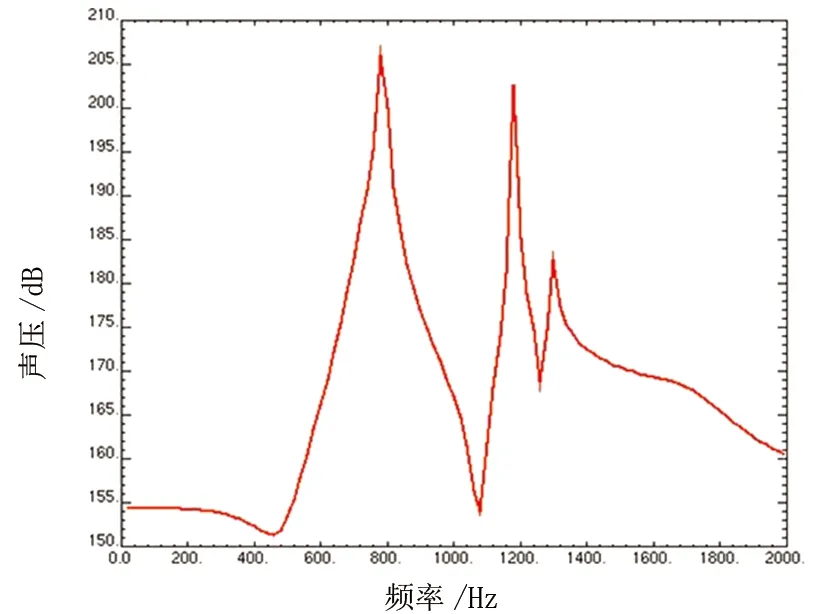
圖5 雙層周期加筋板的輻射聲壓級圖Fig.5 Sound pressure level of double periodical beam-stiffened panels

以如圖6所示的雙層雙周期斜交成正六邊形加筋板模型為例，參數(shù)和邊界條件不變，有限元模型見圖7。在距雙層雙周期斜交成正六邊形加筋板結(jié)構(gòu)0.1 m處的聲壓隨頻率變化的聲壓級曲線如圖8所示，可以發(fā)現(xiàn)在800 Hz和1 100 Hz處場點的聲壓級較低，說明在該頻率段處周期結(jié)構(gòu)的輻射能力弱。

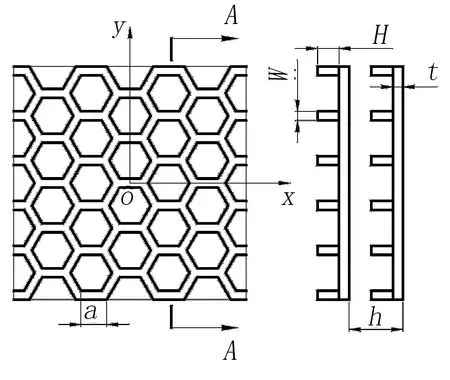
圖6 雙層雙周期斜交成正六邊形加筋板示意圖Fig.6 Schematic of double dual-periodical hexagonal beam-stiffened panels

圖7 雙層雙周期斜交成正六邊形加筋板有限元模型Fig. 7 FEM model of double dual-periodical hexagonal beam-stiffened panels

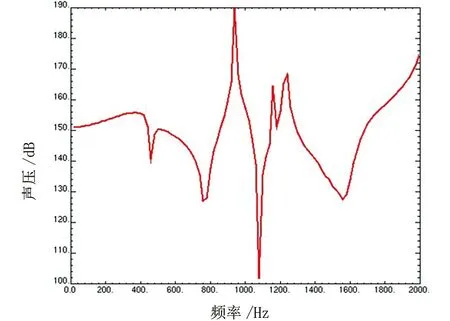
圖8 雙層雙周期斜交成正六邊形加筋板的輻射聲壓級圖Fig.8 Sound pressure level of double dual-periodical hexagonal beam-stiffened panels

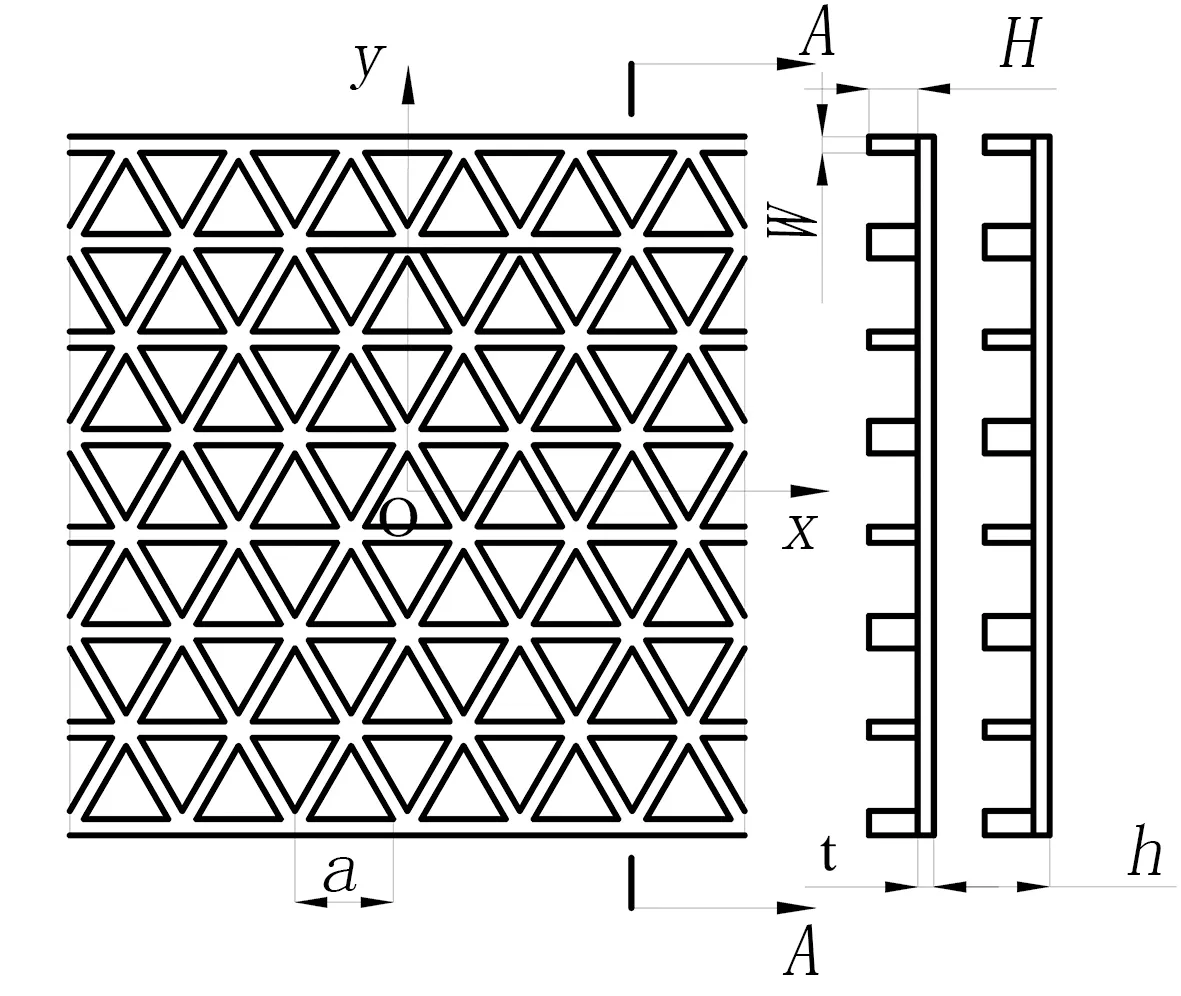
圖9 雙層雙周期斜交成正三角形加筋板示意圖Fig.9 Schematic of double dual-periodical trigonal beam-stiffened panels

以如圖9所示的雙層雙周期斜交成正三角形加筋板模型為例，參數(shù)和邊界條件不變，有限元模型見圖10。在距雙層雙周期斜交成正三角形加筋板結(jié)構(gòu)0.1 m處的聲壓隨頻率變化的聲壓級曲線如圖11所示。可以發(fā)現(xiàn)在800 Hz和1 600 Hz處場點的聲壓級較低，說明在該頻率段處周期結(jié)構(gòu)的輻射能力弱；在1 100 Hz和1 700 Hz處場點的聲壓級較高，聲輻射能力強(qiáng)。這與結(jié)構(gòu)的固有頻率相關(guān)，結(jié)構(gòu)的固有頻率受結(jié)構(gòu)密度、剛度、尺寸及邊界條件等因素影響。一般情況下，當(dāng)外部激勵力的頻率與結(jié)構(gòu)的固有頻率相等或接近時，則結(jié)構(gòu)的聲輻射增大；當(dāng)外部激勵力的頻率與結(jié)構(gòu)的固有頻率相差較大時，則結(jié)構(gòu)的聲輻射減小。

圖10 雙層雙周期斜交成正三角形加筋板有限元模型Fig.10 FEM model of double dual-periodical trigonal beam-stiffened panels

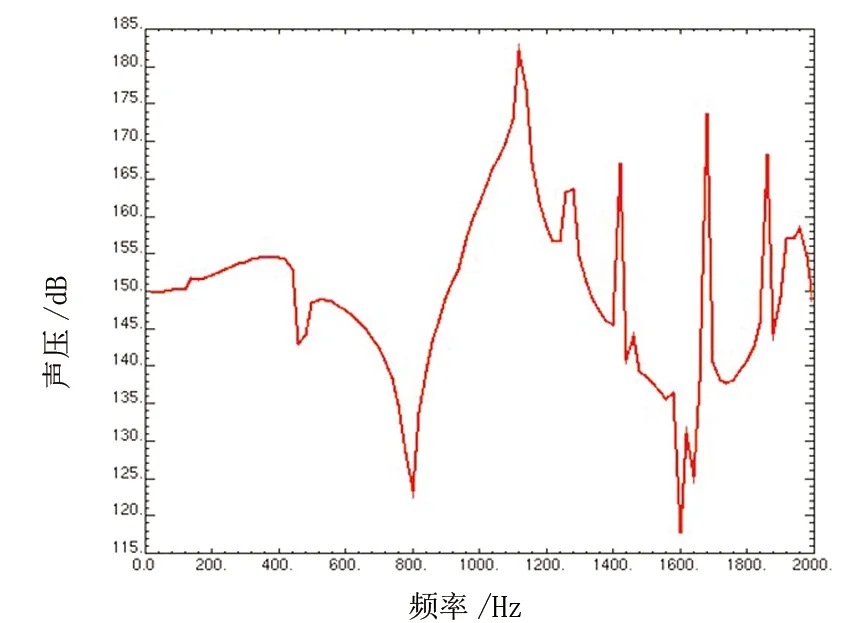
圖11 雙層雙周期斜交成正三角形加筋板的輻射聲壓級圖Fig.11 Sound pressure level of double dual-periodical trigonal beam-stiffened panels

5 結(jié)束語

采用有限元和邊界元相結(jié)合的數(shù)值方法，建立了雙層周期加筋板在低頻諧力作用下，聲波在水中輻射的計算模型，并利用該模型計算研究了雙層周期加筋板的聲輻射特性。雙層周期加筋板結(jié)構(gòu)在簡諧面力的作用下，振動呈現(xiàn)出一定的周期性，在特定的頻率范圍內(nèi)或特定頻率附近處時，周期加筋板結(jié)構(gòu)振動位移大于其他頻率處，為了增強(qiáng)(或減弱)周期結(jié)構(gòu)的聲輻射能力可以接近(或避開)特定的頻率。該方法的最大優(yōu)點是可以計算任意復(fù)雜結(jié)構(gòu)的輻射聲場，數(shù)值計算的實例表明該方法具有一定的應(yīng)用前景.