參數不匹配的時滯憶阻神經網絡的指數同步
,
(1.山東科技大學 數學與系統科學學院, 山東 青島 266590;2.山東科技大學 電氣與自動化工程學院, 山東 青島 266590)
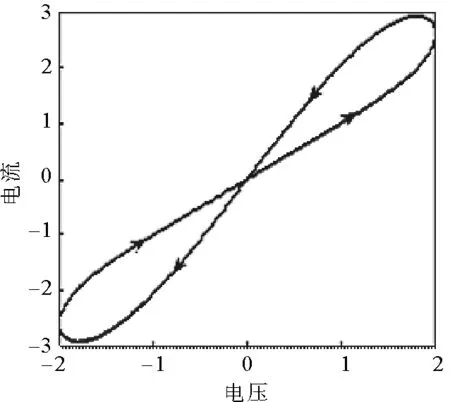
圖1 憶阻器伏安特性曲線Fig.1 Current-voltage characteristic of memristor
1971年,電路理論學家蔡少棠根據概念的對稱性首次提出用憶阻器來描述電荷與磁鏈之間的關系[1]。2008年,美國惠普公司實驗室首次實現了具有記憶功能的TiO2納米級憶阻器[2]。如圖1所示,憶阻器展示了“8”字型伏安特性曲線,其憶導值依賴于電壓或電流的作用時間。與傳統電阻相比,憶阻器具有記憶特性。因此,越來越多的學者用憶阻器代替傳統的電阻元件來模擬大腦神經元突觸,用以構建基于憶阻的人工神經網絡——憶阻神經網絡。相較于傳統的神經網絡,憶阻神經網絡能夠更好地應用于神經元學習、聯想記憶和人工智能[3-6]。
近年來,憶阻神經網絡的動力學行為如穩定性[7]、耗散性[8]、鎮定[9]同步等研究受到越來越多研究人員的重視。文獻[7]通過平均駐留時間和李雅普諾夫泛函方法研究了憶阻神經網絡的穩定性;文獻[8]基于李雅普諾夫理論得到了憶阻神經網絡的耗散性條件;文獻[9]考慮執行器飽和情況下憶阻神經網絡的鎮定問題。而憶阻神經網絡的同步因其在保密通信等領域的潛在應用,更成為研究的熱點[10-14]。值得注意的是,由于憶阻連接權重直接依賴于系統的狀態,并且由其定義可以看出其不連續特性,這使得憶阻神經網絡本質上為一類切換系統。因此,相較于傳統的連續型神經網絡,憶阻神經網絡的同步控制實現起來更加困難。文獻[10]通過設計靜態和動態耦合控制器研究了時滯憶阻神經網絡的指數同步;文獻[11]基于“Stop and Go”自適應控制策略研究了帶有不確定參數的時滯憶阻神經網絡的漸近同步;文獻[12]通過設計新的切換控制器研究了憶阻神經網絡的有限時間同步;文獻[13]基于新的魯棒性分析方法研究了時滯憶阻神經網絡的指數同步;文獻[14]基于區間矩陣法研究了時滯憶阻神經網絡的完全同步。
神經網絡可以由超大規模集成電路實現。然而,在憶阻神經網絡硬件電路實現中,由于不可避免地存在參數攝動、外部干擾等因素,驅動系統和響應系統的電路參數之間不可避免地存在不匹配現象。文獻[10-14]得到的同步結果都是基于驅動-響應系統之間參數完全相同的理想條件下得到的,其同步判據并不能被直接應用到實際中。目前,關于參數不匹配時滯憶阻神經網絡的同步控制鮮少有相關研究結果。
基于以上分析,研究了參數不匹配時滯憶阻神經網絡的同步問題。主要內容如下:①通過微分包含和集值映射理論,將不連續的憶阻神經網絡轉化為帶有區間參數的不確定性系統;②根據憶阻神經網絡的切換特性和參數不匹配情況,設計了新的切換控制器;③基于李雅普諾夫穩定性理論,構建了李雅普諾夫泛函,通過不等式放縮技術得到了確保驅動-響應系統實現完全同步的充分性條件;④仿真結果驗證了理論結果的正確性。
1 模型與問題描述
基于文獻[10-14],考慮驅動-響應系統分別為下面一類時滯憶阻神經網絡:
(1)
(2)
其中,1≤i≤n,n表示神經元的數量;xi(t),yi(t)分別表示第i個神經元的狀態;τ表示時間延遲;fj(·)表示激活函數,且滿足fj(0)=0;ui(t)表示所要設計的控制器;
表示憶阻連接權重,其表達式分別為
,
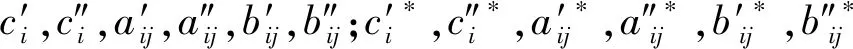
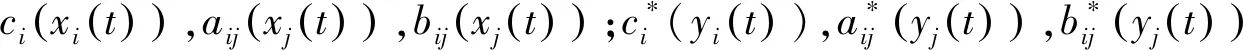
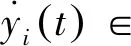
ui(t),
其中:
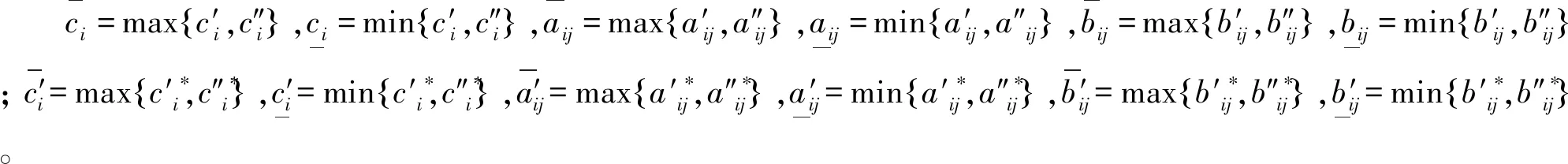
基于可測選擇定理[17],存在ηi(xi(t))∈co[ci(xi(t))],γij(xj(t))∈co[aij(xj(t))],ρij(xj(t))∈
使得
(3)
(4)
將式(3)、(4) 表示為向量形式
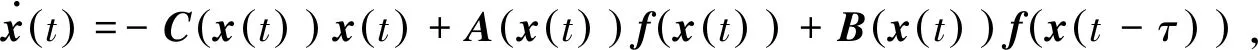
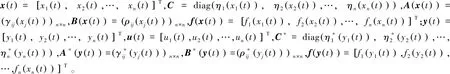
為了保證驅動-響應系統(1)~(2)解的存在性,激活函數fj(·)滿足如下假設:
假設1.1激活函數fj(·)滿足李普希茲條件和有界性假設,即存在Lj>0,Mj>0,1≤j≤n,
使得對任意的u∈R,v∈R,有
|fj(u)-fj(v)|≤Lj|u-v|,
|fj(u)|≤Mj。
假設1.2驅動系統狀態滿足混沌的有界性假設,即存在Ni>0,1≤i≤n,使得
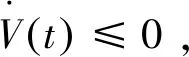
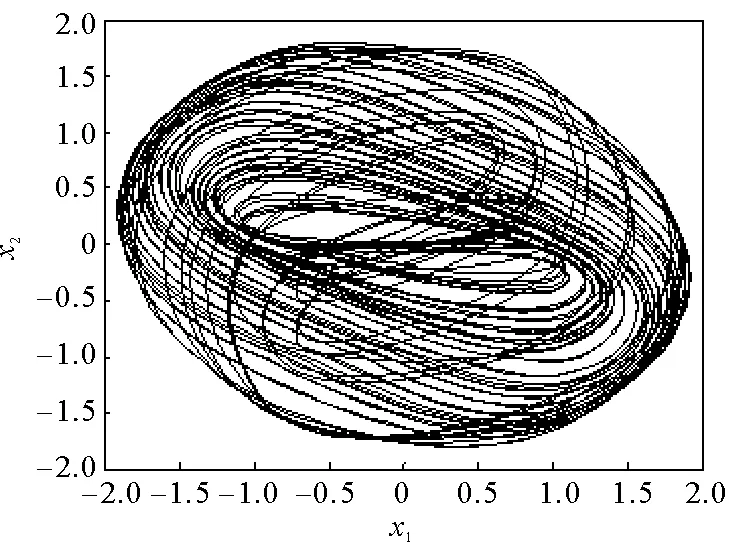
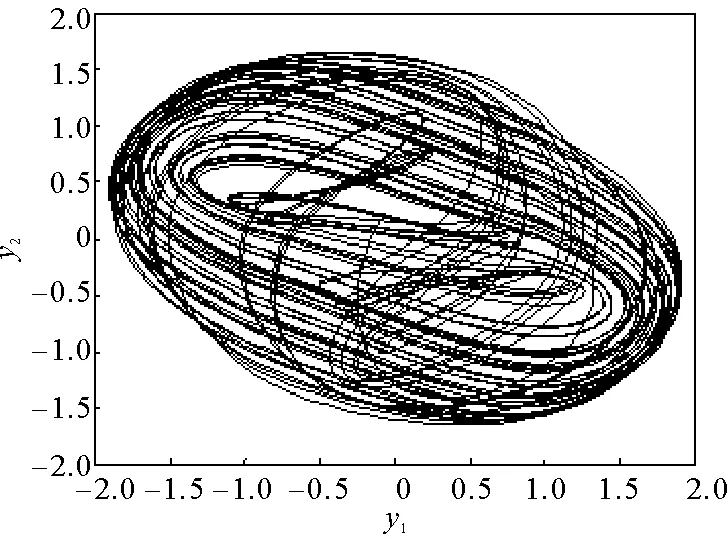
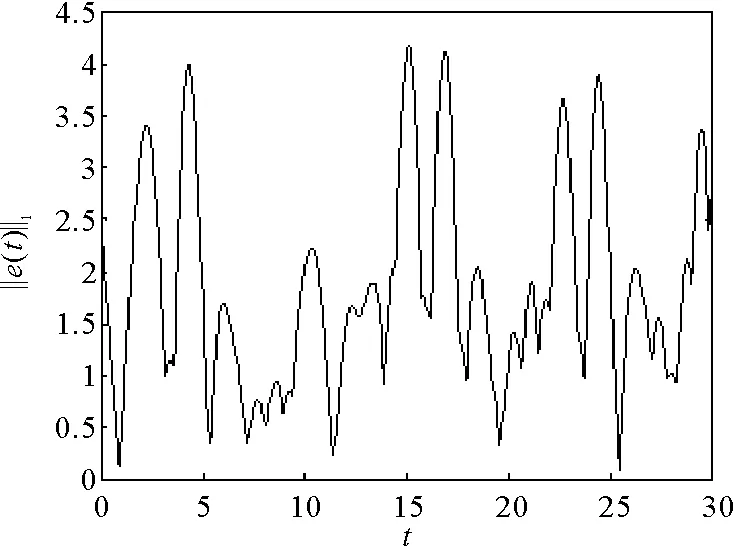
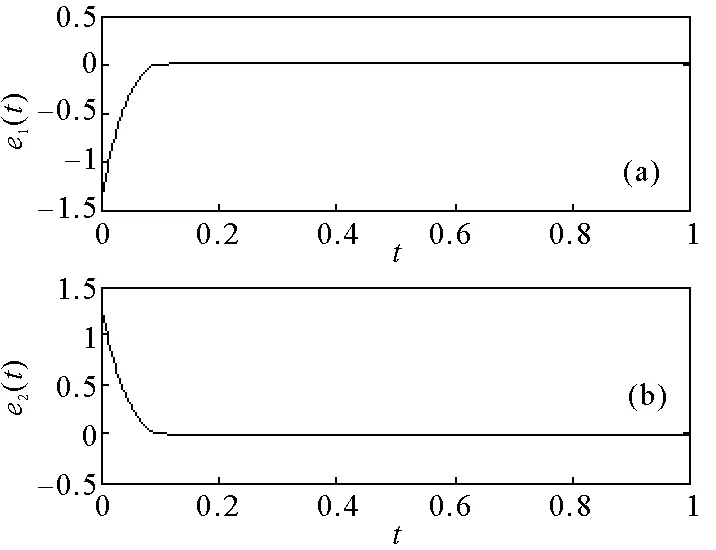
|xi(t)| ei(t)=yi(t)-xi(t)。 切換控制器設計 ui(t)=-kiei(t)-qisign(ei(t))。 (5) 由式(3)~(5)可得誤差系統方程: (6) 其中,φj(ej(t))=fj(yj(t))-fj(xj(t)),φj(ej(t-τ))=fj(yj(t-τ))-fj(xj(t-τ))。 誤差系統的初始值為 ei(s)=φi(s),-τ≤s≤0。 其中,φi(s)=ωyi(s)-ωxi(s)∈C([-τ,0],R)。 由于驅動-響應系統之間存在參數不匹配情況,定義參數誤差: 2.1 實驗組前哨淋巴結檢測結果 試驗組有30例前哨淋巴結均在中央區找到,快速冰凍結果轉移陽性,加做單側頸淋巴結清掃(Ⅱ~Ⅳ區)。試驗組均出現甲狀腺均勻黑染,Ⅵ區淋巴結呈結節樣黑染,未出現片狀黑染,喉返神經未出現黑染,無納米碳外溢影響術野現象發生,見圖1A至圖1C。 定義1.1誤差系統(6)在控制器(5)作用下是指數穩定的,如果存在θ≥1,β>0,滿足以下條件: 其中,ωx(s)=[ωx1(s),ωx2(s),…,ωxn(s)]T,ωy(s)=[ωy1(s),ωy2(s),…,ωyn(s)]T。 定理2.1如果假設1.1和假設1.2成立,且存在常數ri>0,1≤i≤n,滿足以下兩個條件: 證明:構造如下李雅普諾夫泛函: (7) 對V(t)求導可得: 根據定理2.1的條件(i)和(ii)可得 即V(t)為單調不增的,故 其中R=diag(r1,r2,…,rn),L=diag(L1,L2,…,Ln),λmax(·)表示矩陣的最大特征值,λmin(·)表示矩陣的最小特征值。 因此,由方程(7)可得 即 顯然 根據定義1.1可得,誤差系統(6)取得指數穩定,即驅動-響應系統(1)~(2)實現指數同步。 考慮二維驅動系統,fj(xj)=tanh(xj),j=1,2,τ=1,ωx(s)=(0.8,-0.5)T,s∈[-1,0],憶阻連接權重為: 考慮二維響應系統,fj(yj)=tanh(yj),j=1,2,τ=1,ωy(s)=(-0.6,0.8)T,s∈[-1,0],憶阻連接權重為: 圖2 驅動系統混沌吸引子Fig.2 Chaotic attractor of the drive system 圖3 響應系統混沌吸引子Fig.3 Chaotic attractor of the response system 圖4 不加控制器時時域圖形 Fig.4 Time response of without controller 圖5 施加控制器時e1(t)、e2(t)時域圖形Fig.5 Time response of e1(t),e2(t)when the controller is applied 同理,當q1≥1.362,q2≥1.67時,滿足定理2.1中條件(ii),其中Δγ11=0.2,Δρ11=0.2,Δγ12=0.3,Δρ12=0.3,Δη1=0.2;Δγ21=0.2,Δρ21=0.3,Δγ22=0.3,Δρ22=0.3,Δη2=0.3。 則根據定理2.1,在所設計的切換控制器條件下,驅動-響應系統能夠取得完全同步。如圖5所示,在控制器的作用下,e1(t)、e2(t)隨著時間逐漸趨于0。如圖6所示,驅動-響應系統隨著時間的推移相軌跡完全重合,即驅動-響應系統實現了指數同步。 討論了兩個時滯憶阻神經網絡在參數不匹配情況下的指數同步問題。設計了切換控制器,消除了系統參數不匹配帶來的額外誤差。選取相應的李雅普諾夫泛函,利用不等式放縮技巧得到了指數同步的充分條件。仿真結果驗證了理論的正確性。2 主要結果
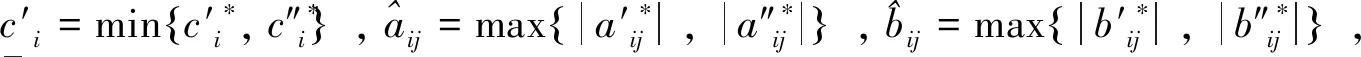
3 仿真結果
4 結論

