具有腐蝕缺陷的輸氣管道的可靠性分析

孫萍萍

中國石化勝利油田分公司濱南采油廠

隨著國民經濟的持續發展，各地的地鐵系統以及高壓輸電系統也在不斷建設，地鐵和高壓輸電系統在運行過程中會有直流雜散電流流入、流出，當電流以金屬管道作為導體形成回路時管道將面臨嚴重的腐蝕危害。在西氣東輸一線、二線等大型工程中，輸氣管道大多采用埋地敷設的方式，由于輸氣管道會穿越部分一線、二線城市，不可避免地會受到雜散電流的干擾而產生腐蝕，在管道敷設以及服役過程中，會在局部產生應力集中現象，最終將會導致管道失效。近年來國內外學者通過可靠性理論對管道進行了大量的研究[1]，如帥健[2]將影響管道剩余壽命的各種因素看成是分布各異的隨機變量，建立了預測管線失效的概率數學模型，并研究了腐蝕速率、缺陷深度、管道壁厚和工作壓力等因素對管線可靠性的影響；張廣利等[3]引入可靠性理論，利用蒙特卡洛模擬技術研究管道可靠度隨缺陷尺寸變化的規律，以及通過敏感性分析，對比評價參數對管道安全可靠性的影響，并進行排序，建立含腐蝕缺陷管道評價準則的概率評價方法；AHAMMED[4]研究了含局部腐蝕管道的可靠性。

本文介紹了輸氣管道可靠度的計算方法，根據ASME B31G—2009給出了基于B31G的極限狀態方程，采用Monte-Carlo法對目前西氣東輸使用最為廣泛的X80管道進行了可靠度評估，最后分析了不同參數對管道可靠度影響的敏感性。

1 具有缺陷的輸氣管道的可靠度計算

采用B31G—2009標準對具有缺陷的管道進行可靠性分析，功能函數為

式中：Z為極限狀態方程；M為Folias膨脹系數；pf為失效壓力，MPa； pop為運行壓力，MPa；t為管道壁厚，mm；SMSY為材料的屈服強度，MPa； D為管道外徑，mm；d為腐蝕缺陷深度，mm；L為腐蝕缺陷長度，mm。

Z＞0時，管道處于安全狀態；Z=0時，管道處于極限狀態；Z＜0時，管道則為失效狀態。

可靠性也被稱之為可靠度，是指產品在規定的時間以及條件下能否完成預定功能的度量。基于可靠性的設計和評價方法的核心在于極限狀態方程的計算，可以通過多種方法完成，為了回避管道可靠度分析中的數學困難，不考慮功能函數的復雜性，將采用Monte-Carlo法對管道進行可靠性分析。

由概率定義可知，某事件的概率可以用大量試驗中該事件發生的頻率來估算，當樣本容量足夠大時，可以認為該事件的發生頻率即為其概率。因此，可以先對影響其可靠度的隨機變量進行大量的隨機抽樣，然后把這些抽樣值一組一組地代入功能函數式，確定結構是否失效，最后從中求得結構的失效概率。

應用Monte-Carlo法根據管道的基本參數產生1組符合隨機變量分布的1個樣本Xi（i=1，2，…， k），代入到極限狀態方程Z=g(x1，x2，…，xk)中，可以計算出1個隨機數。通過此方法反復進行n次模擬，可以得到n個隨機數，最后統計出大于零的數量為m，當n→∞時，根據伯努利大數定理及正態隨機變量的特性，可以得到可靠度為m/n。對于輸氣管道，具體的操作流程見圖1，由于取值的數量較多，在Matlab程序中通過編程實現可靠度的計算，為了保證計算結果的準確性，取仿真次數n為106。

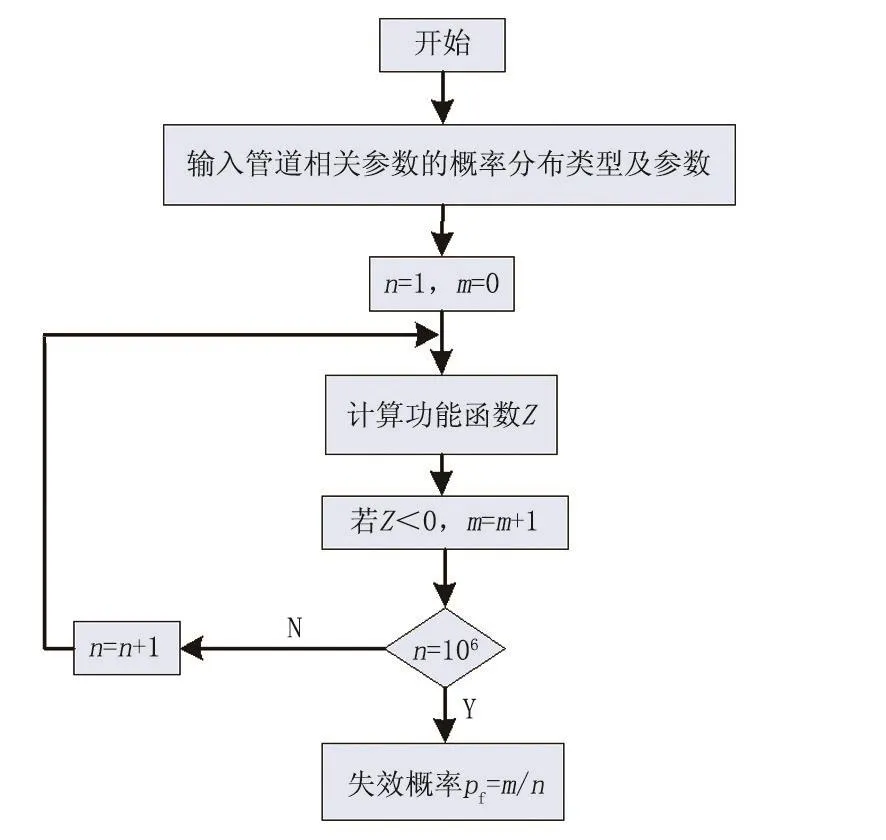
圖1 Mont e-Car l o法計算流程圖Fig.1 Calculation flow chart of Monte-Carlo method

2 實例計算

根據參考文獻[5]，管道的基本參數如表1、表2所示。

表1 管道尺寸Tab.1 Pipe dimensions

表2 管道運行壓力Tab.2 Pipeline operating pressure

2.1 目標可靠度

本文采用基于可靠性理論的分析方法來評估腐蝕管線。為此，以API 579—2007提出的管道目標可靠度為依據，其中一類地區對應低風險，二類地區對應中風險，三、四類地區對應高風險（表3）[6]。受干擾較大的管道一般處于高風險地區，所以下文取0.999 99為管道目標可靠度。

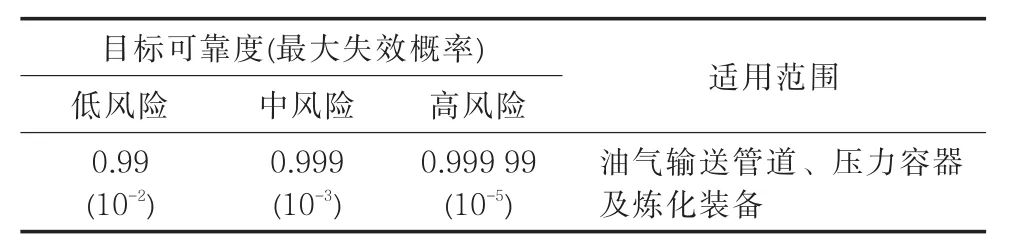
表3 目標可靠度Tab.3 Target reliability

2.2 可靠度計算

取腐蝕缺陷平均長度為管道外徑的一半，變異系數為0.1；取缺陷深度分別為壁厚的10%、20%、30%、40%、50%，變異系數為0.1。采用基于B31G的Monte-Carlo法計算管徑為1 219 mm的X80管道的可靠度。計算結果（表4）表明，當腐蝕深度小于管道壁厚的30%時，可靠度都遠高于0.999 99，隨著腐蝕深度的加深，當深度大于管道壁厚的40%時管道運行時的可靠度小于目標可靠度0.999 99。所以當腐蝕深度大于管道壁厚的40%時應當采取相應的安全措施，如更換新的輸氣管道或者降低當前的運行壓力。

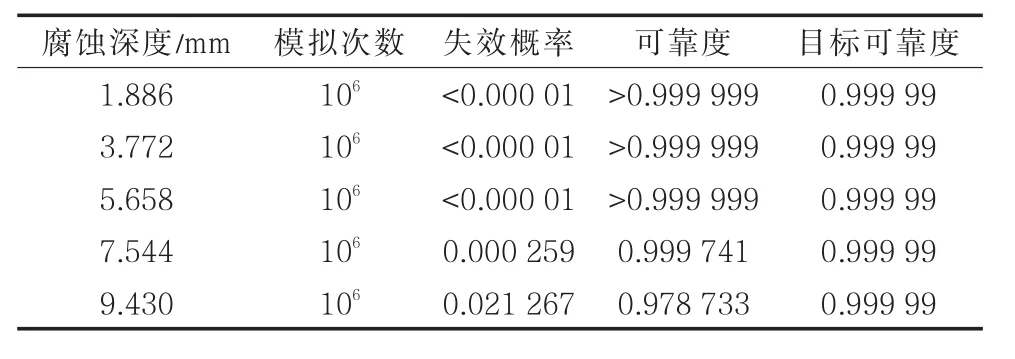
表4 可靠度計算結果Tab.4 Reliability calculation results

2.3 敏感性分析

對于有腐蝕缺陷的輸氣管道，管道的不確定參數包括管道外徑、管道壁厚、拉伸強度和管道內壓、缺陷長度和缺陷深度，分別取參數標準差的50%、100%、150%、200%、250%、300%對管道進行可靠度分析，為保證結果的精確性，每次模擬次數為106。結果如圖2所示，控制各隨機管道參數變異系數不變，當增大管道壁厚、拉伸強度、管道外徑、管道內壓、缺陷長度和缺陷深度六個參數中一個參數的變異系數之后，管道的可靠度有所降低。其中對管道可靠度影響最大的是缺陷深度，其次是管道內壓和管道壁厚。

圖2 參數標準差變化對可靠度的影響Fig.2 Influence of the variation of parameters standard deviation on reliability

3 結束語

地鐵及高壓直流輸電系統在運行時會對管道產生雜散電流干擾，電流的流出端會加速管道的腐蝕。以西氣東輸二線所用的X80管道為算例，基于B31G標準對含有腐蝕缺陷的管道建立了可靠性模型，將各不確定的輸氣管道參數帶入到極限狀態方程中，由于計算難度較大，采用了Monte-Carlo法來獲得可靠度結果。經過分析得到當腐蝕深度大于管道壁厚的40%時，管道可靠度計算結果小于目標可靠度，應采取相應的安全措施，如更換新的輸氣管道或者降低當前的運行壓力。對各個參數進行敏感性分析表明，對管道可靠度影響最大的是缺陷深度，其次是管道內壓，所以在管道運行期間應當主要關注管道的腐蝕程度以及管道壓力的變化。