一種變徑減阻的方法★

陳永健 馮仁杰 程鵬月 劉 錦 趙 琦

(河北建筑工程學院，河北 張家口 075000)

管道內的流體，由于流體流經變徑結構時會產生局部阻力損失，這是因為流動邊界條件改變，而流體沒有及時的改變，會產生一定的旋渦，由于旋渦的產生會造成局部阻力損失[1]，本文在最小作用量原理基礎上，提出了一種減小局部阻力損失的方法即通過找到流體流經減阻結構時的流線方程，改變流體的外部邊界形狀，使得邊界形狀與流體流線最大限度重合，減小流體流經變徑的局部阻力損失，如何根據最小作用量原理找到流體流經變徑結構的流線方程，是本文的重點。

1 最小作用量原理的一般表述

自然界中各種類型的宏觀現象(例如：力學、熱學、光學、電磁學等現象)[2]在一切實際現象的發生過程中，始終滿足:

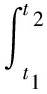
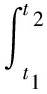
最小作用量原理有兩個層次的應用，第一個層次就是描述物理過程基本規律的原理，即一般用變分的形式將偏微分方程形式的規律統一起來；第二個層次則是根據基本規律用來實現對實際物理過程優化設計和控制。

2 減阻方法的提出

最小作用量原理現在已經成為物理學研究方法中的最基本的方法，也是科學家研究宇宙問題時最簡單明了的基本準則，更是描述客觀事物規律的一種方法[3]。即認為所有的動力學體系均可以用作用量方式來描述，通過作用量取極值來確定。認為作用量最小的那個，是物體的實際運動。而在費曼路徑積分方法中，認為粒子每一條路徑的權重其實是這條路徑的作用量所決定的，但這是量子體系的描述，不能說體系中挑選了某一條最近的路徑，而是所有的路徑都對動力學作了貢獻。我們不用考慮是否是作用量最小，只知道在作用量取得極值時，就代表了物體實際的運動過程[4]。

最小作用量原理反映了事物的變化在運動路徑上所遵循的規律。由于最小作用量原理的簡單和普遍適用特性，我們在應用最小作用量原理的思想研究流體質點通過變徑問題時，通過使用最小作用量方法來觀察流體質點所走的路徑，并找到流體質點運動的真實路徑而不是其他的路徑。我們不僅要考慮流體質點從A到B可能走的所有路徑，而且還要考慮它走這一段路程的所有可能的形式。我們可以把在一定時間內流體質點走過這一路徑的每一種特定形式定義為一個“經歷”。通過定義相關作用量變化的函數，然后算出一給定流體質點在任一經歷下的作用量，我們就完全掌握住了這個物體的運動情況。當我們找到變徑時的作用量函數時，根據最小作用量原理可以知道，它不同于一般泛函數(簡單的說，泛函的定義域是函數集，值域是數集，即泛函是從函數空間到數域的一個映射)取最值原理，我們按照費曼的解讀可以知道，最小作用量原理不要求泛函數取得最大值或者最小值，甚至不需要取得極大值或極小值，僅僅取得駐值就有可能代表了真實的物理過程。也就是說當此函數取極值時，我們就可以確定流體流過變徑區域的真實運動軌跡，然后通過改變固體邊界保證流體流動軌跡與固體邊界完全重合時，或者盡最大可能重合時，使得流體流過變徑區域既沒有碰擊，又無因脫離而產生的附加能量損失，從而使得流體通過變徑區域的阻力最小。這即是通過最小作用量原理提出減阻方法的核心思想。

在研究流體變徑問題時，只需要找到作用量方程即拉格朗日函數，而無需參照特別的坐標系，這是我們通常使用牛頓定律研究力學所不具有的。它表現形式更加簡單，幾乎一個簡潔的的公式就可以求解所有的力學量。盡管和牛頓運動定律表現形式不同，但是它們之間是等價的。

3 定義作用量函數

我們可以知道，理想不可壓縮流體恒定流元流能量方程為:

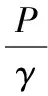
我們把前兩項相加，以Hp表示：

其中，Hp為元流斷面測壓管水面相對于基準面的高度，稱為測壓管水頭，表明單位重量的流體具有的勢能稱為單位勢能。

三項相加，以H表示：

其中，H為總水頭，表明單位重量的流體具有的總能量，稱為單位總能量。

根據元流能量方程式，我們可以知道理想不可壓縮流體恒定元流中，各斷面總水頭相等，單位重量的總能量保持不變。元流能量方程式，確立了在一元流動中的動能和勢能，也確立了流速和壓強相互轉換的普遍規律。在流體變徑過程中我們只考慮動能和壓能的相互轉化關系，為此我們可以根據元流能量方程式定義作用量的表達式方程。

定義拉格朗日函數：

定義時間的函數：

l(t)=t。

作用量為：

其中，δS為S的變分，我們可以知道只要使得：

δS=0。

我們即可求解出流體從A點到B點的真實路徑，即流體從A點到B點的真實路徑軌跡。

4 求解拉格朗日微分方程

已知條件:

xt1=xA。

xt2=xB。

即流體每條路徑都是從t1時刻從A點出發，在t2時刻到達B點，這些地點和時間都保持不變,如圖1所示。

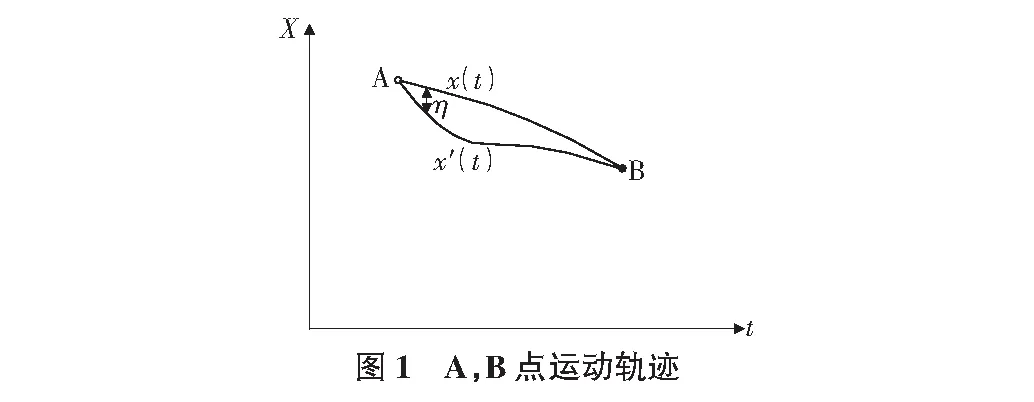
為了進一步解析方程我們可以設定幾個參數：

1)流體從A點流動到B點的任意路徑是x′(t)，作用量是S′。

2)流體從A點到B點的真實路徑x(t)，作用量是S。

3)任意路徑與真實路徑的偏移量η(t)=x′(t)-x(t)表示任意路徑與真實路徑的微小差別。

在此基礎上對其進行求解，只要使得在偏移量η的第一次近似上應等于0:

η(t1)=0,η(t2)=0。

我們把參數帶入作用量公式可得：

那么通過真實路徑對此進行表示作用量把:

x′(t)=η(t)+x(t)。

代入該作用量公式進行替換那么我們可以得到這樣的一個表達式：

通過對其平方項進行展開，我們可以得到：

對于最小偏移量η的二次項忽略不計，因此動能的部分我們可以得到這樣的一個表達式：

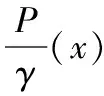
對于二階和更高階η，忽略不計那么S為:

我們現在的問題是雖然我們不知道x(t)是什么，但是我們知道不管η是什么，但是我們知道δS=0，這一積分為總是為0，我們只要保證δS=0，即是得到最終曲線。

通過分部積分法可得：

由于η(t1)=0，η(t2)=0。積分結果為0。

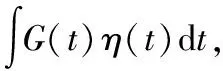
據此我們得到了在流體通過變徑過程中的微分方程，只有對于滿足這微分方程的路線，也就是流體通過變徑時候的真實路徑。然后通過初始條件我們可以求出質點的運動軌跡。

5 結語

本文在流體中應用最小作用量原理思想提出了變徑減阻的方法，介紹了最小作用量原理一般表述和應用方法，最小作用量原理思想雖然和物理學中牛頓定律表現形式不同但是它們是等價的，最小作用原理比牛頓第二定律更加方便，最小作用量原理把尋找拉格朗日量作為出發點，推導出質點運動軌跡滿足的微分方程，因此我們可以通過最小作用量原理推導出流體變徑時流體的真實的運動軌跡，由于流體動力學研究的主要問題是流速和壓強在空間的分布，本次針對流體變徑中流線的分布，通過簡化物理模型，不同于以往用歐拉法來研究流體的流場而是應用于用拉格朗日法來描述質點的運動找到流體變徑時的真實路徑。流體變徑時主要是壓能和動能之間的相互轉化，為了應用最小作用量原理思想到找到流體變徑時候的流體軌跡方程，把壓能和動能轉化關系定義為作用量函數然后對其進行求駐值，從而確定流動的微分方程式，通過初始條件我們可以知道流體變徑時，流體真實的路徑，通過對流體進行進一步的分析，確定了減阻結構的形狀，這樣我們為流體通過變徑結構時提供了理論基礎也為以后的變徑結構提供了設計依據。