稍不均勻電場中低氣壓擊穿的起始路徑研究*

于博 梁偉 焦蛟 康小錄 趙青 ?

1) (電子科技大學, 信息地學研究中心, 成都 611731)

2) (上海空間推進研究所, 上海 201112)

1 引 言

本文研究所提到的稍不均勻電場的間隙是指電場不均勻系數f在2.0–4.0 (f為電場中最大場強與平均場強的比值)的電極間隙. 在低壓氣體擊穿的研究中, f在2.0–4.0的電極是較為常見的工程研究對象, 主要涉及真空環境下的氣體放電觸發以及電極表面的削蝕等問題. 近年來, 尤其在空間電推進領域, 推進系統的點火性能設計常涉及到非勻強電場的低壓擊穿問題, 多次氣體放電工況中的電極表面打火點是目前比較受關注的研究方向.

根據經典帕邢定律[1], 在無限大的兩平行電極間, 臨界擊穿電壓(能夠引發擊穿的電壓下限, 下文均簡稱擊穿電壓)與電極間距d和間隙壓強p的乘積有關, 其擊穿電壓曲線呈現為“U”型. 在此類工況中, 電極間的電場分布、壓強分布都均勻, 間隙距離處處相等, 那么在擊穿間隙的所有區域都會發生電子雪崩, 這種擊穿過程可認為是一種全通道的放電過程. 然而, 在非勻強電場電極的工況中,擊穿放電并非全通道放電. Golden等[2,3]首先發現非勻強電場電極下的擊穿電壓與湯森放電模型的預估值不一致, 認為湯森電離系數在描述非勻強電場的電離次數時, 在不同間隙位置的描述方式會存在差異, 所以對湯森第一電離系數做出了修正, 得到了與試驗較吻合的結果, 這是首次發現非勻強電場工況與全通道放電工況的機制不同. 接著,Osmokrovic等[4,5]針對幾種典型復雜電極進行了擊穿電壓的測量試驗, 通過分析試驗結果, 發現復雜電極間的擊穿總會存在一個“臨界區域”, 該區域會首先觸發擊穿, 接著擊穿過程將快速蔓延至整個放電通道, 但在他的研究中僅說明這種“臨界區域”會隨著壓強、電極結構的不同而改變, 沒有揭示如何確定這種“臨界區域”的具體位置, 并且相關的物理機制尚不清晰. 然而, 對于非勻強電場的電極來說, 獲得“臨界區域”的位置對于預估擊穿電壓以及研究電極點火的主要削蝕點均有著重要意義. 鑒于試驗方法具有一定局限性, 因此, 本文將采用數值與試驗結合的方法來對“臨界區域”(本文稱之為起始擊穿路徑)進行研究.

到目前為止, 關于低氣壓放電路徑的數值研究鮮有報道, 所以本文將從高氣壓放電路徑的研究來獲得一些借鑒與啟發. 由于高氣壓下的放電路徑在大量統計數據中既具備一定的自相似性, 又會在流注傳導時表現出一定的隨機性. 于是, 根據這種客觀物理規律, Niemeyer 等[6]建立了經典的流注分形模型, 主要實現流注頂端的電場強度能否維持放電持續的判斷以及放電發展方向的隨機判斷. 接著, 如果考慮放電初始電場與放電中的電勢降, 則需要修改電場強度的求解模型[7]. 在此基礎上,Niemeyer[8]又提出先導的隨機漫步模型, 通過在拉普拉斯背景電場中建立線性曲線坐標系來實現多條潛在先導路徑的劃分, 并計算了當地先導的擴散度, 進而求解了當地先導的擴散概率方程以實現放電路徑的模擬, 所得計算結果的圖像就像先導在無數階梯中進行隨機漫步一樣. 但在實際情況中, 放電通道的電介質不都是均勻分布的, 因而還需要考慮將電導率、介電常數進行空間函數化處理, 以修正空間各位置的放電擴散概率[9]. 隨后的研究, 主要表現為對擴散概率、分形維度等經驗參數的修正[10?12].

實際上, 高氣壓的流注模型與低氣壓的電子雪崩模型有本質區別, 分形理論并不能適用于低氣壓的放電路徑模擬. 但是, 通過對流注分形模型的認知, 可以確定低氣壓放電路徑模擬需要2個關鍵條件： 第一, 模型應具備對放電維持的判斷; 第二, 模型應具備對潛在放電路徑的劃分, 并且這種劃分要符合客觀規律(高氣壓的放電路徑具有隨機性, 故流注模型利用概率判斷的擴散分形方法就非常符合客觀規律). 因此, 本文在建立低氣壓放電的起始路徑模型時將充分考慮這2個條件.

首先, 根據湯森放電理論, 電子雪崩放電過程的維持必須要有電離碰撞作為先決條件[13], 由此,應引入模擬電離碰撞等相關的碰撞概率模型, 在以往的等離子體放電研究中, 蒙特卡羅模型是比較成熟的碰撞概率判斷模型, 該模型曾應用于強電場間隙的逃逸電子流模擬[14,15]、小間隙的擊穿放電模擬[16], 獲得了計算結果與試驗結果較高的吻合度.其次, 低氣壓下的背景氣體數密度較低, 這使得電子與背景氣體發生彈性碰撞散射的概率較低. 同時, 電子運動受電場力約束較顯著, 在擊穿過程中即使發生散射也會再漂移到附近區域的電場線中,從統計學角度來看, 這類似于一群電子沿著相鄰幾條電場線遷移. 因此, 本文采用“電子沿電場線”的運動假設, 認為潛在的擊穿起始路徑由若干條電場線組成, 且該假設在 Macheret和Shneider[17]的“非散射傳導”(forward?back)模型中也有體現. 結合上述2個條件, 我們建立一種基于電場線路徑假設、蒙特卡羅碰撞模型的起始路徑判斷模型(determination of the critical path, DCP模型).接著, 為驗證DCP模型的計算精度, 開展2種電極結構的擊穿放電試驗, 以說明DCP模型的有效性. 在此基礎上, 將DCP模型應用于其他4種有代表性結構的電極計算中, 獲得稍不均勻電場下低氣壓擊穿起始路徑的位置規律和相關物理內涵.

2 數值模型

為實現稍不均勻電場間的起始路徑預估, 我們建立起DCP模型. 此模型的建立思想為： 在電極間隙中尋找一條最可能發生擊穿的起始路徑, 若該路徑剛好可以觸發局部擊穿過程, 則整個間隙將完成臨界擊穿.

DCP模型的整體計算流程如下：

Step.1 基于“電場線為電子運動軌跡”假設, 在電極間劃分若干條候選擊穿路徑(可能成為起始擊穿路徑的路徑);

Step.2 設定電極間的電壓差(電極電壓U0),并將劃分好的候選擊穿路徑以等電勢線正交分割開來, 以路徑線和等勢線的交點為計算節點;

Step.3 在負電極表面的每一個計算節點設定相等數量(n0)的初始電子, 這些初始電子在電極電壓的作用下會沿著各自的候選路徑向正電極運動, 沿程計算電子動能變化、各類碰撞概率;

Step.4 統計每一條候選路徑所發生的總電離次數以及所產生的正離子數量, 并計算這些正離子撞擊負電極表面所產生的二次電子數量(nγ);

Step.5 篩選所有候選路徑中nγ最多的一條記為起始擊穿路徑, 并判斷這條起始路徑的nγ,max與n0之間的關系. 若nγ,max明顯低于n0, 則無法實現擊穿, 適當升高電極電壓(更新Step.2中的U0, 繼續迭代計算); 若nγ,max明顯高于n0, 則觸發“過量擊穿”, 適當降低電極電壓(更新Step.2中的U0, 繼續迭代計算); 若滿足 nγ,max接近n0, 則剛好實現臨界擊穿(計算收斂).

具體物理模型細節將于下文詳細介紹.

2.1 計算節點劃分

首先, 進行間隙中候選擊穿路徑的劃分. 假定在負電極表面存在一些均勻分布的初始電子, 以這些電子來代表間隙中由宇宙射線等外界因素所觸發的原始電子. 這些負電極表面的電子將會沿著各自的候選路徑, 在電極電壓(U0)的作用下運動到正電極表面. 這里, 由于低氣壓湯森放電中的空間電荷效應不顯著, 忽略空間凈電荷分布對電場的影響. 那么, 如果假設電子的運動路徑為電場線, 則這些負電極表面均布的電子會通過均勻劃分的候選路徑向正電極運動(圖1).

圖1 典型非平行電極間的計算節點劃分示意圖Fig. 1. Schematic diagram of the mesh grid generation in nonparallel two?electrode gap.

接著, 以若干電位等勢線來分割候選路徑, 使得所分割的微元路徑上的電勢降都相等. 于是, 整個間隙中由等勢線和候選路徑形成的交點, 就是計算節點.

2.2 電子動能及碰撞概率

假設每一條候選路徑從負電極表面都會觸發n0個初始電子向正電極運動. 這些電子會在電極電壓(U0)的作用下增加動能, 并觸發與背景中性氣體的碰撞過程.

根據2.1小節的闡述, 電子在任意候選路徑上運動時, 每經過一個微元路徑, 將會降低相同的電勢能(), 而動能將增加(e為元電荷,那么, 當電子具有一定動能時, 必將觸發與中性氣體的碰撞.

根據蒙特卡羅碰撞(Monte?Carlo collisions,MCC)模型, 一個電子在中性氣體中, 在極短時間內的碰撞概率為

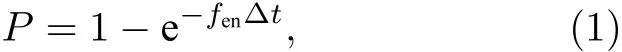
第二種, 如果間隙壓強分布不均勻(通常由氣體流動產生), 則需要通過求解數密度分布場來獲得某一網格節點下的數密度分布數據, 但是, 求解數密度的網格節點與DCP模型的計算節點劃分一般不同, 所以還需要利用插值(通常采用權重法)來獲得DCP計算節點的. 圖2給出了典型空心陰極的氣體流動間隙中的計算方法.

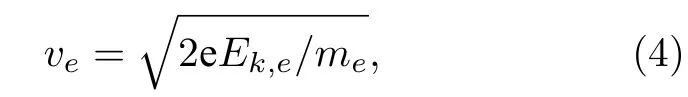
圖2 間隙壓強不均布時的 計算方法Fig. 2. Computational method of the in the gap of non?uniform pressure distribution.

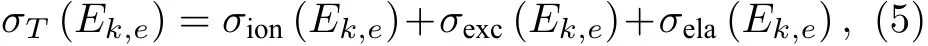
其中, 下角標“ion”代表電離, “exc”為激發, “ela”為彈性. 最后, (1)式中的可以由(6)式計算：

(7)式描述的是電子與中性氣體的總碰撞概率, 但對于電子動能損耗而言, 只有電離碰撞和激發碰撞是影響電子動能的關鍵碰撞類型. 因而, 本文主要考慮上述二者的碰撞概率, 有

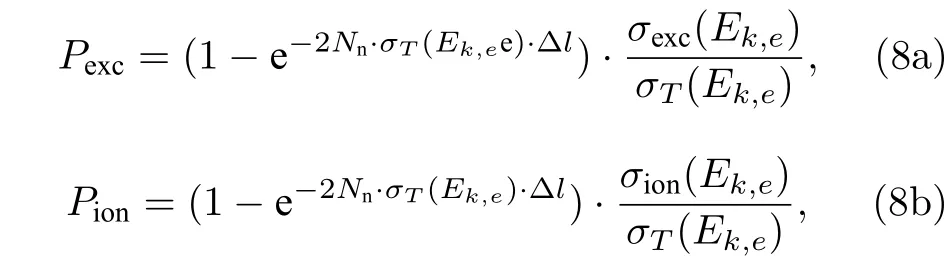
在電子與Xe原子發生電離或激發碰撞后, 動能會降低相對應的電離能級(12.1 eV)或激發能級(8.4 eV).

2.3 起始擊穿路徑判斷

在每一條候選擊穿路徑中, 會由于高能電子觸發的電離碰撞而產生大量的正離子, 這些正離子會在電極電壓的作用下向負電極移動; 同樣地, 由于離子?中性粒子的碰撞頻率遠小于電子?中性粒子(這里忽略離子的散射運動機制). 當離子到達負電極表面時, 會產生二次電子發射, 根據文獻[19], 低能離子轟擊不銹鋼表面(后文所有工況均采用不銹鋼為負電極)所產生的二次電子發射系數在0.021–0.023, 本文取0.022. 那么, 當某條候選路徑在n0個初始電子的觸發下產生nion個正離子時,這些正離子轟擊在負電極面所產生的二次電子可描述為

表1 e?Xe的碰撞截面公式[18]Table 1. The e?Xe collision cross?section[18].

接著, 統計每一條候選擊穿路徑的nγ, 選取產生二次電子最多的一條為起始擊穿路徑, 因為這條路徑最具備觸發局部擊穿的可能. 于是, 判斷這條路徑的二次電子數量nγ,max與初始電子數量n0的大小關系：

這里, c0為計算收斂的相對殘差, 是一個趨近于0的正實數. 如果c0取0.001, 則表示由殘差所約束的計算誤差不會超過0.1%, 該數值越小, 計算精度越高; 但同樣地, 迭代次數也會越多, 收斂速度越慢. 在本文的工況中, 綜合考慮計算精度與速度, 取 c0= 1 × 10–4.

在第二或第三情況中, 本文給出調整電極電壓U0的一個較為簡單的迭代公式為

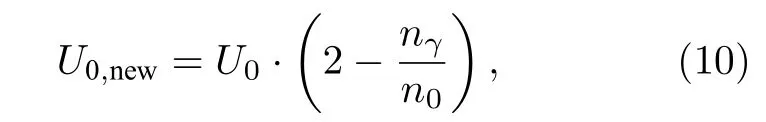
2.4 影響模型誤差的參數

在DCP模型中, 除收斂參數c0外, 還有2個參數會影響模型的固有誤差： 每條候選路徑上的初始電子數量n0和微元路徑上的電勢降.

n0主要影響碰撞概率判斷所調用的樣本空間大小, n0越大, 由MCC模型所計算的結果與實際結果偏差越小. 圖3給出了重復多次計算后, case1(見第3節)中No.21候選路徑的平均每個初始電子所產生的總電離次數的結果波動情況. 在一個比較極端的情況(n0= 1)中, 結果波動非常明顯, 這說明較少數量的初始電子會導致計算結果的隨機性較高; 而當n0= 200時, 計算結果的波動已經非常微弱, 即使在n0= 500時, 這種波動的改善也不會太多. 這意味著, 這種波動誤差無法根除, 但可以控制在某個范圍內. 考慮n0對計算結果波動和計算時間的影響, 取n0= 200比較合理, 可以將結果的波動控制在0.5%以內. 值得注意的是, 圖3所展示的是MCC模型在計算中產生的不穩定性隨n0的依變關系, 具有一定的普適性, n0= 200對于其他工況而言也同樣適用.

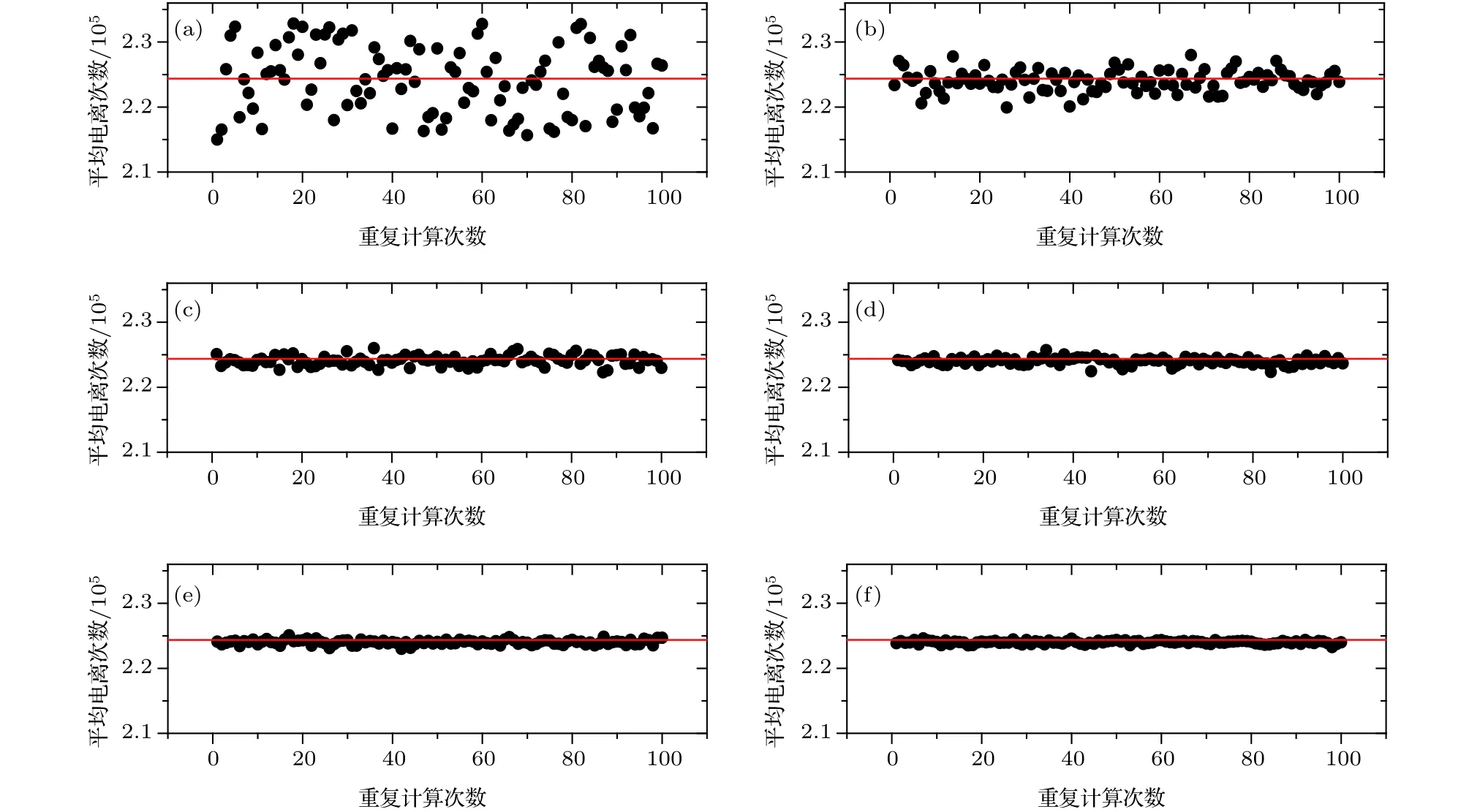
圖3 DCP計算結果穩定性隨N0的依變關系(a) n0 = 1; (b) n0 = 10; (c) n0 = 50; (d) n0 = 100; (e) n0 = 200; (f) n0 = 500 (case 1, 間隙壓強60 Pa, 臨界擊穿電壓345 V)Fig. 3. The computational stability of DCP model as a function of N0： (a) n0 = 1; (b) n0 = 10; (c) n0 = 50; (d) n0 = 100; (e) n0 =200; (f) n0 = 500 (An example of case 1, gap pressure： 60 Pa, critical breakdown voltage： 345 V ).

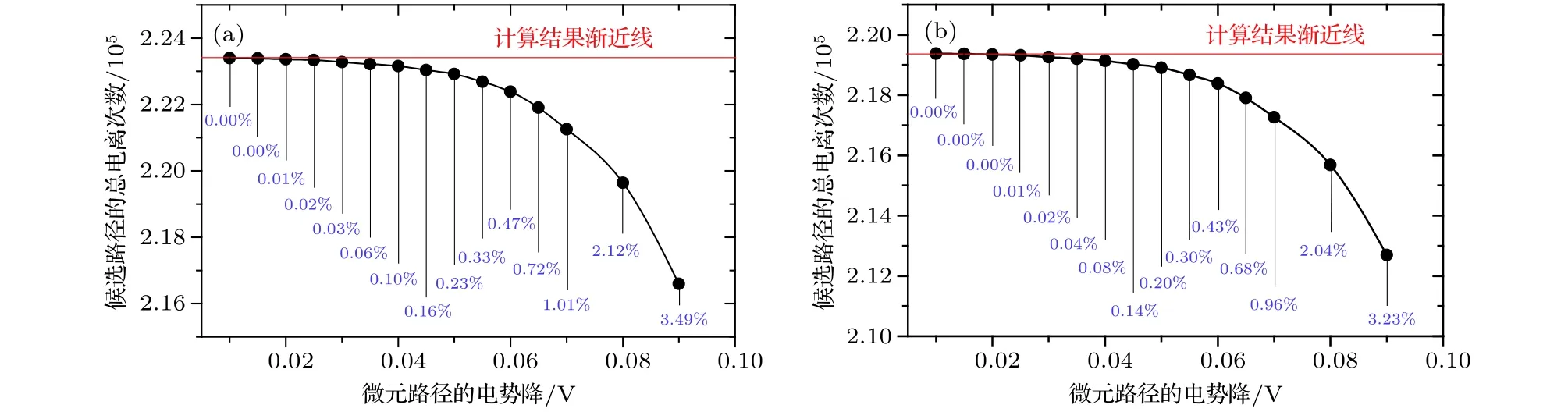
圖4 路徑總電離次數的計算值隨 變化的偏差 (a) No.1候選路徑; (b) No.21候選路徑Fig. 4. The computational deviation of total ionization number in one path at different ： (a) Potential path of No.1; (b) poten?tial path of No.21.

本文限定的電場不均勻系數f也是有關模型誤差的參數. 如果局部電場強度過高, 會導致電子運動到弱場強區域時, 脫離電場線軌跡. 因而, 關于f取值應該有上限值, 但本文所采用的驗證試驗工況只能覆蓋f ≤ 3.97范圍, 故將本文研究的電極范圍限定在2.0–4.0. 此外, 背景壓強對于“電子沿電場線運動”的假設有支撐作用, 當壓強升高到一定程度時, 電子的流注特性會逐漸升高, DCP模型同樣會失效, 根據驗證試驗結果, DCP模型在壓強低于103Pa量級時能夠保證較高精度.

3 模型驗證

前文有述, DCP模型可以計算2個物理參數：起始路徑和擊穿電壓. 那么, 本節將開展驗證試驗,從這2個方面來對DCP模型進行驗證.

3.1 試驗系統及測量方法

如圖5所示, 整個試驗在0.6 m(直徑)× 2 m(長度)的真空艙內進行, 抽氣系統由機械泵(負責粗抽)和分子泵(負責精抽)組成, 艙內壓強范圍可以控制在5 × 10–3Pa到5000 Pa之間, 滿足試驗需要. 電極裝置固定在圖5中黑色虛線區域, 由于試驗所用電極裝置不止一個, 所以這里沒有展示具體電極結構. 當擊穿工況屬于均勻壓強分布時(如case 1), 采用流量通道2, 將氣體工質快速分散到艙內, 并以玻璃罩來覆蓋住電極裝置區域, 以減少由于艙內氣體流動導致的試驗誤差. 當擊穿工況屬于非均勻壓強分布時(有氣體來流的電極, 如case 2), 則采用流量通道1, 將氣體工質通入電極內部,并且不使用玻璃罩.

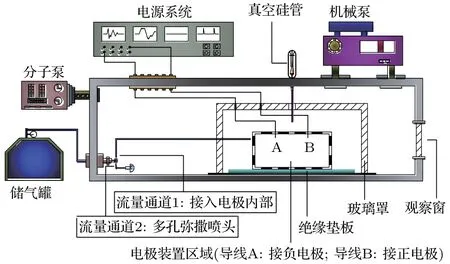
圖5 擊穿試驗系統布置Fig. 5. A diagram of the test layout.

接著, 對起始擊穿路徑和擊穿電壓的測量方案進行討論. 擊穿電壓的測量可以通過具有波形采集功能的電源系統來進行, 而起始擊穿路徑的測量就具有一定難度. 起初, 有2個方案進入考慮范圍：(1)通過高速相機對電極間的放電閃光位置進行瞬間捕捉拍照; (2)通過多次循環試驗考察負電極表面的離子轟擊痕跡. 但是, 經過深入思考, 方案(1)存在一定的疑問： 放電閃光是由激發態原子退激所輻射的光子組成, 具有放電閃光的位置可以直接說明該位置最先產生激發碰撞, 但不能直接證明該路徑就是電子雪崩過程最劇烈的路徑, 即無法證明該路徑就是起始擊穿路徑. 因此, 本文將采用方案(2)來測量起始擊穿路徑位置. 如果對整個放電過程進行合理的控制, 就可以在電極間制造只有起始路徑發生擊穿的放電過程. 那么, 在負電極表面所形成的正離子轟擊痕跡, 就能夠指向起始路徑的位置. 由此, 方案(2)需要先認知放電過程的電壓電流的時間特性曲線 (VI?t曲線), 典型的 VI?t曲線如圖6所示.

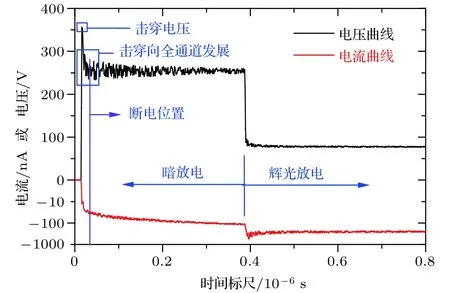
圖6 放電過程的VI?t曲線(數據來自case 1工況)Fig. 6. VI?t curve of the discharge process in case 1.

圖6 中電壓曲線的最高點就是起始擊穿路徑剛好發生擊穿的時刻, 而采集到的電壓數值就是擊穿電壓. 在起始路徑的擊穿剛觸發后的0.05內,擊穿電壓會迅速下降, 并伴隨電流的迅速上升, 這一段就是由起始路徑局部擊穿向全通道過渡的階段, 因為放電路徑的增多必然伴隨電流升高, 因此,只要在局部擊穿完成后關閉電源, 就可以將電極間的放電嚴格控制在只有起始擊穿路徑擊穿的階段.根據多次VI?t曲線的采集結果, 發現恰好進入暗放電的擊穿電流(絕對值, 下同)在100 nA量級,而湯森擊穿剛好發生時的擊穿電流在10 nA量級,這說明應該將斷電條件設定為“當擊穿電流大于10 nA 時, 斷開電源輸入”. 然而, “10 nA”的數值太小, 以致放電時間不充足, 在103次量級的循環擊穿試驗中, 負電極表面很難形成明顯痕跡, 因此,經過多次調試, 如果斷電條件中的擊穿電流在50 nA時, 可以在103次量級的循環擊穿中對負電極表面留下較清晰的痕跡, 并且這些痕跡具有較高的指向性.

3.2 仿真與試驗結果對比

本文選取2種電極裝置來驗證DCP模型的計算精度： 圓片階梯電極(case1)和磁等離子體動力學推力器(magneto?plasma dynamic thruster, MPDT,case2).

3.2.1 Case 1

Case 1為圓片階梯電極, 結構尺寸與候選路徑劃分見圖7. 這里, 給出電場系數f, 以表征電極電場的不均勻程度(后文均有標注). 負電極表面的削蝕痕跡見圖8(a), 擊穿電壓?間隙壓強(V?p)曲線以及起始擊穿路徑的計算結果見圖8(b).

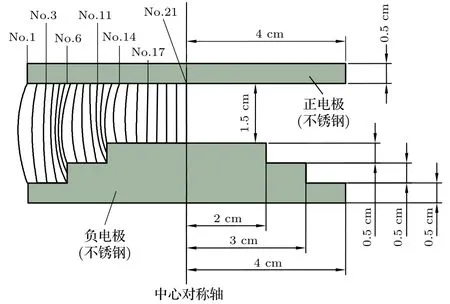
圖7 圓片階梯電極的結構及候選路徑劃分(f = 3.97)Fig. 7. The geometry and potential path generation in the laddered plate electrode (f = 3.97).

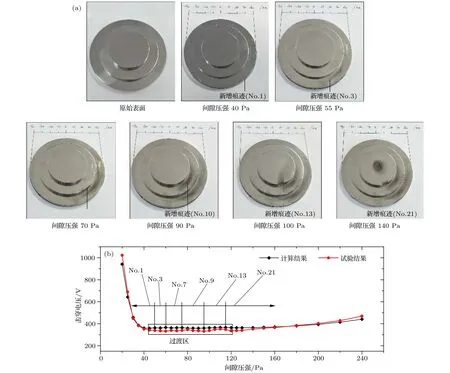
圖8 Case 1試驗與計算結果對比(氣體工質： Xe)Fig. 8. The comparison of the calculation and test results in case 1 (working medium： Xe).

根據圖8(a), 這里進行2點關于試驗現象的說明： 第一, 由于不銹鋼電極含C元素, 在負電極表面削蝕過程中會產生一定的C原子沉積, 因此電極表面某些位置會有黑色痕跡(而case 2的負電極為W, 所以并沒有這種黑色痕跡); 第二, 由于電極加工精度以及兩電極安裝的平行度難以達到絕對標準, 所以原本應在回轉體電極一周都出現的削蝕痕跡, 只出現在某些局部位置, 但這些位置依然可以指向起始擊穿路徑. 根據試驗結果, 我們發現負電極表面的新增痕跡趨勢會隨著間隙壓強的變化而變化, 與Osmokrovic描述的臨界區域變化的現象基本相符. 并且, 雖然電極表面痕跡所指向的起始路徑與計算結果不完全一一對應, 但所呈現的路徑轉移趨勢與計算結果可以保持定性一致. 在擊穿電壓的計算方面(圖8(b)), DCP在case1的計算相對誤差在0.56%–5.88%, 尤其在起始擊穿路徑轉移的過渡區, 可基本捕捉擊穿電壓的變化趨勢.

3.2.2 Case 2

Case 2為MPDT的擊穿工況, MPDT屬于電推進動力裝置, 本文的MPDT采用20 kW級、推力為600 mN的原理樣機, 該樣機的應用平臺為高軌XX衛星的軌道轉移推進系統. MPDT的點火過程起始于陰極管與陽極環之間的擊穿, 當放電足以令鎢陰極管達到熱發射溫度時, MPDT則迅速進入穩定工作狀態. 推力器的電極結構和候選路徑劃分見圖9, 負電極(陰極管)表面的痕跡結果及擊穿電壓?氣體流率(V?fr)曲線見圖10. 其中, 氣體工質為Ar, 關于Ar的碰撞截面公式見文獻[20],Ar與其它材料負電極的二次電子發射系數見文獻[21].

據圖10, 同樣地, 負電極表面的新增痕跡趨勢與起始路徑計算結果的趨勢在定性層面保持一致,并且, 擊穿電壓的計算相對誤差在0.42%–7.90%.

綜上, 通過試驗與計算結果的對比, 可以初步證實： 第一, 起始擊穿路徑確實會發生轉移; 第二,DCP模型能夠從定性角度捕捉起始擊穿路徑的轉移方向.

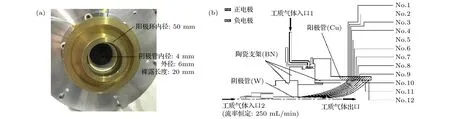
圖9 MPDT電極的相關信息 (a)實物照片; (b)電極結構及候選路徑劃分(f = 2.47)Fig. 9. The relevant information of the MPDT： (a) Physical photograph; (b) the electrode geometry and potential path generation.

圖10 Case 2試驗與計算結果對比(氣體工質： Ar)Fig. 10. The comparison of the calculation and test results in case 2 (working medium： Ar).

4 計算結果

前文對DCP模型的計算精度進行了初步驗證, 并通過case 1和case 2的結果展示出起始擊穿路徑的相關特性. 為進一步研究起始路徑的這種特性, 本節將給出其他4種比較有代表性的電極結構, 以歸納出起始路徑轉移的普遍規律.

4.1 case 3

Case 3為兩非平行直板電極間的擊穿工況,如圖11(a)所示, 電極在入紙面方面為無限長, 兩電極結構完全相同, 計算結果見圖11(b).

4.2 Case 4

圖11 Case 3的計算輸入條件及計算結果(氣體工質： Xe) (a)電極結構及候選路徑劃分(f = 2.45); (b)V?p曲線的計算結果及起始路徑分布Fig. 11. The input conditions and calculation results in case 3 (working medium： Xe)： (a) The electrode geometry and potential path generation; (b) the calculation results of the V?p curve and the critical path distribution.

圖12 Case 4的計算輸入條件及計算結果(氣體工質： Xe) (a)電極結構及候選路徑劃分(f = 3.76); (b)V?fr曲線的計算結果及起始路徑分布Fig. 12. The input conditions and calculation results in case 4(working medium： Xe)： (a) The electrode geometry and potential path generation; (b) the calculation results of the V?p curve and the critical path distribution.

Case 4為無加熱器空心陰極(heaterless hollow cathode, HHC)的工況. 在HHC點火過程中, 陰極管?觸持極間會首先引發氣體擊穿, 通過離子轟擊負電極表面而加熱發射體, 使發射體達到工作溫度(1300 K左右), 然后在陰極管?陽極板間進行穩定放電(陽極板在觸持極右側2–3 cm, 圖12(a)未展示). 因此, HHC的點火性能主要依賴于氣體擊穿過程. HHC擊穿所發生的正負電極結構見圖12(a), 計算結果見圖12(b).

4.3 case 5

Case 5為兩平行圓柱電極間的擊穿工況, 電極在入紙面方面為無限長, 2個電極結構完全相同(圖13(a)), 計算結果如圖13(b). 氣體工質為Ar.

4.4 case 6

Case 6為圓柱?直板電極間的擊穿工況, 兩電極在入紙面方向無限長, 并且, 兩電極的中心軸線平行. 電極結構及候選路徑劃分見圖14(a), 計算結果見圖14(b). 氣體工質為Xe.

綜上, 通過對case 1到case 6的對比分析, 發現這6個工況的計算或試驗結果都存在一些共有的特性：

(1)在壓強或氣體流率上升過程中, 起始擊穿路徑并不是固定不變的, 會發生轉移;

(2)在V?p曲線或V?fr曲線中, 曲線形貌與經典Paschen曲線不同, 在曲線的左支和右支中間總會存在一個過渡區, 其擊穿電壓會表現出“上下波動, 近似持平”的特性;

(3)起始擊穿路徑的轉移方向總是表現為從較長路徑向較短路徑轉移.

5 討論

圖13 Case 5的計算輸入條件及計算結果(氣體工質： Ar)： (a) 電極結構及候選路徑劃分(f = 3.43); (b) V?p曲線的計算結果及起始路徑分布Fig. 13. The input conditions and calculation results in case 5 (working medium： Ar)： (a) The electrode geometry and potential path generation; (b) the calculation results of the V?p curve and the critical path distribution.

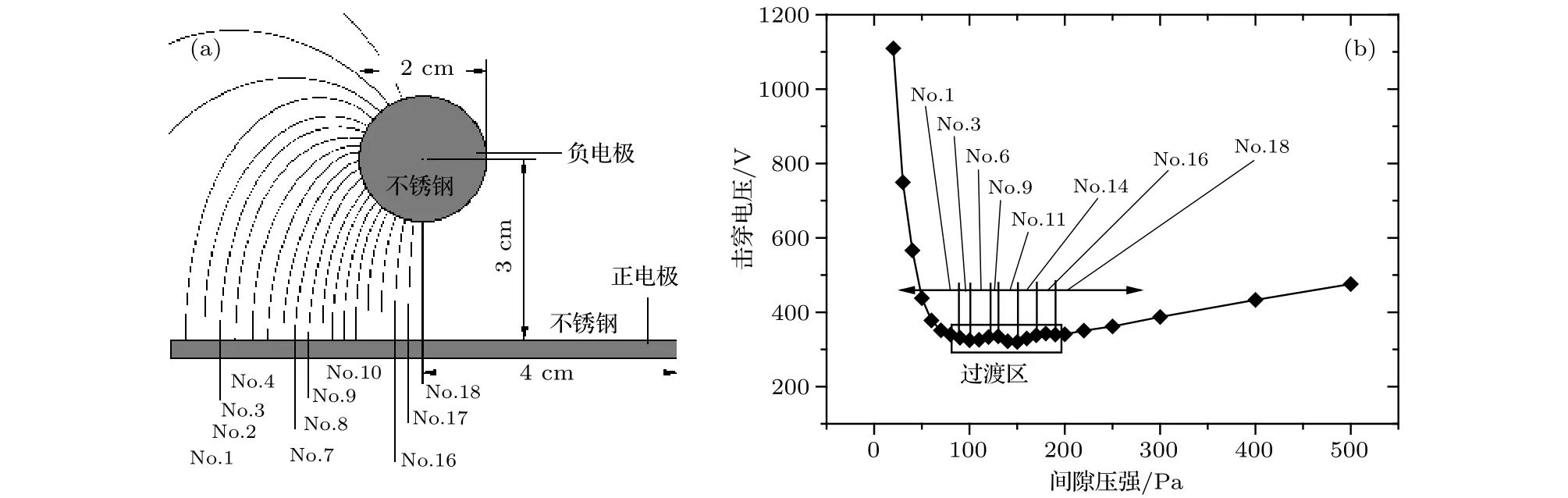
圖14 Case 6的計算輸入條件及計算結果(氣體工質： Xe) (a)電極結構及候選路徑劃分(f = 2.84); (b)V?p曲線的計算結果及起始路徑分布Fig. 14. The input conditions and calculation results in case 6(working medium： Xe)： (a) The electrode geometry and potential path generation; (b) the calculation results of the V?p curve and the critical path distribution.

結合試驗與仿真結果來看, 上述關于起始擊穿路徑的特性不應認為是一個巧合, 在以往學者的研究中[4,5,22?24], 也確實在擊穿試驗中觀察到了相似的試驗結果. 因此, 本節將深入討論上述兩個特性的內在機理.

5.1 路徑轉移原因和過渡區特性

以case 3為例, 利用DCP模型將case 3所有候選擊穿路徑的V?p曲線都計算出來, 并與整個電極的V?p曲線放在一起做對比(圖15).

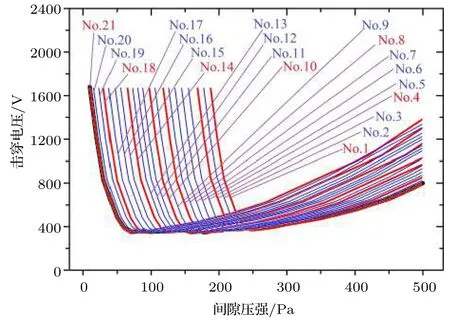
圖15 整個電極的V?p曲線形成原因(case 3)Fig. 15. The formation reason of the entire V?p curve in the whole gap of case 3.

圖15 所展示的藍色細線為沒有成為起始路徑的候選路徑的曲線, 而每一條紅色細線為各起始擊穿路徑的曲線, 黑色粗線為整個電極的曲線(圖11(b)的計算結果). 據圖15, 并不是所有候選路徑都有機會成為起始擊穿路徑, 只有那些可以達到全通道路徑中最低V?p曲線的路徑才能成為起始擊穿路徑, 并且, 每條起始路徑都僅僅在某個壓強范圍內具備成為當前起始擊穿路徑的條件, 而在其他壓強范圍內則不具備條件, 所以, 當壓強或氣體流率變化時, 起始擊穿路徑就會輪流更替, 發生“頻繁的路徑轉移”. 另一方面, 能夠成為起始擊穿路徑的候選路徑, 只能將自身V?p曲線的最優部分貢獻給整個電極的V?p曲線. 例如, No.21將其左支貢獻給黑色曲線, No.1將其右支貢獻給黑色曲線, 而No.14, No.10, No.8, No.4和No.1會在60–190 Pa之間輪流將自身的最小電壓區域(Paschen定律中稱之為(pd)min區域)貢獻給黑色曲線的過渡區. 因而, 過渡區每條起始路徑的(pd)min區域在電壓值上都是比較接近的, 取決于放電氣體種類和電極材料. 因此, 過渡區的擊穿電壓會表現出“上下波動,近似持平”的特性, 直到起始路徑轉移到最后一條路徑時, 曲線才會繼續上升.

5.2 路徑轉移方向

根據DCP數值模型, 判斷起始路徑的核心參數為每條候選路徑的總的二次電子發射數量nγ,而影響該參數的直接因素為每條候選路徑的總電離次數. 因此, 為揭示路徑轉移規律, 這里先給出不同壓強下, 各路徑中所引發的電離碰撞次數分布. 依然以case 3為例, 選擇No.18代表長路徑,No.4代表段路徑(參考圖11(a)), 選擇p = 40 Pa為低氣壓工況, p = 80 Pa為高氣壓工況. 利用DCP模型, 將每個計算節點的電離次數統計成云圖(圖16).

圖16 不同壓強下電極間隙的電離碰撞次數分布(case 3) (a) p = 40 Pa; (b) p = 80 PaFig. 16. The ionization collision number distribution at different gap pressures in case 3： (a) p = 40 Pa; (b) p = 80 Pa.

根據圖16, 發現在p = 40 Pa時, No.18的電離次數確實高于No.4, 在No.18附近有明顯的電子雪崩形態; 而在p = 80 Pa時, 情況正好相反.接著, 按照電離碰撞概率公式(第2節的8(b)式),有4個參數會影響電離概率Pion：,,和.與間隙壓強有直接關 系,和與 電 子 動 能有關, 而與路徑長度有直接關系. 那么, 對于case 3來說, 整個電極間隙都共享相同的, 如果和不變, 則長路徑的Pion將一直高于短路徑, 起始擊穿路徑將永遠是最長路徑, 而不應該轉移. 顯然, 這與試驗結果不符,由此來推斷, 應該是在不同的間隙壓強下和發生了變化. 因此, 下一步將繼續研究,和這3個參數在沿No.4和No.18路徑上的分布情況(圖17). 由于各計算節點的電子數量較多, 各電子的動能也不同, 所以圖17統計上述3個參數在各節點的平均值.

據圖17(a)–(d), 在低氣壓下, No.4和No.18的和分布并沒有顯著區別, 但是高氣壓下, No.4的和要明顯高于No.18. 形成該趨勢的直接原因可以由圖 17(e)和圖 17(f)解釋, 即 No.4和No.18的電子動能在低氣壓下相當, 但在高氣壓下No.18的電子動能明顯低于No.4. 接著, 這里繼續分析導致電子動能變化的原因： 能夠影響電子動能降低的因素除了電離碰撞以外, 就是激發碰撞. 因而, 圖18給出每個計算節點的激發碰撞次數分布.

圖18顯示： 在低氣壓工況中, 整個通道各候選路徑的激發碰撞次數幾乎相同, 并且碰撞次數較少, 這導致各個路徑的電子動能損失都較少, 于是就形成了圖17(e)的趨勢(No.4和No.18的電子動能相當); 但在高氣壓工況中, 激發碰撞次數在長路徑上明顯增多, 這是由于長路徑的較高, 其觸發的激發碰撞概率將明顯高于短路徑, 從而導致長路徑的電子動能損耗較大, 于是形成了圖17(f)的趨勢.

綜上, 激發碰撞所導致的能損影響是起始路徑轉移的關鍵因素： 在低氣壓下, 激發碰撞在各路徑的發生次數都較低, 其影響程度較小, 那么較長的路徑更容易觸發擊穿; 但隨著氣壓升高時, 激發碰撞在長路徑中的發生次數明顯升高, 其影響程度逐漸增加, 就導致起始路徑逐漸從長路徑向短路徑轉移.

圖17 在不同壓強、不同候選路徑上的分布規律, p = 40 Pa; (b)平均 , p = 80 Pa; (c)平均 , p = 40 Pa; (d)平均 , p = 80 Pa; (e)平均 , p = 40 Pa; (f)各節點的平均 , p = 80 PaFig. 17. The distribution of at different gap pressures and different potentialpaths in case 3： (a) The average , p = 80 Pa; (c) the average , p =40 Pa; (d) the average , p = 80 Pa; (e) the average , p = 40 Pa; (f) the average , p = 80 Pa.

圖18 不同壓強下電極間隙的激發碰撞次數分布(case 3) (a) p = 40 Pa; b) p = 80 PaFig. 18. The excitation collision number distribution at different gap pressures in case 3： (a) p = 40 Pa; (b) p = 80 Pa.

6 結 論

本文在先前學者的研究基礎上, 采用數值模型(DCP)與試驗相結合的方法, 對低氣壓起始擊穿路徑問題進行研究, 初步獲得稍不均勻電場(f =2.0–4.0)中, 起始擊穿路徑的存在位置規律以及相關機理：

1)在間隙壓強或氣體流率發生變化時, 起始擊穿路徑會發生轉移, 這與Osmokrovic的試驗結果吻合. 通過計算分析, 本文認為, 路徑轉移與每條候選路徑各自的擊穿電壓曲線特性有關, 整個電極通道總會在不同工況下選擇最可能發生擊穿的那條路徑來引發擊穿, 因此, 起始擊穿路徑會在不同壓強或流率工況下發生轉移;

2)在V?p或V?fr曲線中, 曲線左支和右支之間總會存在一個過渡區, 過渡區的擊穿電壓會表現出上下波動、近似持平的變化趨勢, 原因為過渡區的各起始擊穿路徑將其(pd)min部分貢獻給整個通道的擊穿曲線, 而這些(pd)min區域的擊穿電壓在數值上接近, 導致過渡區的曲線特性出現上下波動、近似持平, 只有轉移到最后一條起始擊穿路徑后, 曲線才會上升;

3)當間隙壓強或流率從低到高增加時, 起始路徑的轉移方向總會沿著較長路徑向較短路徑轉移, 這是因為較低氣壓下各候選路徑的激發碰撞次數均較少, 電子動能較高, 電離概率主要受路徑長度影響, 擊穿會選擇較長路徑, 而在較高氣壓下,較短路徑的激發碰撞次數明顯低于較長路徑, 其能損較低, 更易引發擊穿.