基于DSP的電動機保護補償式傅里葉算法研究
付強
1.安徽中電興發與鑫龍科技股份有限公司技術中心 安徽蕪湖 241008
2.安徽省電器設備電磁兼容(EMC)省級實驗室 安徽蕪湖 241008
3.安徽中電興發與鑫龍科技股份有限公司 安徽蕪湖 241008
半周積分算法,導數算法,兩采樣值積算法,三采樣值的積分算法,由于這些算法都是認為被采樣的電流和電壓是標準的正弦波,在設備正常運行工作時,一旦發生故障,常常是在基波出現的同時,伴隨著有衰減的非周期直流分量以及復雜的高頻分量,所以要求微機保護裝置預先濾去電壓、電流信號中的非周期分量和高頻分量,否則計算結果將遠遠偏離實際值,使計算誤差變大。雖然全波傅氏算法具有穩定性好的優點,在濾波過程中能夠濾除所有整數次的諧波分量,而且運算工作量比較小[1-2]。
1 補償式傅氏算法的計算推導步驟


通過以上新算法的整個計算推導過程,綜合分析可知,導致算法計算工作量較大的是半個周期后第3個采樣間隔中的數值,但是此種算法的計算時間僅僅約,完全可以滿足微機保護裝置實時控制的要求。補償式半波傅氏算法不但繼承了原由半波傅里葉算法的有點,而且又增加了對衰減非周期得直流分量的過濾功能。此種新算法所采用的數據窗僅僅為半個周期采樣值加上兩個采樣點,式算法的計算更加簡便,計算速度快,計算精度高,并且很好地濾除了衰減的非周期直流分量,而且此種功能又可以完全不受衰減的非周期的直流分量時間常數大小所限制[3]。
2 補償式全波及半波傅氏算法仿真
為了驗證以上算法的正確性、精度以及合適的應用范圍,對以上算法進行仿真并進行了比較:
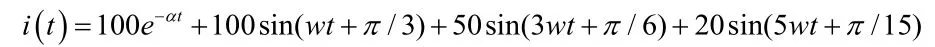
相應改變α,傅氏算法,補償式新傅氏算法算出的基波分量、角度的值及誤差如下表所示。

表1 各種算法的濾波效果比較
3 結語
綜上所述,補償式半波傅氏算法不但繼承了原有半波傅里葉算法的優點,而且又增加了對衰減非周期得直流分量的過濾功能。此種新算法所采用的數據窗僅僅為半個周期采樣值加上兩個采樣點,算法的計算更加簡便,計算速度快,計算精度高,并且很好地濾除了衰減的非周期直流分量,而且此種功能又可以完全不受衰減的非周期的直流分量時間常數大小所限制。

