運用CSEOF方法分析南海表面溫度季節與年際變化?

王冠楠， 鐘貽森， 周 朦， 劉海龍， 張召儒, 周 磊

(上海交通大學海洋研究院，上海 200240)

南海是西太平洋最大的邊緣海，水深超過5 500 m。它是一個半封閉的海盆，被中國，菲律賓，婆羅島，和中南半島包圍(見圖1)。海水通過臺灣海峽和呂宋海峽與中國東海和西太平洋交換，通過加里曼丹海峽與印度洋交換。由于流入南海的水主要來自穿過呂宋海峽的太平洋水，南海海水的水文性質變化與太平洋水存在密切聯系[1]。

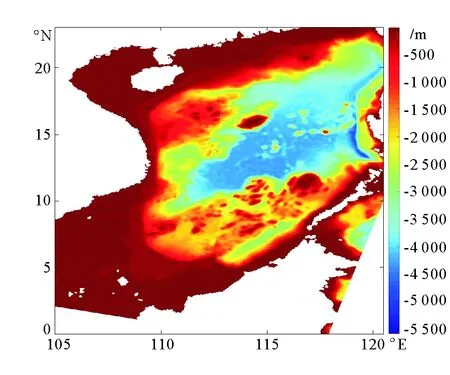
圖1 南海地形分布Fig.1 The topographic distribution of the South China Sea

關于CSEOF研究分析方法，目前已有一些研究應用在大氣海洋科學分析中。Wu等[20]基于CSEOF研究熱帶太平洋海域上層海洋熱含量的年際變化特征。Kim等[21]的研究指出，CSEOF方法可以分析北極海冰的損失與北極擴大機制的聯系。Sun等[22]用CSEOF和典型相關分析(CCA)發展了韓國降雨量預報的經驗統計系統。通過和觀測數據對比，證明CSEOF-CCA方法可以對韓國季節降水變化做有效預測。Kim等[23]以CSEOF方法為基礎分析朝鮮半島的驗潮數據和重構數據，并借此估計當地海平面變化。

1 數據和方法介紹

1.1 數據介紹

本研究主要結合衛星數據與高分辨率數值模擬結果進行分析，相對于衛星數據，模型的分辨率更高，可以較好的反映中尺度動力學特征，因此兩者對比也有助于本文了解中尺度過程的影響。本文使用的衛星數據來源于美國國家海洋和大氣管理局提供的最優插值海表溫度數據[24](Optimal Interpolation Sea Surface Temperature, OISST，https://www.ncdc.noaa.gov/oisst)。這組數據結合了多種觀測數據，包括衛星、船測、和浮標數據，通過插值建立成一個全球的網格數據，并使用偏值調節處理衛星和船測的數據，得到一個空間表面溫度圖。OISST的空間精度是0.25°，本文使用的空間范圍是100°E～120.5°E，0°～23°N。衛星數據的時間范圍是1982年至今，為了和模型數據能夠選取相同的時間區間，因此本文選取的時間范圍為1982—2007年。

模型數據來源于長期積分的高分辨率數值模型結果，本文使用區域海洋模型(Regional Ocean Modeling System, ROMS)對南海進行了5 km分辨率的模擬，該分辨率可以較好的模擬中尺度過程，因此對比衛星與模型數據結果也可以對中尺度過程的作用有所了解。模型垂直方向上分為50層，表層強迫來源于Coordinated Ocean-ice Reference Experiments Version 2 (CORE v2，http://data1.gfdl.noaa.gov/nomads/forms/core/COREv2.html)數據集，邊界條件與初始條件來源于Simple Ocean Data Assimilation (SODA 2.1.6，http://apdrc.soest.hawaii.edu/datadoc/soda_2.1.6.php)數據集。值得提及的是，模型未采用外部SST數據逼近的方式來矯正模型表面溫度場，模型海表面溫度變化主要受太陽輻射、氣溫及海洋過程影響。模型還包含了潮汐強迫，其數據來源于TPXO(http://volkov.oce.orst.edu/tides/global.html)全球潮汐模型[25]。本文加入模式分析意在觀察高分辨率的模型數據與粗分辨率的衛星數據的在CSEOF空間分布中的異同，研究中尺度過程對ENSO信號的響應。此外，由于衛星數據沒有潛熱通量、短波輻射熱通量以及海表面凈熱通量的數據，分析南海表面溫度延遲響應的物理機制時只能依賴模型數據。

1.2 循環平穩經驗正交函數分解法

將數據分解成不太復雜的模式使本文理解物理系統的復雜響應更加容易，最簡單且最常用的分解函數是經驗正交分解函數(EOF)。EOF定義如下：

EOF方法將數據T分解成由單一空間模態(LV)和相應時間序列(PC)組成的集合，LV是由一個隨機時間序列(PC)調制的物理過程。LV稱作負載向量，PC被稱為主成分時間序列(PCTS)。每一組負載向量和主成分時間序列組成一個簡單EOF模態。因此，EOF的每一模態的LV是時間獨立的，并且只有振幅隨著時間變化。然而，一個物理系統的特殊響應不是固定不變的，年周期信號出現在很多氣候變量中，它們以一年為周期振蕩，但是在年際尺度上同樣存在振幅的變化，引起了一個可調制的年際周期。

CSEOF不是簡單的特征值分解，普通EOF的協方差矩陣是不隨時間變化的，即假定信號是平穩的，這種假設在真實過程中往往并不成立，CSEOF將協方差矩陣設為一隨時間變化的給定先驗周期的函數。另外CSEOF特征值分解的本征函數不再是傅里葉函數，而是Bloch函數，是普通EOF的一種拓展[26]。Kim等[26]首次提出使用循環平穩EOF的方法分析地球物理信號中隨時間變化的空間模態和年際尺度的波動。CSEOF定義如下：

LV(r,t)=LV(r,t+d)。

CSEOF方法將空間時間數據T分解為由空間模態(LV)和相應的時間序列(PCTS)組成的模態。與傳統EOF相比，CSEOF最大的差異是空間模態LV是隨著時間改變的。模態間混合對于傳統EOF是普遍存在的問題，CSEOF可以更好的表現氣候信號并減少模態間的混合。近期的研究[27]已經證明了使用CSEOF可以有效的提取季節循環和ENSO信號，并且計算前不需要移除季節循環信號[26-29]。本文使用衛星與模型的月平均數據并以一年為固定周期時，每個CSEOF模態由12個負載向量和1個主成分時間序列組成。

2 結果與分析

2.1 模型數據驗證

為確保模型數據模擬的準確性，本文首先對比了衛星海表溫度數據(OISST)和ROMS模型數據的海表溫度，以及衛星AVISO數據和ROMS模型數據的海表面高度異常的季節平均和年際變化。

圖2和3分別是衛星數據和模型數據在1982—2007年期間的海表溫度季節平均。從圖中可以看到，總體上季節平均比較相似，在冬季，模型數據和衛星數據在南海西南部存在一個冷舌區域，這個現象與Liu等[30]文章中描述的南海西南部冷舌區域一致，主要是由于南海西邊界流帶來南海北部的冷水引起此處溫度較低，這個區域在11—2月比較明顯。在7—9月，模型數據中南海西南部越南沿岸存在一個較低溫度的區域，而衛星數據中并不明顯，這主要是由于在較高分辨率的模型中夏季西南季風引起的沿岸上升流帶來的冷水。

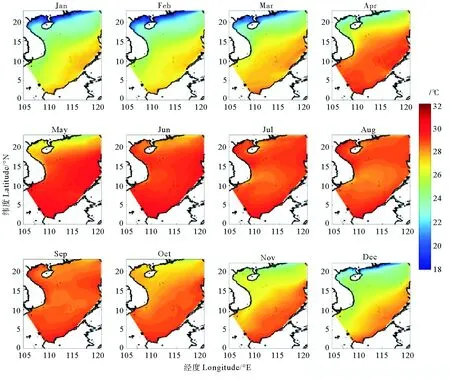
圖2 衛星數據表面溫度1982年到2007年季節平均Fig.2 The seasonal cycle of satellite data of sea surface temperature from 1982 to 2007

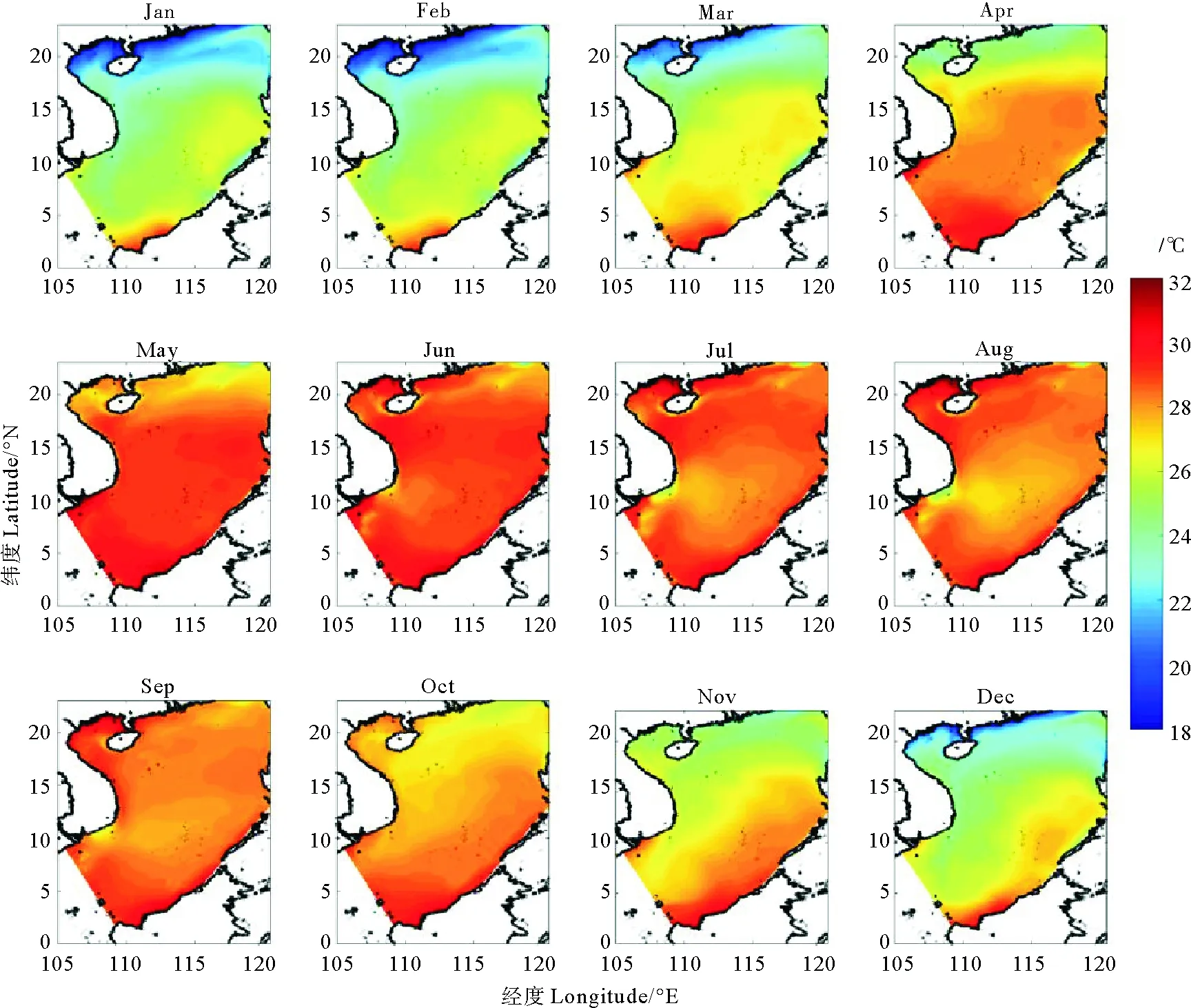
圖3 ROMS模型數據表面溫度1982年到2007年季節平均Fig.3 The seasonal cycle of ROMS model dataof sea surface temperature from 1982 to 2007

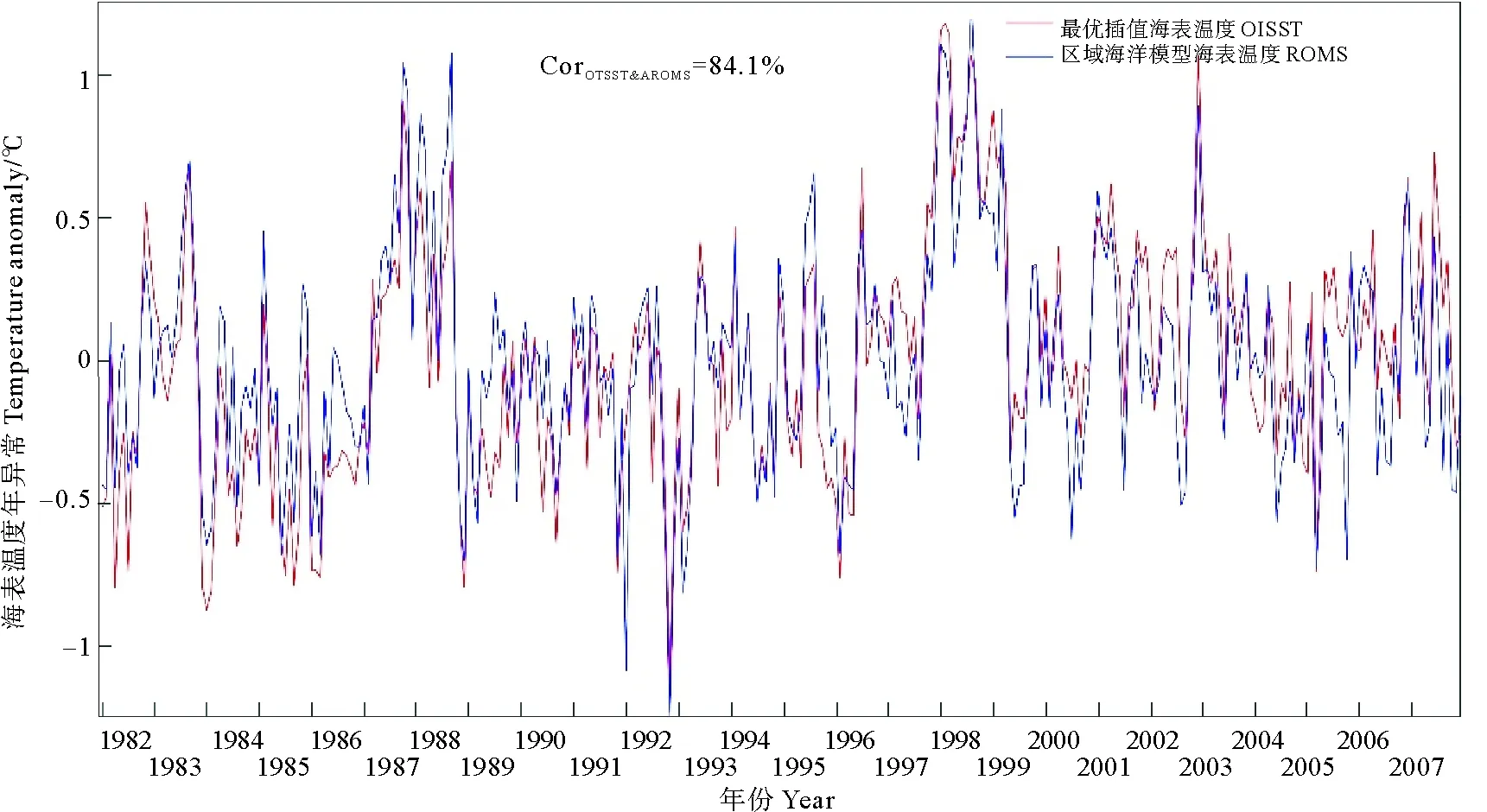
圖4 衛星數據和ROMS模型數據表面溫度年際異常Fig.4 Interannual surface temperature anomaly of satellite data and ROMS model data

圖5和6分別是衛星數據和模型數據的南海表面高度異常的季節循環。直接比較海表面高度，模型數據和衛星數據存在較大差異，其原因為模型數據和衛星數據選取的參考面不同。因此，使用海表面高度數據計算季節平均后，在每個點減去季節平均。對比圖5和6，模型數據對海表面高度異常的模擬較好。在冬季，海表面高度異常呈現西南部高，東北部低的特點；在夏季相反，海表面高度西南部低，東北部高。南海的動力學受到冬季的東北季風(11—2月)和夏季的西南季風(6—8月)影響[12]，這影響了海表面高度的季節循環。盡管兩種數據南海的表面高度異常季節平均相關性很好，但是由于模型不包含任何數據同化，表面高度異常的年際變化相關性較為一般。

2.2 南海表面溫度的年變化

Hamlington等[27]使用包含AVISO、Topex/Poseidon、OSTM等多種數據的衛星測高數據集證明了CSEOF分析可以從數據中提取出季節循環和ENSO信號。本文對衛星數據南海表面溫度數據做CSEOF分析，并將計算結果與ROMS模型數據的CSEOF結果對比。CSEOF的第一模態是季節循環信號，也是衛星數據和模型數據中的最主要模態。圖7是衛星數據南海表面溫度的CSEOF第一模態空間分布，去趨勢的衛星數據中，第一模態解釋了大約88.7%。Sun等[28]對北太平洋表面溫度使用CSEOF分解，第一模態解釋了95.68%，說明海表溫度的季節循環占所解釋的方差比重較大。第一模態空間分布的最大值和最小值分別在夏季(2月)和夏季(8月)的南海北部靠近廣東省附近，南海南部的振幅比較小。圖8是ROMS模型數據計算得到的CSEOF第一模態空間分布，這與圖7十分相似。模型數據第一模態解釋了約90%。在CSEOF第一模態的空間分布中，在冬季(12—3月)南海整體均為降溫變化，最大降溫出現在北部，存在達到-3 ℃的冷中心，南海南部降溫較小。在夏季(6—9月)南海整體均為升溫變化，最大升溫同樣在北部，存在達到3 ℃的暖中心。南海季節循環信號中，南海主要受太陽輻射影響，整體呈現同相變化的特征，振幅最大區域主要分布在北部灣和中國南部沿海地區，這主要受南海北部水深較淺的影響，使此區域更容易受到長、短波輻射以及水平平流的影響。在5、10和11月，南海的CSEOF第一模態南北部差異較小。6、7、8和9月在第一模態出現了北部高溫，南部低溫的特點，在季節循環中南北部差異不明顯(見圖2)。總體上，模型與衛星的季節平均空間分布非常相似，引入了中尺度過程未對季節信號產生顯著影響。

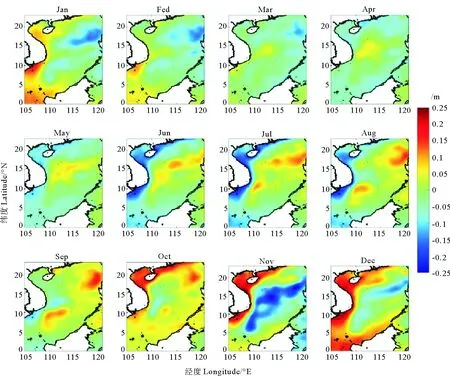
圖5 AVISO衛星數據1993—2007年表面高度異常Fig.5 The surface height anomaly of AVISO satellite data from 1993 to 2007

圖6 ROMS模型數據1993—2007年表面高度異常Fig.6 The surface height anomaly of ROMS model data from 1993 to 2007

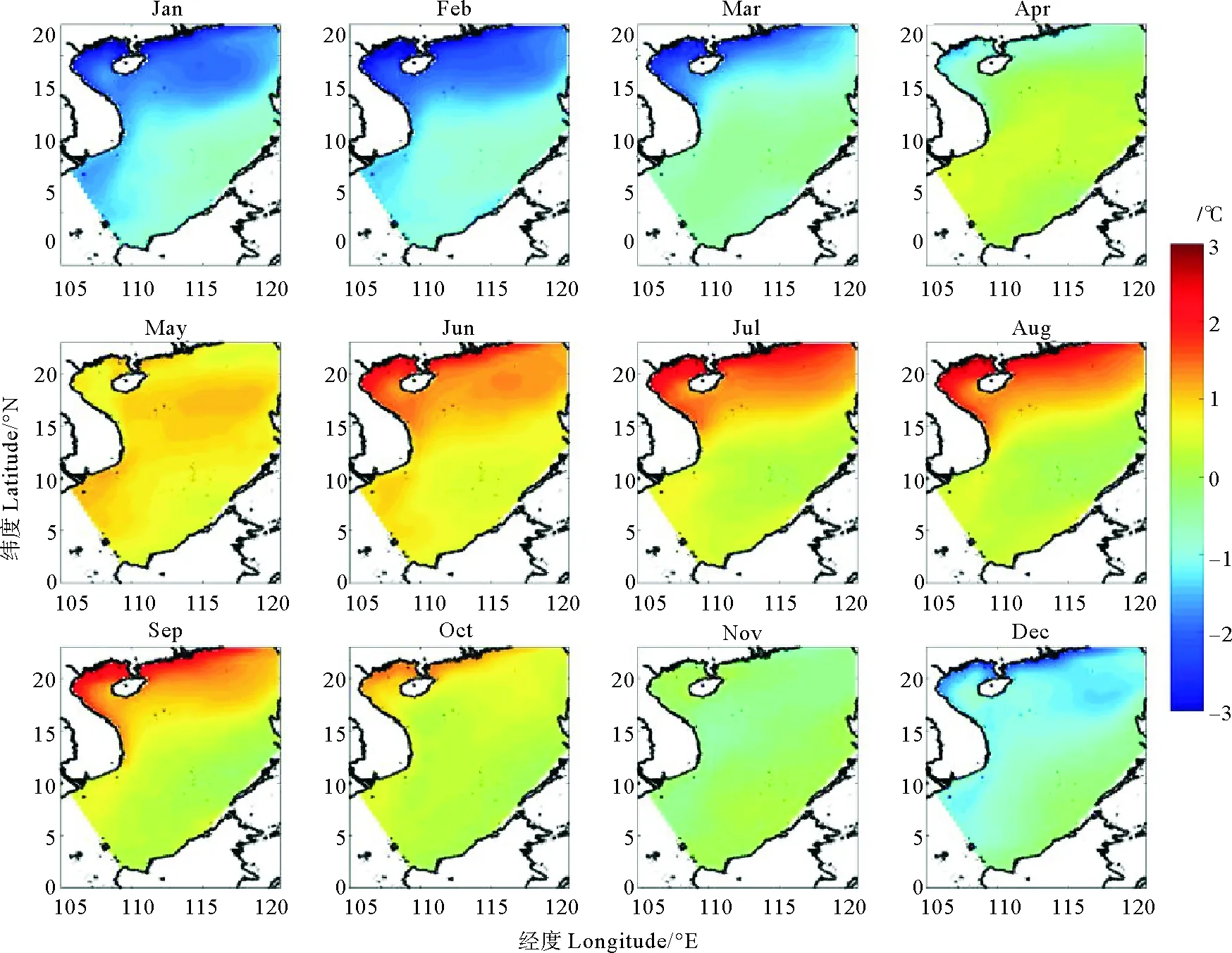
圖7 衛星數據南海表面溫度CSEOF第一模態空間分布Fig.7 The first mode space distribution of CSEOF based on satellite data of surface temperature in the South China Sea

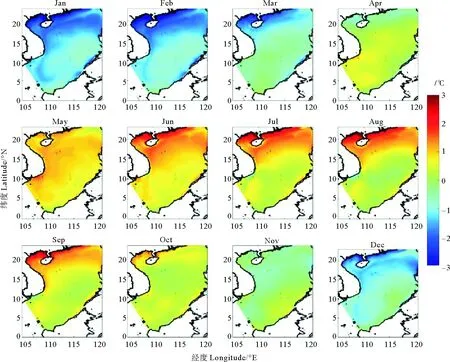
圖8 ROMS模型數據CSEOF第一模態空間分布Fig.8 The first mode space distribution of CSEOF based on ROMS model data of surface temperature in the South China Sea

2.3 ENSO信號

Cheng等[6]使用CSEOF方法分析南海表面高度的衛星數據、模型數據、潮汐表數據，發現CSEOF第二模態代表了ENSO信號的影響。圖10為衛星數據計算得到的CSEOF第二模態，解釋了約3.6%的方差。圖11是模型數據第二模態空間分布，解釋了約2.14%方差。

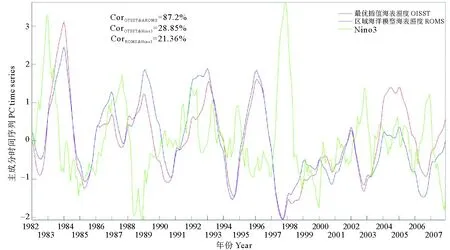
圖9 衛星數據和模型數據CSEOF第一模態時間序列與Nino3指數對比Fig.9 The comparison of the Nino3 index and the first mode time series of CSEOF based on the satellite data and the model data

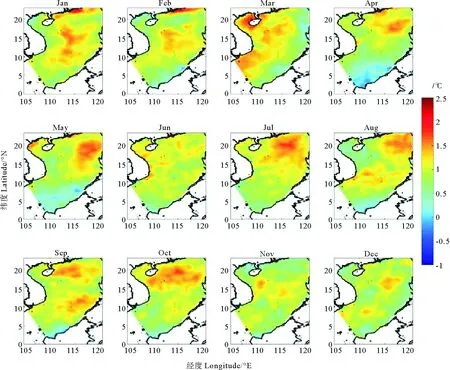
圖10 衛星數據南海表面溫度CSEOF第二模態空間分布Fig.10 The second mode space distribution of CSEOF based on satellite data of surface temperature in the South China Sea

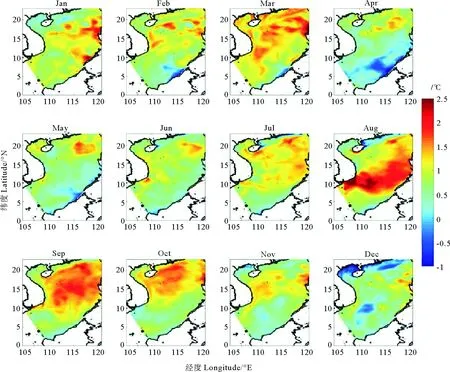
圖11 ROMS模型數據南海表面溫度CSEOF第二模態空間分布Fig.11 The second mode space distribution of CSEOF based on ROMS model data of surface temperature in the South China Sea

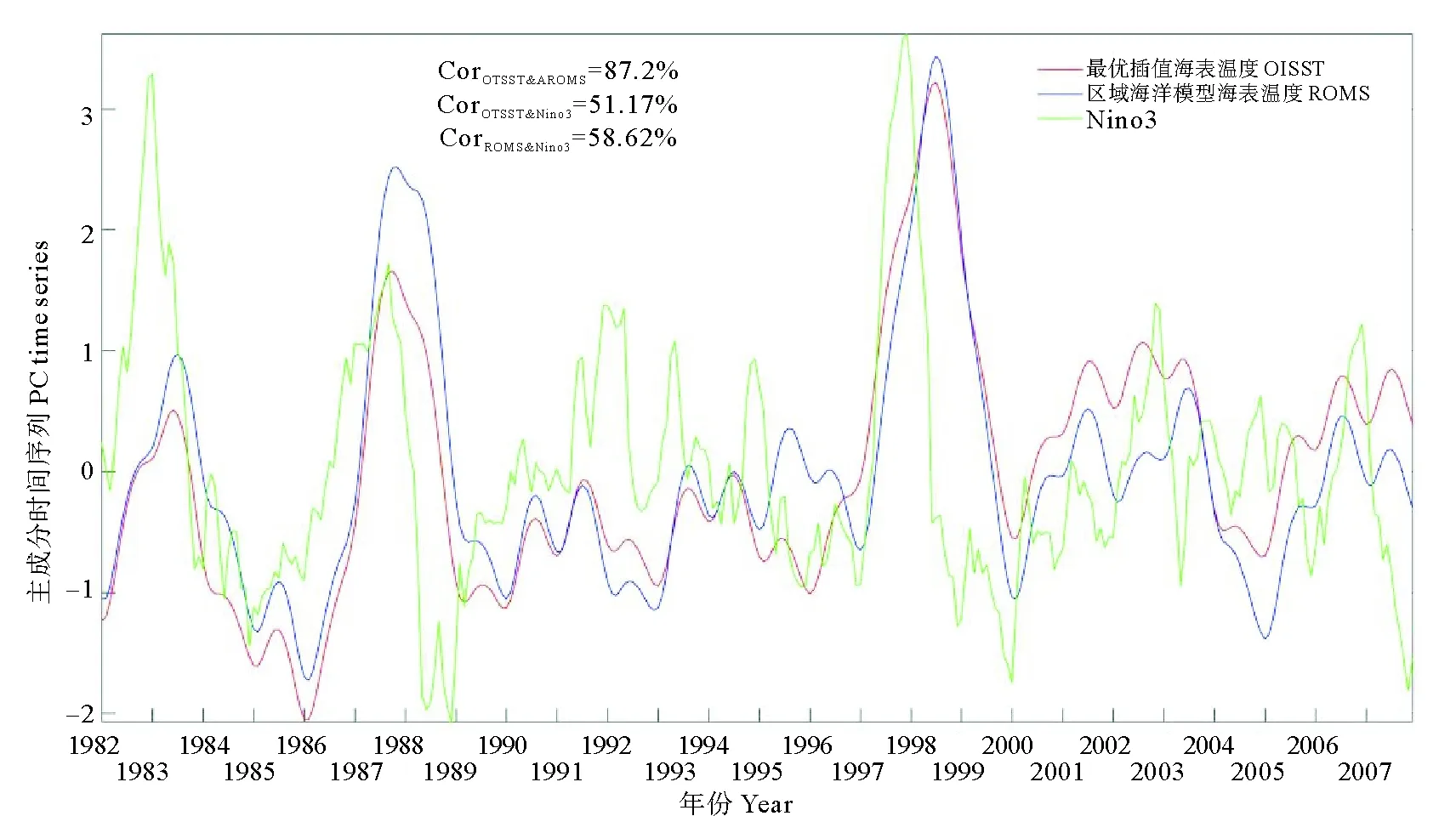
圖12 衛星數據和ROMS模型數據的CSEOF第二模態以及與Nino3指數對比Fig.12 The comparison of the Nino3 index and the second mode time series of CSEOF based on the satellite data and the model data

2.4 ENSO遠程影響物理機制的探究

海洋表面蒸發的熱量直接對應潛熱通量，海洋上空云覆蓋的改變直接影響太陽短波輻射的熱量。因此為了驗證“大氣橋”理論，本文對ROMS模型數據中的潛熱通量和太陽短波輻射熱通量做CSEOF分析。潛熱通量CSEOF前二模態占比分別為65.86%和6.62%；太陽短波輻射熱通量的CSEOF前二模態占比分別為81.29%和4.43%。通過潛熱通量和短波輻射熱通量前二模態的主成分時間序列與Nino3指數的滯后相關性分析發現，潛熱通量的第一模態和短波輻射熱通量的第二模態與Nino3指數相關性高。蒸發引起的潛熱通量的季節循環不夠明顯，可能引起ENSO對潛熱通量的季節信號影響較大，因此潛熱通量的第一模態主成分時間序列與Nino3指數相關性高。

圖13是潛熱通量CSEOF第一模態主成分時間序列，太陽短波輻射CSEOF第二模態主成分時間序列以及Nino3指數的對比。通過滯后相關性分析，可以確定Nino3指數與潛熱通量和太陽短波輻射熱通量的時間序列在無滯后時間時相關系數最大。其中，Nino3指數與潛熱通量的相關系數為38.41%，與太陽短波輻射的相關系數為62.05%。KLEIN等[2]提出了一個假設，海表面溫度異常對云層覆蓋和蒸發的響應符合下面的公式：

式中：SST′是表面溫度異常值；F′是凈表面通量的異常值，即由云層覆蓋和蒸發異常引起的表面通量變化；ρ是海水密度；c是海水的比熱；H是混合層深度；λ是滯后的時間尺度。上述公式表達了混合層中的垂直對流過程，溫躍層下的夾帶過程過程或者是任何與ENSO無關的過程可能是阻礙海洋表面溫度過快反映于凈熱通量的原因。為了確認混合層對于表面溫度變化的延緩作用，對ROMS模型數據表面凈熱通量與混合層深度的比值做CSEOF分解。Qiu等[31]分析了5種計算混合層深度的方法，并對比南海北部不同方法得到的混合層深度，得到溫度方法是計算該區域更好的方法的結論。鑒于其研究區域與本文相似，采用了相同的方法計算混合層深度，即與表層溫度差為0.6 ℃的深度。圖14是凈熱通量與混合層深度比值的CSEOF第二模態時間序列與Nino3指數的對比，通過滯后相關性分析發現，在Nino3指數領先9個月時，相關系數最大，達到49.96%。模型數據表面溫度滯后Nino3指數為8個月，盡管結論與表面溫度不盡相同，不可否認的是混合層與凈熱通量共同延緩了表面溫度的過快響應。

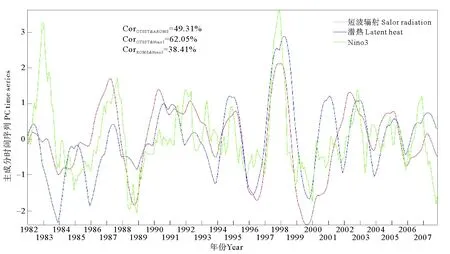
圖13 南海表面潛熱通量的CSEOF第一模態時間序列以及表面太陽短波輻射CSEOF第二模態的時間序列與Nino3指數對比Fig.13 The comparison of the Nino3 index and the first mode time series of surface latent heat flux and the second mode time series of surface short wave radiation in Southern South China Sea

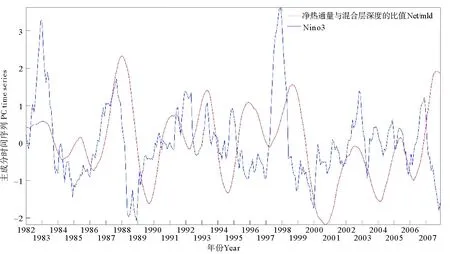
圖14 南海表面凈熱通量與混合層深度比值的CSEOF第二模態的時間序列與Nino3指數對比Fig.14 The comparison of the Nino3 index and the second mode time series of the ratio of net surface heat flux to mixed layer depth in the South China Sea

3 總結與討論

本文選取Nino3指數比較南海表面溫度與ENSO的關系，此外，表面溫度和Nino3.4指數以及Nino4指數的關系同樣存在一定的滯后相關性。其中，Nino3.4指數領先表面溫度第二模態時間序列8個月時，相關性最高，模型數據相關系數為51%，衛星數據為43.36%。Nino4指數領先表面溫度第二模態時間序列9個月時相關性最高，模型數據相關系數為36.8%，衛星數據為33.13%。