靜水中并列振蕩雙圓柱水動力學性能及機理?

及春寧, 譚沛森， 仵柏衡

(1.天津大學水利工程仿真與安全國家重點實驗室，天津 300072； 2.中國海洋大學海洋與大氣學院，山東 青島 266100； 3.挪威科技大學海洋技術系，挪威 特隆赫姆 7491)

振蕩流中的靜止圓柱以及靜止流中的振蕩圓柱在海洋工程和水動力學領域有著極大研究價值。該物理模型適用于很多海洋工程設施，如研究液化天然氣運輸船在受到波浪力擺動時，液艙中泵塔的受力；由多個圓柱組成的波能吸收器在波浪中的振動；水下防噴器受到擾動在流速較小的海水中的振蕩[1]等。對于上述工程應用，渦激振動產生的力學問題會對建筑設施產生極大的影響，忽視這種影響可能釀成災害性后果，因此研究圓柱體在振蕩過程中的受力載荷至關重要。實際工程中，圓柱的數量和擺放方式各異，而并列排布的雙圓柱系統是其中較為典型的一種。對雙圓柱體在振蕩過程中的受力載荷研究對于大量的實際工程應用問題具有突出的指導意義。

該問題的流體動力學模型可以簡化為振蕩流體中的結構物相互作用。該結構上沿振動方向的力可以由莫里森方程表示:

而垂直于振動方向的力可以表示為：

其中：Cd為阻力系數；Cm為附加質量系數；Cl為升力系數。Keulegan[11]指出，這三個關鍵的水動力學系數依賴于無量綱數KC。KC數被定義為KC=UmT/D，Um為圓柱最大的振蕩速度，T是圓柱的振蕩周期，D為圓柱直徑。在簡單正弦振動中，KC數可以簡化為2πA/D,A為圓柱振蕩的振幅。Sarpkaya[12]指出，這三個水動力學系數不僅依賴于KC數，也同時依賴于另一個無量綱數β，β被定義為β=D2/Tν，ν為流體的運動學粘度系數。因為雷諾數Re定義為Re=UmD/v因此雷諾數Re也可表示為Re=β×KC。

單個圓柱在均勻流中的水動力特性已經得到了廣泛的研究。Bearman等[3]實驗測量了KC數范圍為4～55和β范圍為100～166時的圓柱體上的流體力合力，小KC數范圍內，阻力系數Cd與理論結果吻合較好。Sarpkaya[4]實驗在穩定流場所對應的KC數范圍下，合理的預測阻力系數和附加質量系數隨著KC數上升的變化趨勢。Tatsuno和Bearman[5]在不同的KC數值下進行了實驗，并確定了8種不同的流動狀態。

與單個圓柱相比，多體圓柱在靜止流場中振蕩的水動力特性會復雜很多。這是圓柱的尾流之間的相互作用所導致的。對于串聯圓柱系統，下游圓柱受到上游圓柱尾流作用，在間隙比較小時會產生馳振現象(Wake-induced galloping)[6]。Chen等[7]對雷諾數為100，間隙比為2.0～5.0的雙圓柱系統進行了數值模擬，并分析了不對稱振動的現象。為了進一步研究雙圓柱系統水動力特征和其受力載荷，本文首先進行了了靜水中振蕩的并列雙圓柱動力特性的模型實驗。此外，為了更好的理解雙圓柱的流場特征及其機理，本文同時對并列雙圓柱系統在靜止流場中的運動進行了數值模擬，從能量的角度對阻力系數增大進行了機理分析。

1 實驗設置

1.1 實驗裝置與器材

本研究實驗在麻省理工學院拖曳水池實驗室的拖曳水池中進行，研究靜水中振蕩圓柱的水動力特性，實驗整體布置如圖1(a)所示,水池長1.5 m，寬和高均為1 m。實驗所使用圓柱的表面經過電鍍，以保持其表面光滑，從而減小因表面粗糙引起的誤差，圓柱直徑包括2.54、3.81、5.08與6.35 cm。圓柱被固定在拖曳平臺上，拖曳平臺與力傳感器相連；拖曳平臺下方有2個滑輪，實驗時，由電腦控制的拖曳平臺在搭建在水池上方的平板上做正弦式往復運動。只有圓柱浸入水中，其他的裝置均不會對圓柱的水動力學結果產生影響。實驗使用ATI Gamma六分力傳感器對力進行實時記錄。本次實驗采用直徑為3.81 cm的圓柱，與該尺寸的圓柱相比，實驗水池范圍(1.5 m×1 m×1 m)足夠大，當圓柱在水池中心位置處振蕩時，產生的渦街和尾流無法傳播到水池邊界處，因而可忽略邊界效應，將該振蕩視為圓柱在無限大的水域中進行的振蕩。并列圓柱的布置如圖1(c)所示，L為兩圓柱之間的間隙，D為圓柱直徑，為了便于說明，實驗引入間隙比(gapratio=L/D)的概念，即兩圓柱間距與圓柱直徑的比值。振動位移隨時間的變化可表示為x=Asinωt,其中，A是振幅，ω是振動的角速度。

1.2 實驗數據選取

振蕩圓柱體在靜止流體中所受的力可以被分解為2個部分，第一部分為沿振動方向的力，可以用莫里森方程表示：

第二部分為垂直于振動方向的力(稱為升力)，可以表示為：

圖1 實驗布置和模型Fig.1 Experiment setup and models

其中Cd、Cm和Cl分別是阻力系數，附加質量系數和升力系數。三者主要由KC數(2πA/D)、β數(D2/Tυ)和間隙比(L/D)三個無量綱數決定，其中，T是振動周期，υ是流體的運動學粘度系數。實驗中，KC數從1～20變化，β數的選取范圍是350～2 810。雙圓柱的間隙比設定為0.5、1.0、2.0和3.0。每個實驗工況重復3次，以保證實驗結果的可靠性。

2 實驗結果與分析

2.1 實驗驗證

并列排列，KC=12.1，β=550，L/D=0.5。

圖2給出了在靜水中，并列雙圓柱(直徑5.08 cm，間隙比0.5，KC數12.1，β數550)的位移和阻力系數Cd隨時間的變化圖中，圓柱的位移隨時間正弦變化，阻力呈現多頻變化，且相位落后于位移。

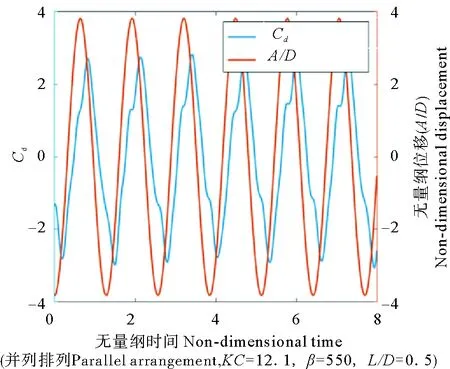
圖2 無量綱位移和振動方向的 阻力系數隨著時間的關系Fig.2 non-dimensional motion and drag force vs non-dimensional time

Bearman和Sarpkaya分別對振蕩流體中的靜止圓柱進行了類似實驗，圖3比較了本文結果與Sarpkaya[7]的結果，可以發現兩組實驗的趨勢相同，但數值上一定差異。兩組實驗的區別在于，在Sarpkaya[7]的實驗中，靜止圓柱被置于振蕩流場中，而本次實驗是將做標準正弦振蕩的圓柱置于靜止流場。此外，兩組實驗選取的β數略有差異(本文實驗β數為1 400，Sarpkaya[7]中β數為1 380)。然而兩種實驗方法的結果都表明，隨著KC數的增加，附加質量系數Cm有所下降，而阻力系數Cd基本呈上升趨勢。

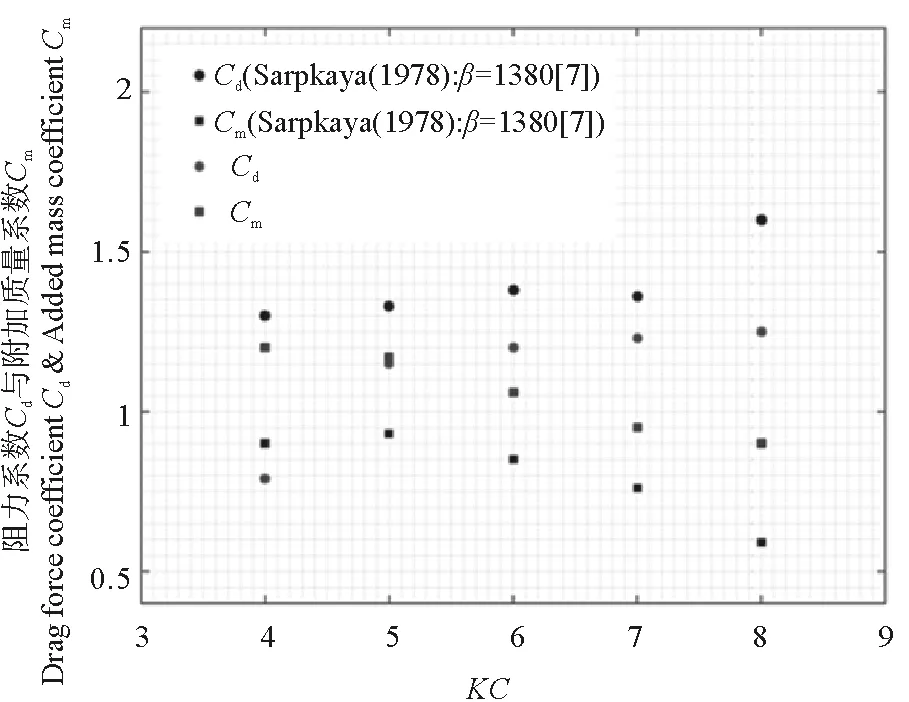
(本次研究β=1 400; Sarpkaya: β=1 380[7])圖3 Cd和Cm隨著KC數的變化以及 本次實驗和Sarpkaya實驗結果對比Fig.3 Comparison of Cdand Cm vs KC number between our experiment β=1 400 and Sarpkaya’s experiment β=1 380

2.2 阻力系數

阻力系數Cd是莫里森公式中的一個關鍵系數。與單圓柱相比，雙圓柱系統在流場中振蕩時，兩圓柱之間會產生相互作用，因而會使得并列雙圓柱的流場比單圓柱的復雜。圖4(a)和(b)分別給出了β數為550和720工況，不同間隙比情況下的平均阻力系數Cd隨著KC數的變化。隨著間隙比減小，雙圓柱平均阻力系數Cd有增大趨勢，在間隙比為0.5(試驗中所采用的最小的間隙比)，KC數大于5時，阻力系數Cd明顯大于單圓柱振蕩時的阻力系數Cd。而在KC數較小(3,4)時，二者差異不大。這是由于正弦振蕩中的圓柱，KC數可以表示為KC=2πA/D，A是圓柱振蕩的振幅，D是圓柱的直徑，小KC數對應的圓柱振幅較小，激發的尾流較弱，雙圓柱之間的相互作用因而也相對較弱，很難觀察到阻力系數Cd的增強現象。當間隙比較大(3.0)時，兩者數值相近。這是由于當兩個圓柱距離較遠時，兩圓柱之間的水動力相互作用很弱，故呈現出與單圓柱相一致的水動力特性。

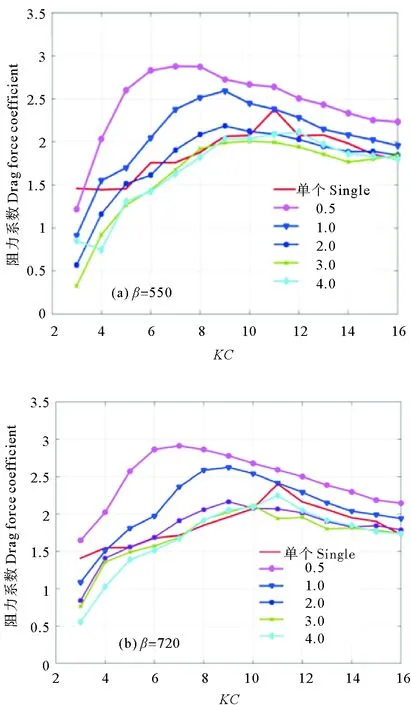
圖4 不同間隙比下的并列雙圓柱平均阻力系數 Cd隨KC數的變化Fig.4 Drag coefficient vs KC number under different gap ratio

2.3 附加質量系數

附加質量系數Cm是莫里森公式中的另一個關鍵系數。由于雙圓柱振蕩引起的流場與單個圓柱的流場不一致，流體質點的運動情況發生了明顯變化，從而導致附加質量系數Cm不同。

圖5 不同間隙比下的并列雙圓柱平均 附加質量系數隨KC數的變化Fig.5 Added mass coefficient vs KC number under different gap ratio

圖5(a)和(b)分別給出了β數等于550和720時，附加質量系數Cm隨KC數的變化。由圖可見，Cm隨著KC數的增大而基本呈減小趨勢；且圓柱之間的距離越近，附加質量系數Cm越大。與阻力系數Cd類似，當間隙比較大(3.0)時，由于兩個圓柱相互作用弱，因此附加質量系數Cm也與單個圓柱的情況相類似。但是在間隙比為0.5時，盡管在小KC數下兩者數值相近，但是當KC數大于6時，0.5間隙比下雙圓柱的附加質量系數明顯大于單圓柱的附加質量系數，而且前者很快趨于平穩。

同時，圖5(a)和(b)顯示，同樣的β數下，當間隙比為1.0時，Cm約在KC數等于6時開始趨于穩定。當間隙比為2.0時，Cm約在KC數等于8時趨于穩定。當間隙比為3.0時，Cm約在KC數等于11時趨于穩定。單圓柱的情況下(也可以理解為間隙比為∞)，β=550時，Cm在實驗的KC數范圍內未出現穩定，β=720時，Cm在KC數等于13時趨于穩定。很明顯，隨著間隙比的增大，Cm在更大的KC數達到穩定。在到達穩定之前，Cm隨著KC的增加而減小。

2.4 升力系數

圖6為β數為550時，不同間隙比下的升力系數的均方根Cl, rms隨KC數變化的情況。

由圖可知，在KC數等于5～10的范圍內，并列圓柱的升力系數均方根值要大于單圓柱的。同時，隨著KC數的增大，升力系數均方根值逐漸降低，但存在波動，而且間隙比越小,該波動對應的KC數也越小。比如單個圓柱的波動出現在KC數等于11的位置，間隙比為1.0的情況中，波動出現在KC數等于7的位置，而間隙比為0.5的情況中，波動出現在KC數等于6的位置。

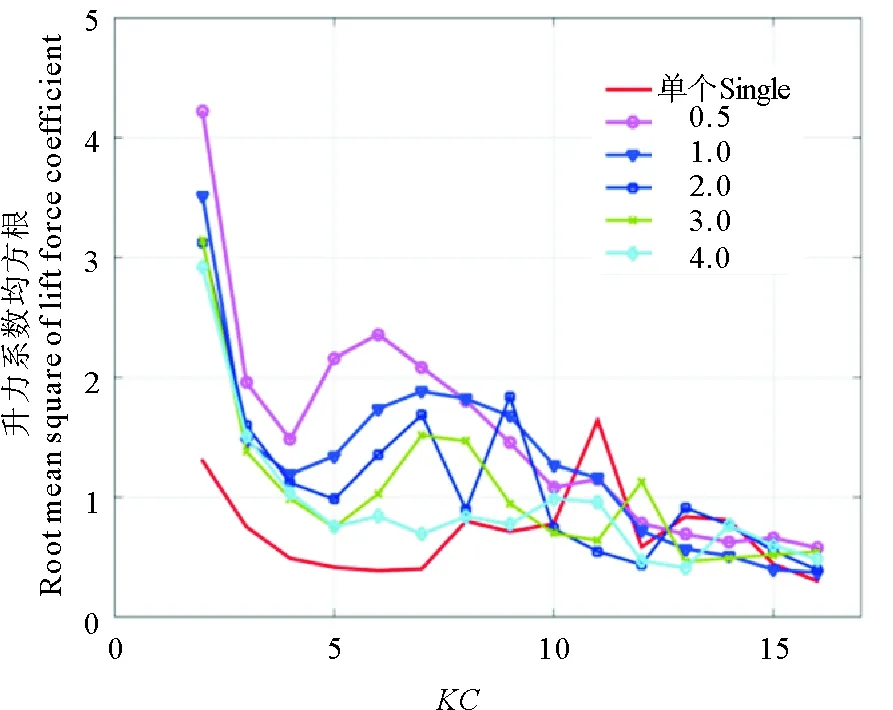
圖6 β=550時，間隙比為0.5～4.0 下升力系數均方根隨KC數的變化Fig.6 Root mean square of lift force coefficient vs KC number (β=550, gap ratio=0.5～4.0)

為進一步對比并列圓柱和單圓柱阻力系數Cd和升力系數Cl的不同，實驗選取單圓柱(KC=9，β=550)，將所測升力系數Cl和阻力系數Cd的時域數據經過傅立葉變換，得到Cl和Cd的頻譜(見圖7)。可以看到，兩個系數的一階頻均在0.77處，同時升力系數Cl在1.55(約二倍頻率處)處出現了明顯的二階分量，且二階分量占優。阻力系數Cd在2.33處出現較明顯的二階分量(約三倍頻率處)，但一階分量占優。

此外，對β=550條件下，不同KC數(1～20)的單圓柱和雙圓柱(L/D=0.5)的實驗數據進行傅立葉變換，得到x坐標為階頻數，y坐標為KC數，z坐標為譜密度的3D頻譜圖(見圖8、9)。

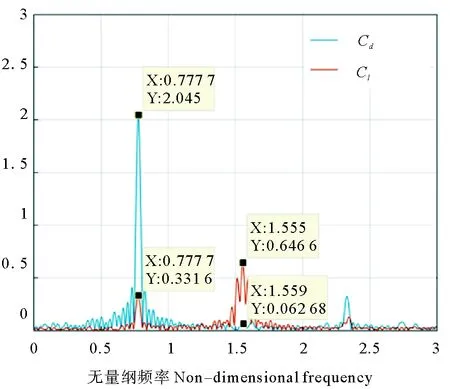
圖7 單圓柱(KC=9,β=550) 情況下Cl和Cd的傅里葉頻譜Fig.7 Fourier spectrum for single cylinder (KC=9, β=550)

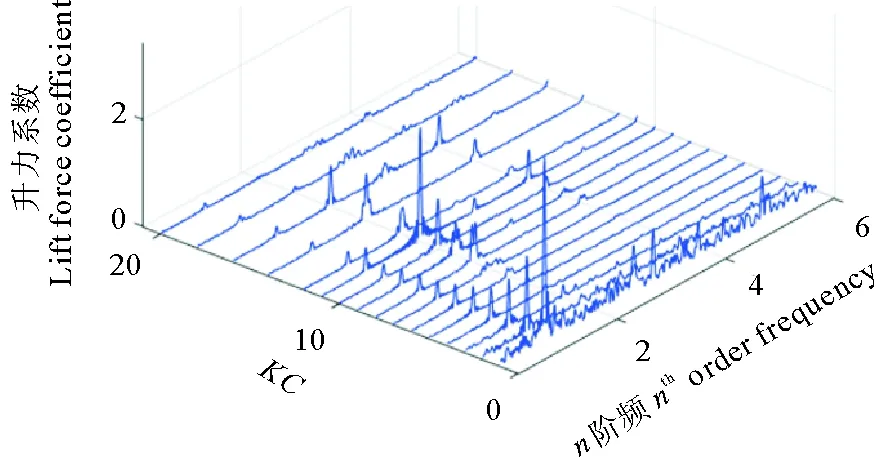
圖8 單個圓柱情況下傅里葉變化 得到的Cl頻譜圖

圖9 雙圓柱并列振蕩情況下(間隙比0.5)傅里葉 變化得到的Cl頻譜圖Fig.9 Fourier spectrum for dual cylinders’ lift coefficient (gap ratio=0.5)

對比圖8、9，可以看到單圓柱情況下，隨著KC數的增大，圓柱的升力系數頻率先是一階占優，而后逐漸過渡到二階占優(KC=11)。并列圓柱情況下，升力系數主要表現為二階頻率占優，并且存在較為明顯的四階頻率分量。

3 數值模擬結果與分析

由于在水槽中進行的實驗很難將流場清晰地展現出來，因此，為了進一步分析雙圓柱并列振蕩和單圓柱振蕩的流場特征，本次研究開展了基于BDIM(Boundary Data Immersion Method)的數值模擬，得到不同振蕩形式下的流場實時數據和流場的渦量云圖。研究將通過數值模擬實時數據計算升力系數、阻力系數和附加質量系數，并設置控制體，從能量的角度解釋水槽實驗中阻力系數增大的現象。Zhao[10]的研究證明，與三維模型相比，二維數值模型也能夠清晰的描繪出流場特征并準確的計算圓柱的水動力學載荷，因此，本次研究使用二維模型進行模擬。

數值模擬的計算中將所有物理量都無量綱化：(x,y)=(x’,y’)/D、 (u,v)=(u’,v’)/Um、p=p’/ρUm、t=Umt’/D。 (x,y)是網格上的坐標。 (u,v)是x、y方向上的速度分量t、p、ρ和Um分別是時間，壓強，流體密度和圓柱的最大振蕩速度，則無量綱化的控制方程化為：

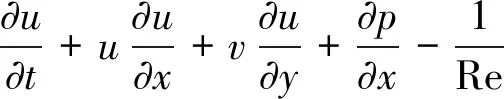
數值模擬布置如圖10所示，虛線表示控制體的邊界。控制體長度為8D，寬度為4D，以滿足大運動幅度的要求。因為數值模擬的邊界是不可穿透的，因此將計算域的大小設置為40D×20D，以達到消除邊界效應和阻擋效應。 Lily-Pad的求解器不需要我們建立網格，屏幕的像素將直接成為網格的節點并建立非結構化網格。然而，求解器要求必須以像素為單位定義柱面和計算域的大小，因此在計算中，為了平衡計算效率和精度，每個圓柱體的直徑D被設置為50個像素。

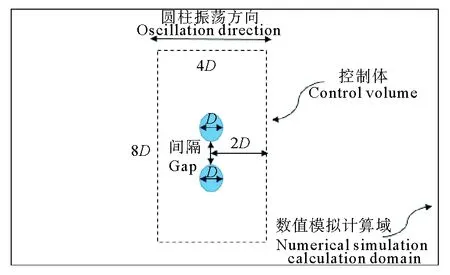
圖10 數值模擬布置圖Fig.10 Numerical simulation setup

4.1 正確性和收斂性驗證

首先采用三種不同全局精度的網格(delta/D=0.025、0.02和0.016)對振蕩單圓柱繞流進行數值模擬，以檢驗網格的收斂性。收斂性驗證中，KC數目設置為6，雷諾數Re設置為120。計算所得的附加質量系數和阻力系數見表1。以delta/D=0.016所得到的Cm值(1.975)和Cd值(1.979)為參考，計算不同網格精度條件下，附加質量系數Cm和阻力系數Cd的相對誤差和。

由表1可知，與delta/D=0.016的工況相比，delta/D=0.02工況的附加質量系數的相對誤差為0.2%，阻力系數的相對誤差為0.56%。相比之下，delta/D=0.025工況的附加質量系數的相對誤差為6.26%，阻力系數的相對誤差為8.38%，遠大于delta/D=0.02工況的相對誤差，證實了delta/D=0.02的網格滿足收斂性要求。圖11(b)和(c)進一步給出了delta/D為0.02和0.016時，圓柱向右以最大速度通過平衡位置的的渦量云圖(其相位定義為π/2)，可以看到兩者幾乎相同。然而，圖11(a)中delta/D為0.025的結果明顯不同，流線對稱，未觀察到圓柱兩側交替泄渦現象。

為了證明數值模擬算法的正確性，在進行數值模擬研究前，研究首先使用前人在精度更高的網格上計算得到的結果進行比對：另取與Tong[9]相同的工況參數設置，即KC數為5、雷諾數Re為100，并將該工況下使用三種精度更高的網格計算得到的Cm和Cd的結果和Tong[9]進行對比，見表2。

表1 網格收斂性驗證Table 1 Grid convergence verification

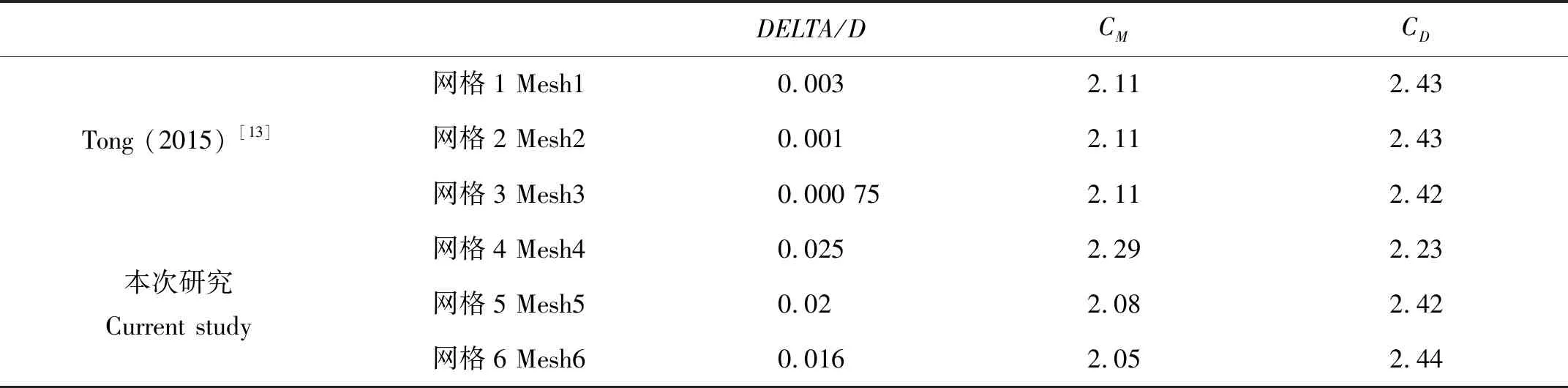
表2 Tong(2015)[9]數值模擬參數和本次數模擬參數的對比Table 2 Comparison between Tong (2015)[9] numerical simulation parameters and current simulation parameters

Tong[9]設置的三種網格delta/D分別為0.003, 0.001, 0.000 75，其精度較本次研究使用的網格更高，其計算得到的(Cd，Cm)分別為(2.11，2.43)、(2.11，2.43)、(2.11，2.42)、最終Tong[9]選取了網格2即delta/D為0.001的網格進行數值模擬。與網格2相比對，本次研究中網格4計算的結果(2.29，2.23)與之差距較大，網格5得到的Cd和Cm略小于網格2計算的結果，網格6計算的Cd小于網格2計算的Cd，而Cm略大于網格2。同時，與網格6相比，網格5計算的Cd更接近于Tong[9]使用的精度更高的網格2的Cd值。因此網格5和網格6滿足收斂性驗證，且其計算結果與前人在精度更高的網格上的計算結果更為接近，滿足正確性驗證。同時，從網格5和網格6中都可以觀察到交替泄渦的現象。為了提高運算效率，研究采取網格5(delta/D=0.02)進行數值模擬計算。

3.2 阻力系數Cd分析

在并列雙圓柱的數值模擬中，雷諾數Re選定為120，KC數為6，β數(Re/KC)為20，間隙比選定為0.50、0.75、1.00、1.25、1.50、2.00和3.00，同時選取單個圓柱振蕩進行對比(見圖12)，圖中的虛線所對應的縱坐標值代表同一KC數和β數下的單個圓柱阻力系數Cd的值。

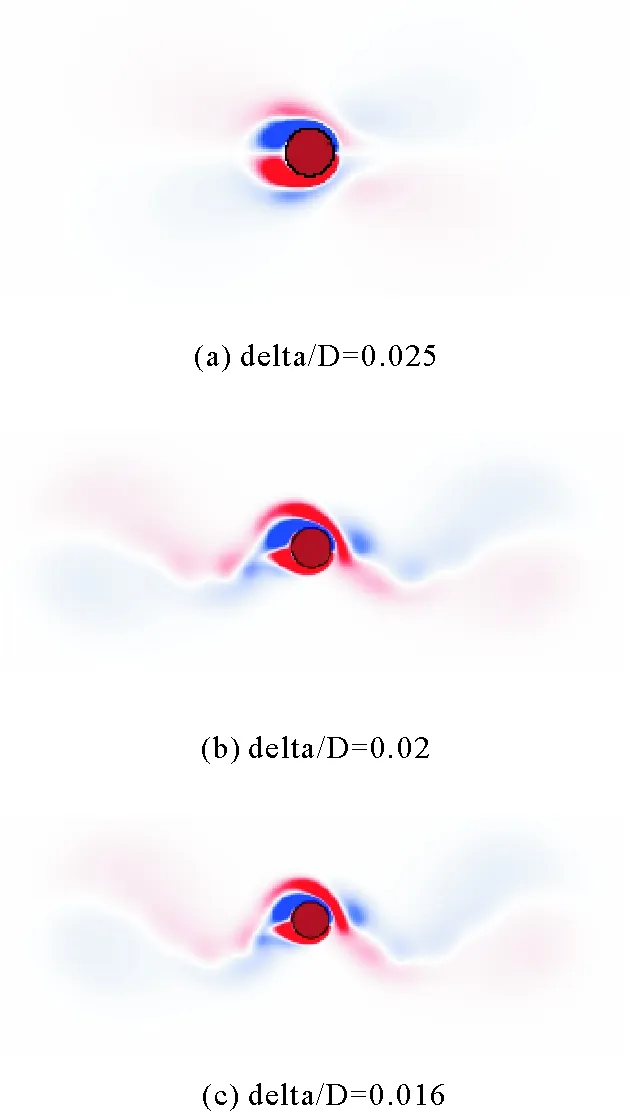
圖11 在KC=6時間為65時，不同網格的渦旋場的比較Fig.11 Comparison of vortices in different grids when KC=6, non-dimensional time=65

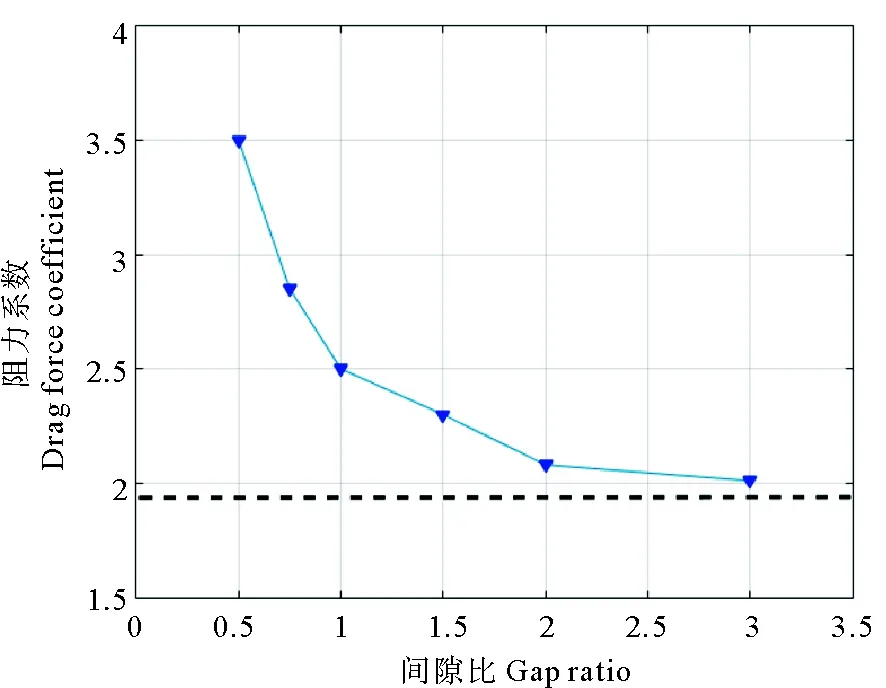
圖12 KC=6時的阻力系數CdFig.12 Drag Coefficient (KC=6)

可見，振蕩并列圓柱的阻力系數Cd比單圓柱的較大，隨著間隙比的增大，阻力系數Cd單調減小，并趨近于單圓柱的阻力系數。這與實驗結果的趨勢一致。

4 數值模擬的流場分析

4.1 振蕩雙圓柱流場

圖13給出了間隙比為0.5振蕩雙圓柱繞流在一個周期內的4個特征時刻的流場，在這4個時刻圓柱的運動狀態分別表示左側最大位移處(定義相位為0)，向右通過平衡位置處(定義相位為π/2)，右側最大位移處(定義相位為π)，向右通過平衡位置處(定義相位為3π/2)，以此描述一個運動周期內的流場變化。圖13(a)是圓柱運動到最左側位置(相位為0)時的流場，此時圓柱泄出渦對A和B，A的下部渦流(藍色的逆時針漩渦)和B的上部渦流(紅色的順時針漩渦)攜帶了大量能量。并在間隙中產生強相互作用，形成強噴射流X，快速遠離圓柱，其速度超過了圓柱的振蕩速度。當圓柱移動到右側最大位移時，如圖13(c)所示，渦對C和D泄出，與A和B類似，C的下部渦流和D的上部渦流在間隙中形成了新的渦流對Y。與X類似，Y攜帶了大量能量并快速遠離圓柱。同時圓柱激發了新的渦流對E與F。隨后，如圖13(d)所示，此后圓柱將運動到左側最大位移處，間隙中產生新的射流渦對。這些攜帶能量且具有較快速度的渦對，是雙圓柱系統阻力系數增大的原因。

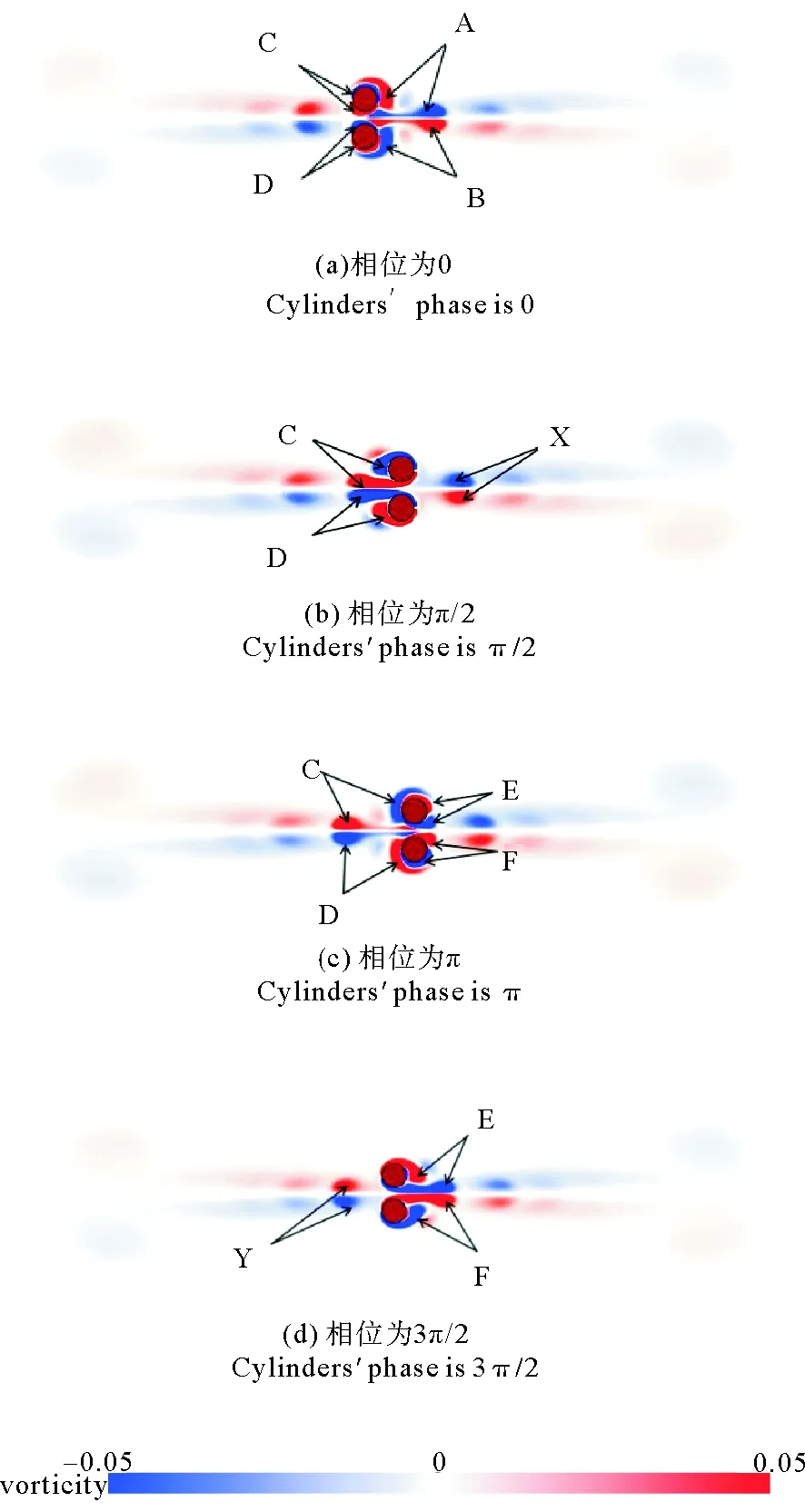
圖13 雙圓柱的流場發展 (KC數為6, 間隙比為0.5)

5.2 平均能量流出率

為了從能量角度定量的解釋雙圓柱系統阻力系數增大的現象，本文引入平均能量流出率(Mean Energy Outflow Rate，簡稱)，其定義式為：

其中：u為無量綱流體速度，其方向是控制體的外法線方向；ds是控制體的無量綱的單位邊長，控制體設置示意圖見圖10。平均能量流出率的物理含義是指：一個完整的振蕩周期中，選定控制體在單位時間內能量的流出，其大小體現了該情況下由于圓柱振蕩而流出的能量多少。選取KC數等于6的情況，對不同間隙比下的雙圓柱系統求得平均能量流出率(控制體內包含圓柱體)，如圖14所示，其中水平虛線表示振蕩單圓柱工況的平均能量流出率。

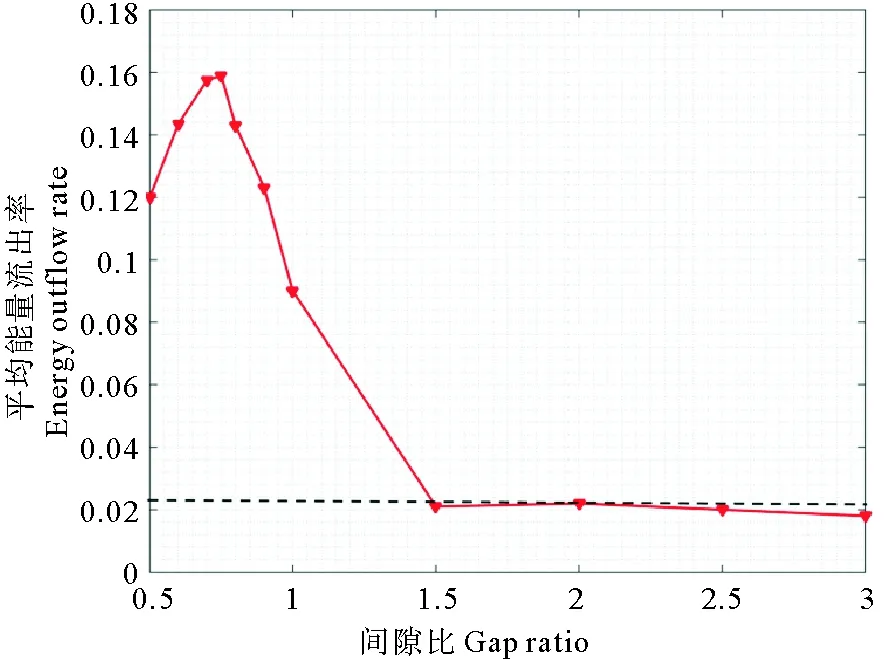
圖14 KC數等于6時不同 間隙比下圓柱求得平均能量流出率Fig.14 Energy outflow rate of cylinder with different gap ratio(KC=6)

因為平均能量流出率是對圓柱相對于水的相對速度進行邊界積分，而相對速度的大小影響了莫里森公式中的阻力，系數Cd，因此平均能量流出率隨間隙比的變化從能量的角度解釋了小間隙比條件下阻力系數Cd增大的機制。

5 結語

本文對做正弦式往復振蕩的并列雙圓柱系統在靜止流場里的水動力性能進行了實驗和數值模擬。實驗發現，小間隙比并列振蕩的情況與單個圓柱相比，阻力系數Cd在KC數>5時出現明顯的增大現象，附加質量系數Cm在小KC數下提前趨于穩定，升力系數Cl的方均根增大，而且Cl在小KC數下提前出現二階頻率分量。隨后，使用基于BDIM的數值模擬，針對KC數為6，β數為20(Re=120)的情況進行水動力學載荷計算和流場分析。數值模擬通過使用delta/D=50的網格，發現雙圓柱系統在小間隙比下并列振蕩時，由于兩圓柱流場之間的相互作用，在間隙中會產生間隙流和攜帶能量的渦流。通過計算各系統中流出的能量，研究發現小間隙比下雙圓柱系統產生的渦流攜帶的能量高于單圓柱系統，這一攜帶更多能量的渦流導致了小間隙比下雙圓柱系統阻力系數Cd的增大，而較大間隙比下雙圓柱之間的作用比較微弱，流出的能量也接近與單圓柱振蕩流出的能量。