差分進化神經網絡干擾觀測器的設計
孫明
(江南大學 物聯網工程學院,江蘇 無錫 214122)
干擾在控制系統中廣泛存在,加大控制難度,會給系統性能帶來不利影響,甚至會影響系統的穩定性。摩擦、測量噪聲、匹配/未匹配的不確定性、被控對象參數攝動等均會導致控制系統實際的性能或輸出偏離期望值,使系統控制效果和精度下降。因此,探尋觀測或估計干擾的有效方法,從而抑制或消除擾動成為控制領域的一大熱點。RBF神經網絡是具有單隱層的3層前饋網絡,能以任意精度逼近任意連續非線性函數,且其輸入層到隱含層的作用函數是高斯基函數,而隱含層到輸出層的映射是線性關系,所以RBF神經網絡具有較強的局部逼近能力,在避免局部出現極小值的情況下,兼具加快學習速度的作用,適合對干擾實時估計,滿足了系統快速性及自適應性的要求[1]。
文獻[2-7]取關于高斯基函數有關的神經網絡權值自適應率,得到對外部干擾、模型精確度不足、子系統交叉耦合和內部不確定性組成的復合干擾的逼近,用于設計控制器有關項,可提高系統魯棒性。自適應率的選取需保證各參數有界,干擾觀測誤差動態方程特征值趨于無窮大難以實現,導致估計誤差收斂范圍大于RBF神經網絡最佳逼近上界。差分進化(DE)算法通過對父代間差分矢量進行變異、交叉和選擇操作,篩選出適應度值更高的新個體,經過有限次迭代運算,優勝劣汰,得到被控對象目標函數的參數最優解[8]。本文結合文獻[3]和文獻[7],采用DE算法以動態方程估計誤差為適應度及最小化目標函數,對神經網絡權值在線全局優化,將全局極值作為干擾觀測器參數,用于逼近等效干擾。仿真結果表明: 該方法顯著簡化了觀測器的設計過程,有效地減小了估計誤差。
1 神經網絡干擾觀測器設計
針對如下一類n階不確定非線性系統:
(1)
式中:xi∈R——系統可測狀態,i=1, 2, …,n;f(x),g(x)——非線性函數;Δf(x), Δg(x),d(t)——分別為匹配或未匹配不確定性、參數攝動、外界干擾;u∈R——控制輸入。
整理式(1)中第二個式子可得:
(2)
對于任意x∈M,M為1個閉集區域,定義RBF神經網絡最優權值為
(3)

RBF神經網絡對等效干擾的逼近為
(4)
D(x,t)=ω*Tφ(x)+ε(x)
(5)

設計如下有關被控系統狀態的動態觀測方程:

(6)
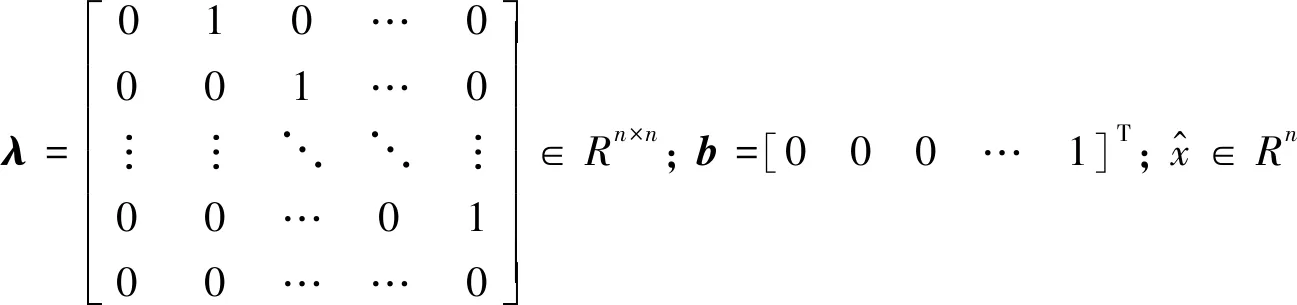

(7)
2 基于神經網絡的DE算法設計
DE算法的基本設計思路: 隨機產生1個初始種群,按照一定規則,將其中任意2個個體的向量差加權與某選定個體進行變異運算,根據目標函數確定適應度值,通過將新個體與該種群個體比較,淘汰適應度值更低的個體,經過有限次更新迭代,搜索全局最優解。上述步驟可概括為: 種群初始化、變異、交叉、選擇操作。
1) 初始化設置。采用式(8)對種群初始化,生成N個個體:

(8)

2) 變異。取種群中任意3個個體xr1,xr2,xr3;其中r1,r2,r3∈{1, 2, …,N}表示種群個體序數,且r1≠r2≠r3≠i。通過式(9)生成變異個體:
hi(k+1)=xr1(k)+F[xr2(k)-xr3(k)]
(9)
式中:xr2(k)-xr3(k)——差異化向量;F——變異比例因子;k——當前更新迭代次數。變異操作是差分進化算法核心,F的選取影響種群多樣性及收斂性,通常F取值為0.2~0.8,最大迭代次數不超過500。
3) 交叉。根據隨機概率將種群個體xi與其變異個體hi二項交叉生成新個體:
(10)
式中:rand——U[0,1];CR——交叉概率因子,取值為(0.5, 0.9)。
4) 選擇。以最小化問題min{f(x),x∈ψ}為例,其中ψ為D維非空有界閉集。將目標函數取為適應度函數,對xi(k)及實驗個體ui(k+1)進行適應度值評價,采用如下方法決定兩者之一成為下一代成員:
(11)
重復步驟2)至步驟4),直到尋優達到最大迭代次數或滿足評價值期望精度[9-10]。
3 仿真實驗
針對如下倒立擺系統:
(12)
(13)
(14)

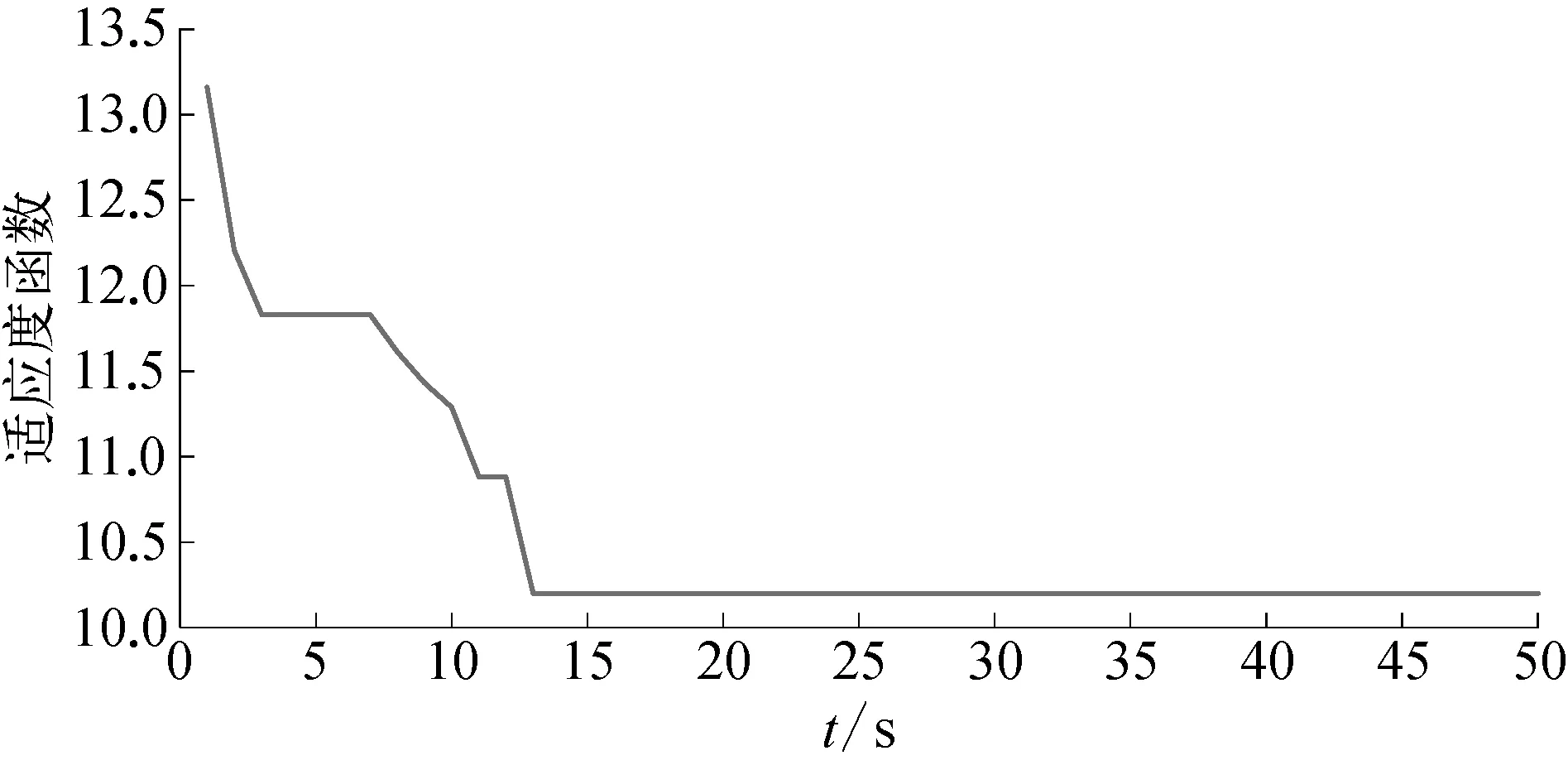
圖1 適應度函數迭代變化曲線示意

圖2 神經網絡權值變化曲線示意
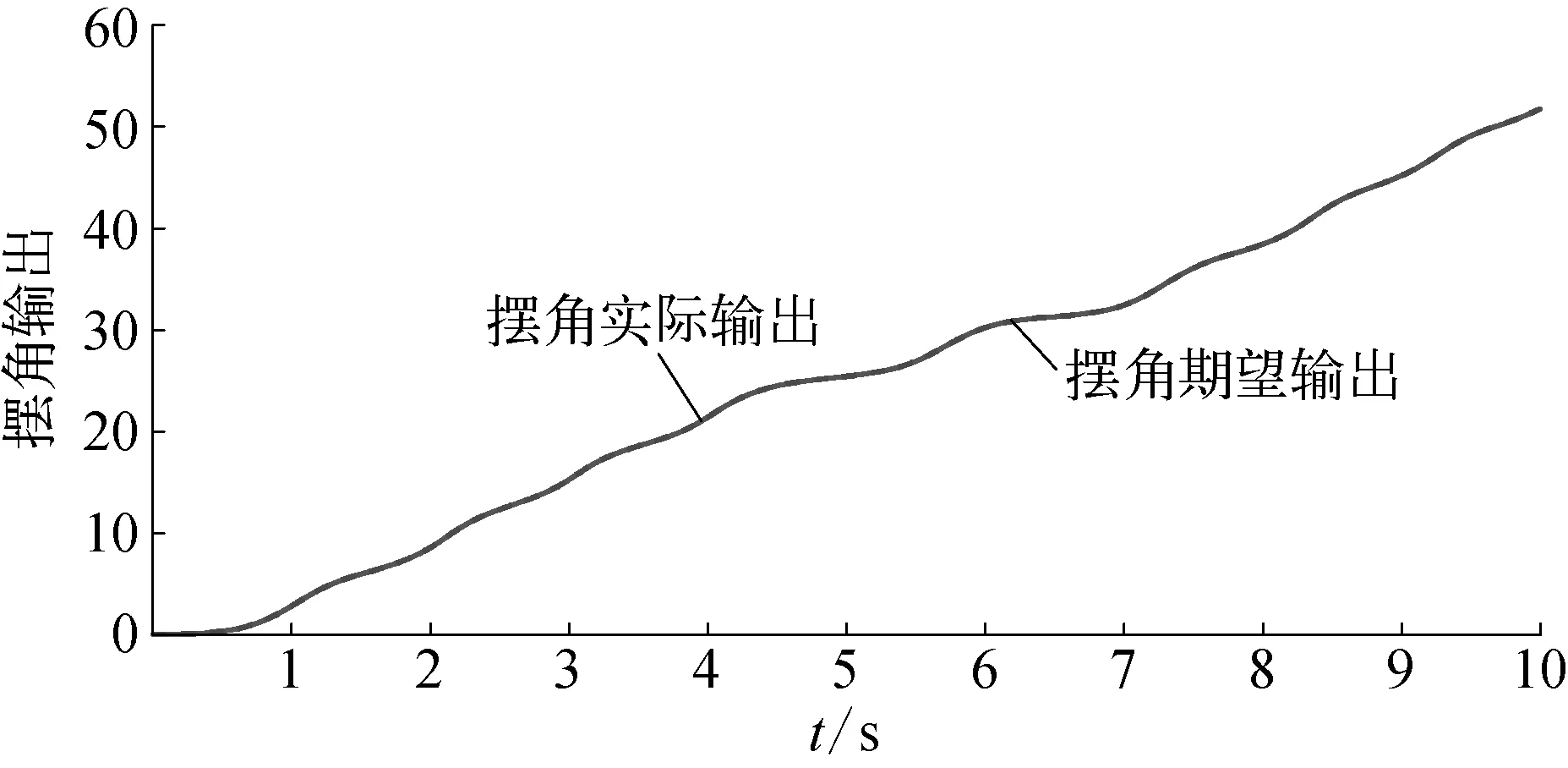
圖3 擺角實際輸出與期望輸出示意

圖4 擺角跟蹤誤差示意

圖5 擺角速度實際輸出與期望輸出示意

圖6 擺角速度跟蹤誤差示意

圖7 最優權值下的干擾估計示意

圖8 最優權值下的估計誤差示意
由圖1~圖2可知,迭代達到23次左右時,目標函數已達最小,種群尋得全局最優,神經網絡各權值獲得理想參數值。從圖3~圖6可看出,被控對象狀態動態觀測系統能精確逼近擺角及擺角速度變化,各逼近誤差較小。圖7與圖8為最優權值下神經網絡干擾觀測器對復合干擾的估計情況,與文獻[2]和文獻[5]采用自適應率動態調整網絡權值相比,引入DE算法的神經網絡對綜合干擾估計誤差得到有效減小。
4 結束語
本文針對不確定非線性系統,基于神經網絡設計非線性干擾觀測器,以被控對象狀態動態觀測系統對狀態逼近最小化為目標函數,采用DE算法通過初始化種群及變異、交叉、選擇操作運算后在線動態調整神經網絡輸出權值,將最優參數用于觀測器估計干擾。仿真結果表明: 差分進化神經網絡干擾觀測器能以較高精度逼近外界干擾,有效地避免了參數設置和整定的盲目性,對被控對象參數攝動具有較高的抗擾能力,對于實際工程系統設計具有重大指導意義。

