空爆下強(qiáng)力甲板損傷變形后艙段剩余極限強(qiáng)度分析

許皓然，張世聯(lián)，李 聰

（1. 上海交通大學(xué) 船舶海洋與建筑工程學(xué)院，上海 200240；2. 中國(guó)船舶及海洋工程設(shè)計(jì)研究院，上海 200011）

0 引 言

提升船體結(jié)構(gòu)的抗損傷能力、延長(zhǎng)艦船的使用壽命一直是各國(guó)海軍研究的重點(diǎn)。研究結(jié)果表明，在強(qiáng)力甲板下方合適位置處設(shè)置縱向箱型梁的結(jié)構(gòu)形式可有效抵抗爆炸和彈片帶來(lái)的損傷，保證艦船的縱向強(qiáng)度[1]。國(guó)內(nèi)外已有諸多學(xué)者對(duì)該結(jié)構(gòu)形式進(jìn)行探究。彭大煒等[2]通過(guò)計(jì)算分析發(fā)現(xiàn)，強(qiáng)力甲板損傷之后，設(shè)置縱向箱型梁的船體結(jié)構(gòu)的總縱極限承載能力要明顯強(qiáng)于普通船體結(jié)構(gòu)。王佳穎等[3]通過(guò)計(jì)算普通艙段與含縱向箱型梁艙段在外部非接觸式爆炸載荷作用下的結(jié)構(gòu)響應(yīng)發(fā)現(xiàn)，含縱向箱型梁的艙段結(jié)構(gòu)具有變形小、變形后艦體極限承載能力下降小等優(yōu)勢(shì)。

上述研究都是基于整體艙段模型的變形特征進(jìn)行的，強(qiáng)力甲板作為船體梁在中垂?fàn)顟B(tài)下承壓的主要構(gòu)件，一旦因爆炸而受到損傷，會(huì)對(duì)船體的剩余極限強(qiáng)度產(chǎn)生較大影響。由于剩余極限強(qiáng)度是衡量艦船生命力的重要指標(biāo)之一[4]，因此相關(guān)研究備受關(guān)注。

本文利用非線性有限元軟件ABAQUS研究強(qiáng)力甲板在空中爆炸沖擊載荷作用下的損傷變形對(duì)船體梁剩余極限強(qiáng)度的影響規(guī)律，并對(duì)比分析縱向箱型梁結(jié)構(gòu)對(duì)提高船體梁剩余極限強(qiáng)度的作用。

1 有限元計(jì)算模型

1.1 幾何特征

以某布置有3層甲板和雙層底的典型三艙段模型為研究對(duì)象，分別建立普通艙段模型（以下簡(jiǎn)稱模型A）和在強(qiáng)力甲板下設(shè)置3根縱向箱型梁的艙段模型（以下簡(jiǎn)稱模型B）。艙段全長(zhǎng)40.5m，型深12m，型寬17m，肋距0.5m，每隔3個(gè)肋位設(shè)置一道強(qiáng)肋骨框架，由2個(gè)橫艙壁分隔為3段等長(zhǎng)的艙段。模型B在模型A的基礎(chǔ)上，在強(qiáng)力甲板下方與左右舷連接處和船中處增設(shè)3根縱向箱型梁；考慮到總布置對(duì)層高的限制，船中處箱型梁的高度比兩側(cè)箱型梁的高度小。模型A和模型B典型橫剖面圖和局部有限元計(jì)算模型見(jiàn)圖1。

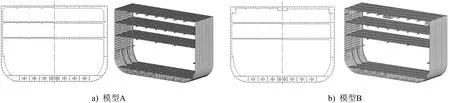
圖 1 模型A和模型B典型橫剖面圖和局部有限元計(jì)算模型

1.2 材料參數(shù)

研究對(duì)象的結(jié)構(gòu)材料為Q345鋼，其楊氏模量E=210GPa，泊松比μ=0.3，密度ρ=7.8×103kg/m3，彈性屈服應(yīng)力為345MPa。

在對(duì)爆炸性能進(jìn)行仿真計(jì)算時(shí)，材料本構(gòu)方程選用Johnson-Cook模型[5]，即

式(1)中：yσ為材料的塑性應(yīng)力；pε為等效塑性應(yīng)變；ε˙0ε˙為相對(duì)應(yīng)變率。

根據(jù)試驗(yàn)數(shù)據(jù)得到擬合參數(shù)：A=374MPa；B=795.71279MPa；C=0.01586；n=0.45451。

1.3 邊界條件

基于平斷面假設(shè)，在艙段首尾端面彎曲中心處設(shè)立獨(dú)立參考點(diǎn)P1和P2，通過(guò)模型預(yù)測(cè)控制仿真軟件（Model Predictive Control, MPC）將艙段端面上所有連續(xù)縱向構(gòu)件的節(jié)點(diǎn)自由度關(guān)聯(lián)到獨(dú)立參考點(diǎn)P1和P2，參考相關(guān)船級(jí)社規(guī)范的要求，邊界條件定義如下。

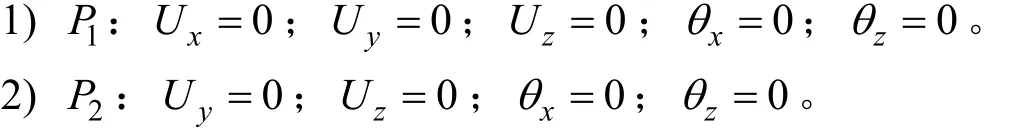
陸鼎等[6]通過(guò)研究發(fā)現(xiàn)，在求解空中爆炸問(wèn)題時(shí)，舷外水對(duì)艙段結(jié)構(gòu)抗爆響應(yīng)的影響不能忽略，因此將舷外水對(duì)船體的作用簡(jiǎn)化為水彈簧對(duì)船體的約束，施加于外板與強(qiáng)框架相交處的節(jié)點(diǎn)上。水彈簧剛度的計(jì)算式為

式(2)中：K為水彈簧的剛度；S為船體水線面面積；g為重力加速度；ρ為水的密度。

計(jì)算得到水彈簧的總剛度為6750N/mm，將這部分剛度平均分配到艙段外板與強(qiáng)框架相連接的節(jié)點(diǎn)上，每個(gè)節(jié)點(diǎn)分配到的剛度為3.04N/mm。

在求解極限載荷階段，在P1和P2上施加大小相等、方向相反的垂向彎矩，并依據(jù)一定的步長(zhǎng)逐步增大，以計(jì)算艙段的極限承載能力。

1.4 爆炸模擬

常用的模擬爆炸對(duì)結(jié)構(gòu)的沖擊作用的數(shù)值計(jì)算方法有流固耦合算法和CONWEP算法，其中：流固耦合算法能準(zhǔn)確地描述沖擊波的傳播過(guò)程及其與結(jié)構(gòu)之間的相互作用，但計(jì)算時(shí)間較長(zhǎng)；CONWEP算法認(rèn)為空氣中的爆炸會(huì)形成一團(tuán)與周圍空氣相互作用的高度壓縮的氣體，在壓力梯度的作用下形成一個(gè)向外傳播的球形沖擊波。在給定炸藥的TNT當(dāng)量和炸點(diǎn)位置之后，基于內(nèi)置的大量試驗(yàn)數(shù)據(jù)，CONWEP算法會(huì)自動(dòng)對(duì)爆炸工況進(jìn)行模擬計(jì)算。

喬遲[7]研究發(fā)現(xiàn)，CONWEP算法在計(jì)算速度上比流固耦合算法有顯著提升，對(duì)于不存在沖擊波與結(jié)構(gòu)反復(fù)發(fā)生作用的開(kāi)放式爆炸，可保證較高的精度。因此，本文采用ABAQUS中的CONWEP模塊來(lái)模擬仿真空中爆炸載荷，爆炸沖擊波壓力時(shí)歷曲線[8]見(jiàn)圖2。

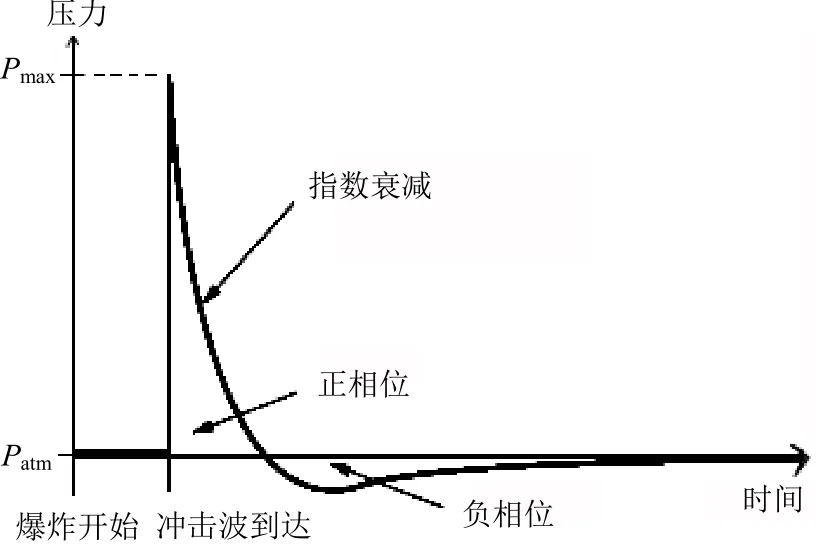
圖2 爆炸沖擊波壓力時(shí)歷曲線

1.5 爆炸工況

為模擬艦船受到爆炸沖擊之后造成的強(qiáng)力甲板損傷，合理設(shè)計(jì)爆炸工況十分重要。由于影響空中爆炸對(duì)目標(biāo)的破壞作用的主要因素是裝藥量W和爆炸點(diǎn)與目標(biāo)之間的距離R[9]，因此爆炸工況主要考慮這2個(gè)因素。在本文的爆炸仿真模擬中，裝藥量W分別選取 50kg、100kg、200kg、400kg、600kg 和 800kg。

當(dāng)爆炸點(diǎn)在船中處時(shí)，由于強(qiáng)力甲板遠(yuǎn)離舷側(cè)與艙壁結(jié)構(gòu)的支撐，該工況最為危險(xiǎn)，選擇爆炸位置沿船長(zhǎng)和船寬方向都位于艙段正中處進(jìn)行分析，沿高度方向分別選取Z=1m、2m、4m、6m、8m和12m。為方便表示，將爆炸工況記為“工況W–Z”，并將結(jié)構(gòu)模型在該工況下的計(jì)算結(jié)果記為MW–Z（例如：“工況200-6”表示W(wǎng)=200kg、Z=6m爆炸工況；MB200-6表示設(shè)置縱向箱型梁加強(qiáng)之后的結(jié)構(gòu)在該工況下的計(jì)算結(jié)果）。

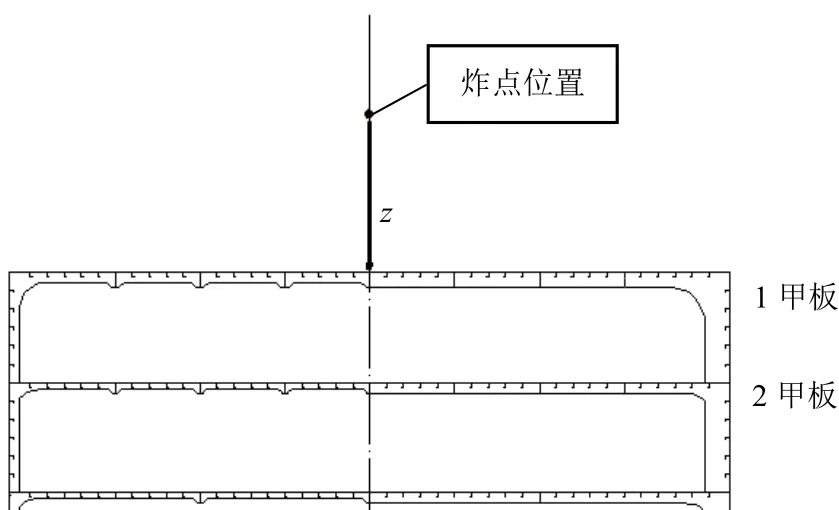
圖3 空中爆炸裝藥工況示意

2 強(qiáng)力甲板損傷變形

2.1 強(qiáng)力甲板損傷變形分析

在采用CONWEP算法對(duì)艙段施加爆炸沖擊載荷之后，得到強(qiáng)力甲板損傷變形之后的艙段模型（見(jiàn)圖4）。

為分析強(qiáng)力甲板損傷變形與艙段剩余極限強(qiáng)度之間的關(guān)系，首先需定義描述強(qiáng)力甲板損傷變形的參數(shù)。當(dāng)爆炸點(diǎn)在船中時(shí)，由于艙段模型和爆炸沖擊載荷的對(duì)稱性，損傷變形的強(qiáng)力甲板作為對(duì)稱結(jié)構(gòu)在對(duì)稱載荷下的響應(yīng)也具有相應(yīng)的對(duì)稱性；同時(shí)，強(qiáng)力甲板在艙中心點(diǎn)處的位移最大，當(dāng)艙段處于中垂?fàn)顟B(tài)時(shí)，強(qiáng)力甲板除了承受總縱彎曲應(yīng)力以外，還會(huì)承受爆炸沖擊波引起的甲板板架彎曲應(yīng)力。在艙段逐步崩潰過(guò)程中，艙段中心處的應(yīng)力水平最高，最先崩潰。因此，截取艙段受到爆炸沖擊之后的艙中處剖面進(jìn)行分析。圖5為模型B在受到工況800-6爆炸沖擊之后的艙中處橫剖面變形示意。

圖4 2種爆炸工況下的艙段變形模型

2.2 強(qiáng)力甲板損傷變形參數(shù)

強(qiáng)力甲板在近場(chǎng)和遠(yuǎn)場(chǎng)爆炸工況下會(huì)出現(xiàn)不同的損傷變形特征，當(dāng)爆炸點(diǎn)距離強(qiáng)力甲板較近時(shí)（如圖4a)所示）會(huì)出現(xiàn)破口，因此需找到能描述不同爆炸工況下強(qiáng)力甲板損傷變形特征的參數(shù)。

CZUJKO等[10]通過(guò)對(duì)一塊變形板架不同位置處進(jìn)行變形值的測(cè)量，發(fā)現(xiàn)可用傅里葉級(jí)數(shù)來(lái)描述板的變形。受此啟發(fā)，可使用三角函數(shù)級(jí)數(shù)來(lái)描述強(qiáng)力甲板受到爆炸沖擊之后在橫剖面上的變形。根據(jù)強(qiáng)力甲板損傷變形特征，采用第一階、第三階和第五階余弦函數(shù)來(lái)擬合損傷之后的強(qiáng)力甲板在艙中處橫剖面上的變形曲線，有

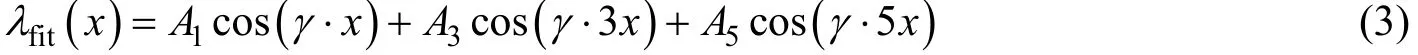
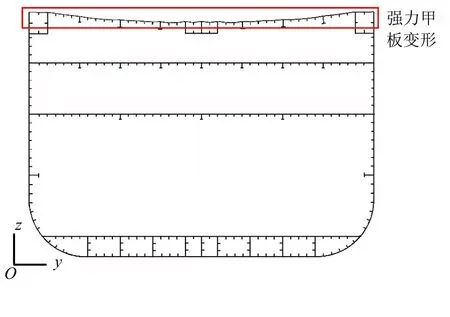
圖5 模型B在受到工況800-6爆炸沖擊載荷之后的艙中處橫剖面變形示意

式(3)中：A1、A3和A5為擬合系數(shù)；γ=π/l，l=17000mm為船寬，下同；x為強(qiáng)力甲板在橫剖面上的橫向坐標(biāo)，mm。

采用式(3)對(duì)2種工況下的強(qiáng)力甲板變形進(jìn)行擬合，結(jié)果見(jiàn)圖6。

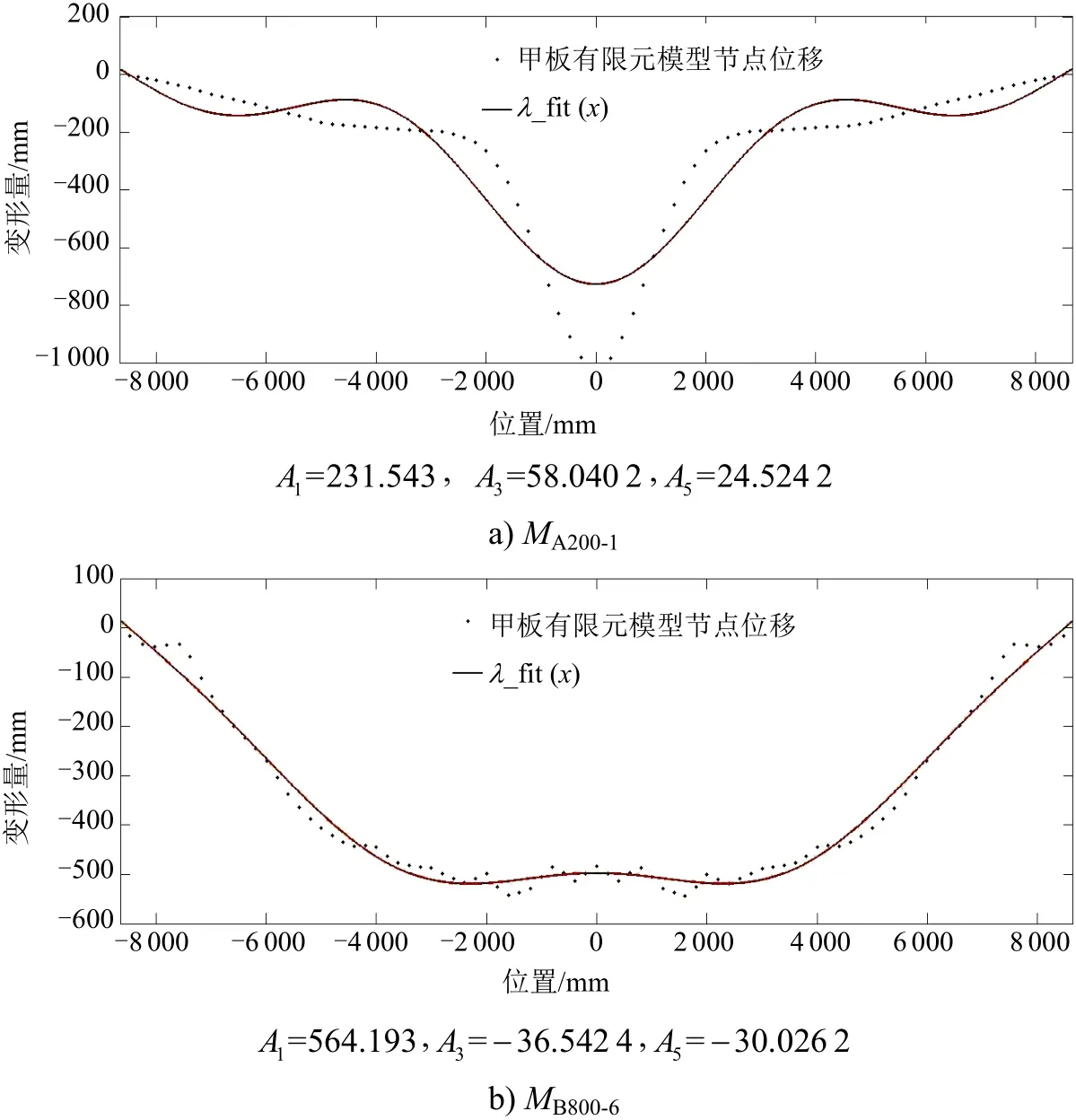
圖6 λ fit （ x）擬合結(jié)果

由圖6a)可知，由于出現(xiàn)破口（如圖4a)所示），爆炸點(diǎn)正下方破口處的變形值無(wú)法擬合，但對(duì)于破口周圍的擬合，仍可反映其變形特征，因此本文采用三角函數(shù)級(jí)數(shù)擬合。在得到描述強(qiáng)力甲板損傷變形的函數(shù)之后，通過(guò)式（4）計(jì)算定義變形均值λave作為描述強(qiáng)力甲板變形的參數(shù)，以此分析其與艙段剩余極限強(qiáng)度之間的關(guān)系，即

3 剩余極限強(qiáng)度

3.1 極限強(qiáng)度

在分析強(qiáng)力甲板損傷變形與艙段剩余極限強(qiáng)度之間的關(guān)系之前，首先計(jì)算得到2種模型在結(jié)構(gòu)完整狀態(tài)下的極限強(qiáng)度。一般在校核船體梁極限強(qiáng)度時(shí)，應(yīng)考慮“中拱”和“中垂”2種狀態(tài)，強(qiáng)力甲板作為船體梁在“中垂”狀態(tài)下的主要承壓構(gòu)件，當(dāng)受到損傷、具有大撓度變形時(shí)，會(huì)在很大程度上削弱整個(gè)船體在“中垂”狀態(tài)下的穩(wěn)定性，從而降低船體的總縱強(qiáng)度。因此，本文在分析艙段模型的極限強(qiáng)度時(shí)取“中垂”狀態(tài)。

在艙段兩端加載隨時(shí)間增大的強(qiáng)迫轉(zhuǎn)角θ，利用準(zhǔn)靜態(tài)法得到θ從0增大至0.05rad時(shí)作用在艙段模型兩端的彎矩。圖7為結(jié)構(gòu)完整狀態(tài)下2種模型的極限強(qiáng)度曲線，由圖中2條曲線近似線性變化階段的坐標(biāo)極值即可得到模型A和模型B在結(jié)構(gòu)完整狀態(tài)下的極限強(qiáng)度。對(duì)比2種模型的剖面面積和強(qiáng)力甲板處的剖面模數(shù)，結(jié)果見(jiàn)表1。

通過(guò)計(jì)算發(fā)現(xiàn)：模型B在“中垂”狀態(tài)下的極限彎矩比模型A高出20%；在甲板下設(shè)置縱向箱型梁對(duì)提升船體結(jié)構(gòu)的初始極限強(qiáng)度有一定的作用；在船體結(jié)構(gòu)后屈曲階段，模型B承載能力的下降趨勢(shì)比模型A緩慢。

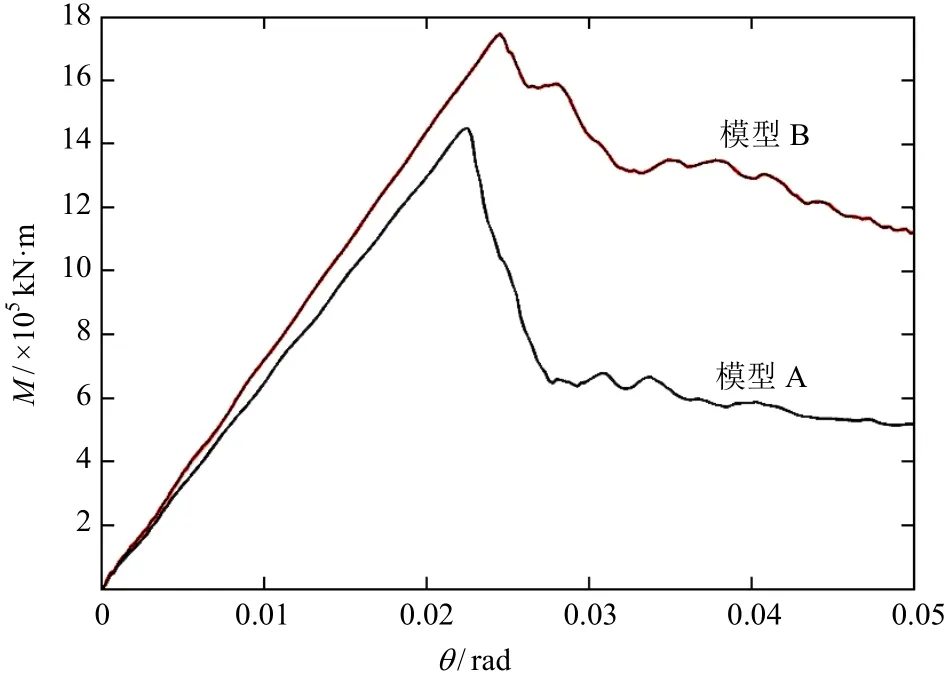
圖7 結(jié)構(gòu)完整狀態(tài)下2種模型的極限強(qiáng)度曲線

表1 完整結(jié)構(gòu)剖面參數(shù)和初始極限強(qiáng)度

3.2 剩余極限強(qiáng)度

以艙段受到爆炸沖擊之后出現(xiàn)最大變形瞬間的模型狀態(tài)作為初始位移條件，計(jì)算其在強(qiáng)力甲板發(fā)生損傷變形情況下的極限強(qiáng)度，即剩余極限強(qiáng)度Mr。由于2種結(jié)構(gòu)的極限強(qiáng)度明顯不同，為分析在爆炸沖擊載荷作用下不同艙段極限承載能力的降低程度，引入剩余極限強(qiáng)度能力保持因子Rf，有式(5)中：Mr為破損船體的剩余極限彎矩，kN·m；Mi為完整船體的極限彎矩，kN·m。

3.3 強(qiáng)力甲板損傷變形參數(shù)與剩余極限強(qiáng)度能力保持因子

通過(guò)分析強(qiáng)力甲板變形參數(shù)λave與相應(yīng)的艙段剩余極限強(qiáng)度能力保持因子Rf之間的關(guān)系發(fā)現(xiàn)，對(duì)于模型A，可用Farazdaghi-Harris曲線較好地表達(dá)其λave與Rf之間的關(guān)系，即

式(6)中：a、b和c均為常系數(shù)，a=1.00682，b=0.01107，c=0.74242。

圖8為模型A強(qiáng)力甲板變形均值與艙段剩余極限強(qiáng)度能力保持因子擬合曲線。由圖8可知：對(duì)于普通艙段結(jié)構(gòu)，隨著強(qiáng)力甲板在橫剖面上變形均值λave的增大，Rf呈下降趨勢(shì)，且在λave≤ 1 00 mm 范圍內(nèi)下降較快；隨著λave繼續(xù)增大，Rf下降趨勢(shì)逐漸減緩；當(dāng)λave≥ 4 00 mm 時(shí)，普通艙段結(jié)構(gòu)的Rf在0.4～0.5內(nèi)浮動(dòng)。

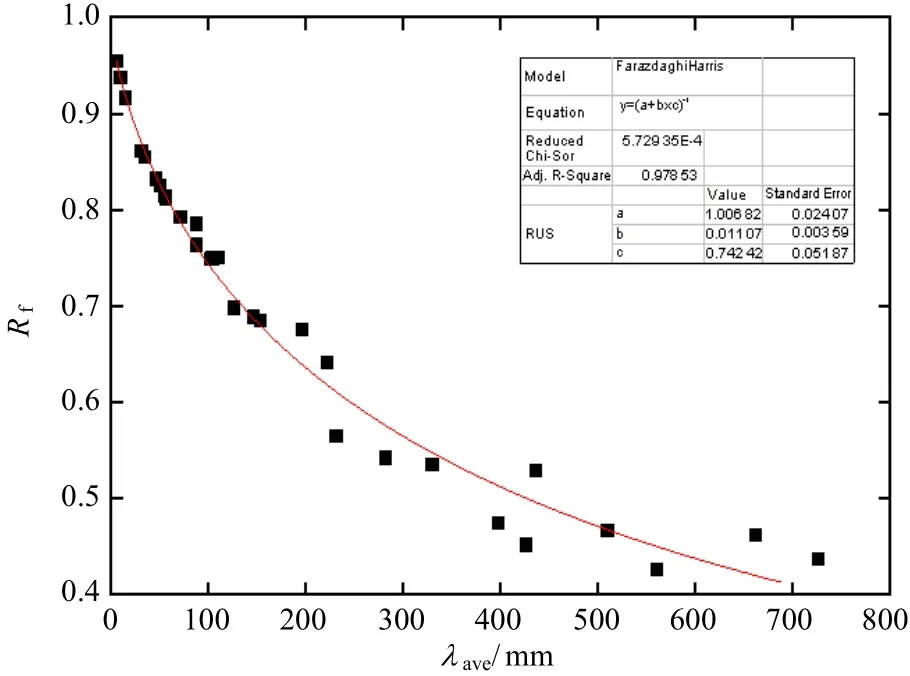
圖8 模型A強(qiáng)力甲板變形均值與艙段剩余極限強(qiáng)度能力保持因子擬合曲線

圖9 強(qiáng)力甲板各變形均值下艙段剩余極限強(qiáng)度 能力保持因子

圖9為強(qiáng)力甲板各變形均值下艙段剩余極限強(qiáng)度能力保持因子。為研究縱向箱型梁對(duì)強(qiáng)力甲板變形的影響，將圖9中的橫坐標(biāo)λave劃分為3個(gè)區(qū)間，在每個(gè)區(qū)間中選取一種爆炸工況，根據(jù)不同區(qū)間內(nèi)強(qiáng)力甲板在艙中處剖面上的變形曲線進(jìn)行討論：

1) 在區(qū)間Ⅰ（λave≤ 5 0 mm ）中，模型B和模型A在λave相等時(shí)Rf也大致相同。這主要原因?yàn)椋涸讦薬ve較小的情況下，整體損傷偏小，因此強(qiáng)力甲板板架依然具有較強(qiáng)的抗彎剛度，對(duì)2種結(jié)構(gòu)來(lái)說(shuō)都可作為縱向連續(xù)抗壓構(gòu)件；當(dāng)外部載荷逐步增大到極限彎矩時(shí)，在艙中處橫剖面上的大部分強(qiáng)力甲板構(gòu)件接近彈性屈服極限，因此2種模型的Rf相近。

2)在區(qū)間Ⅱ（ 5 0 mm＜λave≤ 2 50 mm）中，模型B的一個(gè)顯著特征是Rf不再隨著λave的增大而顯著減小，只是在0.80～0.85的“平臺(tái)”區(qū)間內(nèi)波動(dòng)。圖10為模型B在空爆載荷下的強(qiáng)力甲板變形曲線。由圖10b)可知，雖然該區(qū)間的強(qiáng)力甲板變形曲線與區(qū)間I（圖10a)）一樣呈“馬鞍”狀，但由于此時(shí)強(qiáng)力甲板整體變形較大，在船中縱向箱型梁左右兩側(cè)的甲板板架會(huì)有較大的剛度損失，使其無(wú)法繼續(xù)承載，而縱向箱型梁憑借其自身較強(qiáng)的面內(nèi)剛度，在爆炸沖擊載荷作用下變形撓度較小，依然具有良好的抗彎剛度。在該區(qū)間內(nèi)，λave的增大主要是由船中縱向箱型梁兩側(cè)甲板凹陷撓度進(jìn)一步增大引起的，由于該區(qū)域本來(lái)就已失去抗彎能力，因此對(duì)Rf的影響較小，這也就解釋了該區(qū)間內(nèi)“平臺(tái)”出現(xiàn)的原因。

圖10 模型B在不同空爆載荷下的強(qiáng)力甲板變形曲線

3) 在區(qū)間Ⅲ（λave＞ 2 50 mm ）中，在強(qiáng)烈的外部爆炸沖擊載荷作用下，強(qiáng)力甲板產(chǎn)生較大撓度的變形；同時(shí)，作為其支撐構(gòu)件的縱向箱型梁也具有很大的初始撓度。在這種情況下，包括箱型梁在內(nèi)的艙中區(qū)域的強(qiáng)力甲板幾乎完全喪失了板架平面內(nèi)的承壓剛度，極大地削弱了艙段的整體抗彎曲能力。只有舷側(cè)區(qū)域因受到箱型梁和舷側(cè)板架的支撐，且離爆炸點(diǎn)較遠(yuǎn)，還保留有一定的受壓承載能力。在該區(qū)間內(nèi)，λave表征強(qiáng)力甲板整體的大變形撓度，強(qiáng)力甲板的受壓承載能力損失會(huì)因λave的增大而增多，直到承載能力完全失去。因此，Rf表現(xiàn)為先減小后“水平”波動(dòng)的特征，這與普通艙段結(jié)構(gòu)的變化趨勢(shì)是一致的。

通過(guò)上述分析發(fā)現(xiàn)，當(dāng)強(qiáng)力甲板發(fā)生較大撓度的變形時(shí)（λave≥5 0 mm ），在強(qiáng)力甲板下合適的位置處設(shè)置縱向箱型梁可有效提高船體的剩余極限強(qiáng)度，對(duì)于目標(biāo)艦船而言可提高約15%。

4 結(jié) 語(yǔ)

通過(guò)上述計(jì)算分析，可得到以下結(jié)論：

1) 可用三角函數(shù)級(jí)數(shù)來(lái)擬合強(qiáng)力甲板受到爆炸沖擊之后在艙中橫剖面上的變形，以此描述強(qiáng)力甲板的損傷變形特征；

2) 普通艙段結(jié)構(gòu)遭受空中爆炸沖擊之后，剩余極限強(qiáng)度能力保持因子與強(qiáng)力甲板在艙中處橫剖面上的變形均值之間的關(guān)系可用Farazdaghi-Harris曲線較好地?cái)M合。

3) 當(dāng)強(qiáng)力甲板在空爆載荷下發(fā)生較大撓度變形時(shí)，在強(qiáng)力甲板下合適的位置處設(shè)置縱向箱型梁可有效提高船體的剩余極限強(qiáng)度。

【 參 考 文 獻(xiàn) 】

[1] 易基圣. 德國(guó)新一代F124級(jí)防空護(hù)衛(wèi)艦[J]. 國(guó)外艦船工程，1999 (3): 10-14

[2] 彭大煒，張世聯(lián). 兩種強(qiáng)力甲板結(jié)構(gòu)形式在大變形損傷狀態(tài)下的極限強(qiáng)度分析[J]. 艦船科學(xué)技術(shù)，2010, 32 (4): 15-18.

[3] 王佳穎，張世聯(lián)，彭大煒. 非接觸爆炸下縱向箱型梁艦船的極限承載能力研究[J]. 中國(guó)艦船研究，2011 (1): 22-29.

[4] 俞慶，張圣坤，沐陽(yáng). 基于余度概念的受損船體總縱剩余強(qiáng)度預(yù)報(bào)[J]. 中國(guó)造船，1996 (1): 30-38.

[5] 于文靜，史健勇，趙金城. Q345鋼材動(dòng)態(tài)力學(xué)性能研究[J]. 建筑結(jié)構(gòu)，2011 (3): 28-30.

[6] 陸鼎，張世聯(lián). 邊界約束對(duì)爆炸載荷作用下艙段結(jié)構(gòu)響應(yīng)的影響分析[J]. 艦船科學(xué)技術(shù)，2016, 38 (7): 28-32.

[7] 喬遲. 空中爆炸載荷下箱型梁防護(hù)結(jié)構(gòu)研究[D]. 上海：上海交通大學(xué)，2015.

[8] Abaqus Analysis User's Guide[DB/OL]. http://129.97.46.200:2080/v6.13/books/usb/default.Htm?startat=pt07ch34s04aus125.html#usb-prc-pacoustic

[9] 張寶平，張慶明，黃風(fēng)雷. 爆轟物理學(xué)[M]. 北京：兵器工業(yè)出版社，2001.

[10] CZUJKO J, KMIECIK M. Post welding distortions of ship shell plating[R]. Ship Research Institute, Technical University of Szceczin, 1975.