基于半張量積壓縮感知的形變數據重構在航天器結構健康監測中的應用

田引黎，楊林華，張鵬嵩，曹海林

（1. 重慶大學 微電子與通信工程學院，重慶 400030；2. 北京衛星環境工程研究所，北京 100094）

0 引言

近年來，航天器結構逐漸趨于大型化和復合材料化，對航天器性能的要求也逐漸提高，安全問題日益突出。航天器工作環境惡劣且難以維護，一旦發生事故，損失慘重，若能對航天器結構故障進行有效診斷，將會減少航天器飛行事故的發生。因此，實時監測航天器的結構健康狀況意義重大。結構健康監測（structural health monitoring, SHM）可以實時監測航天器健康狀況，及時提示對航天器的損傷進行維護，從而降低發生航天事故的風險。實時SHM主要是從傳感器采集大量數據，并提取能夠預測結構健康狀況的相關特征。隨著無線傳感網絡技術的發展，使得前端不間斷采集數據成為可能，然而大量數據的傳輸和存儲成為無線傳感網絡面臨的主要挑戰。因此，人們一直在探索新的方法，希望能減少數據的儲存和傳輸量，以減輕無線傳感網絡的儲存壓力，從而延長無線傳感網絡的生命周期。

傳統的數據壓縮方法采用先采樣后壓縮的方式，雖然可以減少傳輸數據的容量，但是并沒有減少采集數據的容量。針對這一不足，Donoho[1]提出了采集和壓縮同時進行的方法——壓縮感知（compressed sensing, CS），可大量節省信號采集占用的儲存空間。但CS的應用需要滿足2個條件：1）信號滿足某種特定的稀疏性；2）觀測矩陣滿足有限等距性[2]。實際上，大部分自然信號都是稀疏的或者在某種變換基下是稀疏的，因此CS技術一經提出即引起廣大研究者的興趣，被廣泛應用于智能電網、電子鼻等各個領域[3-4]。也有相關文獻將CS用于SHM：應用CS進行橋梁加速度信號的壓縮采樣[5]；應用CS對無線傳感器網絡進行數據修復[6]；應用CS對振動信號進行監測與診斷，以減小數據的存儲量[7]；將CS應用在Lamb波SHM中，以降低測量信號的存儲量[8]等。由于CS重構必須滿足有限等距性，而隨機矩陣具備優良的不相干特性[1]，所以隨機矩陣是目前CS應用的普適觀測矩陣。但隨機觀測矩陣在實際使用過程中，通常具有占用內存多、計算復雜度高等局限性。鑒于此，半張量積壓縮感知（semi-tensor product compressed sensing,STP-CS）方法[9]被提出，這是一種泛化的CS，突破了傳統CS矩陣相乘時的維數一致限制。

本文應用STP-CS技術，以航天器翼梁形變監測為例，首先采用離散余弦變換（DCT）對形變數據的稀疏性進行研究，然后利用降維的隨機高斯矩陣對形變數據進行壓縮采樣，最后通過正交匹配追蹤對采集的數據進行重構，驗證該方法的有效性。該方案旨在縮小觀測矩陣的存儲空間，為解決航天器SHM的儲存和傳輸量過大問題提供理論支持。

1 基于STP-CS的航天器形變數據壓縮采樣模型

以航天器形變數據為例說明STP-CS的算法流程。

設長度為n的航天器形變信號x∈Rn×1，通過STP-CS模型[10]

測量得到壓縮采樣后的航天器形變信號y∈Rm×1，其中Φ代表觀測矩陣。

如果航天器形變信號在時間域不具有稀疏性，可以通過變換域將其轉換成稀疏信號

其中：Ψ為變換矩陣；θ為稀疏矩陣。將式(2)代入式(1)可得：

當t=1時，式(3)即為傳統的CS模型。

2 航天器形變數據重構

CS重構一直以來都是研究的熱點，目前已經有很多成熟的重構方法，大體分為3類：1）凸優化方法，如l1范數，該類方法具有較強的重構性能，但是所需時間比較長；2）貪婪算法，如正交匹配追蹤，該類方法相比于凸優化算法，運算時間短，但是重構性能相對較弱；3）迭代閾值算法，該方法運算時間和重構性能都位于前二者之間。考慮到航天器SHM的實時性要求比較高，本文選擇正交匹配追蹤作為航天器形變數據重構的算法[9]。基于正交匹配追蹤重構的航天器形變數據算法流程如下：

1）輸入：壓縮采樣后的航天器形變數據為y∈Rm×1，傳感矩陣A∈Rm×n，迭代次數K。

3 實驗驗證

基于STP-CS的航天器結構監測系統形變數據的采集過程如圖1 所示，具體可以分為4步：

2）將采集到的航天器形變數據流ym×1進行無線傳輸；

3）在接收端即對接收到的數據ym×1進行重構，采用正交匹配追蹤算法恢復出變換域的稀疏數據；換，獲得重構后的航天器形變數據。

4）對變換域的航天器形變稀疏數據進行逆變

圖1 基于 STP-CS 的形變數據壓縮采樣及重構流程Fig. 1 Flow chart of deformation data compressed sampling and reconstruction based on STP-CS

3.1 基于離散余弦變換的稀疏變換

為了驗證該算法在航天器SHM中的可行性，本文選取航天器機翼形變信號作為研究對象，但由于獲取實測航天器機翼形變信號較難，本文以橋梁形變信號的撓度信號近似替代進行研究。航天器機翼形變指的是機翼與大氣相互作用產生升力時，通過翼梁將所承受的力傳遞給機體，在力的作用下機翼會發生一定的形變[11]。而橋梁結構形變指的是橋梁結構長期受到外界因素的影響會產生形變[12]。二者都是因為外界影響產生形變，當形變過大時，將會導致災難發生。因此，橋梁形變信號與航天器機翼形變信號具有一定的相似性。橋梁撓度是指橋之梁在載荷作用下不同位置處所產生的豎向變形[13]。本文選取了1024個橋梁撓度數據進行處理，如圖2所示。

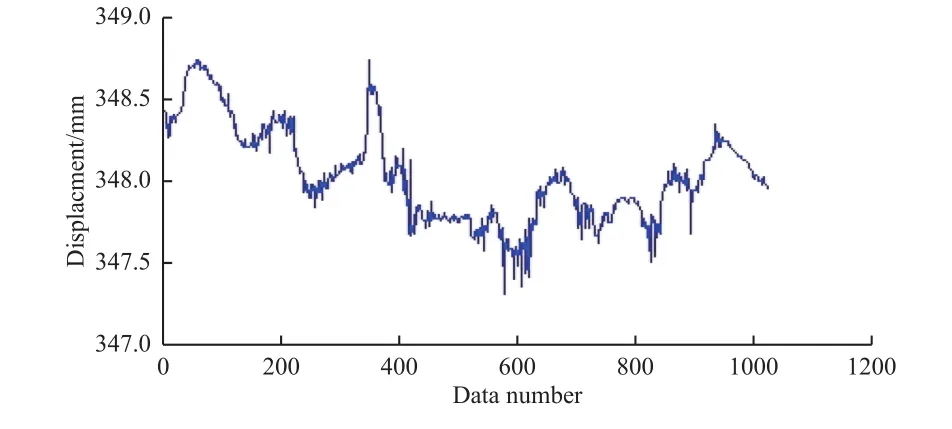
圖2 撓度信號Fig. 2 Deflection data

由圖2可知，撓度信號在時域并不稀疏，需要找到適合該信號的稀疏基，對其進行變換，使之在變換域是稀疏的。本文采用DCT對撓度信號進行變換，變換效果如圖3所示，可見變換后的撓度信號在DCT域具有稀疏性。

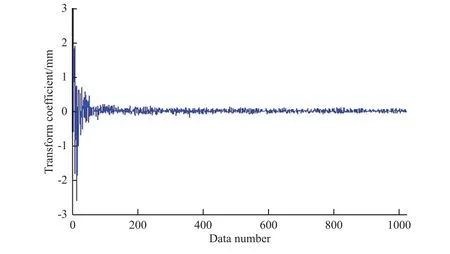
圖3 DCT 變換后的撓度信號Fig. 3 Deflection signal after DCT transformation

3.2 重構性能的評估

為了評估重構性能的優劣，本文采用相對誤差R作為衡量指標，

由于隨機矩陣具有良好的不相干性，本文選取隨機矩陣作為觀測矩陣。為了驗證STP-CS觀測矩陣的低儲存性，我們分別取觀測矩陣維數為傳統CS觀測矩陣維數的1、1/2、1/4、1/8倍，觀測矩陣儲存空間為傳統 CS觀測矩陣的 1、1/4、1/16、1/64，即t=1、2、4、8。當t=1時，該算法等同于傳統 CS。重構效果如圖4所示，可見隨著觀測矩陣維數的降低，即觀測矩陣存儲空間的減小，重構誤差有所增大，但并不明顯。

圖4 采用不同觀測矩陣維數時的信號重構效果Fig. 4 Signal reconstruction by using different observation matrix dimensions

圖5所示為基于STP-CS的形變數據重構的重構時間與觀測矩陣維數的關系，顯然隨著觀測矩陣維數的降低，重構時間也在不斷縮短。

圖5 采用不同觀測矩陣維數時的重構時間Fig. 5 Reconstruction time in using different observation matrix dimensions

4 結束語

為了解決航天器SHM面臨的數據儲存和傳輸量過大問題，本文應用STP-CS模型進行采樣數據降維。實驗數據驗證結果表明：采用該方法在減小觀測矩陣儲存空間的同時仍能以較高精度重構壓縮采樣數據，而且隨著觀測矩陣維數的降低，重構時間也在不斷縮短；但隨著觀測矩陣維數的降低，重構誤差會有所增加，換言之，儲存空間和重構時間的減少是以增加重構誤差為代價的。如果在可接受的誤差范圍內采用該方法進行壓縮采樣及重構，可以有效減少采樣數據和傳輸數據量，縮減儲存空間和重構時間，提高航天器SHM的效率。