農用車柔性底盤姿態切換參數對切換精度與時間的影響及其優化
李翊寧,郭康權,2※,陳文強,瞿濟偉,高 華
?
農用車柔性底盤姿態切換參數對切換精度與時間的影響及其優化
李翊寧1,郭康權1,2※,陳文強3,瞿濟偉1,高 華1
(1. 西北農林科技大學機械與電子工程學院,楊凌 712100;2. 陜西省農業裝備工程技術研究中心,楊凌 712100;3. 第一越南蘇聯職業技術學院電子工程學院,福安市 15910)
為了研究農用車柔性底盤的姿態切換運行特性,該文進行了柔性底盤姿態切換分析和基于二代樣機在硬化路面上的姿態切換試驗,建立了姿態切換狀態模型,并通過層次分析法和遺傳算法優化了切換參數,研究了不同平移角度、電機轉速、切換角度、平移速度和回轉速度條件下的切換精度和切換時間,得到各因素及其交互作用對農用車柔性底盤姿態切換的影響和不同切換參數的相互配合關系。結果表明:影響準備與恢復精度的主次因素為電機轉速>平移角度,影響準備與恢復時間的主次因素為平移角度>電機轉速;橫行姿態的平移速度對其橫行精度和時間都有極顯著的影響,任意平移角度下,橫行姿態的電機最優轉速為5.4 r/min,最優平移速度為3.45 m/s;影響原地回轉姿態的回轉精度主次因素為:切換角度>回轉速度;影響原地回轉姿態的回轉時間主次因素為:切換角度>回轉速度>交互作用;任意平移角度下,原地回轉姿態的最優電機轉速為5.4 r/min,當切換角度為0~85°時,最優回轉速度為(0.003 3β+0.506 8) rad/s,當切換角度大于等于85°時,最優回轉速度為0.78 rad/s。優化參數對比結果表明:橫行姿態中,優化參數組的試驗結果在綜合精度方面與精度優先組持平并高出時間優先組4.16%,在綜合時間方面與時間優先組持平并少于精度優先組17 110 ms;原地回轉姿態中,優化參數組的試驗結果在綜合精度方面與精度優先組持平并高出時間優先組5.15%,在綜合時間方面分別少于時間優先組和精度優先組646和996 ms。優化后的姿態切換參數能夠保證柔性底盤在略微損失姿態切換精度的情況下,以較快的姿態切換效率完成其姿態切換過程。
農業機械;車輛;柔性底盤;姿態切換;參數優化;層次分析法;遺傳算法
0 引 言
中國設施農業對機械化與自動化要求迫切[1-3]。但是設施農業內的空間有限,傳統農用車輛底盤不能很好地適應設施農業內部以及復雜的道路環境。為此,很多科研人員在四輪獨立驅動與四輪獨立轉向農用車輛底盤方面進行了相關研究。張鐵民等[4-5]研制了四輪獨立驅動小車的電機驅動和四輪轉向控制系統,實現了不同負載和路況下穩定的運行。張京等[6]設計了基于低速阿克曼四輪轉向模型與PID控制算法的四輪獨立轉向驅動控制系統,分析并驗證了四輪獨立轉向驅動控制策略的有效性。Ko等[7]研制了用于溫室農業噴灑作業的移動機器人平臺,并從系統集成的角度研究了該機器人的自主駕駛策略。Oksanen等[8]對4WS遙控拖拉機的轉向結構與過程進行了建模,并針對四輪轉向提出了一種非線性補償控制 設計。
但是,以上各研究在完成了基本的車輛底盤研制與測試后,都把隨后的研究重點轉向了基于GNSS或機械視覺等用于底盤導航方面的內容,并沒有深入挖掘四輪獨立驅動與四輪獨立轉向技術對農用車輛底盤在轉向與角度轉換等方面的運行特點及其適用性,未能體現出此類新型底盤系統相對于傳統農用車輛底盤的優越性。
同時,本項目組在柔性底盤一代樣機及其試驗平臺的基礎上,進行了柔性底盤運動與動力學特性的測定[9-11],并完成了柔性底盤驅動與轉向協同控制特性試驗[12],對柔性底盤模式切換控制參數進行了相應優化[13]。但是,柔性底盤一代樣機為理論原型機,其結構特點、功率載荷和控制系統等都不適用于實際道路情況。并且一代樣機的測試與優化為試驗臺架上的理想環境,并不能完全反應底盤在實際運行過程中的特性。因此,項目組設計并研制了柔性底盤二代樣機[14],并對其在硬化路面上的平移模式與姿態切換模式之間的非連續轉換進行了相關研究。
本文主要探討柔性底盤在姿態切換模式中,底盤各切換參數對不同的切換姿態在準備、保持與恢復3個階段的優化問題。采用層次分析法確定各階段試驗指標的權重值,并通過遺傳算法對姿態切換狀態模型進行最優解的求解,得到底盤在姿態切換模式中各切換參數的最優配合關系,提高了柔性底盤在此運行過程中的穩定性和效率。
1 姿態切換模式分析
柔性底盤平移模式和姿態切換模式的轉換過程如圖1所示。柔性底盤的基本運行模式為平移模式。平移模式下,底盤直線運行方向與底盤坐標系的軸存在一個[0, 45°]的夾角,稱之為平移角度(°)。此時底盤整機和4個單輪行走系之間的運動關系如式(1)所示。
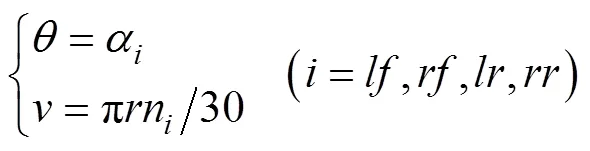
式中α為單輪行走系的偏置軸轉角,(°);為柔性底盤的平移速度,m/s;為輪胎半徑,m;n為單輪行走系的輪轂電機轉速,r/min;下標、、和分別表示左前、右前、左后和右后單輪行走系。
柔性底盤的姿態切換模式總是從平移模式轉換而來,并在姿態切換過程運行完成后,再次恢復為平移模式。柔性底盤的姿態切換模式分為橫行姿態和原地回轉姿態。2種切換姿態和平移模式之間的相互轉換過程總體一致,分為準備階段、保持階段和恢復階段。2種切換姿態在具體實現過程中存在差異,需要進一步分析。
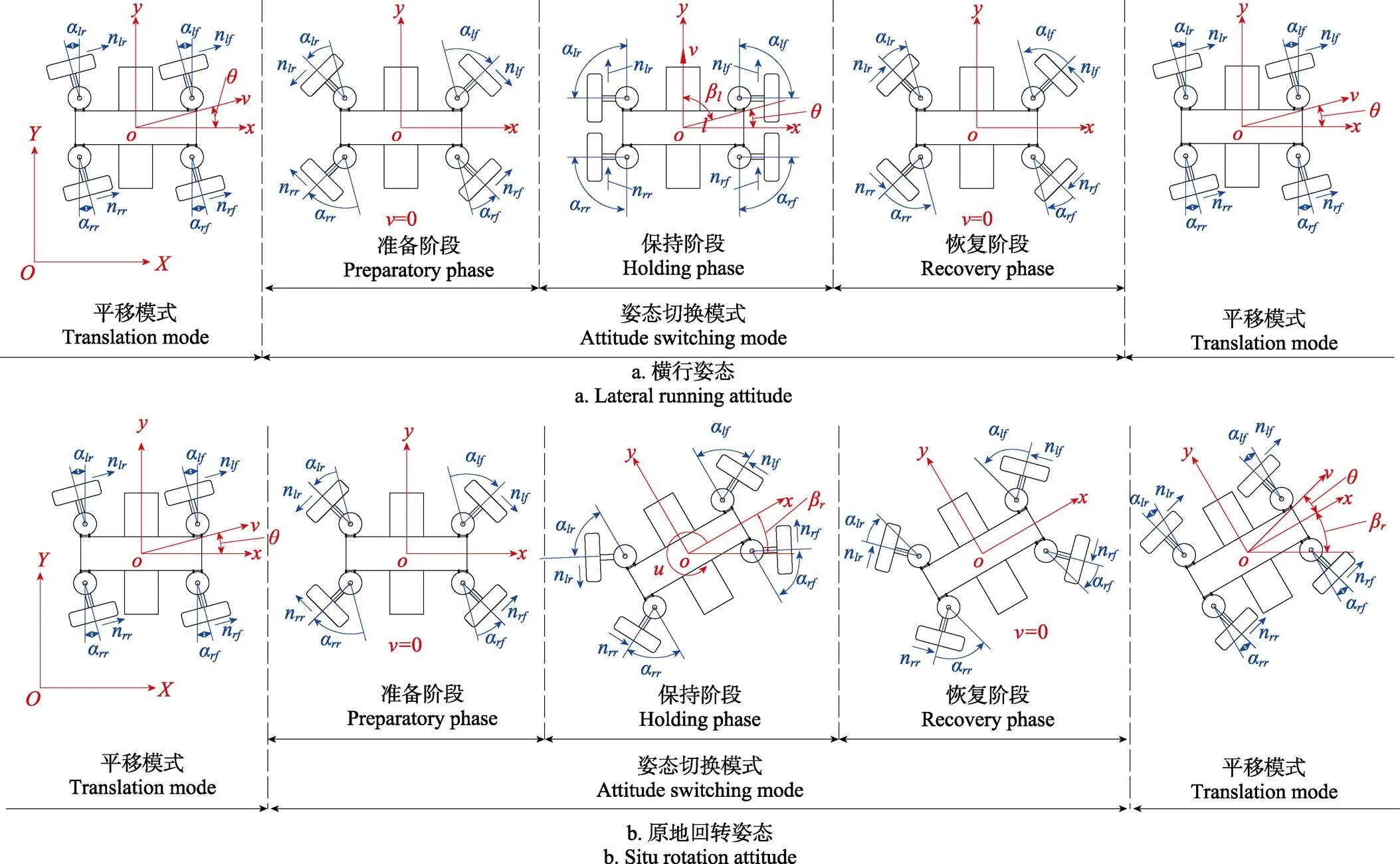
注:XOY為地面坐標系;xoy為底盤坐標系;v為底盤的平移速度,m·s–1;u為底盤的原地回轉速度,rad·s–1;βl為底盤在橫行姿態下的切換角度,(°);βr為底盤在原地回轉姿態下的切換角度,(°);θ為底盤的平移角度,(°);ni (i=lf, rf, lr, rr)為4個單輪行走系的電機轉速,r·min–1;αi (i=lf, rf, lr, rr)為4個單輪行走系的偏置軸轉角,(°);下標lf、rf、lr、rr分別表示左前、右前、左后和右后單輪行走系,下同。
1.1 準備階段
準備階段為柔性底盤由平移模式向姿態切換模式轉換的過程。橫行姿態和原地回轉姿態在此階段的運行方式是一致的,即底盤坐標系相對于地面坐標系保持不變,底盤的平移速度始終為0。但在柔性底盤內部,4個單輪行走系內的輪轂電機開始運行,并解除電磁鎖緊裝置對偏置軸位置的限定,使4個偏置軸轉角α借助輪胎與地面的摩擦力矩相互配合,以實現橫行姿態或原地回轉姿態所需的底盤狀態。設偏置軸轉角α繞各單輪行走系回轉中心逆時針為正。如圖1.a所示,當左前偏置軸轉角α達到–90°時,底盤切換為橫行姿態;如圖1b所示,當左前偏置軸轉角α達到–62.3°,底盤切換為原地回轉姿態。而其余各單輪行走系偏置軸轉角α的配合關系可依據底盤結構和姿態切換要求得出,具體如式(2)所示。
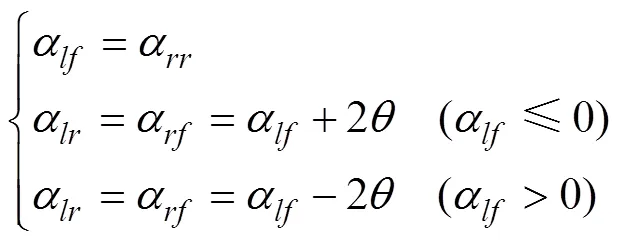
1.2 保持階段
保持階段為柔性底盤在橫行姿態或原地回轉姿態下保持固定運行狀態的過程。對于橫行姿態而言,柔性底盤以設定的平移速度做橫向直行,即底盤坐標系相對于地面坐標系僅有平移而無轉動,其切換角度β與平移角度互余。對于原地回轉姿態而言,柔性底盤繞其形心以設定的回轉速度原地轉動,即底盤坐標系相對于地面坐標系僅有轉動而無平移,其切換角度β為[–180°, 180°]內的任意值。此階段柔性底盤4個單輪行走系內的電磁鎖緊裝置一直處于工作狀態,保證4個偏置軸轉角α始終穩定在所需的固定值。
1.3 恢復階段
恢復階段為柔性底盤在完成所需的切換姿態運行后,重新向平移模式轉換的過程。其運行狀態和各項參數之間的關系都與準備階段保持一致而方向相反,即恢復階段與準備階段為互逆變化過程。由于2種切換姿態在保持階段的運行狀態不同,此階段結束后,對于橫行姿態,其底盤坐標系與地面坐標系之間無角度變化,底盤繼續以平移角度直線前行;而對于原地回轉姿態,底盤同樣以平移角度直線前行,但底盤坐標系與地面坐標系之間會存在切換角度β,因此其在地面坐標系內的直行方向會變為(+β)。
2 姿態切換試驗方案
由前述分析可知,柔性底盤的姿態切換過程較為復雜,包括了多個切換參數的變化與配合。其在準備與恢復階段主要為柔性底盤內部的4個單輪行走系偏置軸轉角α和輪轂電機轉速n的相互配合;而在保持階段主要為柔性底盤整機的橫向直行或原地回轉。
另外,從姿態切換3個階段的角度考慮,準備階段的運行效果必定會對保持階段的運行效果造成影響;而恢復階段則會受到準備與保持階段的共同作用,并對后續的底盤運行造成影響。
因此,需要根據柔性底盤在不同姿態切換階段中各種運動方式的共性與差異來設計分步試驗,以得到底盤采用不同切換姿態在各階段的運行規律。并通過分步試驗結果來優化底盤姿態切換的整個過程。
2.1 試驗因素與指標
由于底盤在姿態切換各階段運動的多樣性,在采用分步試驗時,其試驗因素與指標之間的關系也較為復雜,需要詳細說明。
2.1.1 試驗因素與水平
1)底盤的平移角度:依據柔性底盤結構與運行特性,底盤的平移角度在[0, 45°]內連續變化,并影響4個單輪行走系偏置軸轉角值和底盤切換角度范圍的大小。平移角度分為5水平,具體取0、15°、25°、35°和45°。
2)左前單輪行走系的電機轉速n:柔性底盤在準備與恢復階段中,應盡可能的降低4個單輪行走系中輪轂電機的轉速值,以保證4個單輪行走系偏置軸轉角相互配合的穩定性。通過試驗測定,輪轂電機的最低穩定轉速約為5.4 r/min,并且當輪轂電機轉速大于約20 r/min時,各單輪行走系已不能穩定輸出正確的偏置軸轉角值。因此,取電機轉速范圍為[5.4, 20] r/min。左前單輪行走系電機轉速n分為5水平,具體取5.4、8、12、16和20 r/min。
3)底盤的切換角度β和β:在橫行姿態下,切換角度β僅為(90°-);在回轉姿態下,切換角度β的范圍為(0, 180°)。橫行姿態的切換角度β為(90°-)的單水平試驗;原地回轉姿態的切換角度β分為4水平,具體取45°、90°、135°和180°。
4)底盤的平移速度:當不考慮平移模式時,柔性底盤只有在橫行姿態的保持階段,才存在橫向平移。當柔性底盤工作在設施農業內部,從環境復雜度和使用安全的角度考慮,其運行速度應限定在[1, 4] m/s的范圍內。平移速度分為4水平,具體取1、2、3和4 m/s。
5)底盤的回轉速度:柔性底盤在原地回轉過程中,其回轉速度過大時,會造成底盤在制動過程中失穩,無法維持原地回轉的位置。通過試驗測定,回轉速度的穩定最低值約為0.349 rad/s,穩定最高值約為0.785 rad/s。因此,取回轉速度范圍為[0.35, 0.78] rad/s。回轉速度分為4水平,具體取0.35、0.50、0.65和0.78 rad/s。
上述各試驗因素依切換姿態的不同而在各姿態切換階段有所差異,具體如表1所示。
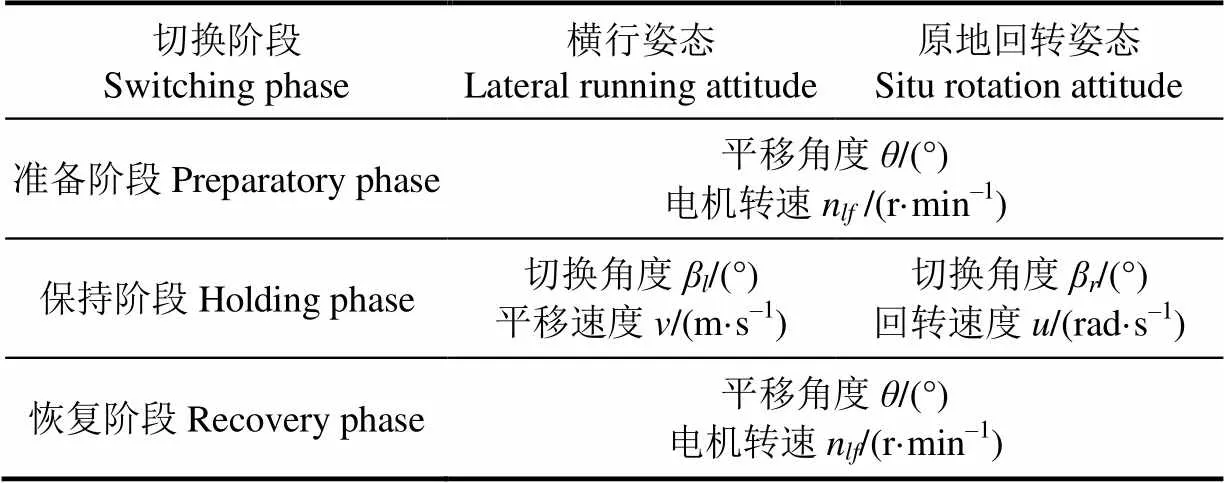
表1 柔性底盤姿態切換試驗因素
2.1.2 試驗指標
對柔性底盤各切換階段的考察,主要有2個方面:1)切換效率,即底盤完成此切換階段所花費的時間;2)切換精度,即在完成此切換階段后底盤的狀態是否穩定。
根據柔性底盤的切換階段,其所花費的時間對應分為準備時間、保持時間和恢復時間;而各階段完成后的精度對應分為準備精度、保持精度和恢復精度。特別的,在保持階段中,橫行姿態和原地回轉姿態因運動形式的不同而需要對其時間與精度指標進一步劃分。
上述各試驗指標依切換姿態的不同而在各切換階段有所差異,如表2所示。

表2 柔性底盤姿態切換試驗指標
由于柔性底盤在準備階段和恢復階段中,4個單輪行走系偏置軸轉角的配合關系一致,如前述式(2)所示。具體而言,當2個階段運轉完成后,4個單輪行走系偏置軸轉角的實測值越接近所要求的理論值時,即4個單輪行走系偏置軸轉角精度越高時,柔性底盤的運行狀態就越穩定。另外,柔性底盤在2個階段運轉完成后的狀態,是4個單輪行走系偏置軸轉角相互配合的結果。同時,4個單輪行走系的結構和功能相同,并采用對稱布置,對底盤運行狀態的影響效果是一致的。因此,柔性底盤在準備階段和恢復階段的準備精度和恢復精度,為4個單輪行走系偏置軸轉角精度的平均值,具體如式(3)所示。
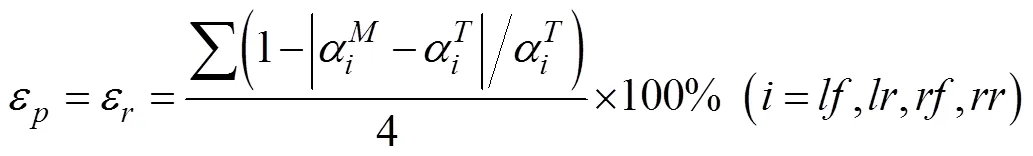
當采用橫行姿態時,柔性底盤在保持階段的運行狀態為橫向平移運動。當此階段運行完成后,橫向行駛的直線距離的實測值越接近設定的理論值,即橫行距離的精度越高,柔性底盤的運行狀態越穩定。橫行精度的具體計算如式(4)所示:
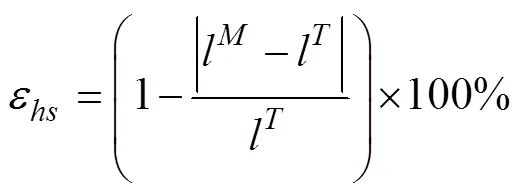
當采用原地回轉姿態時,柔性底盤在保持階段的運行狀態為原地回轉運動。當此階段運行完成后,原地回轉所轉過角度的實測值越接近設定的理論值,即原地回轉角度的精度越高,柔性底盤的運行狀態越穩定。回轉精度的具體計算如式(5)所示:
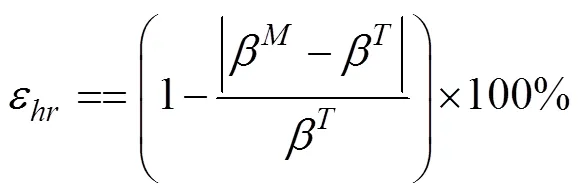
2.2 試驗準備與實施
選取柔性底盤二代樣機為測試對象進行試驗,選用平直的水泥路面作為測試場地。2種切換姿態下的分段試驗各重復5次。柔性底盤二代樣機以及運行模式如圖2所示。
各單輪行走系偏置軸轉角α的測量值采用上海盤卓自動化科技有限公司生產的P3022-V1-CW360型霍爾角度傳感器進行測量,其分辨率為0.01°,機械行程為0~360°。通過式(3)得到準備精度ε和恢復精度ε。
柔性底盤在橫行姿態保持階段的平移距離通過手工測量,采用上海美耐特實業有限公司生產的MNT135008型圓盤尺,其測量范圍為0~50 m,精度為1 mm。通過式(4)得到橫行姿態的橫行精度ε。

柔性底盤在原地回轉姿態保持階段的切換角度β采用深圳維特智能科技有限公司生產的WT-901型九軸陀螺儀姿態傳感器進行測量,其角度量程為±180°,分辨率為0.6(°)/s,動態精度為0.1°。通過式(5)得到回轉精度ε。
柔性底盤在各運行階段所持續的時間由意法半導體集團生產的STM32F103ZET6型MCU監測,采用內部16位的通用定時器進行數據采集,并輸出為準備時間t、橫行時間t、回轉時間t和恢復時間t。
3 試驗結果與分析
3.1 準備與恢復階段試驗結果與分析
圖3和表3分別為為柔性底盤2種切換姿態中準備階段和恢復階段的試驗結果和方差分析。精度指標測試結果表明,橫行姿態和原地回轉姿態的準備精度ε整體上都略高于恢復精度ε;并且橫行姿態的準備精度ε和恢復精度ε略高于原地回轉姿態。在橫行姿態中,準備精度ε的范圍為96.03%~99.53%,恢復精度ε的范圍為95.70%~99.31%;在原地回轉姿態中,準備精度ε的范圍為94.25%~99.06%,恢復精度ε的范圍為94.34%~98.87%。方差分析表明,2種切換姿態在準備(恢復)階段中,平移角度和電機轉速n對準備與恢復精度都有極顯著影響,對準備與恢復精度的影響程度一致,為平移角度<電機轉速n。原地回轉姿態下的平移角度對準備與恢復精度的影響程度大于橫行姿態,而電機轉速n的影響程度近似,二者間的交互作用在2種切換姿態下無影響。
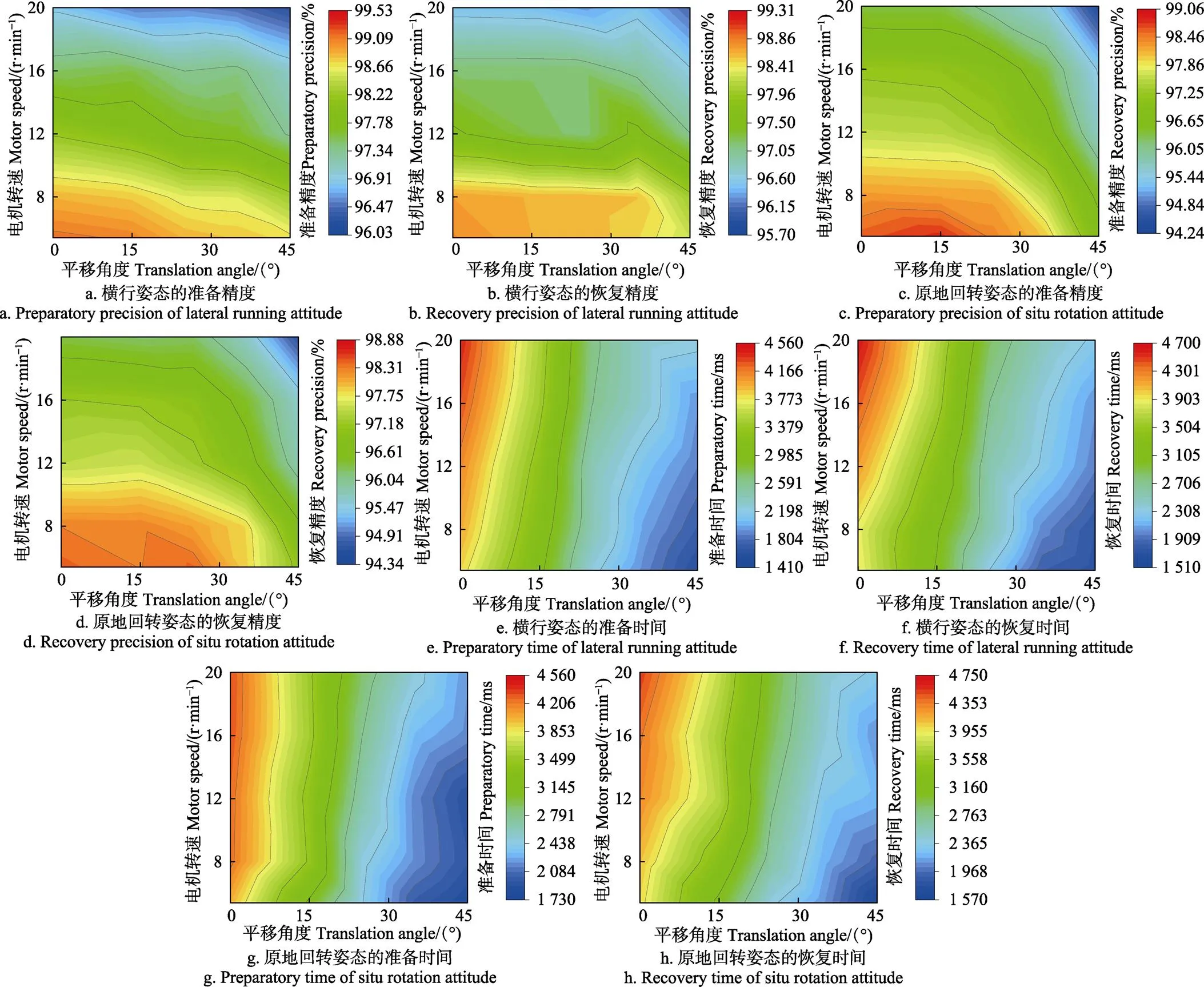
圖3 平移角度與電機轉速對準備(恢復)階段的影響
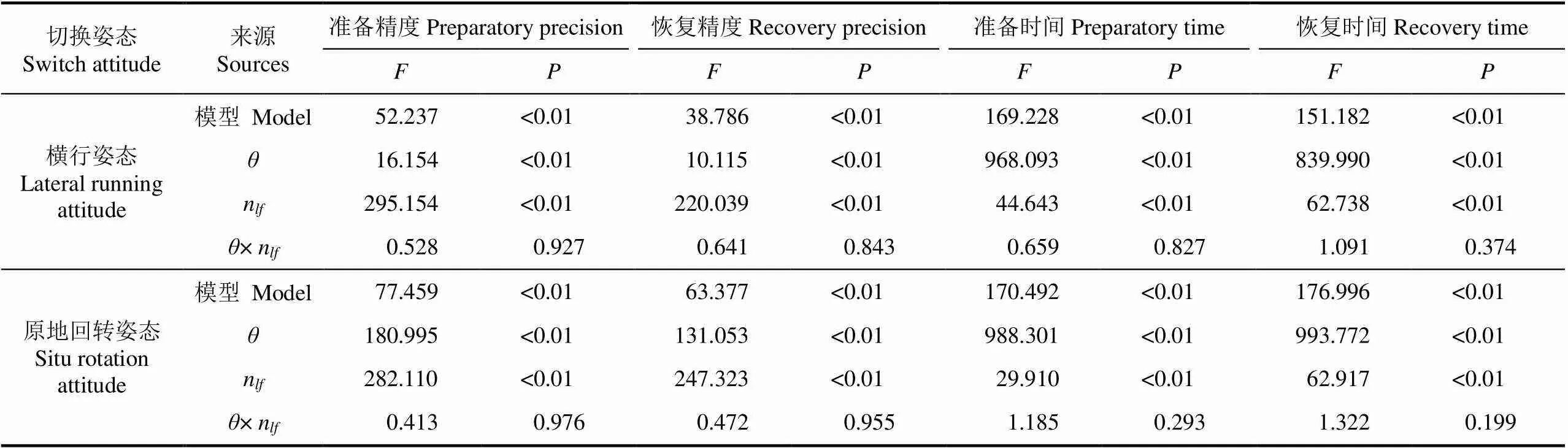
表3 準備(恢復)階段試驗結果方差分析
時間指標測試結果表明,2種切換姿態的準備時間t整體上略短于恢復時間t;橫行姿態的總體時間也略短于原地回轉姿態。在橫行姿態中,準備時間t的范圍為1 415~4 560 ms,恢復時間t的范圍為1 518~4 699 ms;在原地回轉姿態中,準備時間t的范圍為1 773~4 560 ms,恢復時間t的范圍為1 577~4 750 ms。方差分析表明,2種切換姿態程中,平移角度和電機轉速n對準備與恢復時間有極顯著的影響。其影響程度對于2種姿態的準備與恢復時間而言是一致的,為平移角度>電機轉速n。2種姿態中,各因素對準備與恢復時間的影響程度近似,而二者間的交互作用在2種切換姿態下無影響。
3.2 保持階段試驗結果與分析
圖4和表4分別為為柔性底盤橫行姿態中保持階段的試驗結果和方差分析。精度和時間指標測試結果表明,在橫行姿態的保持階段中,柔性底盤的橫行精度ε較為穩定,其范圍為93.86%~95.45%;而其橫行時間t隨平移速度變動劇烈,其范圍為14 686~31 811 ms。方差分析表明,平移速度對橫行精度ε和橫行時間t都有極顯著的影響。
圖5和表5分別為為柔性底盤原地回轉姿態中保持階段的試驗結果和方差分析。在原地回轉姿態的保持階段,其回轉精度ε的變動范圍較大,從90.68%~99.55%;并且回轉時間t的跨度較大,從2 091 ms到9 894 ms。方差分析表明,切換角度β和回轉速度對回轉精度ε有極顯著的影響,二者間的交互作用則無影響,其影響程度為切換角度β>回轉速度;切換角度β、回轉速度以及二者間的交互作用都對回轉時間t有極顯著的影響,其影響程度為切換角度β>回轉速度>交互作用。
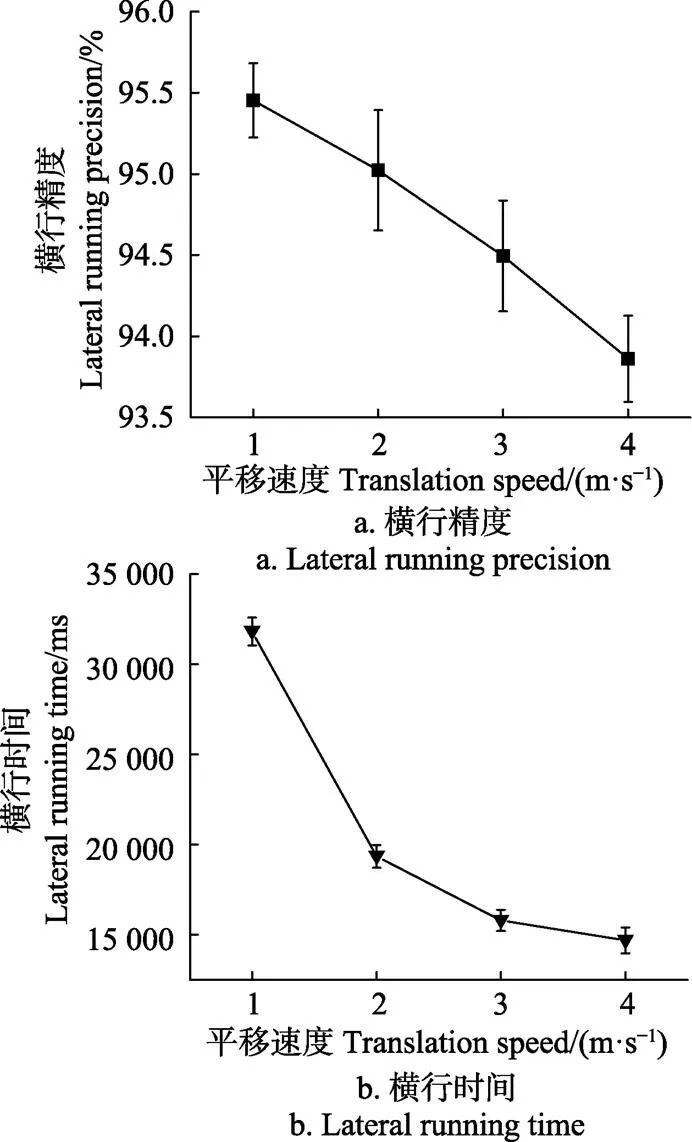
圖4 平移速度對橫行姿態保持階段的影響

表4 橫行姿態保持階段試驗結果方差分析

圖5 切換角度與回轉速度對原地回轉姿態保持階段的影響
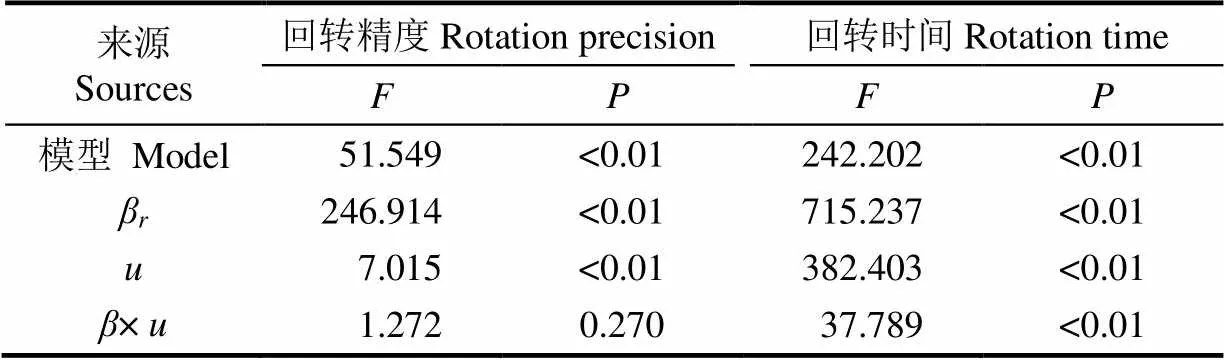
表5 原地回轉姿態保持階段試驗結果方差分析
3.3 姿態切換狀態模型
采用SPSS軟件對各試驗結果進行回歸分析,以求得2種切換姿態在整個切換過程中各指標的變化規律。依據切換姿態和3個切換階段將各回歸方程構建為2組柔性底盤姿態切換狀態模型。其中橫行姿態包括準備精度ε和時間t,橫行精度ε和時間t,以及恢復精度ε和時間t;而原地回轉姿態包括準備精度ε和時間t,回轉精度ε和時間t,以及恢復精度ε和時間t。各模型及其決定系數2具體表述如下:
橫行姿態:

回轉姿態:

4 姿態切換模式參數優化
為了保證柔性底盤在2種切換姿態下,運行過程的穩定可靠,需要根據上述姿態切換狀態模型進行最優解的求解與驗證。
4.1 指標權重確定
由于柔性底盤的切換過程為切換姿態和切換階段共同作用的結果,因此各試驗指標的相對重要性也各不相同[15-18]。所以在進行最優解求解前,需要對各試驗指標的權重值進行分析,具體采用層次分析法來確定[19-21]。
將3個切換階段定義為一級指標,各切換階段內被測量的試驗指標定義為二級指標,對上述指標以相對重要性進行兩兩對比,以1~9的標度對對比結果進行量化,構造各判斷矩陣。對判斷矩陣進行單排序計算來確定出各指標的權重,并對各判斷矩陣進行一致性檢驗來保證計算結果的科學性和可靠性[22-24]。
各級指標的權重確定遵循以下原則:1)2種姿態的各階段權重分布一致,即準備階段>保持階段>恢復階段;2)原地回轉姿態的保持階段相對于橫行姿態而言,其對整個換向過程的影響更大;3)在各階段內,各項精度指標的比重都要大于與之相對應的時間指標。各級指標的相對權重和二級指標權重值的計算結果如表6所示。
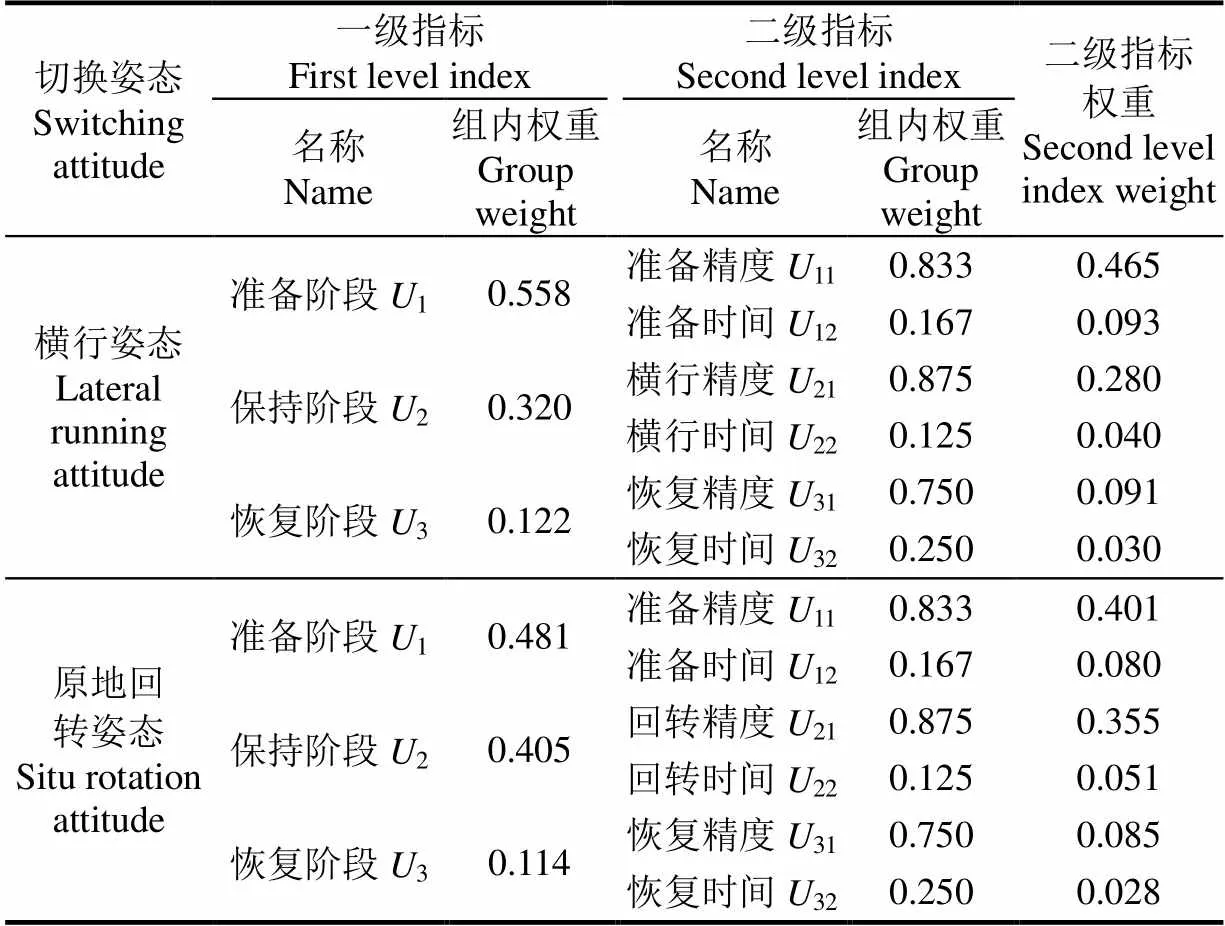
表6 姿態切換優化指標權重
4.2 參數優化
對于多元非線性方程組的計算,宜采用遺傳算法進行[25-28]。其中種群大小為300,迭代次數為200[29-30];遺傳操作為輪盤賭選擇法,單點交叉法,變異采用小概率變異[31-32]。
采用Matlab軟件進行編程并計算,2種切換姿態的參數優化結果如圖6所示。橫行姿態中,在任意平移角度下,電機轉速n和平移速度始終維持不變,前者處于最低值5.4 r/min,后者處于較高值3.45 m/s。原地回轉姿態中,在任意平移角度下,電機轉速n不隨切換角度β的增加而發生變化,始終維持在最低值5.4 r/min;而回轉速度隨切換角度β的增加而線性增加,表現為=(0.003 3β+0.506 8) rad/s(2=0.999),并且當切換角度β達到85°時,回轉速度達到最大值0.78 rad/s并持續穩定。

圖6 最優參數的變化趨勢
4.3 參數優化結果與驗證
4.3.1 優化結果驗證
在與前述試驗相同的條件下,對2種切換姿態的參數優化結果進行試驗驗證。對于橫行姿態,平移角度的水平分別為0、15°、30°和45°;對于原地回轉姿態,設定平移角度為45°,切換角度的水平分別為45°、90°、135°和180°。其余各參數按前述優化結果給定。
此時,需要考察的是柔性底盤完成整個姿態切換過程的結果,即試驗指標為綜合精度ε和綜合時間t。前者通過各階段運行精度的乘積表示,后者通過各階段運行時間之和來表示。各試驗重復5次,取綜合精度ε與綜合時間t的試驗值的平均數與理論值進行對比,并標明其標準差。試驗結果如圖7所示。
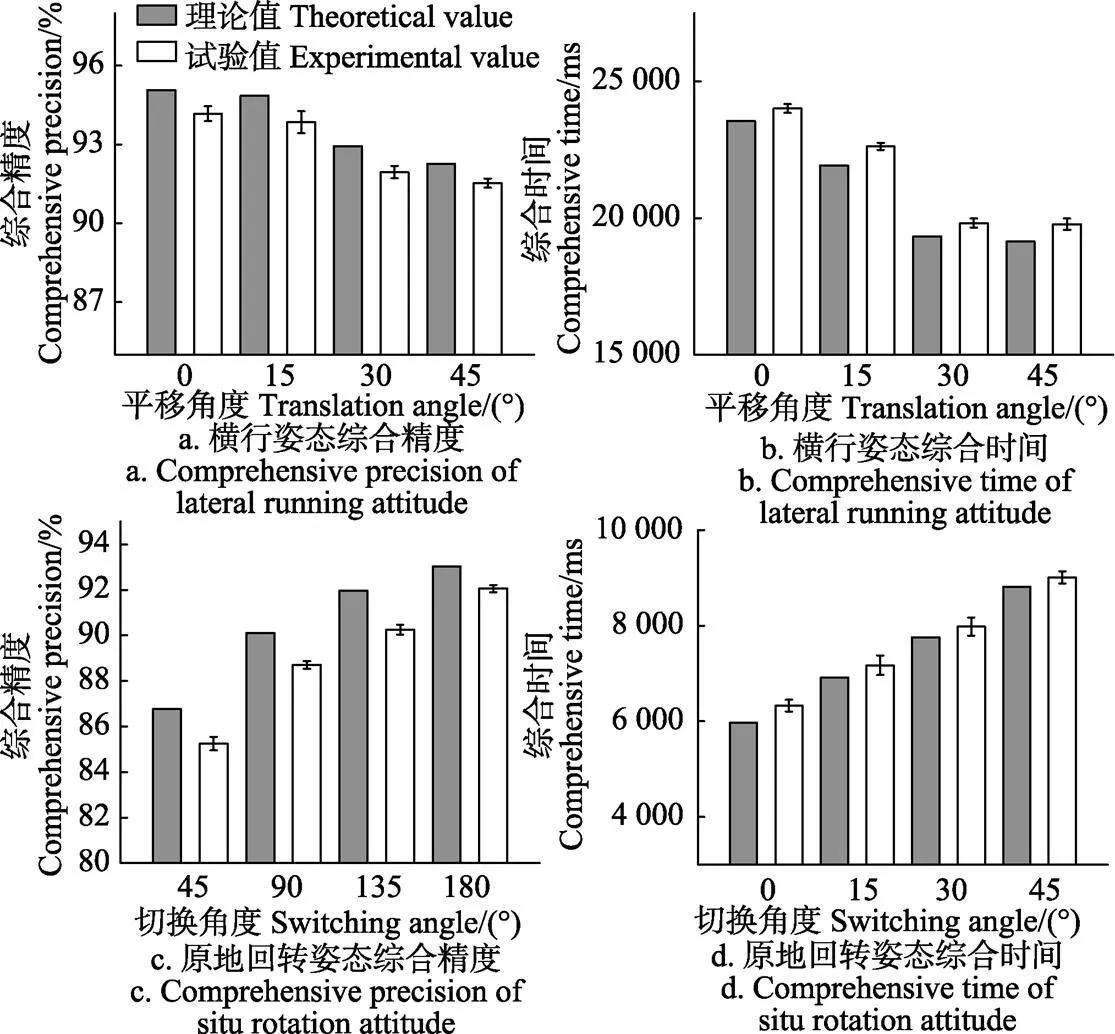
圖7 優化參數下的姿態切換結果驗證
從圖7中可以看出,2種切換姿態中綜合精度ε和綜合時間t的理論值和試驗值的總體趨勢都保持一致。對于綜合精度ε來說,試驗值略微偏低,在橫行姿態中其最大偏差為1.00%,最小偏差為0.75%;在原地回轉姿態中,其最大偏差為1.70%,最小偏差為0.97%。對于綜合時間t來說,試驗值總體偏高,在橫行姿態中其最大偏差為698 ms,最小偏差為454 ms;在原地回轉姿態中,其最大偏差為361 ms,最小偏差為191 ms。
驗證試驗中,試驗精度偏低與試驗時間偏高的原因在于,柔性底盤姿態切換狀態模型依據分步試驗建立,而驗證試驗為完整的姿態切換過程,受各階段相互作用導致的誤差累計更加明顯,但在可接受的范圍之內。
4.3.2 對比驗證
由前述試驗分析可知,在姿態切換模式的3個階段中,當柔性底盤以橫行姿態或原地回轉姿態運行時,相關試驗因素對底盤各精度和時間指標的影響總體上呈相反趨勢。具體而言,若沒有進行切換參數優化,則當底盤以最低速運行時,整個運行過程最為穩定,各項精度指標表現良好,但底盤姿態切換的效率大大降低;當底盤以最高速運行時,整個運行過程的穩定性變差,各項精度指標下降明顯,但底盤姿態切換的效率最高。因此,通過對比試驗來驗證各切換參數在優化前后對柔性底盤姿態切換過程的影響。
該驗證試驗的具體試驗條件與前述試驗相同。在橫行姿態中,平移角度取值為45°;在原地回轉姿態中,平移角度和切換角度β分別取值為25°和45°。
試驗分為3組:1)優化參數組;2)精度優先組;3)時間優先組。優化參數組中,電機轉速n、平移速度和回轉速度按前述優化內容給出,分別為5.4 r/min、3.45 m/s和0.66 rad/s。精度優先組中,電機轉速n、平移速度和回轉速度按最小值選定,分別為5.4 r/min、1 m/s和0.35 rad/s。時間優先組中,電機轉速n、平移速度和回轉速度按最大值選定,分別為20 r/min、4 m/s和0.78 rad/s。
以上各試驗重復5,取各精度和時間指標的平均值,并標注其標準差。試驗結果如圖8所示。
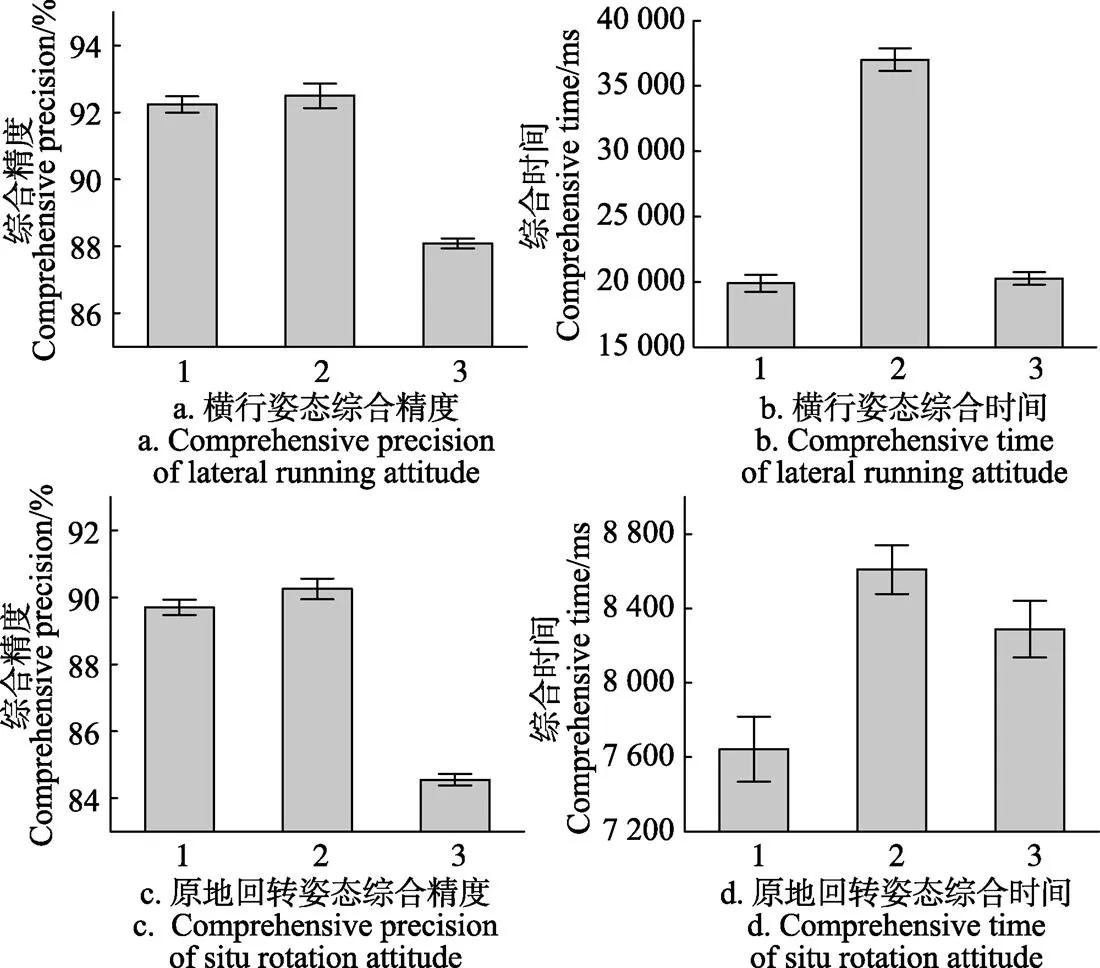
注:1、2、3分別表示優化參數組、精度優先組和時間優先組。
從圖8中可以看出,在橫行姿態下,優化參數組、精度優先組和時間優先組的綜合精度ε分別為92.24%、92.50%和88.08%,綜合時間t分別為19 893、37 003和20 256 ms。優化參數組的綜合精度與精度優先組持平并高出時間優先組4.16%,綜合時間與時間優先組持平并少于精度優先組17 110 ms。在原地回轉姿態下,優化參數組、精度優先組和時間優先組的綜合精度ε分別為89.70%、90.25%和84.55%,綜合時間t分別為7 643 ms、8 609 ms和8 289 ms。優化參數組的綜合精度與精度優先組持平并高出時間優先組5.15%,綜合時間少于時間優先組646 ms并少于精度優先組996 ms。
以上對比試驗結果說明,相對于未優化的姿態切換過程,采用層次分析法和遺傳算法對柔性底盤姿態切換參數進行優化后,能夠保證柔性底盤在略微損失運行精度的情況下,以較快的運行效率完成其姿態切換過程。
5 結 論
1)柔性底盤的橫行或原地回轉姿態通過準備、保持與恢復3個階段完成姿態切換過程。切換參數包括平移角度、電機轉速、切換角度、平移速度和回轉速度。底盤的準備與恢復階段中,平移角度和電機轉速對2種切換姿態的影響趨于一致,影響準備與恢復精度的主次因素為電機轉速>平移角度;影響準備與恢復時間的主次因素為平移角度>電機轉速。底盤的保持階段中,對于橫行姿態而言,平移速度對其橫行精度和時間都有極顯著影響。而對于原地回轉姿態,影響回轉精度的主次因素為切換角度>回轉速度;影響回轉時間的主次因素為切換角度>回轉速度>交互作用。
2)依據柔性底盤姿態切換各階段的試驗結果,得到由多元非線性方程組構建的柔性底盤姿態切換狀態模型。模型中各精度指標回歸方程的2∈[0.825, 0.936],各時間指標回歸方程的2∈[0.959, 0.981]。
3)采用層次分析法確定了各試驗指標的權重值,通過遺傳算法對柔性底盤姿態切換狀態模型的最優解進行了計算,并通過驗證試驗證明了模型的有效性。優化結果表明:橫行姿態中,任意平移角度下,最優電機轉速為5.4 r/min,最優平移速度為3.45 m/s。原地回轉姿態中,任意平移角度下,最優電機轉速為5.4 r/min;當切換角度β∈(0, 85)°時,最優回轉速度為(0.003 3β+0.506 8) rad/s,當切換角度β≥85°時,最優回轉速度為0.78 rad/s。
[1] 肖體瓊,何春霞,陳巧敏,等. 基于機械化生產視角的中國蔬菜成本收益分析[J]. 農業機械學報,2015,46(5):75-82. Xiao Tiqiong, He Chunxia, Chen Qiaomin, et al. Cost-benefit analysis of vegetable production based on agricultural mechanized production[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(5): 75-82. (in Chinese with English abstract)
[2] 齊飛,魏曉明,張躍峰. 中國設施園藝裝備技術發展現狀與未來研究方向[J]. 農業工程學報,2017,33(24):1-9. Qi Fei, Wei Xiaoming, Zhang Yuefeng. Development status and future research emphase on greenhouse horticultural equipment and its relative technology in China[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(24): 1-9. (in Chinese with English abstract)
[3] Trypanagnostopoulos G, Kavga A, Souliotis M, et al. Greenhouse performance results for roof installed photovoltaics[J]. Renewable Energy, 2017(111): 724-731.
[4] 張鐵民,黃翰,黃鵬煥. 電動輪式移動小車控制系統設計與試驗[J]. 農業工程學報,2014,30(19):11-18. Zhang Tiemin, Huang Han, Huang Penghuan. Design and test of drive and control system for electric wheeled mobile car[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(19): 11-18. (in Chinese with English abstract)
[5] 張鐵民,李輝輝,陳大為,等. 多源傳感器信息融合的農用小車路徑跟蹤導航系統[J]. 農業機械學報,2015,46(3):37-42. Zhang Tiemin, Li Huihui, Chen Dawei, et al. Agricultural vehicle path tracking navigation system based on information fusion of multi-source sensor[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3): 37-42. (in Chinese with English abstract)
[6] 張京,陳度,王書茂,等. 農用輪式機器人四輪獨立轉向驅動控制系統設計與試驗[J]. 農業工程學報,2015,31(18):63-70. Zhang Jing, Chen Du, Wang Shumao, et al. Design and experiment of four-wheel independent steering driving and control system for agricultural wheeled robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(18): 63-70. (in Chinese with English abstract)
[7] Ko M H, Ryuh B S, Kim K C, et al. Autonomous greenhouse mobile robot driving strategies from system integration perspective: Review and application[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(4): 1705-1716.
[8] Oksanen T and Linkolehto R. Control of four wheel steering using independent actuators[J]. 4th IFAC Conference on Modelling and Control in Agriculture, Horticulture and Post Harvest Industry. Finland: IFAC Secretariat, 2013, 46(18): 159-163.
[9] 宋樹杰,瞿濟偉,李翊寧,等. 農用車底盤偏置轉向軸驅動輪運動與動力特性試驗[J]. 農業工程學報,2015,31(23):28-34. Song Shujie, Qu Jiwei, Li Yining, et al. Experiment on movement and dynamic property of driving wheel with offset steering shaft for agricultural vehicle[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(23): 28-34. (in Chinese with English abstract)
[10] 宋樹杰,李翊寧,瞿濟偉,等. 柔性底盤性能檢測試驗臺設計與應用[J]. 農業機械學報,2016,47(2):77-83. Song Shujie, Li Yining, Qu Jiwei, et al. Development and application of test bench for flexible chassis[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(2): 77-83. (in Chinese with English abstract)
[11] Song S J, Li Y N, Qu J W, et al., Design and test of flexible chassis automatic tracking steering system[J]. International Journal of Agricultural and Biological Engineering, 2017, 10(5): 45-54.
[12] 瞿濟偉,郭康權,高華,等. 基于PWM信號的農用柔性底盤驅動與轉向協同控制特性試驗[J]. 農業工程學報,2018,34(7):75-81. Qu Jiwei, Guo Kangquan, Gao Hua, et al. Experiments on collaborative characteristics of driving and steering for agricultural flexible chassis based on PWM signal[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 75-81. (in Chinese with English abstract)
[13] 瞿濟偉,郭康權,李翊寧,等. 農用柔性底盤模式切換控制參數試驗與優化[J]. 農業機械學報,2018,49(9):346-352. Qu Jiwei, Guo Kangquan, Li Yining, et al. Experiment and optimization of mode switching controlling parameters for agricultural flexible chassis[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(9): 346-352. (in Chinese with English abstract)
[14] 李翊寧,周偉,宋樹杰,等. 溫室作業用柔性底盤試驗樣機的設計[J]. 農業工程學報,2017,33(19):41-50. Li Yining, Zhou Wei, Song Shujie, et al. Design of experimental prototype of flexible chassis used in greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 41-50. (in Chinese with English abstract)
[15] 向欣,羅煜,程紅勝,等. 基于層次分析法和模糊綜合評價的沼氣工程技術篩選[J]. 農業工程學報,2014,30(18):205-212. Xiang Xin, Luo Yu, Cheng Hongsheng, et al. Biogas engineering technology screening based on analytic hierarchy process and fuzzy comprehensive evaluation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(18): 205-212. (in Chinese with English abstract)
[16] Jote N, Beshah B, Kitaw D. Ethiopian livestock husbandry cluster identification using FUZZY-AHP approach[J]. Advances in Intelligent Systems and Computing, 2015(334): 233-243.
[17] Svoray T, Levi R, Zaidenberg R, et al. The effect of cultivation method on erosion in agricultural catchments: Integrating AHP in GIS environments[J]. Earth Surface Processes and Landforms, 2015, 40(6): 711-725.
[18] Huang W, Liu H J. Application of fuzzy dynamic weights drivability evaluation model in tip-in condition[J]. Journal of Vibration and Control, 2019, 25(4): 739-747.
[19] 龔艷,張曉,劉燕,等. 基于層次分析法的植保機械適用性綜合評價方法[J]. 農業機械學報,2016,47(9):73-78. Gong Yan, Zhang Xiao, Liu Yan, et al. Comprehensive evaluation method for applicability of plant protection machinery based on analytic hierarchy process[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(9): 73-78. (in Chinese with English abstract)
[20] Kumar A, Singh A R, Deng Y, et al. Integrated assessment of a sustainable microgrid for a remote village in hilly region[J]. Energy Conversion and Management, 2019(180): 442-472.
[21] 李風,付開進,于向軍. 基于層次分析法的大型半自磨機磨礦性能優化[J]. 農業機械學報,2017,48(6):392-398. Li Feng, Fu Kaijin, Yu Xiangjun. Optimization of grinding performance for large-type semi-autogenous mill based on analytic hierarchy process[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(6): 392-398. (in Chinese with English abstract)
[22] Zhang J Q, Su Y R, Wu J S, et al. GIS based land suitability assessment for tobacco production using AHP and fuzzy set in Shandong province of China[J]. Computers and Electronics in Agriculture, 2017, 48(6): 392-398.
[23] Veisi H, Liaghati H, Alipour A. Developing an ethics-based approach to indicators of sustainable agriculture using analytic hierarchy process (AHP)[J]. Ecological Indicators, 2016(60): 644-654.
[24] Kuo C F J, Liu J M, Umar M L, et al. The photovoltaic- thermal system parameter optimization design and practical verification[J]. Energy Conversion and Management, 2019(180): 358-371.
[25] 趙淑紅,劉宏俊,張先民,等. 滑推式開溝器設計與作業性能優化試驗[J]. 農業工程學報,2016,32(19):26-34. Zhao Shuhong, Liu Hongjun, Zhang Xianmin, et al. Design and optimization experiment of working performance of sliding push opener[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(19): 26-34. (in Chinese with English abstract)
[26] Caraballo S C, Rodriguez J L O, Ruiz J A L, et al. Optimization of a butterfly valve disc using 3D topology and genetic algorithms[J]. Structural and Multidisciplinary Optimization, 2017, 56(4): 941-957.
[27] Beirow B, Figaschewsky F, Kuhhorn A, et al. Vibration analysis of an axial turbine blisk with optimized intentional mistuning pattern[J]. Journal of Sound and Vibration, 2019(442): 11-27.
[28] 高若婉,李麗,梅樹立,等. 基于遺傳算法的苦瓜片真空冷凍干燥工藝優化[J]. 農業機械學報,2017,48(增刊):401-406. Gao Ruowan, Li Li, Mei Shuli, et al. Optimization of vacuum freeze-drying process of bitter melon slices using genetic algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(S1): 401-406. (in Chinese with English abstract)
[29] 張忠學,張世偉,郭丹丹,等. 玉米不同水肥條件的耦合效應分析與水肥配施方案尋優[J]. 農業機械學報,2017,48(9):206-214. Zhang Zhongxue, Zhang Shiwei, Guo Dandan, et al. Coupling effects of different water and fertilizer conditions and optimization of water and fertilizer schemes on maize[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(9): 206-214. (in Chinese with English abstract)
[30] Rosyid A, El-Khasawneh B, Alazzam A. Genetic and hybrid algorithms for optimization of non-singular 3PRR planar parallel kinematics mechanism for machining application[J]. Robotica, 2018, 36(6): 839-864.
[31] Khosravi H, Salehi G R, Azad M T. Design of structure and optimization of organic Rankine cycle for heat recovery from gas turbine: The use of 4E, advanced exergy and advanced exergoeconomic analysis[J]. Applied Thermal Engineering, 2019(147): 272-290.
[32] Saadabad N A, Moradi H, Vossoughi G. Dynamic modeling, optimized design, and fabrication of a 2DOF piezo-actuated stick-slip mobile microrobot[J]. Mechanism and Machine Theory, 2019(133): 514-530.
Effects of attitude switching parameters on switching precision and time of flexible chassis of agricultural vehicles and its optimization
Li Yining1, Guo Kangquan1,2※, Tran Van Cuong3, Qu Jiwei1, Gao Hua1
(1.712100,;2.712100,;3.1,15910,)
In order to study the attitude switching operation characteristics of the flexible chassis of agricultural vehicles, the attitude switching analysis of the flexible chassis and the attitude switching test based on the second-generation prototype running on the hard surface were carried out. The attitude switching state model was established, and the switching parameters were optimized by the analytic hierarchy process and genetic algorithm. The index weights were determined for the lateral running attitude and the situ rotation attitude, respectively. The first level indicator included the preparatory phase, the holding phase and the recovery phase in the attitude switching process. The secondary indicators included all test indicators such as preparatory precision, preparatory time, lateral precision, lateral time, rotation precision, rotation time, recovery precision and recovery time. The population size of genetic algorithm was 300 and the number of iterations was 200, the genetic operation was roulette selection method and single point intersection method, and the variation used the small probability variation. Through the study of the switching precision and switching time under different translation angle, motor speed, switching angle, translation speed and rotating speed were obtained, the influence of various factors and their interactions on the attitude switching of the flexible chassis and the matching relationship between different switching attitude parameters were obtained. The results showed that the primary and secondary factors affecting the preparatory and recovery precision were the translation angle
agricultural machinery; vehicles; flexible chassis; attitude switching; parameter optimization; analytic hierarchy process; genetic algorithm
2018-11-19
2019-01-24
國家自然科學基金項目(51375401)
李翊寧,博士生,主要從事智能化農業裝備與技術的研究。Email:liyining_work@163.com
郭康權,教授,博士生導師,主要從事農業技術裝備的研究。Email:jdgkq@nusuaf.edu.cn
10.11975/j.issn.1002-6819.2019.05.007
S229+.1;U463.1
A
1002-6819(2019)-05-0051-11
李翊寧,郭康權,陳文強,瞿濟偉,高 華. 農用車柔性底盤姿態切換參數對切換精度與時間的影響及其優化[J]. 農業工程學報,2019,35(5):51-61. doi:10.11975/j.issn.1002-6819.2019.05.007 http://www.tcsae.org
Li Yining, Guo Kangquan,Tran Van Cuong, Qu Jiwei, Gao Hua. Effects of attitude switching parameters on switching precision and time of flexible chassis of agricultural vehicles and its optimization[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(5): 51-61. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2019.05.007 http://www.tcsae.org

