運載火箭結構振動疲勞損傷的工程分析方法
薛立鵬,李文斌,司群英,葉 超,孫善秀
(北京宇航系統工程研究所,北京,100076)
0 引言
運載火箭結構在飛行過程中要承受復雜的振動載荷,在研制過程中要進行正弦振動、定頻振動及隨機振動力學環境考核試驗[1,2],當振動量級較大,結構疲勞強度不足時容易發生疲勞破壞,在新型運載火箭研制的過程中曾發生過結構振動疲勞破壞的現象,振動疲勞的本質是結構所受動態交變載荷(如振動、沖擊、噪聲載荷等)的頻率分布與結構固有頻率分布具有交集或相接近,從而使結構產生共振所導致的疲勞破壞現象[3],對于復雜結構的振動疲勞分析,通常采用有限元方法求得結構的應力響應,然后結合疲勞模型進行結構疲勞損傷的計算和評估。目前對于結構隨機振動疲勞損傷的計算研究較多[4~6],對于結構正弦振動和定頻振動研究較少[7]。本文根據Miner線性累計損傷理論結合相應的損傷模型推導了結構的正弦振動、定頻振動、隨機振動的疲勞損傷計算公式,并結合有限元方法,給出了運載火箭結構在正弦、定頻、隨機振動載荷下的疲勞損傷仿真分析方法和分析流程。
1 基于Miner線性累積損傷理論的結構振動疲勞損傷計算方法
Miner線性累積損傷理論[8]將疲勞損傷LD定義為使用應力下的循環次數n與該應力下材料疲勞壽命N的比,即:

在多級不同應力幅值作用下,疲勞損傷為

式中in為第i級應力水平下的循環次數;iN為第i級應力水平下的疲勞壽命,損傷小于1時結構不會發生疲勞破壞。
正弦振動過程中振動時間、頻率和掃描率的關系為
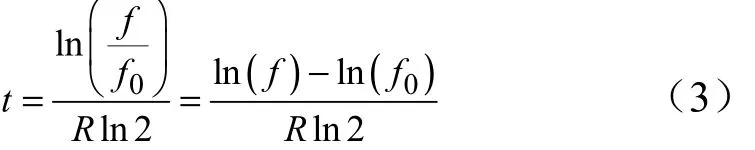
則,
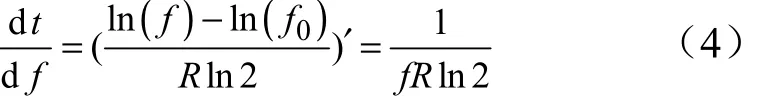
由以上各式得到的正弦振動時結構的疲勞損傷為
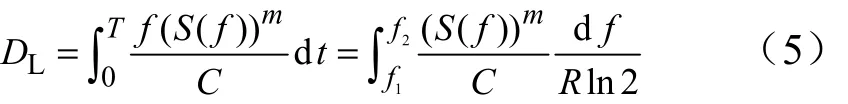
在振動過程中定頻振動應力發生的次數為

式中S為每秒內的應力;C為疲勞常數;R為掃描率;f為定頻振動頻率;T為振動狀態的持續時間。定頻振動時振動應力為一定值,則定頻振動時結構的損傷為
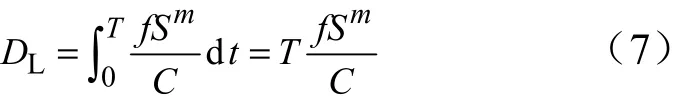
隨機振動基于Miner線性累計損傷模型和Dirlik方法,采用3個統計參數從隨機振動信號中估計振動應力水平及應力的周期數量[9],這3個參數分別為均值E( 0)、峰值E(p)和不規則因子γ,定義結構響應的n階慣性矩為
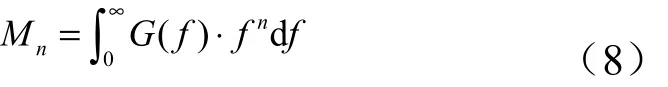
式中 ()G f為應力譜密度。
則,
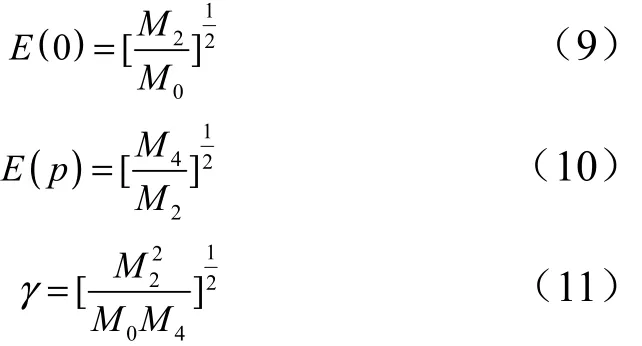
每秒內應力S對應的次數為

根據Dirlik公式有:
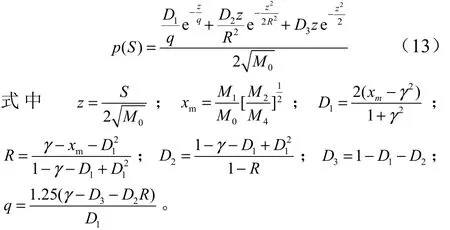
得到隨機振動時結構的疲勞損傷為
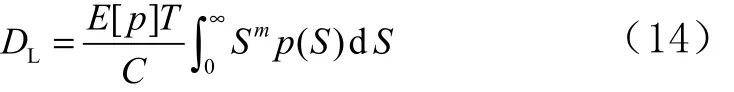
2 基于有限元方法的結構振動響應及疲勞損傷計算
2.1 基于有限元方法的結構振動疲勞損傷分析流程
基于有限元方法的結構振動疲勞損傷分析首先要進行振動載荷作用下結構的動力學響應分析,然后基于動力學響應分析結果進行結構的振動疲勞損傷估算,基于有限元方法的結構振動疲勞損傷一般采用頻域分析方法,結構振動疲勞損傷分析流程如圖1所示。
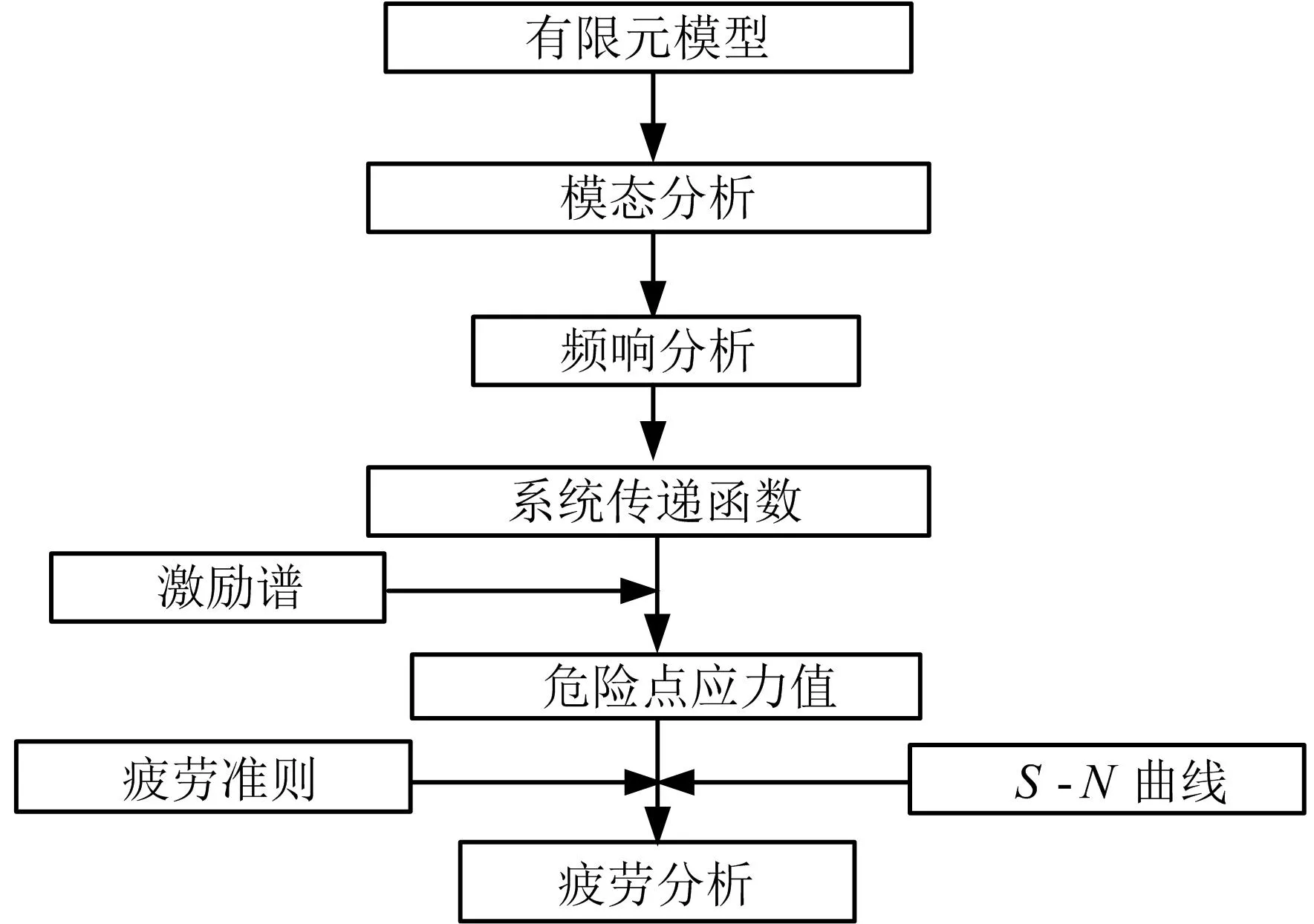
圖1 基于有限元方法的結構振動疲勞損傷分析流程示意Fig.1 Structural Vibration Fatigue Damage Analysis Process Based on Finite Element Method
2.2 基于有限元方法的結構應力響應分析
本文以管路為例,采用有限元方法計算結構的振動應力響應,管路材料為1Cr18Ni9Ti,管路正弦振動載荷條件如表1所示,定頻振動條件如表2所示,隨機振動條件如表3所示,振動均為3個方向,管路有限元分析模型如圖2所示。
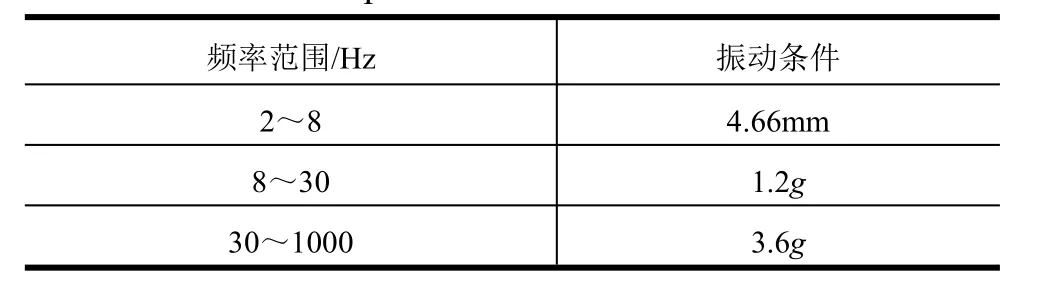
表1 結構正弦振動條件Tab.1 Sinsweep Vibration Conditions of Structures

表2 結構定頻振動試驗條件Tab.2 Dwell Vibration Conditions of Structures

表3 隨機振動條件Tab.3 Random Vibration Conditions

圖2 管路有限元分析模型示意Fig.2 Finite Element Analysis Model of Pipeline
管路兩端固定,內壓1.5 MPa,并在一端施加振動激勵,管路結構振動應力響應基于模態動力學分析方法,在求得結構頻響函數的基礎上,進而求得結構在振動條件下的應力等響應。管路結構部分模態的共振頻率和振型分析結果如圖3所示。
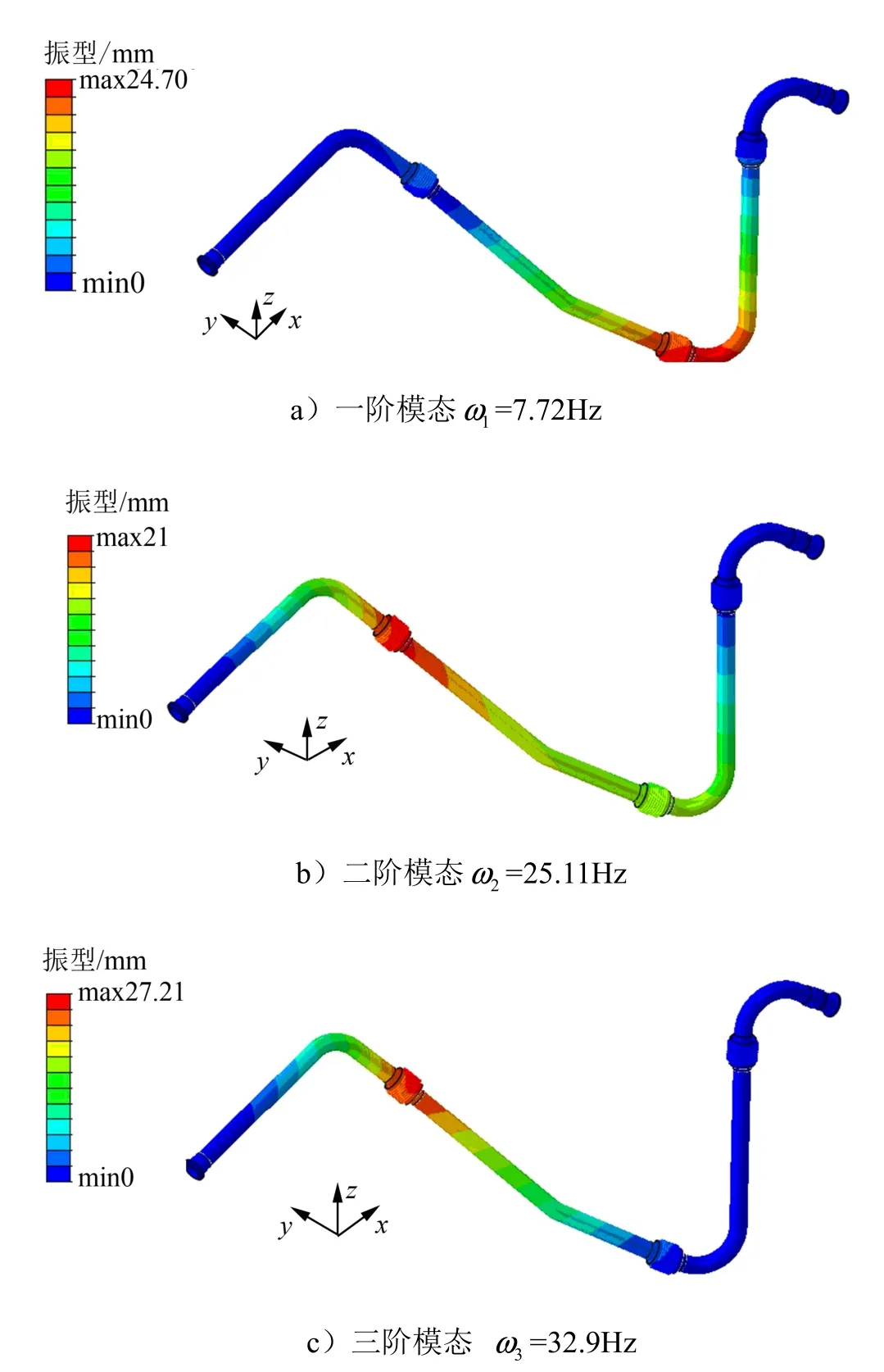
圖3 管路模態分析結果Fig.3 Modal Analysis of Pipeline
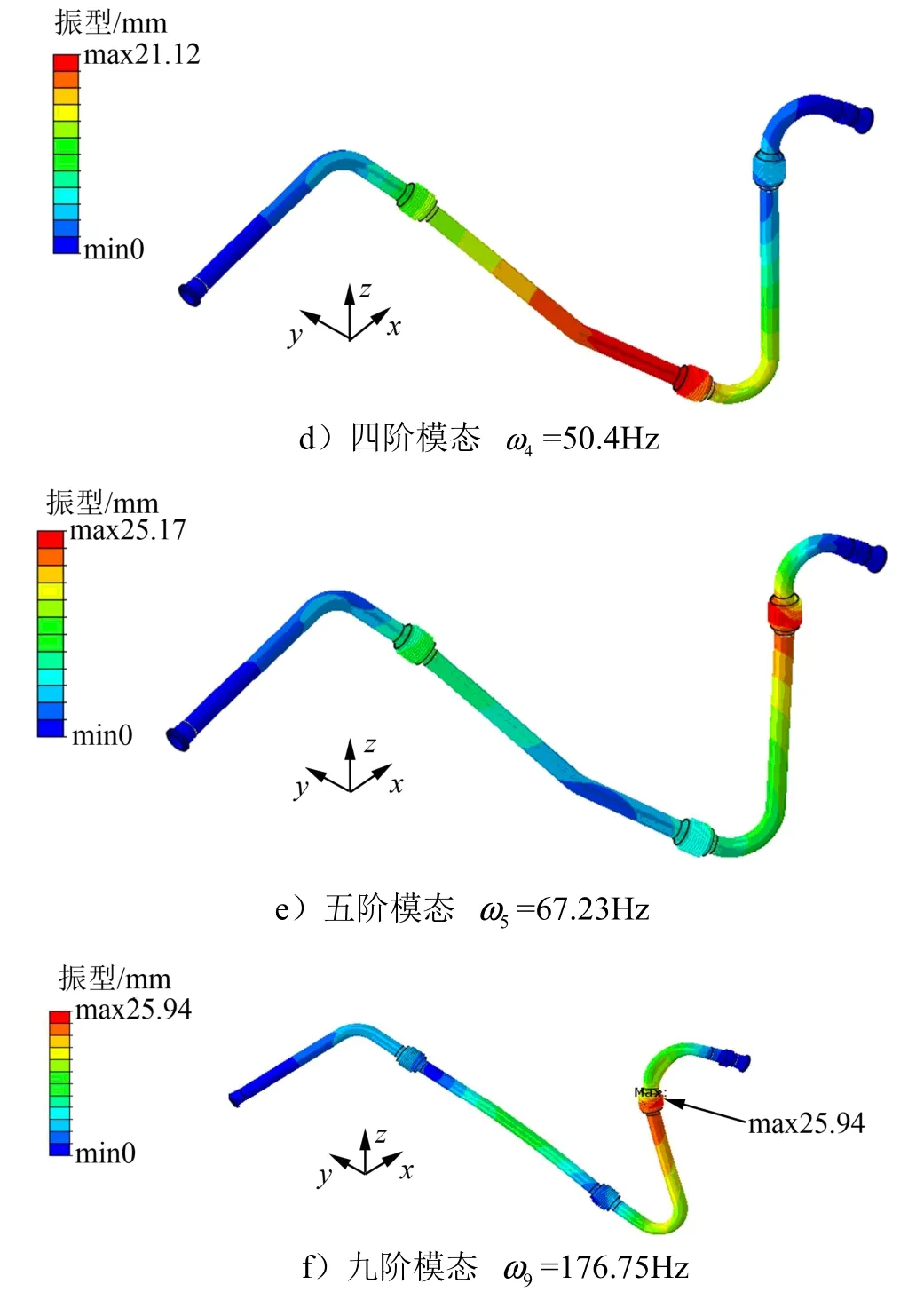
續圖3
正弦振動條件下管路應力響應云圖及結構應力最大點的應力響應如圖4所示。
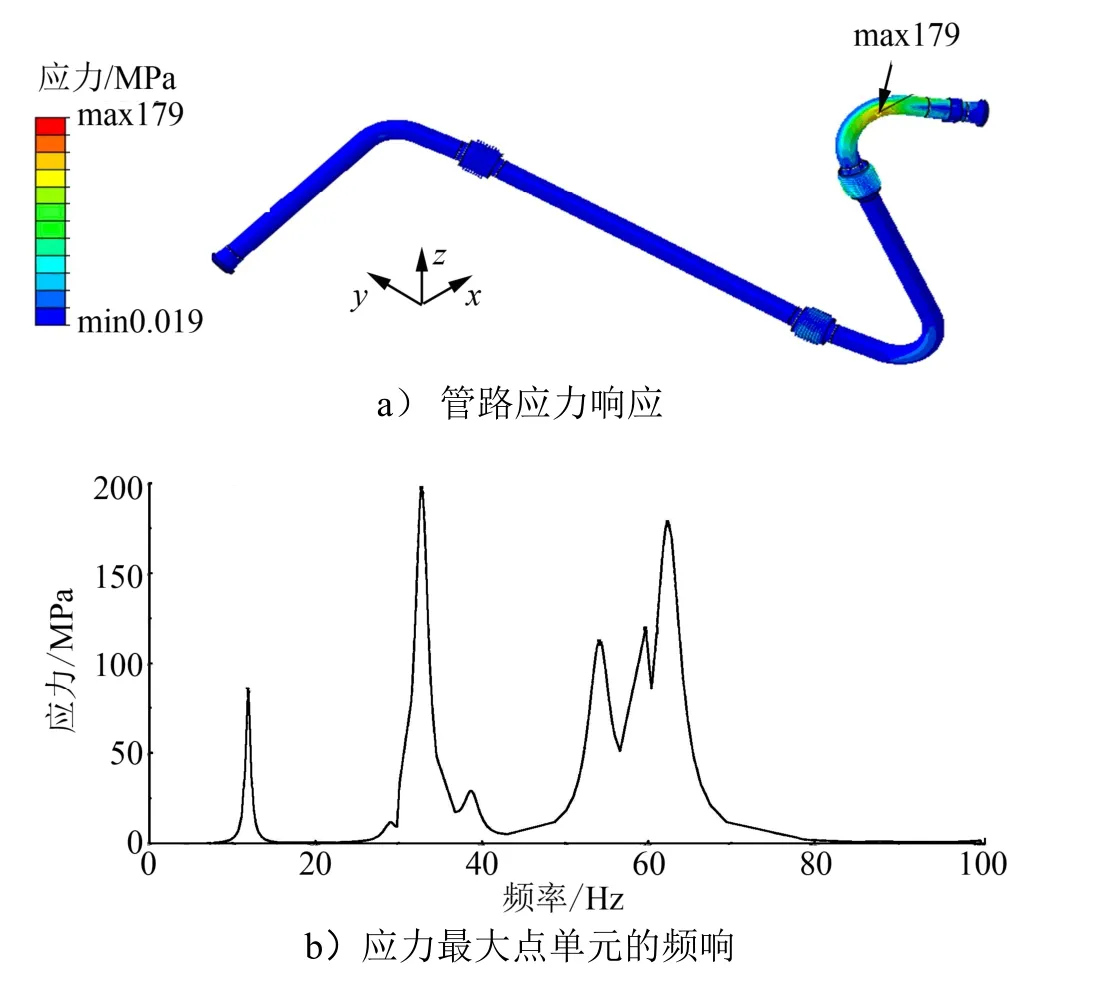
圖4 正弦振動管路應力云圖及應力最大點單元的頻響曲線Fig.4 Stress Cloud Chart and Frequency Response Curve of Sinsweep Vibration Pipeline
由圖4可知,管路上最大應力為179 MPa,對應管路的第3階模態。
定頻振動條件下管路應力響應如圖5所示。由圖5可知,管路上的最大應力為14.9 MPa。
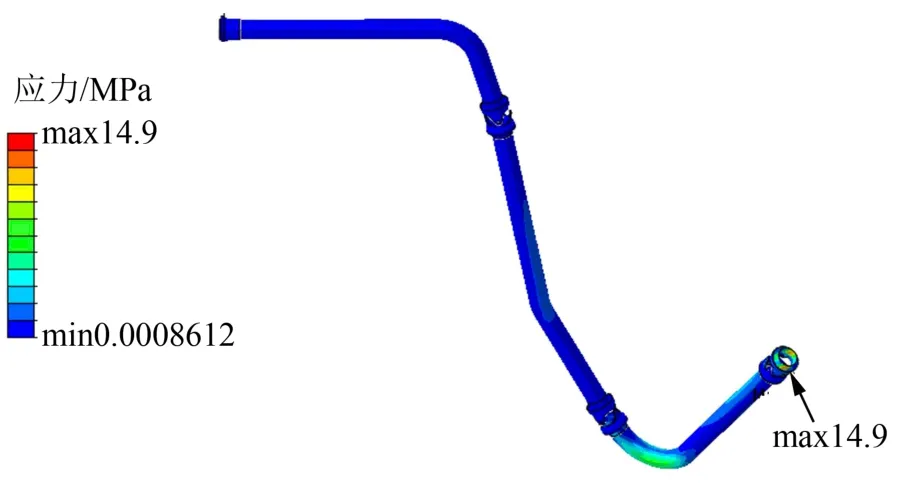
圖5 定頻振動管路應力云圖Fig.5 Stress Cloud Chart of Dwell Vibration Pipeline
隨機振動條件下管路應力響應及危險點應力譜密度如圖6所示。由圖6可知,管路上的最大均方根應力為40.25 MPa,主要是第5階和第9階共振頻率的激勵。
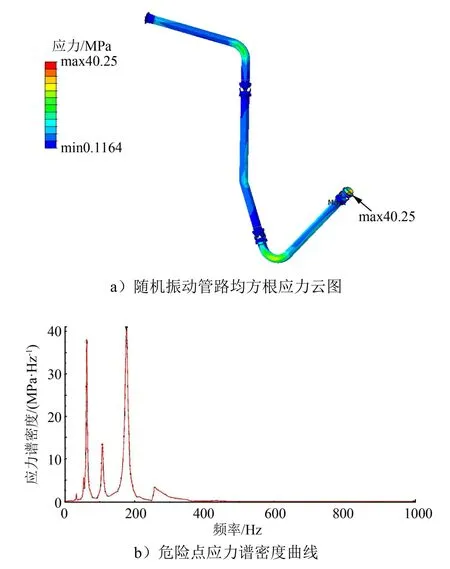
圖6 隨機振動管路均方根應力云圖及危險點應力譜密度曲線Fig.6 RMS Stress Cloud Chart of Random Vibration and Stress Spectrum Density Curve of Dangerous Point
2.3 振動疲勞損傷評估
采用Miner線性累積損傷理論計算結構的疲勞損傷,當損傷LD小于1時,結構一般不會發生疲勞破壞,當損傷LD不小于1時,結構發生疲勞破壞的可能性極高;采用Goodman方法考慮預應力的影響,管路在正弦、定頻和隨機振動載荷條件下的疲勞損傷計算和試驗結果如表4所示。由表4可知,計算結果和試驗結果一致,結構在給定的振動載荷下不會發生疲勞破壞。
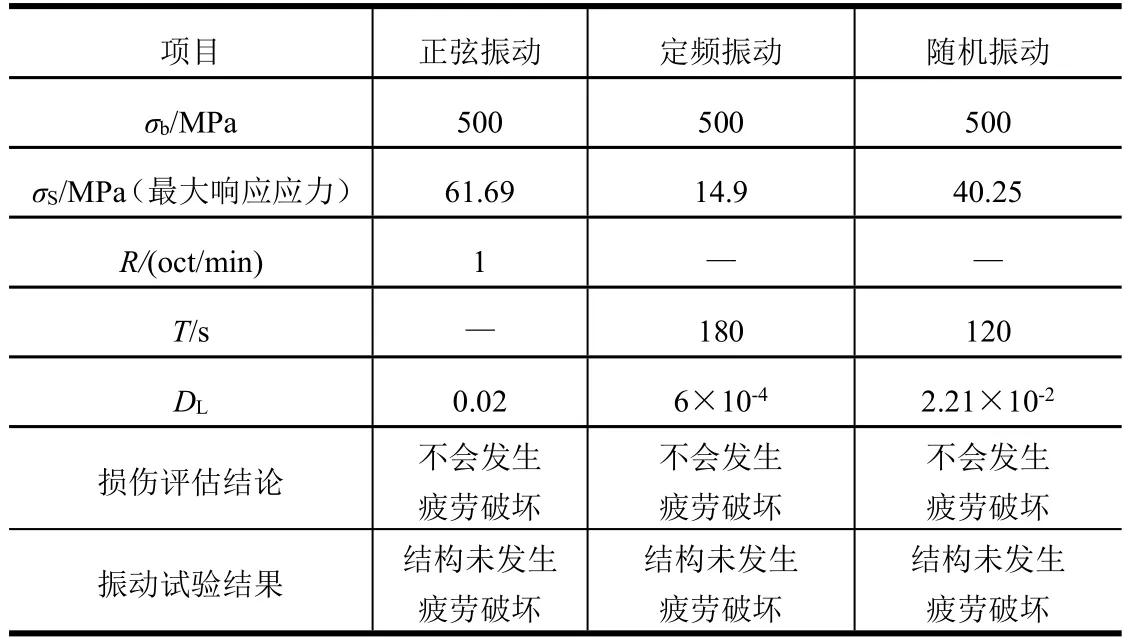
表4 管路正弦、定頻、隨機振動疲勞損傷預測及試驗Tab.4 Fatigue Damage Prediction and Test of Pipeline under Sinsweep,Fixed Frequency and Random Vibration
3 結論
a)本文基于Miner線性累計損傷理論推導了結構的正弦振動、定頻振動和隨機振動疲勞損傷計算公式,以管路為例,采用有限元軟件,基于模態的動力學分析方法計算了管路結構在正弦、定頻、隨機振動載荷下的振動響應及疲勞損傷并進行評估,結構不會發生疲勞破壞,與試驗結果吻合;
b)本文提出的計算方法和流程可用于指導運載火箭研制工程中結構的振動疲勞損傷分析,具有良好的工程應用價值。

