基于非線性維納過程的末制導炮彈控制艙光耦貯存壽命評定

張烜工，穆希輝

(1.陸軍工程大學石家莊校區 彈藥工程系， 石家莊 050003； 2.陸軍研究院特種勤務研究所， 石家莊 050003)

為了準確評定末制導炮彈控制艙光電耦合器的貯存壽命，選用了10枚樣品，對其進行了四應力步進加速退化試驗。以光耦的漏電流參數為刻畫對象，對其進行加速退化建模，進而評估其長儲可靠性。現階段來看，主流的性能退化建模有三種方法：性能退化軌道方法、退化量分布方法以及隨機過程方法[1]。前兩種方法較為簡單，應用最為廣泛且技術成熟。然而這兩者的缺陷在于忽略了樣品在退化過程中具有的隨機性。相比退化軌道方法或者退化量分布方法，基于隨機過程的方法考慮到退化過程具有的隨機性和動態性特征，能夠更好地反映環境等因素對產品性能的綜合影響，能更好地描述產品的真實退化過程。目前常用來構建退化模型的隨機過程主要有三個：維納過程、伽馬過程以及復合泊松過程[2]。維納過程和伽馬過程的主要區別在于前者可以描述退化增量可能出現負數的情況，而伽馬過程要求退化增量非負。復合泊松過程一般用來離散退化過程建模。三者中，維納過程應用最為廣泛。考慮到光耦的試驗數據退化增量有可能為負的情況，因此確定使用維納過程對光耦的漏電流退化數據進行建模。

1 基于隨機變量的加速模型的構建

1.1 漏電流維納過程建模面臨的重點

假設光耦漏電流的退化過程可以用維納過程進行描述：

X(t)=x0+λt+σWW(t)

(1)

式(1)中，x0是漏電流的初值；λ是漂移參數，表征退化速度；σW是擴散參數；W(t)是標準維納過程。

漏電流隨時間變化的散點連線如圖1所示。維納過程在應用過程中使用廣泛，但是面對漏電流的數據進行建模時，需要對以下兩個重點問題進行研究：(1)如何描述不同光耦漏電流退化的個體性差異；(2)漏電流非線性數據的處理。

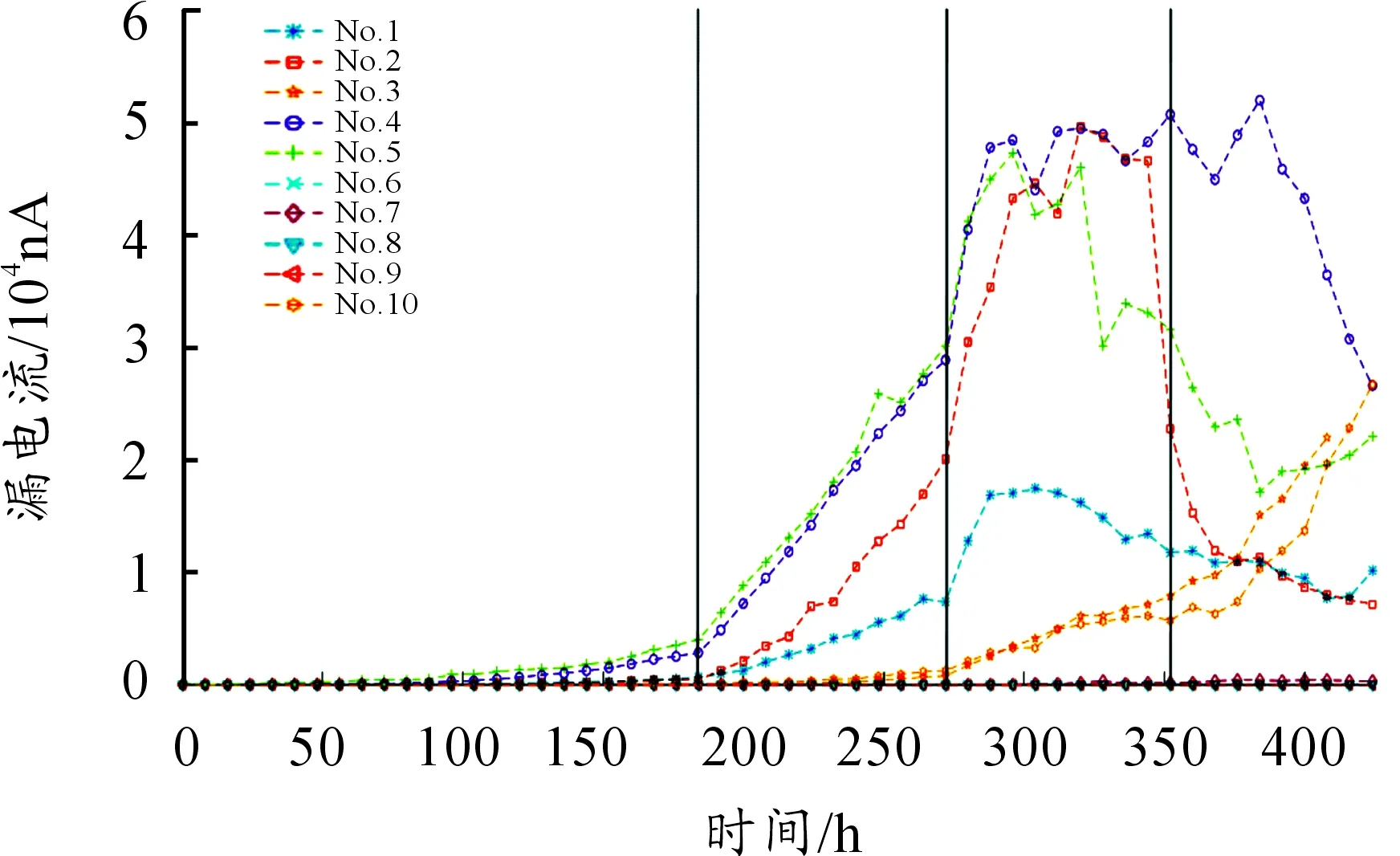
圖1 漏電流隨時間變化的散點連線

同一批光耦，由于在制造工藝、設計誤差以及環境、材料等因素的影響，表現出漏電流的退化速率不一致的個體性差異。在正式試驗過程中，由圖1可以看出，這種現象尤為突出。厲海濤[3]在對衛星動量輪進行可靠性評估時，將x0和λ均看作隨機變量，進而對動量輪進行可靠性評估。但是動量輪的數據是在非加速試驗條件下搜集的，亦即為實時監測數據，并不涉及加速問題。Wang[4]和郭波[5]將λ及σW都看成隨機變量，但是所假定的分布類型并未得到檢驗，而且其給出的EM算法計算復雜，并不適合推廣。蔡忠義[6]和唐圣金[7]將λ看成服從正態分布的隨機變量，給出了考慮個體差異的壽命模型，既便于計算又達到較好的模型擬合效果。目前關于非線性數據的處理主要是采用時間尺度變換模型，時間尺度變換模型最早由Whitmore[8]提出，諸多文獻采用其模型，實例證明其具有不錯的實用性[9]。

基于以上的分析，將漏電流退化數據進行時間尺度變換，使漏電流的非線性數據變為線性數據，然后將λ進行隨機化處理，構建考慮個體差異的加速退化模型，再采用兩步極大似然估計方法對未知參數進行估計。由于x0與失效閾值相比幾乎可以忽略不計，并且x0較為集中，僅有一個點游離于集中區域之外，因此將x0取均值，而不是把x0看成隨機變量，如果將其看成隨機變量，不僅沒有必要而且還會大大增加參數估計的復雜程度[10]。

1.2 基于隨機變量的加速模型

光耦漏電流的加速方程滿足阿倫尼烏斯加速模型，對于基于Wiener過程的退化模型而言，假定漂移系數λ與應力相關，則相應的加速模型為：

λi=aexp(-b/Ti)

(2)

式(2)中，a、b為未知常數；Ti為絕對溫度。

根據式(2)可以知道，在同一應力水平下，各個樣本的退化速度是一樣的。前文已述，個體性差異決定了不同光耦漏電流退化速率的不一致，誤差會隨著確定性參數的使用而產生。因此，提出一種基于隨機變量的阿倫尼烏斯模型，用以描述光耦之間的退化差異。則在第i個應力下第j個光耦的加速方程為：

(3)

通過式(3)可知，第i個應力下考慮光耦個體退化差異的漂移系數λi可以表示為：

(4)

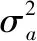
2 步進應力條件下基于維納過程的數據描述與非線性退化數據的建模

2.1 步進應力加速退化試驗數據統計模型

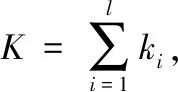
在第i個應力下，第j個光耦在第q次測量時相比第q-1次測量時性能退化增量為：

(6)

時間間隔為：

(7)

則根據維納過程的性質可得：

(8)

2.2 非線性退化數據的建模

對于非線性的數據，采用由Whitmore[8]提出的時間尺度變換模型，將其變為線性數據。其常見函數為：

τ=Λ(t)=tc

(9)

式(9)中，c為常數且大于0。當c<1時，數據為凸型退化，當c>1時，數據為凹型退化。這兩種數據均為非線性數據，而當c=1時，數據為線型退化，即線性數據。當數據中出現越來越多的非線性數據，c值開始慢慢偏離1，非線性數據越多，c值的偏離程度就越大。式(9)的優點在于可以處理線性與非線性數據并存的情況。

因此，本文采用上述變換模型，將漏電流數據[t,X(t)]改寫為[τ,Y(τ)]，故可以將式(1)改寫為：

Y(τ)=x0+λτ+σWW(τ)

(10)

設失效閾值為Df，則基于維納過程的光耦漏電流首達失效時的壽命可靠度函數為：

(11)

式(11)中，Φ(·)為標準正態分布函數。經過簡單推導，可以得到變換后的可靠度函數為：

(12)

令τ=Λ(t)，Y(τ)=X(t)，則式(12)可化為：

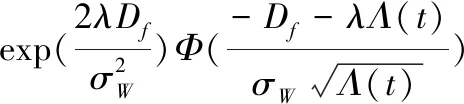
(13)

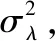
(14)

式(14)是最為關心的可靠度函數，由于λ與應力有關，因此嚴格來說這是一個二元函數，當應力給定時，如常應力，故又變成了一元函數[11]。因此下一步的重點就是估計式(14)中的相關參數。

3 可靠度函數的求解

3.1 兩步極大似然估計法

前文將漏電流數據[t,X(t)]變換為[τ,Y(τ)]，故式(8)可變換為：

(15)

式(15)中，

(16)

(17)

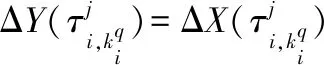
(18)

(19)

可以求出：

(20)

(21)

理論上來說，式(20)和式(21)在擁有退化數據情況下解出來的，但是仔細觀察上述兩式，都包含b和c，因此使用兩步估計法求解相關參數。

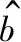
(22)

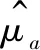
3.2 閾值與可靠度曲線

通過前面的推導和建立的模型，給定n=6，l=4，k1=23，k2=11，k3=10，k4=9，T1=70+273.15，T2=90+273.15，T3=110+273.15，T0=25+273.15，結合測量的數據，可以計算出維納過程漂移系數、擴散系數等各項參數值如表1所示。

表1 各項參數估計值

現在所關心的是失效閾值Df。根據摸底情況來看，當Df=70 μA時，光耦進入不穩定狀態，但是那時光耦已經產生了實質性失效，即不能完成預定功能。通過與光耦生產廠家進行溝通，廠家也給不出明確的說法，因為沒有對該產品貯存可靠性進行深入研究，因此也無法提供具體的失效閾值。因此，經過討論，決定設立游動閾值，即從60 μA開始，2 μA為步長，一直到70 μA。其可靠度曲線如圖2所示。

圖2 基于游動閾值的光耦維納過程可靠度曲線

如圖2所示，最下方的可靠度曲線為失效閾值為60 μA時的可靠度曲線，依次排列，最上方的可靠度曲線為70 μA時的可靠度曲線。隨著閾值的提高，可以看出t0.9不斷增加，t0.9介于220 000小時(約為25.46年)至237 600小時(約為27.5年)。

4 結論

本文構建的維納過程可靠性模型，一是考慮到個體化差異，將維納過程中的漂移系數隨機化處理，并且建立了隨機變量阿倫尼烏斯模型，使較傳統未考慮個體差異而固定漂移系數的方法更符合實際；二是使用兩步極大似然估計方法，可以求解未知參數的估計值，克服傳統估計方法的局限性；三是對非線性數據的處理，c的估計值為1.495 1，顯然大于1，按照分類來說為凹退化，如果直接將漏電流的退化數據看成線性數據，則其評定的準確度必然大大下降，因此對數據進行線性化處理，使其更加符合維納過程的特性。