基于改進ACO-BP算法的彈藥貯存可靠性評估
劉 芳,王宏偉,宮 華,許 可
(1.沈陽理工大學 理學院, 沈陽 110159; 2 遼寧華興機電有限公司, 遼寧 錦州 121017)
可靠性是彈藥產品質量的關鍵指標,是彈藥產品在戰斗中完成任務的核心保障。和平時期,彈藥產品長期處于貯存狀態,如何評估彈藥產品在貯存狀態下的可靠性是各國軍隊亟待解決的重要問題。長期以來,國內外學者對彈藥貯存可靠性的評估方法進行了大量研究。傳統的彈藥貯存可靠性評估方法主要以建立Bayes模型、Possion模型、隨機濾波模型和馬爾可夫模型等數理統計模型為主[1-5]。這些方法在使用中通常需要樣本的先驗分布類型,而彈藥產品的特殊性使其先驗分布又難以獲得,導致這些方法不能很好的應用于實際問題。近幾年,許多學者將BP網絡、局部逼近 RBF網絡、支持向量機、粒子群等智能算法引進可靠性的評估與預測,做了一些初步嘗試[6-12]。智能評估算法不需要預先知道樣本的先驗分布信息,能夠基于歷史數據直接評估和預測彈藥可靠性。但由于神經網絡訓練速度慢,且容易陷入局部最小和支持向量機算法對缺失數據的極端敏感性,使得將智能算法應用于可靠性研究中還有很多問題需要解決。
本文提出的兩種智能算法優化模型:自適應蟻群優化BP神經網絡彈藥貯存可靠性評估模型(AACA-BP)和精英蟻群優化BP神經網絡彈藥貯存可靠性評估模型(EACO-BP),采用不同的蟻群優化策略智能選取BP網絡的初始權值和閾值,解決了BP網絡易陷入局部最優和收斂速度慢的問題。AACA和EACO算法對傳統蟻群算法(ACO)的信息素更新策略均進行了改進與提升。
1 蟻群算法和BP神經網絡
1.1 蟻群(ACO)算法
傳統的蟻群算法是模仿螞蟻在尋找食物中搜索最優路徑的策略創建的群智能優化算法。螞蟻在覓食過程中,在經過的路徑上殘留一種稱為信息素的物質。跟隨螞蟻通過辨別前方路徑上信息素濃度的含量,選擇信息素濃度最高的路徑繼續前行,最終以最短路徑的方式到達食物所在地。蟻群算法描述了螞蟻覓食的信息積累和傳遞的優化機制,通過個體之間的信息交流與相互協作作為反饋機制獲得全局最優解。
蟻群算法的兩個核心策略分別為螞蟻擇路策略和信息素更新策略。螞蟻擇路策略描述了螞蟻如何選擇下一步經過的路徑,如式(1)。信息素更新策略描述了螞蟻在覓食了一段時間后路徑上的信息素更新方案,如式(2):
(1)
ηj(t+τ)=(1-μ)ηj(t)+Δηj
(2)
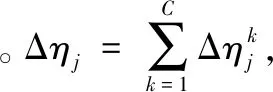
1.2 BP神經網絡
BP神經網絡是一種前饋人工神經網絡,它通過信息的正向傳遞與誤差的反向傳播,實現從輸入空間到輸出空間的高度非線性逼近。彈藥貯存可靠性的歷史數據與彈藥現場數據構成一個時間序列,存在隱含的非線性關系。神經網絡所具有的聯想記憶、非線性和良好的泛化與容錯能力,能夠挖掘彈藥可靠性歷史數據和現場數據之間的非線性函數關系,為可靠性的評估與預測提供了算法支持。本文采用由輸入層(m個節點)、隱含層(h個節點)和輸出層(l個節點)構成的m×h×l的3層網絡拓撲結構。網絡適應度函數:
(3)
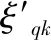
2 兩種改進蟻群算法
傳統蟻群算法有兩方面缺欠有待改進。一方面是傳統蟻群容易陷入局部最優;另一方面是收斂速度慢。本文采用自適應蟻群和精英蟻群兩種改進蟻群算法解決以上兩方面問題。每種算法在全局最優解的搜索策略和收斂速度兩方面均做了改進與提升。
2.1 自適應蟻群AACA
自適應蟻群在傳統的蟻群方法的基礎上,將信息素更新統一模式更改為局部信息素更新與全局信息素更新相結合的模式。螞蟻在探尋路徑中,根據自身的情況,不斷調整對路徑的選擇,最終尋得最短路徑。其中,信息素局部更新方案如式(4)所示。信息素全局更新方案如式(5)所示:
ηij=(1-ε)·ηij+ε·η0
(4)
(5)
式(4)中,ηij表示螞蟻從地點i走到地點j這條路徑上的信息素量,η0表示初始的信息素量。ε是一個常數,范圍在0~1之間。式(5)中,L*表示當前最優路徑的長度。
在信息素局部更新策略中,增加了初始信息素的調節功能。傳統蟻群算法中每條路徑的初始信息素濃度設置為同一數值,每條路徑初始被選擇的可能性是等概率的。這種路徑搜索方案會出現最優路徑在初始幾次循環信息素累計較少而降低其被選擇的可能性。增加的初始信息素信息,縮小了不同路徑上信息素濃度的差距,提升了信息素濃度少的路徑被選擇的可能性,避免算法陷入局部最優。在信息素全局更新策略中,只對當前狀態下最優路徑上的信息素進行更新。通過引進u/L*的增量,進一步增加了最優路徑的信息素濃度,提高了當前最優路徑在下次被選擇的概率,加速了算法收斂速度。
2.2 精英蟻群EACO
精英蟻群通過改進傳統信息素的更新模式和限定信息素濃度的方式實現了算法速度和全局搜索能力的提升。
精英蟻群對路徑上信息素濃度設置上下界[τmin,τmax]。當某條路徑的信息素濃度超過τmax或者低于τmin時,這條路徑的信息素量會被強制地限定為τmax或者τmin。信息素濃度限定策略可以有效地減少某條路徑的信息素濃度過大或者過小,降低算法陷入早熟的可能性,避免算法陷入局部最優。在信息素更新策略方面,螞蟻在完成一次路徑選擇循環后,根據螞蟻的種類更新信息素濃度。找到最優路徑的螞蟻定義為精英螞蟻。精英螞蟻走過的路徑信息素濃度額外增添一個與精英螞蟻個數有關的增量。這樣可以讓螞蟻在下次路徑選擇中能夠更多選擇當前最優的路徑,提高收斂速度。信息素更新公式如下:
ηij(t+τ)=(1-u)·ηij(t)+Δηij(t)+Δηij(t)*
(6)
(7)
Δηij(t)*表示精英螞蟻額外增添的信息素的量。精英螞蟻的個數記作g。
3 改進蟻群優化BP神經網絡算法
BP神經網絡初始權值和閾值的隨機性是導致評估結果不穩定的一個主要因素。本文采用兩種改進的蟻群優化BP神經網絡算法(AACA-BP和EACO-BP),將BP神經網絡的權值和閾值作為待優化的參數,通過蟻群的擇路策略和信息素更新策略最終獲得最優化的網絡初始權值與閾值的集合,有效提高了BP神經網絡評估的精度和穩定性。算法具體過程如下:
步驟1:對訓練樣本數據集和測試樣本數據集進行歸一化處理。
(8)
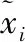
步驟2:建立m×h×l三層網絡拓撲結構。
步驟3:初始化蟻群參數。
步驟4:啟動螞蟻,自適應蟻群根據式(4)和式(5)方案更新信息素濃度,精英蟻群根據式(6)和式(7)方案更新信息素濃度。
步驟5:重復步驟4,直到所有螞蟻都選擇同一條路徑或者達到最大迭代次數為止,轉為步驟6。
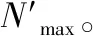
步驟7:將測試數據進行反歸一,還原測試數據形態。
(9)
4 仿真實驗
4.1 數據集
本文選取某彈藥在2014—2018年內在同一地點、同一貯存條件下的4個季度的可靠度統計數據作為實驗數據,如表1所示。
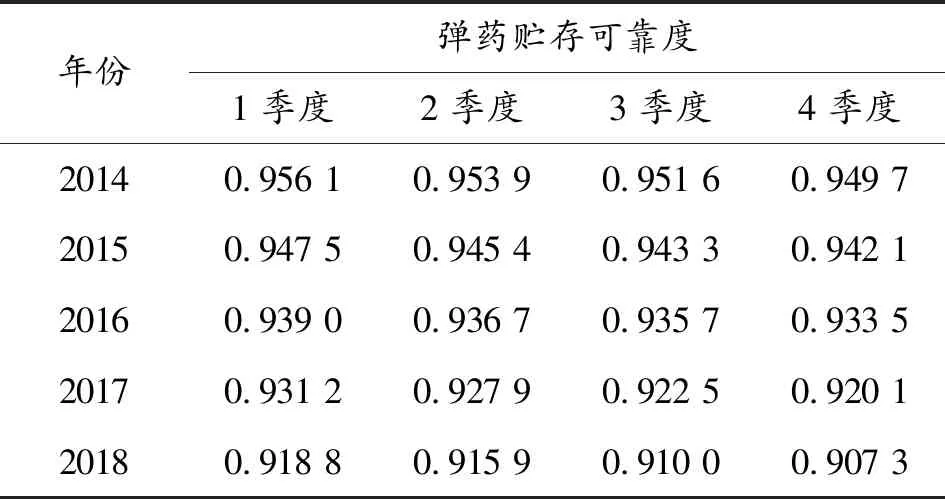
表1 彈藥貯存可靠度統計數據
以連續4個季度的數據作為輸入數據,下一季度數據為輸出數據,構建BP網絡輸入和輸出數據集,如表2所示。
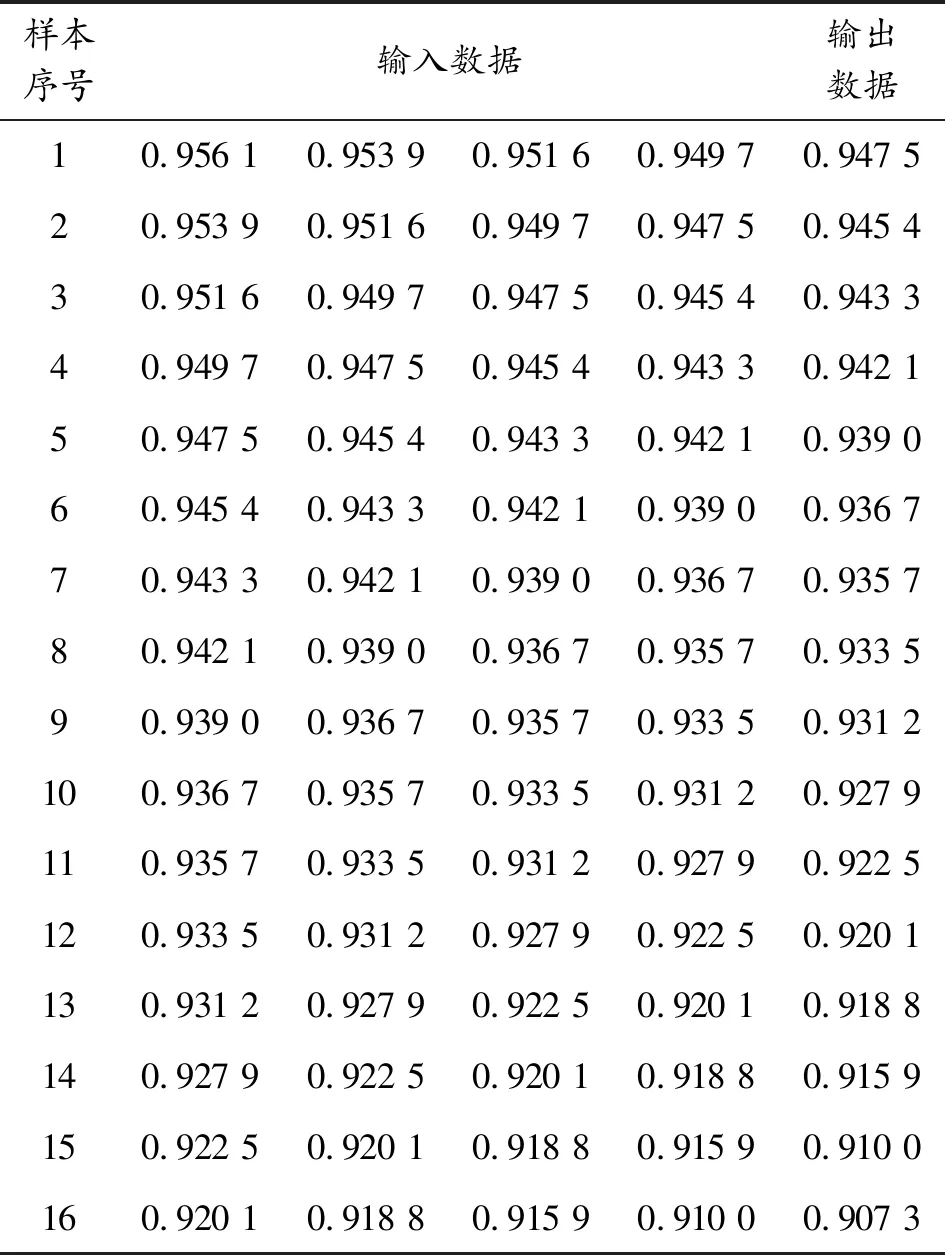
表2 BP網絡輸入與輸出
4.2 數據擴充
數據集中統計的數據僅為5年彈藥可靠性數據,樣本容量小。神經網絡作為一種學習機器,能否對新的例子做出正確反應,與訓練集給出的問題的信息量有直接關系。本文采用增加噪音信號的方法對樣本進行擴充處理。處理后的訓練樣本數量相比擴充前增加15倍,顯著提升訓練集的信息含量和質量,能夠有效提高網絡的評估精度和泛化能力。
具體操作如下:對網絡輸入數據增加噪音,輸出數據保持不變。設向量(x1,x2,x3,x4)為輸入數據向量,xi(i=1,2,3,4)表示輸入向量中的第i個分量。δi為增加的噪音值,取值為0.000 1。分別對向量(x1,x2,x3,x4)中任意一個xi、任意兩個不同的xi、任意3個不同的xi和4個xi加上δi,經過四步擴充后,每一樣本被擴充成16個不同樣本,原始16個樣本被擴充為256個樣本。
4.3 參數設置
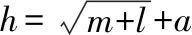
BP神經網絡的目標誤差設為0.000 01。學習效率為0.1。迭代次數設為1 000。 BP網絡隱含層激勵函數為tansig, 輸出層的激勵函數為purelin,網絡訓練函數選取trainlm。改進蟻群待優化的BP神經網絡的權值和閾值參數維度為37,每個參數值在[-1,1]中隨機取20個數值,螞蟻數量為60,信息素初始值設為1,信息素揮發系數取0.1、蟻群最大迭代次數設為800。
選用MATLAB 2016a編程工具編制m文件分別對基于BP算法、ACO-BP算法、AACA-BP和EACO-BP算法的彈藥貯存可靠性評估模型進行仿真實驗,對結果進行分析。
4.4 算法性能對比
本文分別對四種智能算法進行了精度、穩定性和速度的性能對比仿真實驗。為了避免實驗結果的偶發性,在對每種智能算法的各種性能比較中,均采用了隨機抽取的10次試驗結果的均值作為參考數據。
由表3可見,AACA-BP和EACO-BP算法求解的可靠度的精度明顯高于單獨BP算法和ACO-BP算法。兩種改進蟻群算法優化BP模型中,EACO-BP算法計算出的期望可靠度與實際可靠度的均方誤差均值相對于AACA-BP降低3.8%。這說明EACO-BP算法在彈藥可靠性評估中比AACA-BP算法評估的可靠度精度略高。由表3的迭代次數統計中可見,AACA-BP和EACO-BP算法的迭代次數明顯少于BP算法和ACO-BP算法的迭代次數。AACA-BP算法分別比BP算法和ACO-BP算法迭代次數減少47.5%和34.375%。 EACO-BP算法分別比BP算法和ACO-BP算法迭代次數減少70%和62.5%。兩種改進蟻群算法優化BP模型中,EACO-BP算法的迭代次數相對于AACA-BP降低了42.86%。由圖1可見,AACA-BP算法與EACO-BP算法的評估曲線比BP網絡曲線的波動性小,算法穩定性好。AACA-BP算法比EACO-BP算法更穩定。
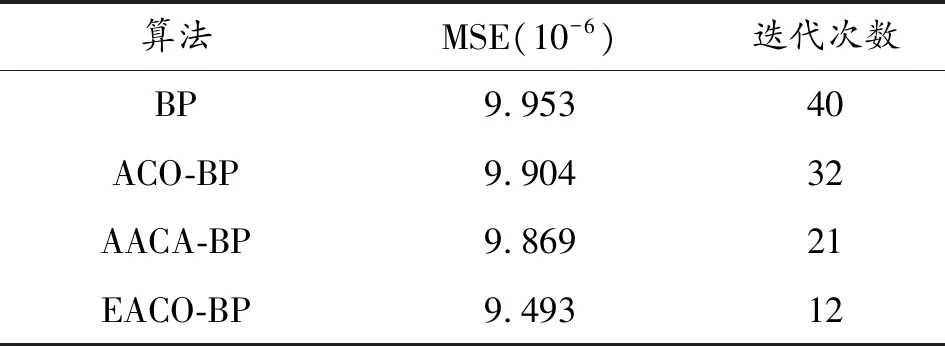
表3 四種智能算法精度與迭代次數

圖1 4種算法期望可靠度與實際可靠度均方誤差曲線
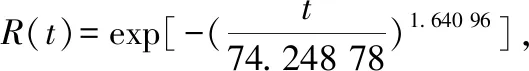
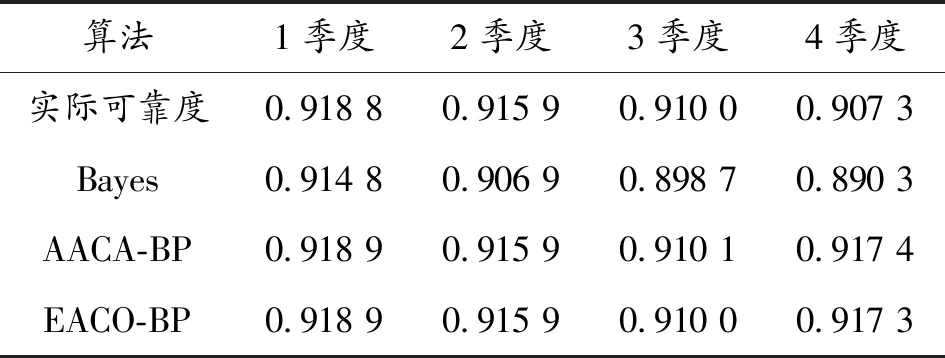
表4 2018年4個季度的可靠度數據對比
5 結論
1) 提出了兩種彈藥貯存可靠性評估算法:AACA-BP和EACO-BP算法。通過彈藥歷史數據評估彈藥現場數據。在AACA算法和EACO算法中,采用了不同的信息素更新策略,解決了傳統蟻群算法易陷入局部最小和收斂速度慢的問題。
2) 由兩種改進蟻群優化BP網絡的權值和閾值具有更好的網絡評估性能,提高了單獨BP神經網絡評估彈藥可靠度的精度和穩定性,減少了迭代次數。EACO-BP算法在評估的精度和迭代次數方面優于AACA-BP,而AACA-BP算法穩定性能比EACO-BP算法更高。
3) 兩種彈藥可靠性評估方法均可推廣應用于具有歷史數據或者影響因素的各種可靠性評估問題,為可靠性評估研究提供了一種新的智能途徑。

