一種粒子群優化的SVM-ELM模型*

王麗娟，丁世飛

1.中國礦業大學 計算機科學與技術學院，江蘇 徐州 221116

2.徐州工業職業技術學院 信息與電氣工程學院，江蘇 徐州 221140

1 引言

極限學習機（extreme learning machine,ELM）是一種簡單、有效的單隱層前饋神經網絡SLFNs學習算法[1]。只需設置網絡的隱含層節點個數，在算法執行過程中，輸入權值、隱含層偏置采取隨機賦值的方式，通過最小二乘法得到輸出層權值，產生唯一的最優解。由于ELM是基于經驗風險最小化原理，隨機輸入權重和隱含層偏置，可能會導致部分隱含層節點無效[2]。因此ELM分類正確率的高低取決于隱含層的節點數，需要大量的隱含層節點來保證分類的精確度。和傳統的基于梯度下降的學習算法相比較，由于ELM需要更多的隱含層神經元，這就降低其運算速率以及訓練效果，為此人們提出了許多ELM的改進算法。

Huang等人基于遞歸最小二乘法（recursive least square，RLS)，提出了在線時序極限學習機（online sequential ELM，OS-ELM）算法[3]。之后，又提出了一種在線連續模糊極限學習機（online sequential-fuzzy-ELM，OS-Fuzzy-ELM）模型來解決函數逼近和分類的問題[4]。Rong等人針對原始的極限學習機由于分類網絡的結構設計而導致的模式分類的低度擬合/過度擬合問題，提出了修剪極限學習機（pruned-ELM，P-ELM）作為ELM分類網絡系統化和自動化的方法[5-6]。Silva等人對極限學習機進行了改進，提出利用群搜索優化（group search optimizer，GSO）戰略選擇輸入權值和隱含層偏置的ELM算法，稱為GSOELM方法[7]。這些優化方法，和ELM相比，都得到了很好的分類效果[8]。

20世紀90年代初，文獻[9-10]提出支持向量機（support vector machine，SVM）。該算法建立在統計學習理論的基礎之上，根據結構風險最小化原則提出的[11-12]，比神經網絡更適合于小樣本的分類，且泛化性能出色[13-14]。在模式識別、回歸分析、函數估計、時間序列預測等領域都得到了發展，并被廣泛應用于手寫字體識別、人臉圖像識別、基因分類等領域[15]。SVM通過核函數把低維空間的線性不可分問題轉化為高維空間的線性可分問題，構造最優分類面，實現對數據樣本的分類[15]。

ELM分類正確率的高低取決于隱層的節點數，但是大量的隱層節點使得ELM的結構很臃腫，而且容易導致內存不足。為了提高ELM單個節點學習能力和判斷能力，本文利用支持向量機（SVM）來精簡ELM，通過構建SVM-ELM模型，提高單個節點的判斷能力。傳統的參數選取都是經過反復的實驗，憑借經驗值來選取的，存在著很大的主觀性；如果通過交叉驗證的方式來選取參數，又會消耗大量的時間。本文為了使得SVM-ELM模型獲得較好的分類準確率，利用PSO算法進行優化[16]，實現分類目標。

2 SVM-ELM模型

極限學習機（ELM）是2004年由南洋理工大學黃廣斌教授提出，是單隱層前饋神經網絡（single hidden layer feedforward neural network，SLFN）的一種[17-18]。傳統的ELM算法隨機確定隱層節點的權值wi和偏置bi，從實驗結果來看，這種方法大幅度地節省了系統的學習時間，但是如果想要獲得較好的分類效果，需要大量的隱層節點，而較少的節點則導致分類效果較差。這就表明，單個隱層節點的學習能力和判斷能力不足，需要較多的節點來彌補，而節點的學習能力不足則是由于節點的線性決策函數的權值和偏置值隨機決定造成的，使得節點欠學習[19]。如果能夠提高ELM單個隱層節點的學習能力，那么即使較少的隱層節點也能獲得較好的學習效果，ELM的網絡結構就得以優化。SVM通過尋求結構化風險最小來提高泛化能力，基本思想是尋找最優分類面，使正、負類之間的分類間隔（margin）最大[20]。

由于ELM經驗風險最小，以訓練誤差最小的準則來評價算法優劣，容易出現過擬合現象，影響分類模型泛化能力；一個好的分類模型在考慮結構風險和經驗風險的同時還要對二者合理優化平衡，從而保證分類模型的泛化能力。本文將結構風險最小化的支持向量機（SVM）引入到極限學習機（ELM）中，提出一種ELM和SVM相融合的分類模式[21]。選取ELM為基礎分類器，以SVM來修正改善分類效率。利用SVM來提高每個節點的判斷能力，精簡ELM的結構，提高其泛化性能。根據分類的類別數來確定層的節點數，改變傳統的隨機確定的方式，然后利用SVM來確定每個隱層節點的權值和偏置[22]，提高每個節點的學習能力和泛化能力。對于k類分類問題，SVMELM的隱層節點數為k，第i個節點的任務就是，利用SVM把第i類與其他的k-1類分開，根據SVM得到的訓練結果得到每一個隱層節點的權值和偏置。

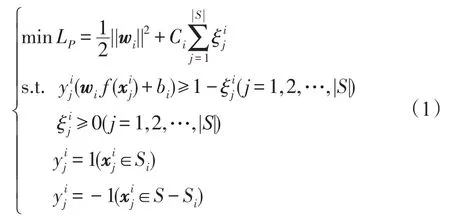
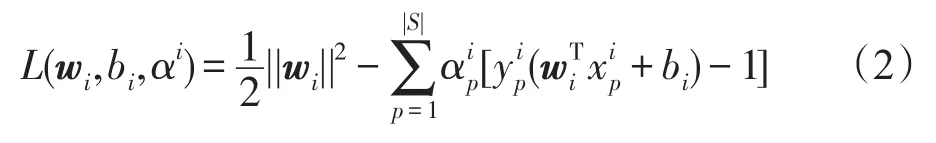
式（1）的對偶問題為：

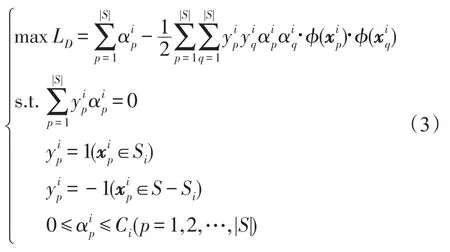
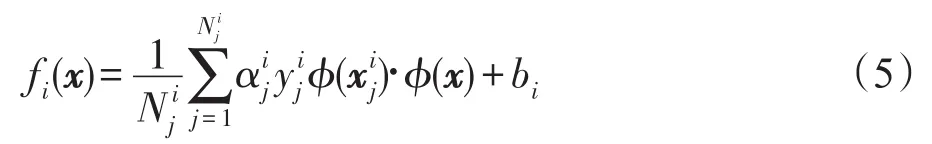
隱含層的輸入矩陣表示為：

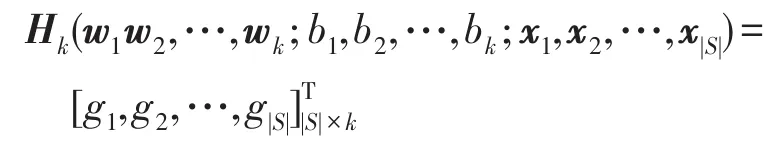
其中：

故：

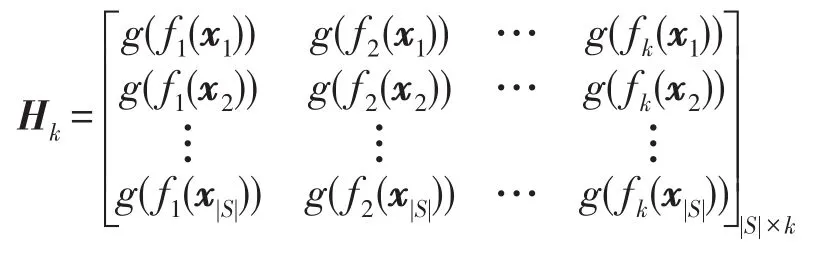
其中，g(x)為ELM的激活函數。ELM常用的激活函數有Sigmoid函數、Sine函數、RBF（radialbasisfunction）函數等。本文選用效果較好的Sigmoid函數。則隱層節點數為k、激勵函數為g(x)的SLFN模型為：

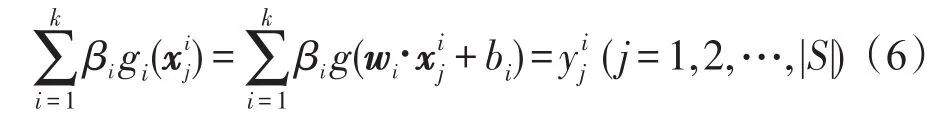
即學習系統為Hkβk=Y，學習參數：

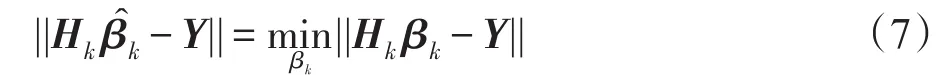
3 基于粒子群優化算法的SVM-ELM

文獻[23]提出了粒子群優化算法（particle swarm optimization，PSO），該算法是一種啟發式隨機優化算法，在有限的迭代遞推中快速搜索到全局最優解，該特性已被廣泛地應用于數據挖掘和模式識別［20］等領域。支持向量機的參數選擇直接影響到SVM模型的分類結果[24-26]。即使對于同一個分類問題，選擇不同的SVM模型核函數、懲罰參數都將產生不同的分類結果。在實際應用中，為了獲得性能更高的SVM分類器，則需要對SVM的各個參數進行優化調整[27]。因此，本文提出一種PSO-SVM算法，使用粒子群優化算法和支持向量機相結合的學習算法，即利用PSO算法的全局搜索能力對SVM的懲罰參數和核函數參數的取值進行優化調整[23]，避免選擇局部最優的參數，使SVM的參數取值更具指導性，從而得到一個更精確的、分類效果優化的SVM分類器。文獻[28-30]中闡述了PSO算法比人工神經網絡（artificial neural network，ANN）、遺傳算法（genetic algorithm，GA）實現更簡單，使用參數更少。

基于PSO全局搜索對SVM參數全局尋優的PSO-SVM-ELM模型訓練流程圖如圖1，詳細處理步驟如下：

步驟1數據預處理。優化算法通過已知數據集隨機產生訓練集和測試集進行訓練來獲得SVM模型。

步驟2初始化粒子群的粒子數、最大迭代次數、每個粒子的初始位置、速度初值、個體最優位置和全局最優位置等，以及SVM的參數C和RBF核函數的寬度參數σ。

步驟3通過交叉驗證算法PSO在全局空間搜索粒子最優解，獲得SVM模型懲罰參數、核函數參數的最優值。

步驟4將訓練數據集帶入SVM訓練得到PSOSVM訓練模型。

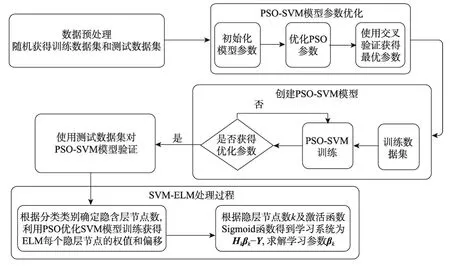
Fig.1 PSO-SVM-ELM model flowchart圖1 PSO-SVM-ELM模型流程圖

步驟5用測試數據集驗證PSO-SVM模型的處理能力，得到優化了的PSO-SVM模型。

步驟6根據分類類別確定隱含層節點數，利用PSO-SVM模型訓練，獲得ELM每個隱含層節點的權值和偏移。

步驟7根據隱含層節點數k及激活函數sigmoid函數得到學習系統模型，求解學習參數。

步驟8獲得高精確度的分類模型PSO-SVMELM。

其中，利用PSO算法優化SVM參數的詳細過程如圖2，詳細步驟為：

步驟1獲得訓練數據集，組建粒子群；設置SVM參數搜索范圍。

步驟2初始化粒子群參數包括粒子數量、最大迭代數、粒子群初始位置和速度初值以及每個粒子個體位置最優pbest和群體位置最優gbest等，初始化SVM模型參數C和RBF核函數的寬度參數σ。

步驟3更新pbest和gbest并記錄粒子的適應值。

步驟4更新粒子群中粒子的位置和速度。

步驟5若達到最大迭代次數或找到最優解，則算法結束，轉向步驟6，否則轉向步驟2，繼續求解。

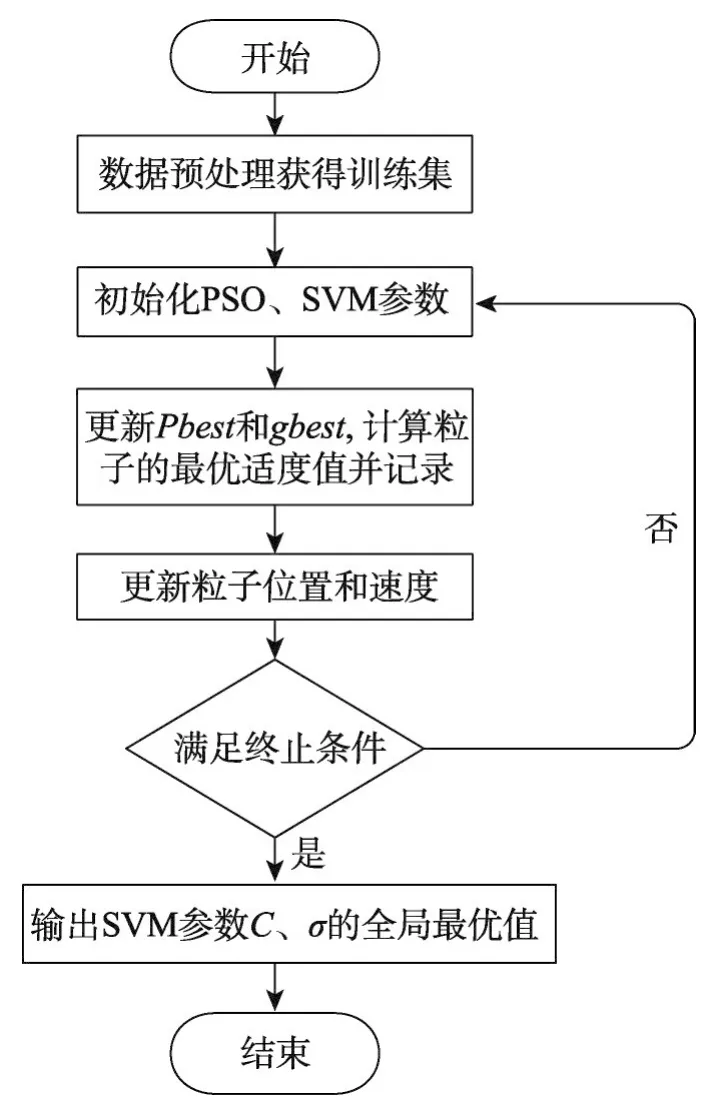
Fig.2 PSO-SVM model flowchart圖2 PSO-SVM模型流程圖

步驟6輸出SVM模型的懲罰參數C和RBF核函數的寬度參數σ的全局最優值，算法結束。

利用粒子群優化算法對SVM-ELM模型中的參數進行自動選擇，克服了人為選擇的主觀性，避免了人為嘗試浪費過多的時間，同時通過設置粒子適應度函數可以實現控制參數選擇的方向的目的[31-33]。

4 實驗分析

為了驗證基于粒子群算法的SVM-ELM模型的有效性，從UCI機器學習數據庫中選取了4個用于分類的數據集葡萄酒質量數據集Wine、小麥種子數據集Seeds、Balance Scale以及CNAE-9進行實驗，數據描述如表1所示。

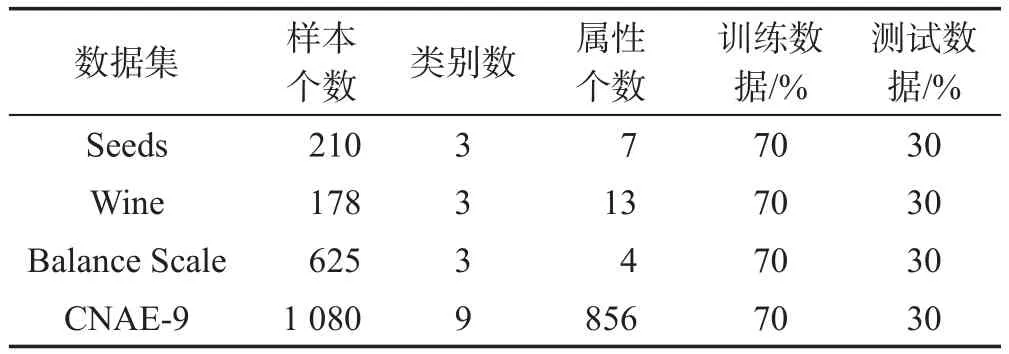
Table 1 Description of data sets表1 數據集描述

在SVM-ELM模型中，運用SVM模型求解過程來優化ELM隱含層節點的權值和偏置時，SVM的核函數有多種：徑向基核、多層感知器核等。根據實驗結果，本文選擇了徑向基核函數，即；ELM激活函數選擇性能較好的Sigmoid函數，即g(x)=1/(1+e-x)。

基于粒子群算法的SVM-ELM模型中，待優化的參數為RBF核函數的寬度參數σ、懲罰參數C。這三類數據集的種群大小以及參數搜索范圍的取值如表2所示。

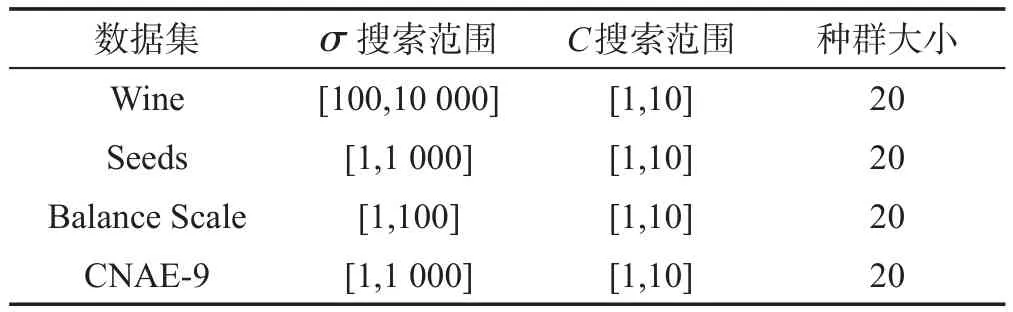
Table 2 Value of PSO parameters表2 PSO參數的取值

粒子群的加速因子c1=c2=2，種群的規模m=20，慣性權重w=0.9，最大迭代次數為2 000。實驗環境：Intel?Xeon?CPU E3-1225 V2@3.20 GHz處理器，4 GB RAM，32位操作系統，Matlab R2012b。PSO算法在經過多次迭代之后，每個數據集獲得的參數σ和C如表3所示。

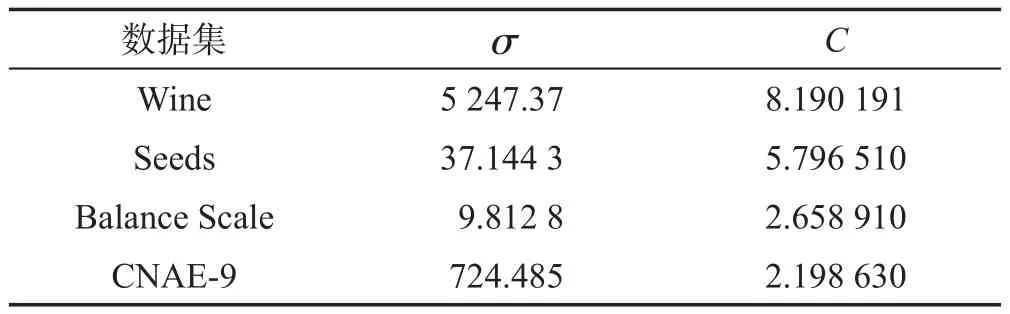
Table 3 Parameter value of PSO-SVM-ELM model表3 PSO-SVM-ELM模型參數值

數據集 Wine、Seeds、Balance Scale、CNAE-9 的gbest值隨著飛行路徑的變化分別如圖3～圖6所示。從圖中可知針對這4個數據集，PSO算法具有較強的收縮能力，都能最終找到全局最優值，可以有效地解決SVM參數優化問題。

Fig.3 Flight trace of global optimal value of Wine data set圖3 Wine數據集全局最優值的飛行路徑

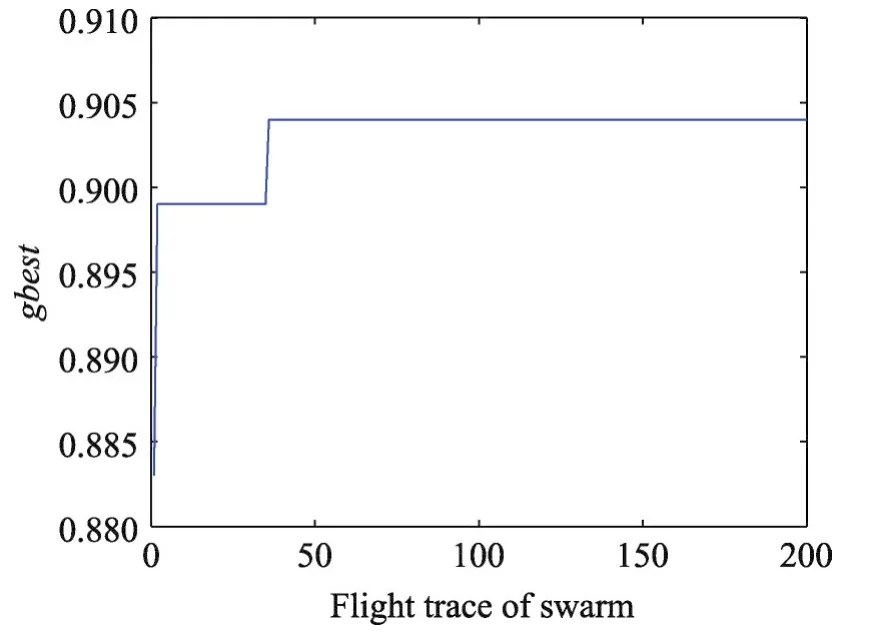
Fig.5 Flight trace of global optimal value of Balance Scale data set圖5 Balance Scale數據集全局最優值的飛行路徑

基于粒子群優化的SVM-ELM模型的分類結果如表4所示。

Table 4 Classification results of PSO-SVM-ELM model表4 PSO-SVM-ELM模型的分類結果

通過不斷的嘗試、實驗，根據分類效果確定SVMELM模型的參數。Wine、Seeds、Balance Scale數據集均有3類數據，故這3類數據集的SVM-ELM模型的隱層節點數均為3。而CNAE-9數據集的數據類別為9，故隱層節點數為類別數9。SVM-ELM分類結果如表5所示。

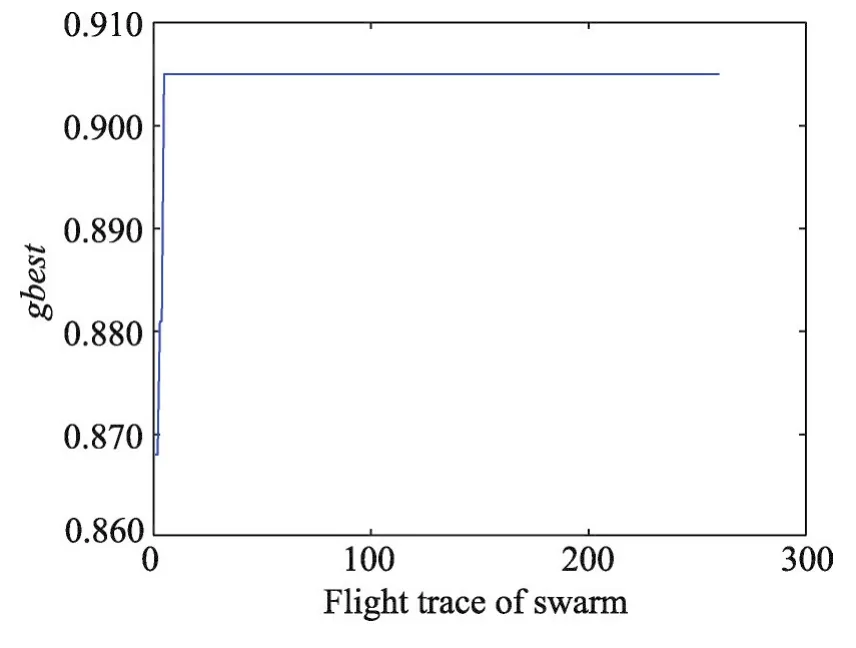
Fig.4 Flight trace of global optimal value of Seeds data set圖4 Seeds數據集全局最優值的飛行路徑

Fig.6 Flight trace of global optimal value of CNAE-9 data set圖6 CNAE-9數據集全局最優值的飛行路徑

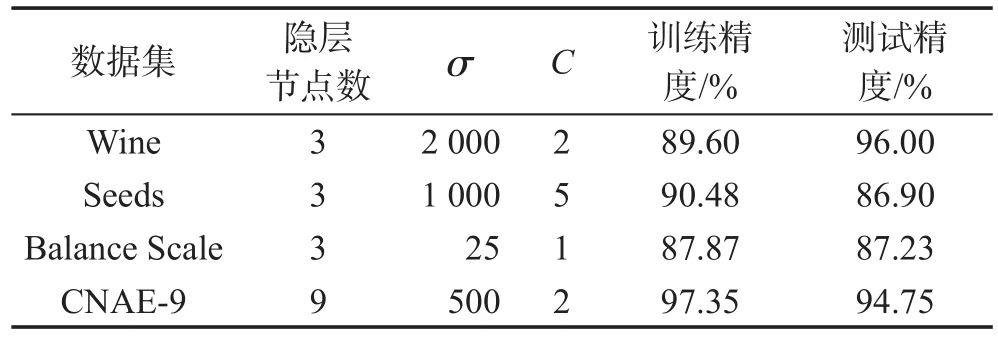
Table 5 Experimental results of SVM-ELM表5 SVM-ELM的實驗結果

在設置不同的隱層節點數的情況下，ELM的分類結果如表6所示。表6中所列出的數據是在隱層節點數確定時，重復10次實驗，選擇其中測試精度的最大值作為最優值。

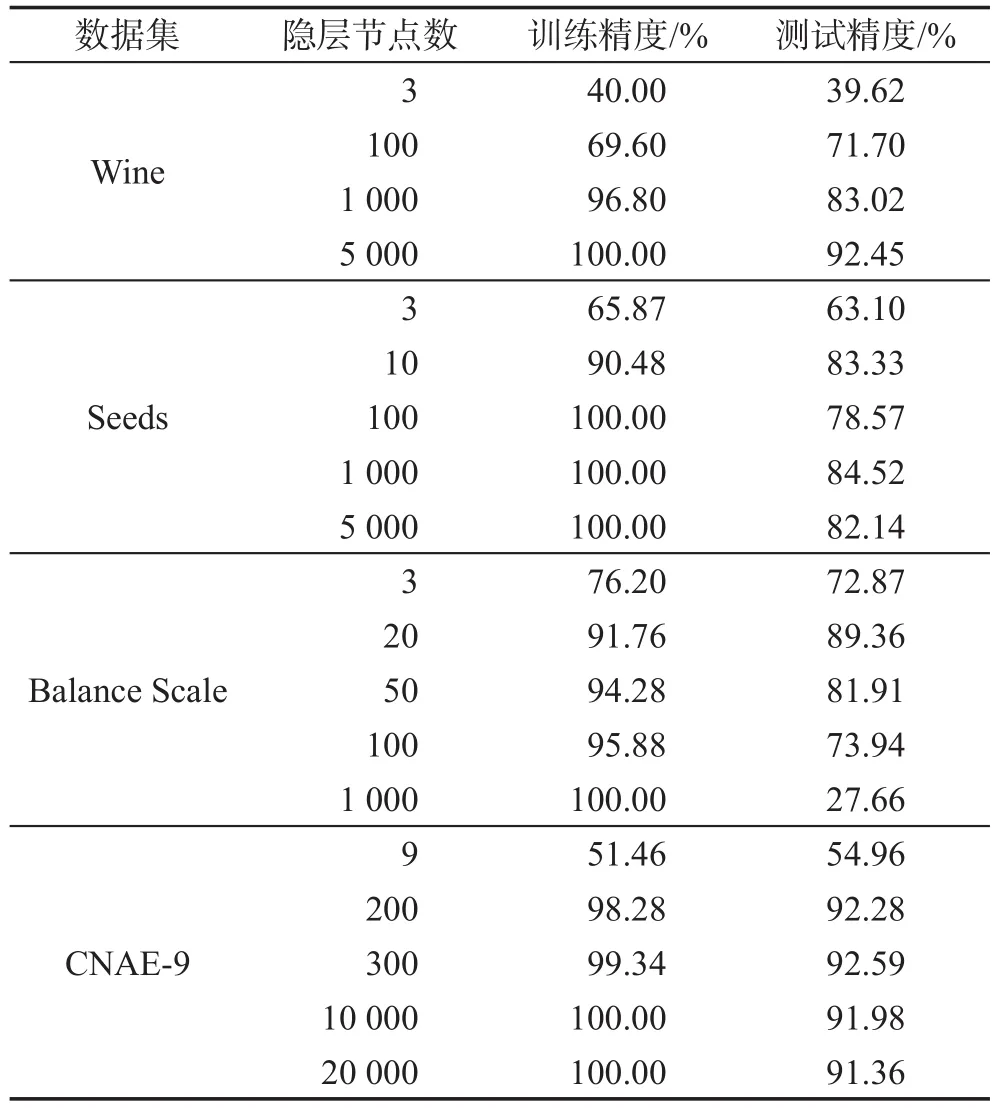
Table 6 Experimental results of ELM表6 ELM的實驗結果

在Wine數據集上，隨著隱層節點數的增多，ELM的測試精度不斷提高；在Seeds、CNAE-9數據集上，隨著隱層節點數目的增多，ELM的測試精度出現局部的波動，但整體依然是不斷提高的。這表明ELM的學習效果和隱含層的節點數有很大的關系，要想達到良好的學習效果，必須有足夠多的隱層節點，導致網絡規模很臃腫。在Balance Scale數據集上，隨著隱層節點數目的增多，ELM的測試精度出現先逐漸提高，然后下降的情況，這說明ELM的穩定性較差，且容易出現過擬合的現象。

比較表4～表6可以發現，本文提出的PSO-SVMELM模型在這4個數據集上的測試精度均高于SVM-ELM和ELM。其中在Wine數據集上，PSOSVM-ELM的測試精度高于SVM-ELM模型的測試精度2.11%，高于ELM的最高精度5.66%；在Seeds數據集上，PSO-SVM-ELM的精度高于SVM-ELM模型的測試精度3.58%，高于ELM的最高精度5.96%。PSO-SVM-ELM、SVM-ELM和ELM對于所選取的數據集的分類正確率的比較如表7所示。

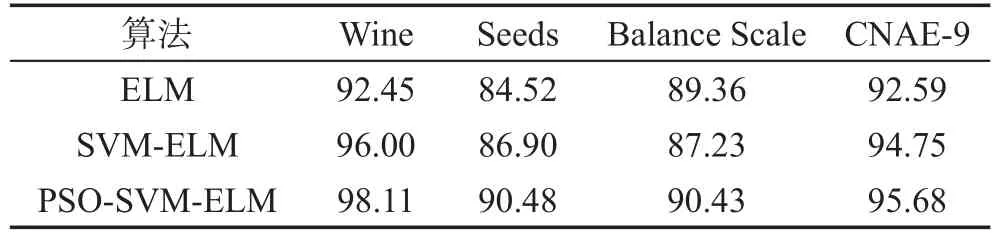
Table 7 Comparison of experimental results表7 實驗結果對比 %

SVM-ELM的參數確定經過了多次的嘗試，浪費了大量的時間，并且沒有找到最優值。而ELM達到最高精度的隱層節點數分別為5 000、1 000、20、300，也經歷了無數次的嘗試。ELM的結果極不穩定，且容易出現過擬合的現象。而PSO-SVM-ELM的隱層節點數僅僅為數據集中的數據類別數，網絡穩定，不會出現過擬合的現象，并且可以很方便地就可以找到最優值。

5 結論

本文提出了基于粒子群算法優化的SVM-ELM模型，即PSO-SVM-ELM模型，通過SVM確定ELM的隱層節點的權值和偏置，然后利用粒子群算法（PSO）來優化SVM-ELM的參數。PSO-SVM-ELM模型在提高極速學習機的泛化性能的同時精簡了ELM，使得在隱層節點數為待分類數據集的類別數時，能夠達到很好的分類效果，實驗足以說明基于粒子群優化的SVM-ELM模型在進行數據分類時是比較理想的。