Particle–hole f luctuationsand possible superconductivity in dopedα-RuCl3*
Bin-BinWang(王斌斌),WeiWang(王巍),Shun-LiYu(于順利),2,?, and Jian-Xin Li(李建新),2,?
1National Laboratory ofSolid State M icrostructuresand DepartmentofPhysics,Nanjing University,Nanjing 210093,China
2Collaborative Innovation CenterofAdvanced M icrostructures,Nanjing University,Nanjing 210093,China
(Received 30 January 2019;revisedmanuscript received 19March 2019;published online4April2019)
Keywords:superconductivity,particle–hole f luctuations,spin–orbitcoupling,α-RuCl3
1.Introduction
The doped Mott insulators[1–6]have been subject to extensive investigations because they contain plentiful phases,such as spin-density wave(SDW),pseudogaps,and superconductivity.In parentcompounds,the charge insulation ofmost Mott insulators raises solely from the Coulomb interaction.However,recently a new fam ily of Mott insulator,in which the charge insulation is resulted from the cooperative interplay between spin–orbit coupling(SOC)and electron correlation,hasbeen proposed,such asSr2IrO4,[7,8]Na2IrO3,[9–11]andα-RuCl3.[12–14]In theseMott insulators,the electron conf iguration for theactive ions isd5,such as5d5of Ir4+in iridatesand 4d5of Ru3+in ruthenium.Within the octahedral crystal f ield,the d orbitalsaresplit into a two-fold egmanifold and a threefold t2gmanifoldwithaneffective leff=1orbitalmoment.The latterare further divided into a fully f illed jeff=3/2 band and a half-f iled jeff=1/2 narrow band by strong SOC.Then the jeff=1/2 band only needs amoderate electronic correlation to open a Mott gap.Thus these Mott insulators are usually referred to asspin–orbitassisted Mottinsulators.
The novel physics of these jeff=1/2 Mottmaterials in different lattices has been reported both experimentally and theoretically.For thesquare lattice,acanted antiferromagnetic structure has been found in Sr2IrO4,[15–17]which is isostructural to La2CuO4,a parent compound for cuprate superconductors.Sim ilar to the doped cuprate Mott insulator,pseudogap,Ferm iarc,[18–21]and superconductivity[22–26]are also addressed in doped Sr2IrO4.For the honeycomb lattice,an intriguing physics is that the Kitaev interactions underlying the celebrated Kitaev model,[27]whose ground state is exactly a Z2spin liquid with Majorana ferm ion excitations,can be realized.[28]In this aspect,the honeycomb-latticematerial α-RuCl3has recently attractedmuch attention.[12–14,29,30]Although the ground state ofα-RuCl3has a long-range zigzag magnetic order,abroad continuousspectrum in inelastic neutron scattering has been observed[12–14]and the magnetic order can be fully suppressed by either an in-plane magnetic f ield[31–33]or pressure.[34–36]There is accumulating evidence that the f ield-induced disordered state is a prom ising candidate as a quantum spin liquid.[31–33]For doped systems,the jeff=1/2 Mottmaterials with honeycomb lattice also exhibit many exotic physics,such as unconventional superconductivity[37–41]and unique charge dynam ics.[42–49]
In thispaper,based on themulti-band Hubbardmodel including all t2gorbitals,we investigate various particle–hole(PH)excitations and possible superconducting pairingsmediated by these f luctuations in the doped systems with the random-phase-approximation(RPA)method.We f ind that the jeff=1/2 pseudospin f luctuations dominate over the f luctuations from other particle–hole excitations,suggesting the robustness of the jeff=1/2 picture even in the doped systems,and themost favorable superconducting statemediated by the pseudospin f luctuationshasa d-wave pairing symmetry.
2.M ethod
The low-energy physicsofα-RuCl3is dominated by the t2gorbitalsdue to the4d5conf iguration of Ru3+and theoctahedral crystal f ield,so our calculations are based on the t2gthree-orbitalmodel,[30]which is derived through f itting the band structure from the density-functional theory(DFT).The three-orbitalHamiltonian isgiven as

where the parameters in the three-orbital tight-binding Ham iltonian Ht2gand SOC Hsocare from Ref.[30].Theband structure of this three-orbitalmodelwith SOC is shown in Fig.1.The interactionsbetween electronsare included in Hintas follows:

where U(U′)is the intra-orbital(inter-orbital)Coulomb interaction,Jhand J′are the Hund’s coupling and pairhopping,respectively.In thispaper,weemploy U=U′+2Jhand Jh=J′.
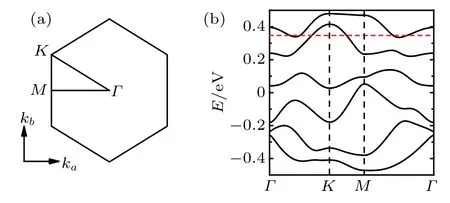
Fig.1.(a)Brillouin zone of the honeycomb lattice.(b)Band structure of the t2g three-orbitalmodelwith SOC forα-RuCl3.The horizontal red dashed line indicates the Ferm i level for theundoped system.
Based on the scenario that the pairing interaction arises from the PH f luctuations,we can calculate the effective electron–electron interactions using the RPA.However,as a result of the effect of the SOC,the effective particle–particle interaction cannot be simply divided into bubble and ladder diagramsas is the casewith SU(2)symmetry.[50]Thus,to include the SOC in the RPA approach,we use the Hugenholtz diagrams in our calculations.[20]In thismethod,the susceptibilities from the PH excitationsaregiven by

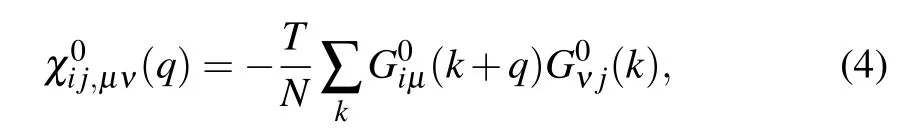

with the number of unit cell N and the temperature T.The bare Green’s function isw ritten as Here,the labels i,j,μ,andνinvolve all of the degrees of freedom(sublattice,orbital,and spin)in an unit cell.Thus,for the three-orbitalmodel on the honeycomb lattice,G is a 12×12matrix,whileχ,χ0,andΓare144×144matrices.In the above,k≡[k,iωn](q≡[q,iωm])withωn=(2n+1)πT(ωm=2mπT)for fermions(bosons).
The effective interaction in the particle–particle channel isgiven by[20]


Thegap function isderived from the linearized superconducting gap equation,which isgiven by Considering thatthedom inantscatteringsoccurnear the Ferm i surface(FS),we can project the effective pairing interaction(Eq.(6))and the gap equation(Eq.(7))on the FS.In this way,the scattering amplitude of a Cooper pair from the state(k,-k)on theγ1FS to the state(k′,-k′)on theγ2FS iscalculated by[51–53]
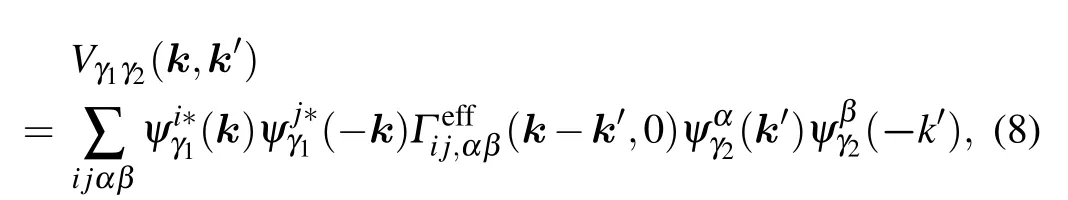
whereψiγ1(k)is theγ1-th eigenvector of theHt2g(k)matrix.We then solve the following linearized gap equation:
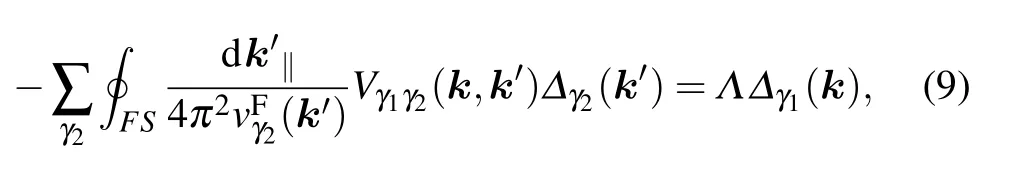
where vFγ2(k′)is the Ferm i velocity for bandγ2andΔγ1(k)represents the normalized gap function along the FSγ1.The integration and summation in Eq.(9)are along various FS patches.Here,the temperature is setat T=0.001 eV and the calculation of the susceptibility is donewith uniform 64×64 meshes in themomentum space.Thisequation can be solved as an eigenvalue problem,where the eigenvector corresponding to the largesteigenvalueΛdeterm ines the favourable pairing symmetry.
3.Resultsand discussion
Letus f irststudy themain propertiesof thePH excitations in theholedoped system.To f ind thedom inantPH excitations,we classify various PH channels according to the totalangularmomentum of a PH pair.Generally,the susceptibility can bew ritten in terms ofFαβ=d?αdβ;i.e.,χμν,αβ=FνμFαβ.To show the labels of the effective angularmomentums explicitly,we can express the annihilation operator of electrons as dζjm,where j and m indicate the quantum numbersof the totaleffectiveangularmomentum and its z component,respectively,ζcontains other quantum numbers except the angular momentum.Then,the PH excitation operators arew ritten as,which are tensoroperators.Since the representations of d?ζjmand dζjmare D1/2⊕D3/2in the sectorof effectiveangularmomentum,theoperator

has the follow ing decomposition in the sector of effective angularmomentum:Thus,the operatorF could be divided into irreducible tensor operatorsTj1j2jm(ζ1ζ2)asgiven in Appendix A.Here,j1and j2are the angularmomenta of the particle and hole.Therefore,including the sublattice indices on the honeycomb lattice,the susceptibilitiesχare split into 144×144 channelswhich include jeff=1/2excitations,jeff=3/2excitations,and various spin–orbit excitations between the jeff=1/2 and jeff=3/2 states.Among these channels,we f ind numerically that the jeff=1/2 pseudospin f luctuations Sη1η2(q)are dominant in the doping regime thatwe consider in the follow ing discussions.The jeff=1/2 pseudospin susceptibilities Sη1η2(q)are def ined as
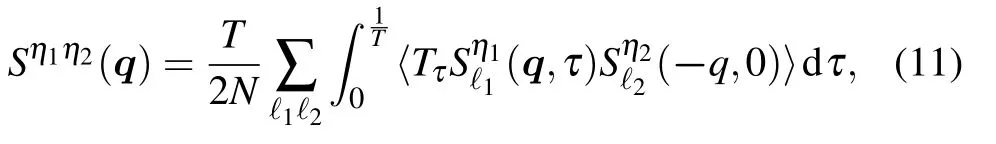
where?1and?2are the sublattice indices,and the pseudospin operators Sη?are given by

When the interactionsare increased,themagnitudesof pseudospin f luctuations are drastically enhanced in contrast to other typesof f luctuations.
In Figs.2(a)–2(c),weshow thediagonal(Sxx,Syy,Szz)and off-diagonal(Sxy)channels of the pseudospin susceptibilities togetherwith the largesteigenvalueofχalong theΓ–M–K–Γ path for thenumberofelectronsin primitive cell ne=9.8,9.7,and 9.6(in the parent compound,ne=10).It can be seen that the pseudospin Jeff=1/2 susceptibilities capture nearly all features of the maximal eigenvalue of?χand also show comparable intensities.Thus,the jeff=1/2 picture is robust in the doping rangewe consider here.The differences of Sxx,Syy,and Szzshown in Figs.2(a)–2(c)are the ref lectionsof the asymmetry of the Kitaev exchange interaction in the weakcoupling lim it.Moreover,when rotating 120°clockw isealong kc-axis,the transformation of pseudospin f luctuations has a cycle rule:(x,y,z)→(y,z,x),namely,Sxx→Syy,Syy→Szz,and Szz→Sxx,which is also coincidentwith the symmetry of the Kitaev interactions.[27]In the undopedα-RuCl3,thematerial shows a zigzag magnetic order,which gives a peak of the susceptibilities at M point in the Brillouin zone.[14]Our results of the doped systems also show obvious peaks around the M point,which result from the zigzag magnetic f luctuations,though the static zigzag order for the undoped system(ne=10)can not be obtained in our calculations due to the divergenceof the RPA susceptibility.For ne=9.8(Fig.2(a)),the peaks of the susceptibilities deviate from the M point.When theelectron concentration isdecreased,the peaksmove to the M point again,meanwhile the intensities of the peaks are enhanced.In Figs.2(d)–2(f),we present the pseudospin susceptibility S(q)=∑ηSηη(q),from whichwecan seemore clearly thedistributionof thepseudospin susceptibilitiesin the whole Brillouin zone.
We then study the properties of superconducting pairing by solving Eq.(9).We f ind that themaximal values ofΛare in the pseudospin-singlet pairing channel and are far greater than thoseof the pseduospin-tripletpairing states.So,wew ill only discuss the superconducting pairing in the singlet channel.In Figs.2(g)–2(i),we present the real partsof the leading pairing gap functions for three different electron concentrations,which show basically a d-wave symmetry.To understand thedetail formsof thepairing gap functions,we try to f it the gap functions by including the electron pairings up to the third nearest-neighborsites in realspace.The f itting functions aregiven by

with
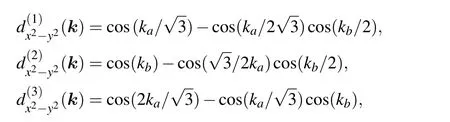

being the f irst,second,and third nearest-neighbor pairing functions,respectively,andΔ1,Δ2,andΔ3being the corresponding pairing intensities.Here,n denotes theelectron concentration.Using the adjustable parametersΔ1,Δ2,andΔ3,we f ind the follow ing optimal f itting functions for the three electron concentrations:Thus,the pairing gap functions for ne=9.7 and ne=9.6 have a dom inantd-wavesuperconducting pairing along thenearestneighbor sites,which can also been seen from the sign and nodesof the gap functions shown in Figs.2(h)and 2(i).However,the gap function for ne=9.8 hasa dom inantd-wave superconducting pairing along the third-nearest-neighbor sites,so additional gap nodes appear in comparison with those for ne=9.7 and ne=9.6.

Fig.2.Static susceptibilitiesand superconducting gap functions fordifferentelectron concentrations:(a),(d),(g)n e=9.8,(b),(e),(h)n e=9.7,and(c),(f),(i)n e=9.6.The up panelshows the j eff=1/2 pseudospin susceptibilities Szz(blue),Sxx(green),Syy(red),-Sxy(magenta),and the largesteigenvalue of χdef ined in Eq.(3)(black)along theΓ–M–K–Γpath.M iddle panel:the distribution of the sum of the pseudospin susceptibility∑ηSηη(q)in the f irst Brillouin zone.Panels(g),(h),and(i)are the pairing functions for n e=9.8,n e=9.7,and n e=9.6,respectively.
Next,we turn to theelectron doped systems.In Fig.3,we show the pseudospin susceptibility S(q)and superconducting gap function for ne=10.1.From Fig.3(a),we can f ind that the peaksof the susceptibility are also located near M and its symmetric points.However,the intensities of the peaks are much larger than those for the hole-doped systems shown in Figs.2(d)–2(f),whichmightbe the origin of the persistence of the charge gap in the electron-doped systems found in the experiment,[44]i.e.,the strong pseudospin f luctuationshinder themovements of the doped electrons.The superconducting gap function in Fig.3(b)also shows a d-wave symmetry and theoptimal f itting function isgiven by We f ind that the electron pairing is dom inated by both the nearest-neighbor and next-nearest-neighbor parings,and they havenearly the same intensity.


Fig.3.(a)Static susceptibility and(b)superconducting gap function forelectron doped system with n e=10.1.
Thus,we f ind that the d-wave pairing mediated by the jeff=1/2 pseudospin f luctuations is themost favorable superconducting pairing symmetry for both hole and electron dopings.The explicit forms of the d-wave gap functionswe obtained here are expected to be helpful for identifying the pairing symmetry if superconductivity inα-RuCl3is realized experimentally in the future.
4.Conclusion
In summary,based on the multi-band Hubbard model with all t2gorbitals and by use of the random-phase approximation,we have investigated various particle–hole excitationsand possiblesuperconducting pairing symmetry in doped α-RuCl3,in which the strong spin–orbit coupling and electron correlations cause an effective total angularmomentum jeff=1/2 Mott insulator.We f ind that the jeff=1/2 pseudospin f luctuation dominatesoverother f luctuations in a large doping range,which suggests that the jeff=1/2 picture is still robustin the doped systems.Through projecting particle–particle interaction onto Fermi surfaces,we f ind that the dwave pairing is themost favorable superconducting pairing symmetry in both the hole-and electron-doped systems.
Appendix A:Decom position of particle–hole operator
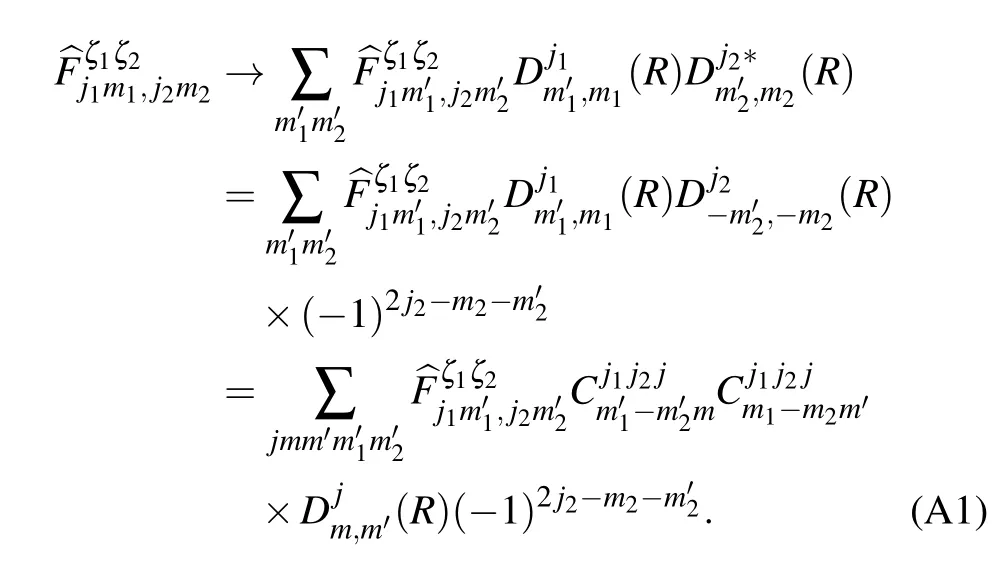
Here,Cj1j2jm1-m2m′are the Clebsch–Gordan coeff icients andDj1m′1,m1(R)is the representation of the group element R in SU(2).Thus,an irreducible representation of SU(2)isw ritten as

where N(jm)isanormalized factor.The tensoroperatorssatisfy the relation.For example,the explicit formalism ofis given by

Here,theoperators di,jmare setby aunitary transformation

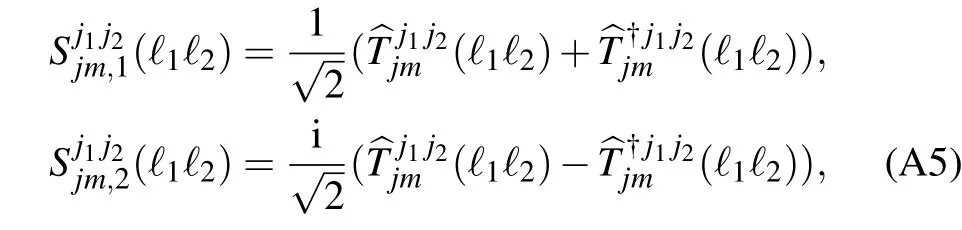
Then,itisconvenient to introduce theHermitian operatorsdef ined as with m≤0.Especially,for m=0 and?1=?2,the operator=is real.Under condition j=1,?1=?2,and j1=j2,theHermitian operatorsarespin operatorssuch as Sα?1(α=x,y,z).With these operators,the susceptibilityχ(q)is divided into 144×144 channelswhich include AB sublattice f luctuationsand the differentangularmomentum j f luctuations.
- Chinese Physics B的其它文章
- Computational study of inverse ferrite spinels
- Effectsof chem icalpressure on dilutedmagnetic sem iconductor(Ba,K)(Zn,M n)2As2*
- Surface stabilized cubic phaseof CsPb I3 and CsPbBr3 atroom tem perature*
- Raman scattering study ofmagnetic layered M PS3 crystals(M=M n,Fe,Ni)*
- Low tem perature Pmmm and C2/m phases in Sr2CuO3+δ high temperature superconductor*
- Crystallographic andmagnetic propertiesof van derWaals layered FePS3 crystal*

