基于R語言的兩配對樣本的均值差檢驗

常桂松 孫艷蕊 王洪曾

【摘要】? 兩總體均值差的檢驗是假設檢驗中的一個重要問題，常用在比較兩個處理方法的差異的分析中，當兩組樣本不是獨立時，不能利用獨立樣本的T檢驗。主要討論兩配對樣本的均值差的T檢驗，介紹了兩配對樣本的均值差的T檢驗的統計理論，并結合R語言介紹了其在實踐中的具體應用。

【關鍵詞】? R語言 T檢驗 配對樣本

假設檢驗是統計推斷的一個基本問題，實際生活工作中的很多問題利用統計方法分析，得到統計結論，進而有效地指導決策。利用兩總體均值差的假設檢驗，比較兩種處理方法的差異。當兩樣本X1，X2，L，Xn與Y1，Y2，L，Ym相互獨立時，可以利用獨立樣本的均值差的T檢驗。當樣本中測量到的兩組數據是同一對象在不同條件下測試的結果時，不能視為兩獨立的樣本，往往要對樣本進行配對處理，再利用單樣本均值差是否為零的T檢驗。如比較兩種安眠藥的安眠效果是否有差異，若試驗是在分為對照組和實驗組時進行的，此時兩組樣本是相互獨立的。若試驗是對一組試驗對象在不同時間下進行的，此時兩組樣本就不是相互獨立的，就不能利用獨立樣本的均值檢驗。再如要討論高三學生最后一次模擬考試的數學成績與高考真實的數學成績有無顯著差異？是否最后一次模擬考試的數學成績高于高考真實的數學成績？抽樣得到的兩組數據就不能視為兩個獨立樣本，需要對樣本數據進行配對后才能應用假設檢驗的理論進行分析。

一、理論及應用

1.檢驗的理論

由于配對樣本的各觀測具有對應關系，因此可將兩個樣本以觀測為依據對應做差（得到的樣本稱為差值樣本）。利用單樣本T檢驗法檢驗差值樣本的均值與零是否有顯著差異，進而得到兩總體均值是否有差異。

2. 檢驗的實例

R語言是目前應用最廣泛的統計軟件，由于R語言的開源性及其與一些軟件具有良好的兼容性，越來越多的數據分析工作首選R語言作為分析數據的工具。另外，在這個被很多專家和學者命名的大數據時代，許多科技工者每天置身于數據的汪洋大海和崇山峻嶺之中，高效利用R語言開展數據分析工作，毫無疑問會為科學研究做出高效的貢獻，并為工作奠定良好的基礎。目前，我國處于改革開放的轉型時期，面臨國際化的各個方面的激烈競爭，以高效的數據分析作為科學研究的手段，是促進國家科學發展，是國家在復雜多變的國際環境競爭中處于有利位置的重要戰略決策。利用R語言分析數據除了調用軟件內置的一些統計函數之外，用戶還可以自定義函數實現數據的統計分析。

可以從R的官方網站www.r-project.org免費下載并安裝R軟件，R主頁列出了R有關的各類信息，用戶下載R時，需要首先用鼠標點擊CRAN鏈接，選擇一個鏡像鏈接地址即可完成下載。成功下載R軟件后，即可按照Windows軟件的一般安裝方式進行安裝。

啟動R軟件后，用戶可以在R工作空間創建和管理R對像，調用R軟件中已加載包中的任何函數。在R語言中，兩配對樣本的均值差的檢驗對應的統計函數為t.test，格式為t.test（數值型向量名1，數值型向量名2，paired=TRUE，alternative=檢驗方向）

在統計函數t.test的參數調用中，數值型向量名1和數值型向量名2分別表示配對樣本觀測值的向量對應的名稱;參數paired=TRUE，表明觀測樣本為配對樣本，若paired=FALSE，則表示不對兩觀測樣本時行配對;參數alternative表明對立假設的檢驗方向，雙側檢驗時，對應的alternative=“two.side”，單側檢驗時，根據實際問題的背景，對應的對立假設的檢驗方向alternative=“less”或alternative=“greater”。

高考的數學成績對每一位考生非常重要，通過分析最后一次模擬考試的數學成績與高考真實的數學成績的數據，對學生的高考真實成績做出合理地指導。

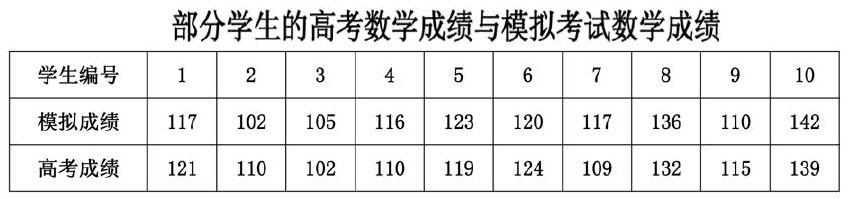
假設討論某中學的學生最后一次模擬考試的數學成績與高考真實的數學成績的問題中，隨機抽取一部分學生最后一次模擬考試的數學成績與高考真實的數學成績。如下表所示。

檢驗最后一次模擬考試的數學成績與高考真實的數學成績是否有差異？

調用R語言的函數t.test（a，b，paired=TRUE，alternative=“two.sided”），這里a表示學生最后一次模擬模擬考試的數學成績對應的數值型向量，b表示學生高考中真實的數學成績對應的數值型向量，輸出結果如圖所示

由輸出結果中可以看出，差值樣本對應總體的均值的置信水平為95%的置信區間是（-3.18977，4.5897），這個區間包含0.另外，檢驗的p-值是0.6934，比較 大，所以認為樣本沒有提供不利于原假設成立的顯著性證據，因而不能拒絕原假設，即認為最后一次模擬考試的數學成績與高考真實的數學成績無顯著差異。

二、總結

在比較兩總體均值是否有差異的檢驗中，一定要確定兩樣本是否獨立，不同情形對應著不同的統計方法，大多數數據分析工作者，很難區分兩樣本是否獨立。當兩組樣本是在不同的試驗對象中觀測得到的，可認為兩樣本是獨立的，可利用獨立樣本的均值差的T檢驗。當兩組樣本不獨立時，樣本值是同一組試驗對象在不同方法下的觀測值，常作配對處理，利用兩配對樣本的T檢驗，檢驗差值樣本對應的總體均值與零是否有差異。

本文研究了R語言在兩配對樣本的均值差的T檢驗中的應用。首先，簡要介紹了配對樣本，接著介紹了配對樣本的檢驗理論，最后接著介紹了R語言中配對板本的均值差的T檢驗的調用函數，并以具體實例討論R語言在實際問題中的應用。

參考文獻：

[1] 鄭明，陳子毅，汪嘉岡.數理統計講義[M].復旦大學出版社，2005.

[2]湯銀才.R語言與統計分析[M].高等教育出版社，2008.

[3]薛毅，陳麗萍.統計建模與R軟件[M].清華大學出版社，2007.