機器學習在綜合管廊規劃中的應用
□文/宋欣欣 閔海華 刁 鈺 秘 誠
綜合管廊作為目前城市現代化市政基礎設施的標志之一,其規劃路徑選擇至關重要,與用地功能及強度、道路等級及建成度、地下開發情況等多種因素有關[1],但現階段綜合管廊的規劃工作主觀性過強而科學性不足。
基于上述問題,引入機器學習方法,可以相對客觀地對某一地段管廊適建性進行評估;主要應用機器學習算法中的神經網絡算法以及梯度上升算法作為輔助管廊規劃工作的工具,神經網絡算法與梯度上升算法具有高度非線性的特點[2],可以描述管廊規劃工作中管廊的適建性與影響管廊建設各因素之間的關系。本文介紹了原始數據的獲取、神經網絡結構的建立、應用神經網絡工具進行管廊規劃三部分,展示了應用神經網絡算法的管廊規劃方法;在此基礎上引入了更為便捷簡單的梯度上升算法,與神經網絡算法進行對照分析。
1 研究方法
利用機器學習進行分析主要包括三部分:首先收集用于訓練的原始數據;然后選擇機器學習方法對原始數據中的訓練集進行學習;最后利用原始數據中的測試集對機器學習算法的準確度進行評估。利用這一方法可以減少決策問題中的主觀性[3]。
在管廊規劃問題中,機器學習具體方法:選取某管廊建設情況良好地區,對該地區街道的管廊適建性總體評分,同時對管廊建設的各分項影響因子打分,作為用于機器學習訓練的原始數據;構建學習模型,調整模型中的參數,以得到最適合管廊建設的機器學習模型;應用建立好的機器學習模型處理某一待規劃地區的影響因子得分,得到該地區每條道路的管廊適建性得分,根據這一得分完成管廊規劃工作。見表1和圖1。

表1 機器學習訓練原始數據
2 原始數據集獲取
如表1 所示,本研究認為與管廊適建性有關的因素共6 個,分別為用地功能及強度、管線重要度、道路等級及建成度、地下開發情況、交通路況和景觀功能。利用某地區290條道路的數據作為原始數據集進行訓練,原始數據集被劃分為兩部分,200 份作為訓練集,90份作為測試集。
3 基于神經網絡算法的適建性分析研究
首先利用基于神經網絡算法對輸入數據分析,求得影響因素與管廊適建性之間的關系,以定量解決管廊規劃問題。
3.1 算法概述
神經網絡(ANN)是20世紀80年代以來機器學習領域的一個研究熱點。近年來,人工神經網絡的研究工作取得了很大進展,成功地解決了現代計算機在模式識別、智能機器人、自動控制、預測估計、生物、醫學和經濟等領域中難以解決的許多實際問題。
人工神經網絡從信息處理的角度抽象人腦神經網絡,建立一個簡單的模型并根據不同的連接方法形成不同的網絡。神經網絡是一種操作模型,由大量的節點(或神經元)相互連接組成;每個節點表示一個特定的輸出函數,稱為激發函數(激活函數);每兩個節點之間的連接表示連接信號的加權值,稱為權值,相當于人工神經網絡的存儲器。網絡的輸出依賴網絡的連接方式、權重值和激勵功能,網絡本身是某種算法或函數的近似,也可能是一種邏輯策略的表達[4]。
3.2 算法數學原理
神經網絡結構由若干神經元組成,在深度學習技術中,通過損失函數的大小判斷一個神經網絡模型表現是否良好;而神經網絡隨著訓練性能逐漸提升的過程也在損失函數值下降的過程中體現。這個下降的過程指的就是通過梯度下降法找到損失函數中的全局最小值,當損失達到全局最小時該次訓練完成;該點得到的神經元權重值組成的神經網絡模型即為訓練好的神經網絡模型。
選用均方誤差MSE(Mean square error)作為損失函數。均方誤差損失函數是一種平方損失(Square loss),是反映估計量與被估計量之間差異程度的一種度量[3],是通過神經網絡得到的數據偏離真實值的距離的平方和的平均數,其表達式為
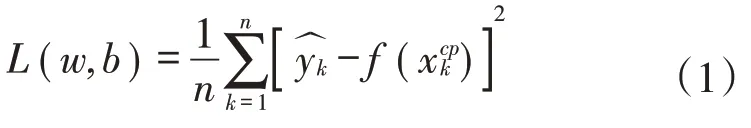
式中:k為當前計算損失函數的數據;n為總數據量為該組數據的期望值為輸入量通過神經網絡模型后的返回值,是關于神經網絡中每一個節點的權重值w的函數。
相較于其他損失函數,均方誤差損失函數較為適合用于回歸問題中對神經網絡模型表現進行評估。
神經網絡模型的調整是通過神經元間連接的權重值的調整實現的,相應地,損失函數值的下降過程同樣依托于權重值的更新。
3.3 算法實現
利用Matlab的神經網絡工具箱實現原始數據的讀取、神經網絡的搭建以及算法的評估等工作。見圖2。

圖2 Matlab設置人工神經網絡
首先進行原始數據的讀取:將原始數據分為包含因素的290組六維行向量,作為輸入數據;包含適建性結果的290組一維向量,作為目標數據。
在神經網絡算法中,原始數據被分為3部分:訓練集、測試集和確認集;其中確認集是為了確認訓練好的程序適用于各種不同的情況。在本案例中,將290 組原始數據中的70%作為訓練集,15%作為測試集,15%作為確認集。
原始數據讀取完成后開始神經網絡結構的搭建,本案例中神經網絡共有3層:第一層是輸入層,為六維向量,即與管廊適建性有關的6個因素;第二層是隱藏層,為神經網絡結構特有的算法結構,設置隱藏層的神經元共有10 個;第三層是輸出層,作為最終輸出結果的表達方式,為最終管廊適建性評估結果。見圖3。
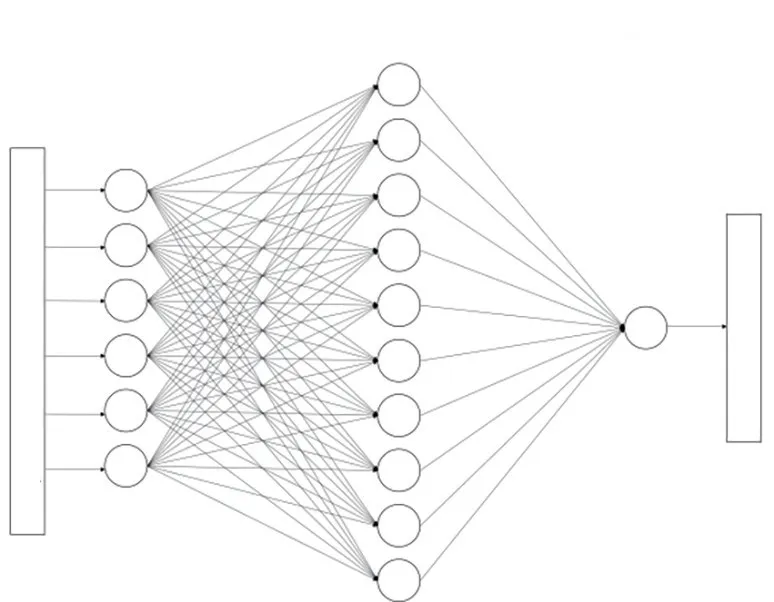
圖3 神經網絡結構
神經網絡結構建立好后,選擇萊文貝格-馬夸特方法作為訓練算法;設置好算法后,即可開始訓練得到結果。該方法能提供非線性最小化(局部最小)的數值解,能借由執行時修改參數達到結合高斯-牛頓算法以及梯度下降法優點的目的并對兩者之不足作改善(比如高斯-牛頓算法之反矩陣不存在或是初始值離局部極小值太遠)。
3.4 計算結果
結果顯示,神經網絡算法在進行到第296 次擬合時確認集表現最佳,其均方誤差達到最佳值。計算過程中梯度下降過程正常,其余各項指標的表現也在正常范圍內。計算結果的誤差很小,可以采用神經網絡方法計算得到的結果作為管廊規劃的依據。見圖4-圖6。
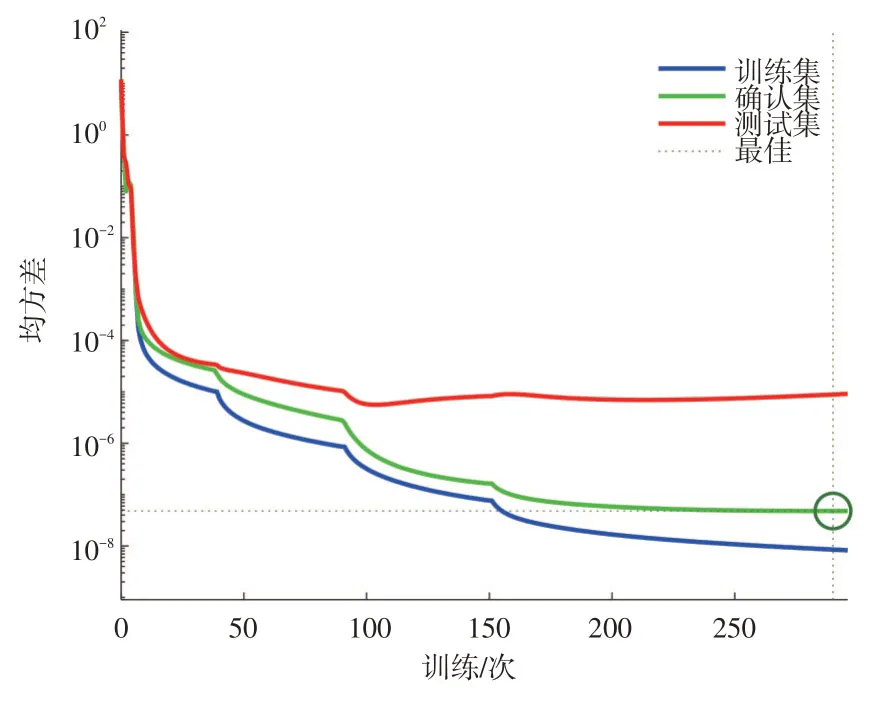
圖4 均方差情況
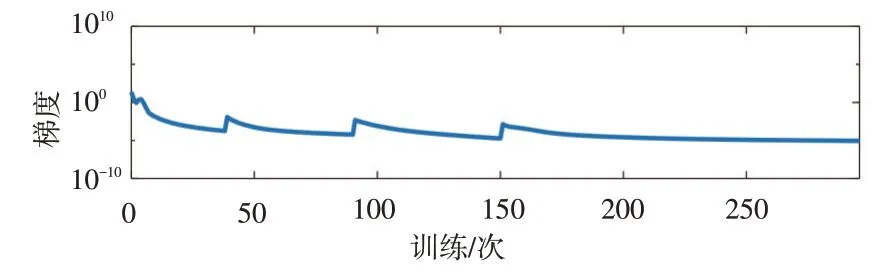
圖5 神經網絡計算過程中梯度變化
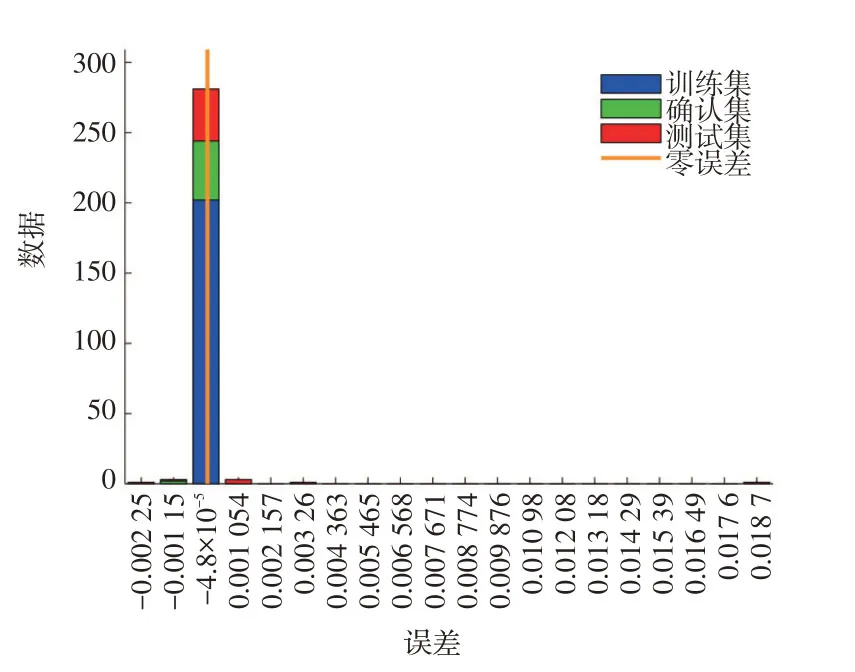
圖6 神經網絡計算結果誤差分布
4 基于梯度上升算法的適建性分析方法研究
神經網絡算法雖然能夠較好地解決非線性規劃問題,但其在實際操作過程中計算量較大、耗時長且對各項參數設置有較高要求,因此本研究進一步提出更為便捷簡單的基于梯度上升算法的管廊規劃。
4.1 算法概述
梯度上升算法為回歸問題中的一種算法。其本質是在給定已知數據的前提下對輸出量與輸入量間的關系算出一個一般性的估值函數,然后對給定新數據的輸出量進行估算;其目標是在已知數據框架內,使估算值與實際值的總均方誤差盡量更小;其實現是通過迭代的方法得到局部最大值[5]。
4.2 算法數學原理
通過迭代的方法逐步逼近函數最大值,以尋找最佳擬合參數,其迭代公式為

應用式(2)找到全局最大值,求得此時的參數,即為一個訓練過程,經過若干訓練過程后得到的結果即可用于管廊規劃。
4.3 算法實現
本算法通過python 語言實現,利用sklearn 庫中的Gradient BoostingRegressor 工具作為實現梯度上升的主程序并通過Numpy 庫中的reshape 工具將結果輸出為列向量,便于結果的導出和整理。見圖7。

圖7 導入梯度上升主程序
4.4 計算結果
將最終輸出結果導入Excel中進行分析,該算法在90個測試集中的表現見圖8。
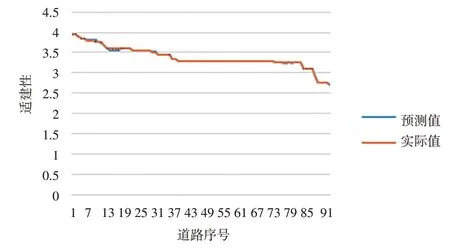
圖8 性誤差對照
由圖8可知,該算法表現良好,可以較為準確地實現管廊適建性的預測。
5 結論
1)利用神經網絡算法獲取影響因素與適建性關系,建立了良好的神經網絡模型并調整參數,使其在管廊規劃問題中有較好的表現。
2)提出了基于梯度上升算法的管廊規劃方法。該方法融合了神經網絡自動化、客觀性以及處理非線性關系的優點,同時避免了神經網絡發操作過程中計算量較大、耗時長的缺點。
6 建議
在確定影響因素與適建性關系的過程中共選用了兩種算法,經過對照分析,二者都可以準確地實現管廊適建性的預測,但均需要大量的數據庫用于訓練才可以有較為準確的表現。在本案例的290個數據的情況下這兩種算法已經取得了令人滿意的成績,若可以有更多數據作為原始數據供機器學習算法學習的話,其在管廊適建性預測上的表現則會更加優秀。此外,該項目實現過程中并未對機器學習算法實現過程中的各小參數進行調整,若嘗試調整算法中的各項參數,如:神經層層數,神經元數等,則可能會得到更為優秀的結果。

