不同巖性下TBM滾刀破巖過程離散元分析

楊開新，蔣明鏡,2,3,4,5，陳有亮，廖優斌

(1.上海理工大學 土木工程系,上海 200093；2.同濟大學 土木工程防災重點實驗室,上海 200092；3.同濟大學 巖土及地下工程教育部重點實驗室,上海 200092；4.同濟大學 地下建筑與工程系,上海 200092；5.天津大學 建筑工程學院,天津 300072)

1 研究背景

我國地勢西高東低，呈階梯狀分布，山巒疊嶂的西部發展需要建設大批穿越復雜地質構造帶的隧道工程。TBM在隧道開挖過程中不可避免地會遇到復雜巖層，而TBM刀盤上的滾刀受力不均容易導致傾覆、滾刀偏磨、刀圈斷裂與開裂等一系列施工問題。為了使滾刀破巖過程在災害最小和效率最高下進行，常常需要根據不同的地質條件不斷調整滾刀斷面參數及運行參數，而要實現這一過程，對于復雜巖層即不同巖性下滾刀破巖機理的研究就變得尤為重要。

Evans等[1]提出了盤形滾刀與巖石的相互作用理論。Nishimatsu[2]初步分析了滾刀破巖產生碎塊的過程。Yang等[3]采用一點二角度模型推導出三維復合巖層破巖理論解，系統地分析了貫入深度、滾刀轉速、巖層各向異性及上軟下硬復合巖層傾斜度對破巖過程中滾刀法向力、破碎方式、破碎區域大小的影響。通過對滾刀受力的預測以及巖渣的形成進行理論解析，可以初步從宏觀上認識滾刀破巖機理，但卻不能有效地對破巖過程中內部微觀信息的發展作出描述。

離散單元法[4](Discrete element method，DEM)因其能夠很好地模擬巖層破裂及大變形問題并能從微觀角度揭示其破壞機制，成為了滾刀破巖機理研究常用有效的方法。Gong等[5-7]建立了雙把TBM刀具侵入花崗巖的離散元模型,分析了節理間距與節理傾角對破巖過程的影響。Huang等[8]分析了滾刀侵入巖層過程，發現臨界貫入深度與特征長度有關。Jiang等[9]采用PFC2D模擬了完整和節理巖層的雙滾刀破巖過程，分析了不同節理傾角、間距下的最優刀距，并從微觀角度解釋其機理。另外，譚青等[10-14 ]采用PFC2D系統地模擬了TBM滾刀破巖過程。研究了球齒形、盤形滾刀的破巖機理并且較為全面地分析了破巖中的影響因素。孫亞[15]將基于微觀膠結試驗得到的巖石微觀力學模型[16-17]植入PFC軟件，通過陳賀[18]所做試驗得到的無厚度膠結強度包絡面標定了Lac du Bonnet花崗巖，模擬了單滾刀侵入單一完整巖層、雙滾刀侵入簡單節理巖層的破巖過程，較為系統地研究了不同影響因素對滾刀破巖效率的影響。蔣明鏡等[19]模擬了滾刀破巖過程并且重點分析了滾刀破巖的各階段的宏微觀機理。然而實際工程中，TBM滾刀常遇到復雜巖層，對于不同巖性差異下滾刀破巖機理的研究，不僅為復雜巖性下的滾刀破巖機理的研究提供了指導價值，更是復合巖層下滾刀破巖的研究基礎。為此本文采用離散單元法，于PFC2D商業軟件中植入考慮膠結尺寸的微觀接觸模型[16-17]，該模型能夠考慮巖石顆粒之間的膠結尺寸對強度包絡線的影響，更加符合巖體材料的真實破壞特性。通過研究不同巖性與滾刀刃數對于破巖效率的影響，力圖揭示其宏微觀機制，分析其內在破巖機理。

2 模型介紹

本文對巖石宏觀參數進行選定時，通過對不同巖性的單軸抗壓強度之間設置一定的梯度差，來標定具有一定代表性的巖性[20],本文選用的軟硬巖如表1所示。

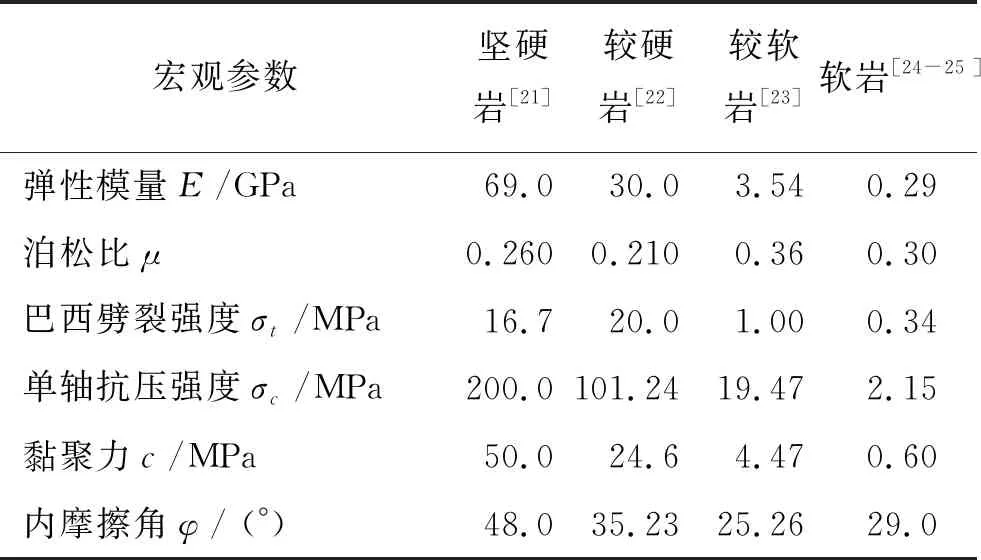
表1 本文數值模擬所需的巖石宏觀參數

對本文的巖石微觀接觸模型參數進行標定，標定的具體步驟如下：(1)先采用分層欠壓法[26]成樣，通過分層欠壓法能夠制備相對均勻的試樣，其中單軸壓縮試樣和雙軸壓縮試樣都采用寬高比為1∶2的長方形試樣，包含10 000顆粒；而巴西劈裂試樣采用正方形試樣，包含20 000萬顆粒。其中采用能夠較為準確合理地反映巖石類材料的顆粒級配[18]，如圖1示。該級配共有15種粒徑，最大粒徑是2.0 mm，最小粒徑是0.5 mm，平均粒徑是1.3 mm，不均勻系數是2.4，曲率系數是1.1。(2)對試樣進行預壓形成初始地應力。(3)加模型參數形成巖石試樣。(4)將巖石試樣切削成可加載的試樣。(5)加載試樣得到相應的力學指標。通過對單軸壓縮試樣進行加載得到單軸抗壓強度、彈性模量和泊松比；通過對巴西劈裂試樣進行加載得到巴西劈裂的峰值強度，換算得到單軸抗拉強度值。通過對雙軸壓縮試樣進行加載得到不同圍壓條件下的峰值抗壓強度，并計算得到內摩擦角和黏聚力。經過不斷地調整模型微觀參數，直到離散元試樣的宏觀力學特性和試驗的宏觀力學特性目標值相匹配，并在誤差許可范圍內。經細心的選取，最終標定的微觀參數如表2所示。

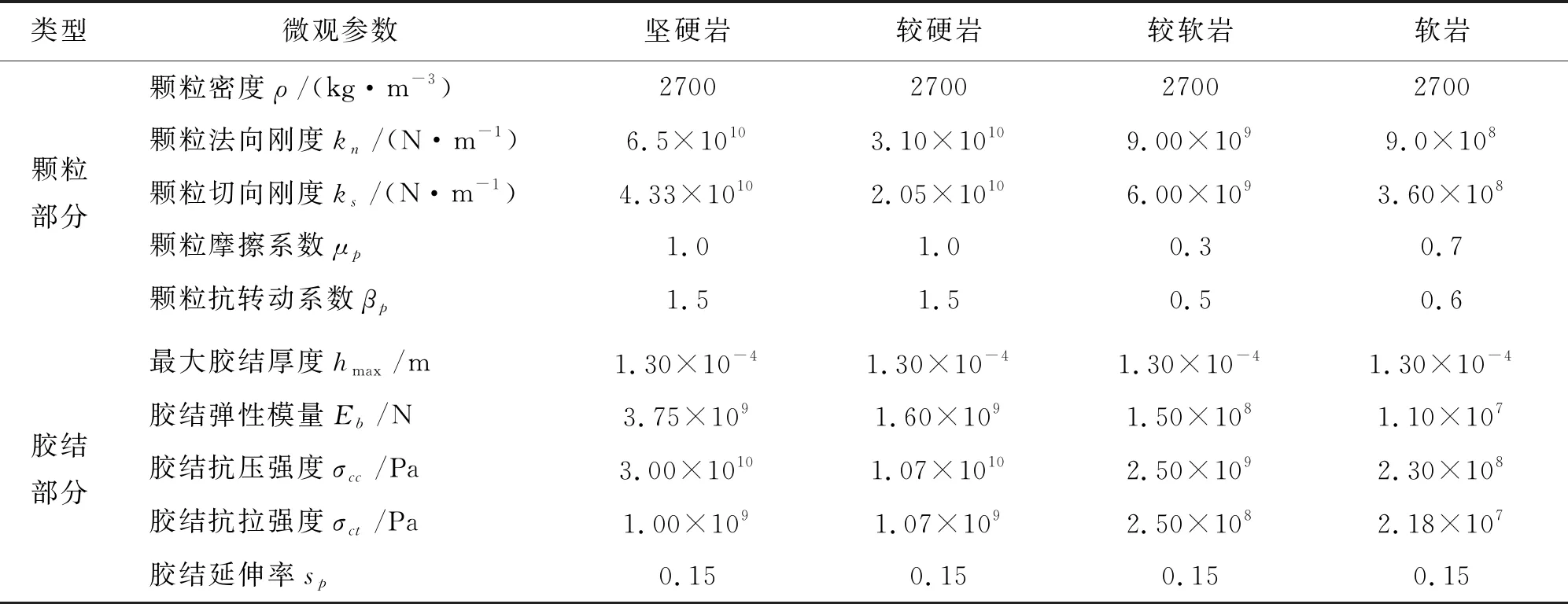
表2 DEM模擬的巖樣微觀參數

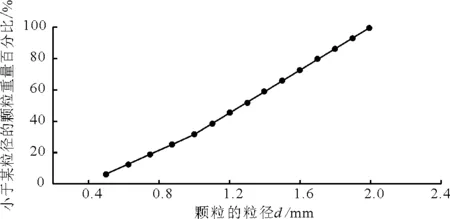
圖1 DEM巖石試樣的顆粒級配曲線[18]

3 滾刀破巖數值模擬

3.1 刀具及破巖模型

刀具消耗費用與換刀所消耗的時間是實際工程施工不可忽視的因素，而安裝在刀盤上的滾刀是TBM的關鍵部件和易損部件。如圖2所示，取單個滾刀受力分析可得到由刀盤推力提供的法向力、由刀盤扭矩提供的滾動力及刀盤旋轉產生的切向力，一般認為，在掘進過程中法向推力是破巖的主要因素，而滾動力的影響很小[27]，因此本文模擬了二維的滾刀侵入巖層的過程。刀盤上滾刀設計參數主要有滾刀間距S、貫入深度D、滾刀刃角α、滾刀刃寬w，采用施工中運用比較廣泛的常截面盤形滾刀，模擬中滾刀刃寬w=15 mm、刃角α=60°、滾刀間距S=100 mm固定不變，重點研究滾刀數目和不同巖性對破巖的影響。模擬的滾刀采用PFC5.0軟件中的墻命令生成，單個滾刀采用六面獨立的墻體閉合圍成，整個破巖過程中認為是剛性的，墻體的法向剛度和切向剛度比顆粒剛度略大即可，顆粒與墻之間的摩擦系數取為零。

本文研究了研究4種巖性下單滾刀、雙滾刀、三滾刀的破巖機理，以較硬巖為例，破巖示意圖如圖3所示。根據袁聚云等[28]的研究，當滾刀刃寬與巖石試樣寬度的比值小于0.02時，可以有效地減少滾刀破巖過程中的尺寸效應。因此本文選取的試樣尺寸為760 mm×380 mm，顆粒數目約30×104，試樣孔隙比為0.2。

3.2 破巖阻力與侵深關系分析

本文模擬了4種巖性下不同滾刀刃數的破巖過程，其中選取較硬巖作為對照組，探究不同巖性與滾刀刃數下的破巖機理。推力-侵深曲線是滾刀侵入巖層的基本關系曲線，如圖4所示。根據推力-侵深曲線特征可以將不同刃數下的滾刀破巖過程分為3個階段：加載階段、卸載階段和殘余躍進階段。加載階段滾刀推力基本隨著侵入深度呈現線性增加，直至推力峰值；卸載階段達到峰值階段，滾刀推力會迅速跌落至較小的值，這對應于滾刀前方巖層破碎，滾刀受到的阻力瞬間減小，刀頭會出現短暫的臨空現象，甚至有可能產生刀頭瞬間脫落的危害；殘余躍進階段，破巖阻力隨著滾刀的侵入深度波動，這是由巖層破碎引起的殘余躍進，這種波動常常伴隨一個穩定值，此時對應的膠結破壞點增幅減小趨于穩定，說明了滾刀行進的阻力在不斷減小，并且此時巖層內部裂紋很難產生，試樣已經破壞。此外，隨著滾刀刃數的增加，多滾刀的推力-侵深曲線與單個滾刀作用的曲線一致性較好。從不同刀刃數的膠結破壞數分析看，本文的膠結破壞主要分為兩種，拉剪破壞和壓剪破壞。在加載階段產生的膠結破壞數較小，裂縫開始形成；到了卸載階段，裂縫不斷發育、擴展，此時膠結破壞數增加較為明顯；而到了殘余躍進階段，裂縫已發育完全，巖石試樣已破壞，膠結破壞數達到穩定水平。綜上所述，膠結破壞數的發展與峰值推力變化階段是宏、微觀的相互對應，且拉剪破壞產生膠結破壞數發展規律與壓剪破壞的規律一致性較好。

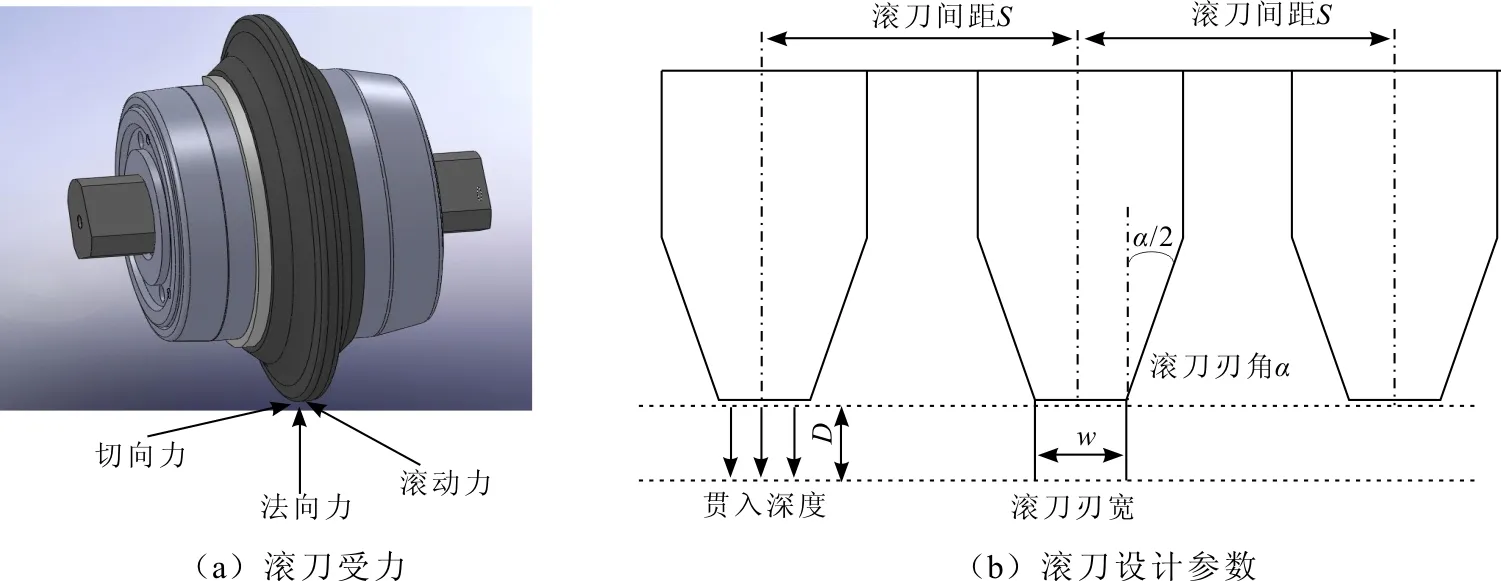
圖2 全斷面掘進機刀盤及滾刀示意圖

圖3 3種滾刀刃數下滾刀破巖模型圖(單位：mm)

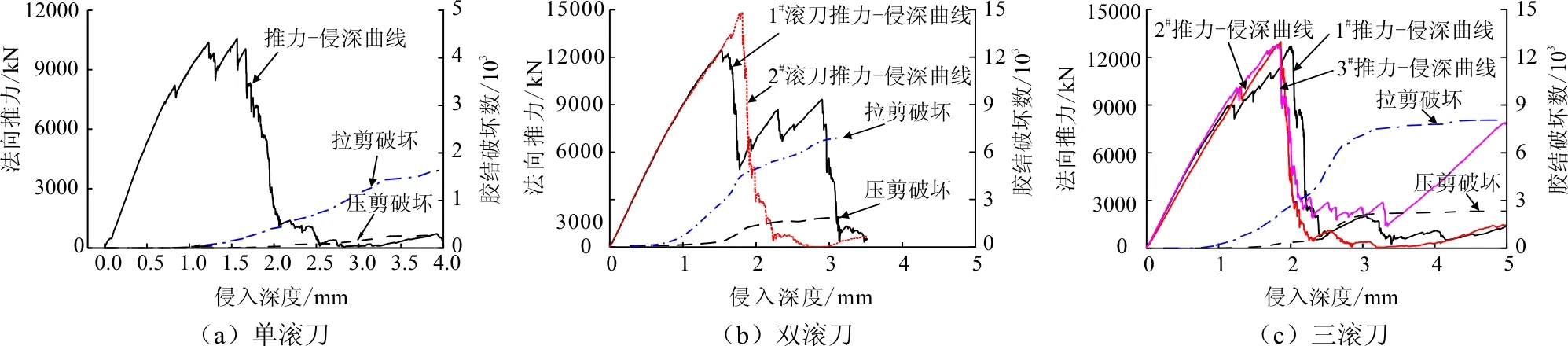
圖4 多刃滾刀破較硬巖層的推力-侵深關系曲線圖

3.3 裂紋擴展機理分析

圖5為較硬巖單滾刀、雙滾刀與三滾刀不同貫入度下的力鏈分布圖，圖5中的線條粗細表示接觸力的大小，接觸力越大，線條越粗，力鏈越密。由圖5可見，貫入度為1 mm時出現Sanio[29]所提及的靜水壓力核，部分力鏈與集中區域散射出的力鏈互相垂直呈現弧形分布，這與Moon等[30]所做實驗觀察到的現象一致。圖5(c)左下方出現局部區域力鏈阻斷，主要是因為崩碎的塊體與母體已經沒有接觸，故無法傳遞力，該貫入度下的應力水平很低，達到了殘余躍進狀態，此時破巖不需要太多的能量。圖5(e)雙滾刀作用下力鏈分布對稱，受力傳遞路徑比較清晰均勻。圖5(g)中左右兩把滾刀受力出現不均勻，主要是因為巖層產生了破碎區，這與單滾刀時的情況是一致的。由圖5(i)可知，三滾刀作用時力鏈分布廣而密，整個試樣主要受到壓應力，可以觀察到，此時較硬巖還是處于彈性階段，出現3個力鏈核，受力比較清晰；圖5(j)較硬巖力鏈發展沒有較大的變化，但單個滾刀作用下方接觸力鏈更為濃密；對于圖5(k)，滾刀下方剛剛出現巖層破碎區域，接觸力鏈呈現了不對稱分布的特征，表現為右側大而左側小的核狀，主要是因為左側滾刀下方巖層破碎區域大，導致了左側滾刀出現了滾刀臨空區域，而右側的滾刀則還處于受力集中區域。

圖5 較硬巖單滾刀、雙滾刀與三滾刀不同貫入度下力鏈分布圖

選取了不同滾刀刃數與巖性下的破巖宏觀局部圖，如圖6所示。其中圖6(a)～6(d)為單滾刀、圖6(e)～6(h)為雙滾刀、圖6(i)～6(l)為三滾刀情況下4種巖性的破巖局部示意圖。

由圖6(a)～6(d)可知巖層的破壞模式主要可以分為兩大類：塊狀剝落類和碎渣剝落類。其中堅硬巖、較硬巖和較軟巖巖層可以明顯看出滾刀左右側有較大的巖塊已剝落，而軟巖則出現眾多微小裂縫，表面碎渣剝離母體，伴隨著飛濺的巖渣。觀察圖6(e)～6(h)，發現4種巖性的巖層都出現了雙滾刀之間的貫通裂隙，越硬的巖層的破巖容易停留在表層，形成表裂縫和斜裂縫；中等巖性的巖層易形成較長的貫通裂縫；而軟巖則易形成呈表面的崩碎狀、容易發展的縱向裂縫和中裂縫。通過圖6(i)～6(l)可知，三滾刀的破巖模式主要分兩種類型：破碎區貫通型和破碎區非貫通型。堅硬巖或軟巖都較容易形成破碎區貫通，堅硬巖呈現塊狀貫通脫落而軟巖出現顆粒崩碎狀貫通。對于介于之間的巖石則更傾向形成破碎區非貫通，主要是因為中間巖性的巖層既沒有堅硬巖由于高強度形成的完整性使得裂縫相互貫通，也無法像軟巖一樣形成表層的小裂隙實現貫通，只能形成一定體積的破碎，而這些破碎的巖渣在未達到相互貫通之前已經與自由面貫通而形成塊體剝落。

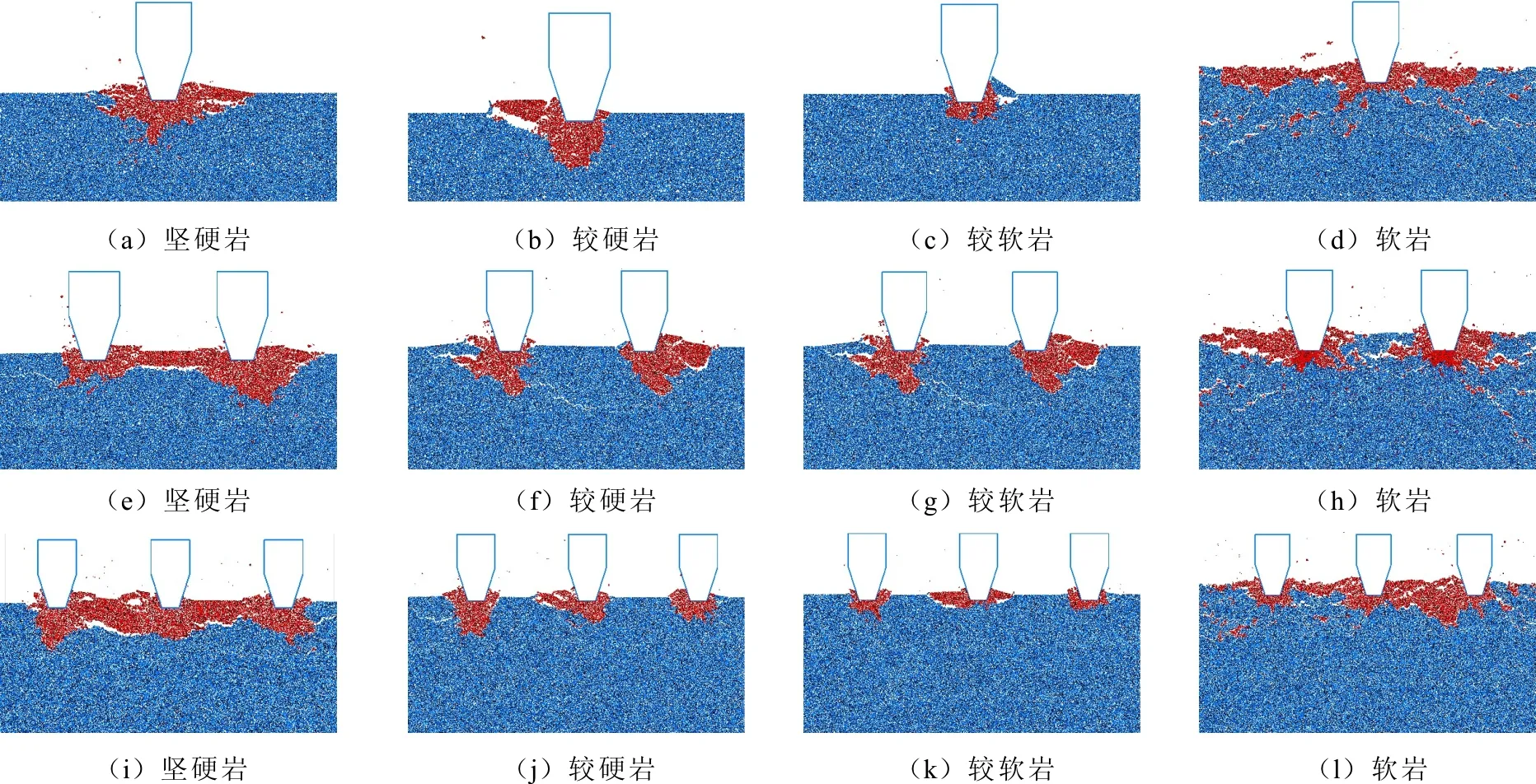
圖6 不同滾刀刃數下不同硬度巖層破巖局部示意圖

3.4 結果討論與分析

圖7(a)為不同滾刀刃數的破巖過程中的膠結破壞數目。膠結破壞總數從微觀角度上描述了破巖能力，膠結破壞數目越大，表明滾刀的破巖能力越強。對于堅硬巖和較硬巖可知，膠結破壞數目隨著滾刀刃數的增加而增加，表明破此類硬巖，通過增加滾刀刃數能夠有效提高破巖能力。但對于較軟巖而言，從單滾刀升到雙滾刀破巖能力是升高了，但從雙滾刀升到三滾刀破巖能力沒增加反而減小了，這可能是因為低強度的巖層由于兩側滾刀的側壓力施加給中間滾刀正下方的巖層形成了一定的束桶作用，導致中間巖層強度在一定程度得到了提高。另外，Jiang等[9]采用了膠結破壞比能耗作為評價破巖效率的一個重要指標，這是對傳統室內試驗定義滾刀破巖效率的“比能”的一個重要補充。其中膠結破壞比能耗的定義為：破巖過程中滾刀所消耗的能量和滾刀作用下產生的膠結破壞點總數的比值。膠結破壞比能耗從微觀的角度解釋了由于單個膠結破壞產生微小裂隙所消耗的能量，這能夠在一定程度上表征破巖過程中破巖效率，并且膠結破壞比能耗越低，破巖效率越高。

圖7(b)給出了不同巖性下3類滾刀破巖時膠結破壞比能耗變化規律。其中滾刀破巖所消耗的能量通過荷載-侵深曲線積分得到，而膠結破壞總數都統一取了貫入度為5mm時膠結破壞點的總數的穩定值。由圖7(b)可知，對于堅硬巖采用三滾刀時破巖效率最高，對于較硬巖、較軟巖和軟巖則采用單滾刀時破巖效率最高。

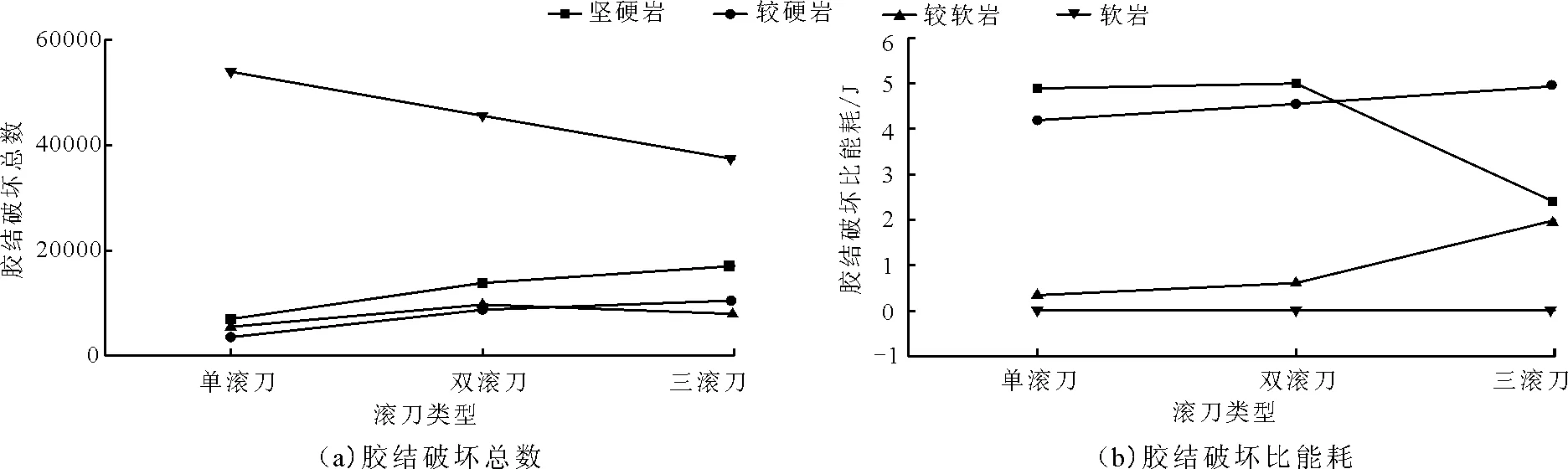
圖7 不同巖層下三類滾刀破巖膠結破壞分析

圖8峰值法向推力 圖9比能耗與巖石單軸抗壓強度關系曲線

圖8為三類滾刀破巖時滾刀所受到的峰值法向推力。在破較軟巖與軟巖時，3類滾刀的峰值法向推力差異較小；而對于堅硬巖與較硬巖時，雙滾刀與三滾刀會出現左右滾刀峰值法向推力相差較大，主要是因為破巖進入峰值階段不一致，導致破巖過程中常常會出現一側滾刀正下方巖層先破碎，而另外一側滾刀達到峰值前就已經因為巖層出現破碎而導致推力跌落。這正是離散元模擬滾刀破巖的一大優勢，能夠很自然地模擬破巖過程中的漸近破壞。另外，對于3類滾刀，巖性的差異對峰值法向推力的影響是巨大的，這與工程實踐明顯是一致的。

根據譚青等[31]采用的不同巖性的巖石滾刀切削試驗，試驗中的巖石為花崗巖、板巖、砂巖、石灰華與混凝土，其中對應了堅硬巖、較硬巖、較軟巖和軟巖。通過試驗中單滾刀切割干燥巖石所得破巖比能耗數據，建立單滾刀破巖比能耗與巖石單軸抗壓強度的關系曲線，與本文單滾刀情況下不同巖性的膠結破壞比能耗對比，如圖9所示。在巖石單軸抗壓強度小于100 MPa時，破巖比能耗隨著單軸抗壓強度增加而增加，這與膠結破壞比能耗的趨勢一致性較好，說明在較低巖石單軸抗壓強度下，膠結破壞比能耗是可以作為評價破巖效率的一個指標。但當強度超過100 MPa時，試驗中出現較大跌落，這與模擬區別明顯。主要是因為不是所有的微觀裂隙都能發展成破巖所需要的宏觀裂縫，有些微小裂隙還可能出現閉合現象，沒有形成主裂紋的膠結破壞在破巖過程的貢獻是微小的，只是在一定程度上削弱了巖層。舉例來說，做功不變時，當破巖過程中有大塊的巖渣掉落時，所需要的膠結破壞數目可能不需要很多，但在工程上此時破巖效率是較高的，而微觀上膠結破壞數目越少，破巖效率越低，這與圖9中軸壓超過100 MPa時曲線走勢是一致的，這說明了采用膠結破壞比能耗盡管在一定程度上能夠描述破巖效率，但還是存在缺陷。

4 結 論

本文通過離散單元法，采用基于室內試驗提取的考慮膠結尺寸的巖石微觀膠結接觸模型，模擬了不同滾刀刃數下侵入4種單一巖性巖石的過程。主要研究結果表明：

(1)通過模擬單滾刀、雙滾刀及三滾刀侵入4種不同巖性巖石的破巖過程，發現不同刃數的滾刀破巖過程均可以分為3個階段：加載階段、卸載階段及殘余躍進階段。

(2)膠結破壞類型主要分為兩種：拉剪破壞和壓剪破壞。對于堅硬巖和較硬巖，膠結破壞數目隨著滾刀刃數的增加而增加，但對于較軟巖和軟巖而言，增加滾刀刃數并不能增加膠結破壞數目。

(3)破巖過程中滾刀受到的阻力可以用峰值法向推力表示，阻力與巖性密切相關，巖石單軸抗壓強度越大，破巖時的阻力也越大。

(4)采用膠結破巖比能耗來評價破巖效率，其中對于堅硬巖，三滾刀的破巖效率最高，而對于較硬巖、較軟巖和軟巖，采用單滾刀破巖效率更高。