基于PSO-MUSIC算法的分布式目標DOA估計

李 海， 居夢琪， 張 喆

(中國民航大學天津市智能信號與圖像處理重點實驗室， 天津 300300)

0 引言

機載雷達具有探測距離遠、覆蓋范圍大且具有較強的機動性和靈活性等優點，因此，在軍事和民用領域應用越來越廣泛[1]。相控陣體制雷達的收發天線陣列緊密排布，各陣元發射相關信號，在空間同向疊加，可以獲得較高的天線增益[2]。為了使目標波達方向(Direction of Arrival，DOA)的估計不模糊，通常要求陣列陣元間距滿足空間采樣定理，即陣元間距小于等于波長的一半[3]。當要求天線陣列具有很高的角度分辨率時，就需要較大的陣列孔徑，此時，傳統陣列需要的陣元個數較多，而在空間欠采樣情況下，可大大減少所需陣元數，不僅減少了系統成本而且削弱了天線間的互耦效應[4]。但空間欠采樣會使天線方向圖出現柵瓣或高旁瓣問題，影響角度估計性能。所以研究空間欠采樣下的DOA估計技術就顯得十分重要[3]。

經典的DOA估計算法都以點目標信號源為模型來簡化算法，降低分析的復雜性[5]。然而，由于復雜環境下的散射、反射、衍射及折射等原因導致大量的多徑現象，從而造成信號源在空間發生一定的角度擴展[6]，這類發生角度擴展的信號源統稱為分布式信號源[7]。因此，當信號源的空間分布特性不能忽略時，點信號源模型往往不能準確描述陣列觀測數據，那么用點源為模型的DOA估計方法的性能會惡化，甚至得不到正確的估計結果[7-8]。

目前，分布式目標的DOA估計方法有MUSIC算法[9]、TLS-ESPRIT算法[10]和最大似然算法[11]等，但以上算法均是在陣列滿足空間采樣定理下實現的。針對空間欠采樣的情況，本文提出了一種基于PSO-MUSIC算法的分布式目標波達方向估計方法。該方法首先建立分布式目標信號模型，然后利用粒子群優化算法優化天線陣元間距，改善空間欠采樣情況下天線方向圖的柵瓣和高旁瓣問題，最后利用分布式目標導向矢量結合MUSIC算法得到目標信號功率譜，從而估計空間欠采樣下分布式目標的中心波達方向。

1 信號模型

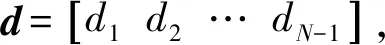
圖1 任意線陣陣列示意圖

分布式目標為一群滿足一定統計分布特性的散射體的集合[6]。那么分布式目標回波即為波束范圍內所有散射點回波的疊加。考慮遠場空間有一個分布式目標信號源入射到N元線陣上，陣列觀測信號數據x表示為

(1)

式中：n表示噪聲；Q,αi分別表示分布式目標中的散射粒子總數和第i個散射粒子的幅度；θ表示分布式目標的中心DOA；θi表示第i個散射粒子與中心DOA的角度偏差，為隨機變量，滿足一定的概率分布，如高斯分布、均勻分布、三角分布等；b(θ+θi)表示分布式目標第i個散射粒子的導向矢量，且

b(θ+θi)=a(θ)⊙g(θi)

(2)

式中，⊙表示Hadamard積，a(θ)表示分布式目標中心DOA方向上的導向矢量，g(θi)表示具有確定性角密度函數(高斯分布、均勻分布、三角分布等)的分布式目標在中心DOA上的擴展。本文采用角密度函數為高斯分布的分布式目標，Δ為擴展角度，則a(θ)和g(θi)可表示為

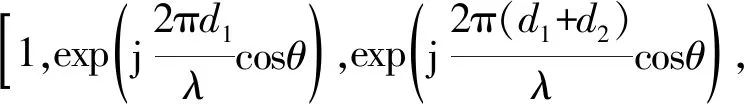
(3)

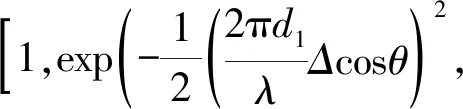
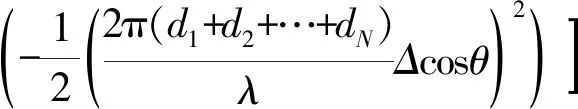
(4)

2 分布式目標中心DOA估計方法

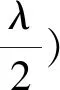
2.1 粒子群優化算法優化陣元間距

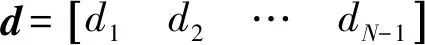
PSO算法是根據適應度函數來評價粒子位置“好壞”程度的，那么適應度函數的選取很關鍵。本文的優化問題為尋找天線方向圖高旁瓣電平最小情況下的陣元間距，因此適應度函數可設為

(5)

式中，

k=1,2,…,Z

(6)

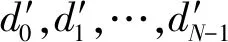
(7)

式中，φw為天線方向圖的主旁瓣分界角度。

本文將尋找天線方向圖高旁瓣電平最小時的陣列陣元間距轉化為在粒子群優化算法搜索使得適應度函數最小的粒子位置。以第k個粒子為例，在第r次迭代中適應度函數有如下關系：

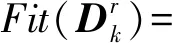
k=1,2,…,Z

(8)

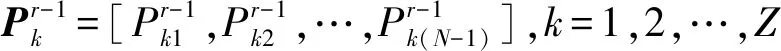
(9)

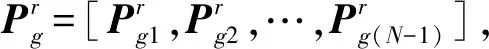
(10)

當前后兩次迭代的適應度函數值小于門限值時滿足迭代終止條件，得到的全局極值Pg即為PSO算法優化后的陣列陣元間距。

粒子每次迭代更新速度和位置都是與個體極值和全局極值相關的，更新規則如下：

(11)

(12)

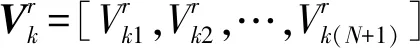
(13)

式中，a表示當前迭代次數，T表示總的迭代次數，即為迭代終止條件滿足時的次數。

2.2 估計分布式目標中心DOA

根據PSO算法優化后的陣元間距得到相應的陣列流形，在該陣列流形下接收數據，并得到其協方差矩陣表示如下：

R=E[xxH]=Rs+Rn

(14)

由于信號與噪聲相互獨立，接收數據協方差矩陣可分解為信號、噪聲相關的兩部分。其中Rs為分布式目標的協方差矩陣，Rs為噪聲協方差矩陣。對協方差矩陣R進行特征分解有

(15)

式中，(·)H表示共軛轉置，Us表示由大特征值對應的特征矢量張成的子空間即信號子空間，Un表示小特征值張成的子空間即噪聲子空間。在理想情況下，信號子空間與噪聲子空間正交，即

(16)

其中，分布式目標信號角密度函數已知，且能夠通過式(2)得到廣義的分布式目標導向矢量b(ψ)。利用式(16)的特點，可得到MUSIC算法的譜估計公式為

(17)

那么本文中所求分布式目標中心DOA的代價函數如下：

(18)

3 算法流程

PSO-MUSIC算法主要步驟如下：

1) 在給定范圍內隨機初始化總群中所有粒子的位置和速度；

2) 計算每個粒子的適應度函數值；

3) 每個粒子所得到的適應度函數值與上一次迭代選擇出的個體極值的適應度函數值比較，如果較好，則替換當前個體極值；

4) 每個粒子所得到的適應度函數值與整個總群中選擇出的全局極值的適應度函數值比較，如果較好，則替換當前全局極值；

5) 根據式(11)、式(12)更新粒子速度和位置；

6) 如果滿足終止條件，則輸出最優位置，否則返回步驟2)繼續運行直到滿足終止條件為止；

7) 由PSO優化后的陣列接收數據并得到數據協方差矩陣，對協方差矩陣進行特征分解，確定信號子空間和噪聲子空間，根據信號子空間與噪聲子空間的正交性構造有關DOA的代價函數；

8) 最后通過尋找代價函數的最小值得到分布式目標的中心DOA估計結果。

4 仿真結果及分析

4.1 分布式目標仿真

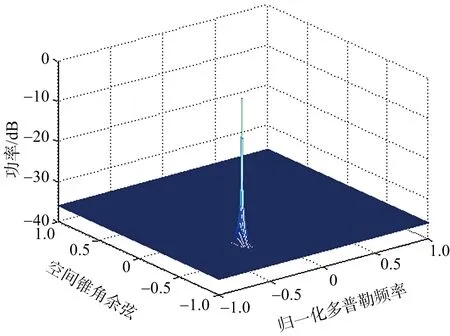
圖2 點目標模型

圖2為傳統的點源信號模型，圖3為本文采用的分布式目標信號模型，目標的中心DOA為60°，角度擴展為2°。從圖中可以看出，分布式目標在空間上會有一定的擴展，不再是一個單純的點源，因此其陣列觀測矢量也與點目標不同。

圖3 分布式目標模型

4.2 粒子群優化算法優化陣元間距

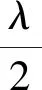
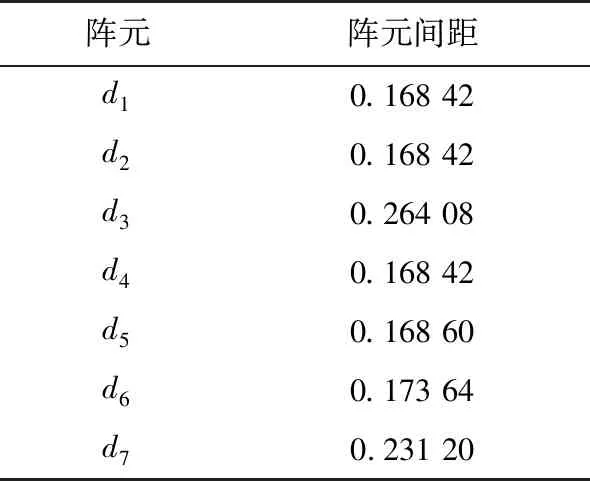
表1 PSO優化后陣元間距

空間欠采樣可以利用較少的陣元數得到更大的陣列孔徑，但是均勻欠采樣下天線方向圖會出現柵瓣，如圖4所示，非均勻欠采樣下天線方向圖的旁瓣電平較高，如圖5所示，不利于分布式目標的DOA估計。圖6為PSO算法優化的陣列天線方向圖，可以看出PSO算法優化后的陣列可以消除柵瓣，得到旁瓣電平較低情況下的天線方向圖，有利于提高目標的參數估計性能。圖7為粒子群優化算法的收斂曲線，即為PSO算法隨著迭代的進行適應度函數的變化情況，可以看出本文選取的迭代次數滿足終止條件。

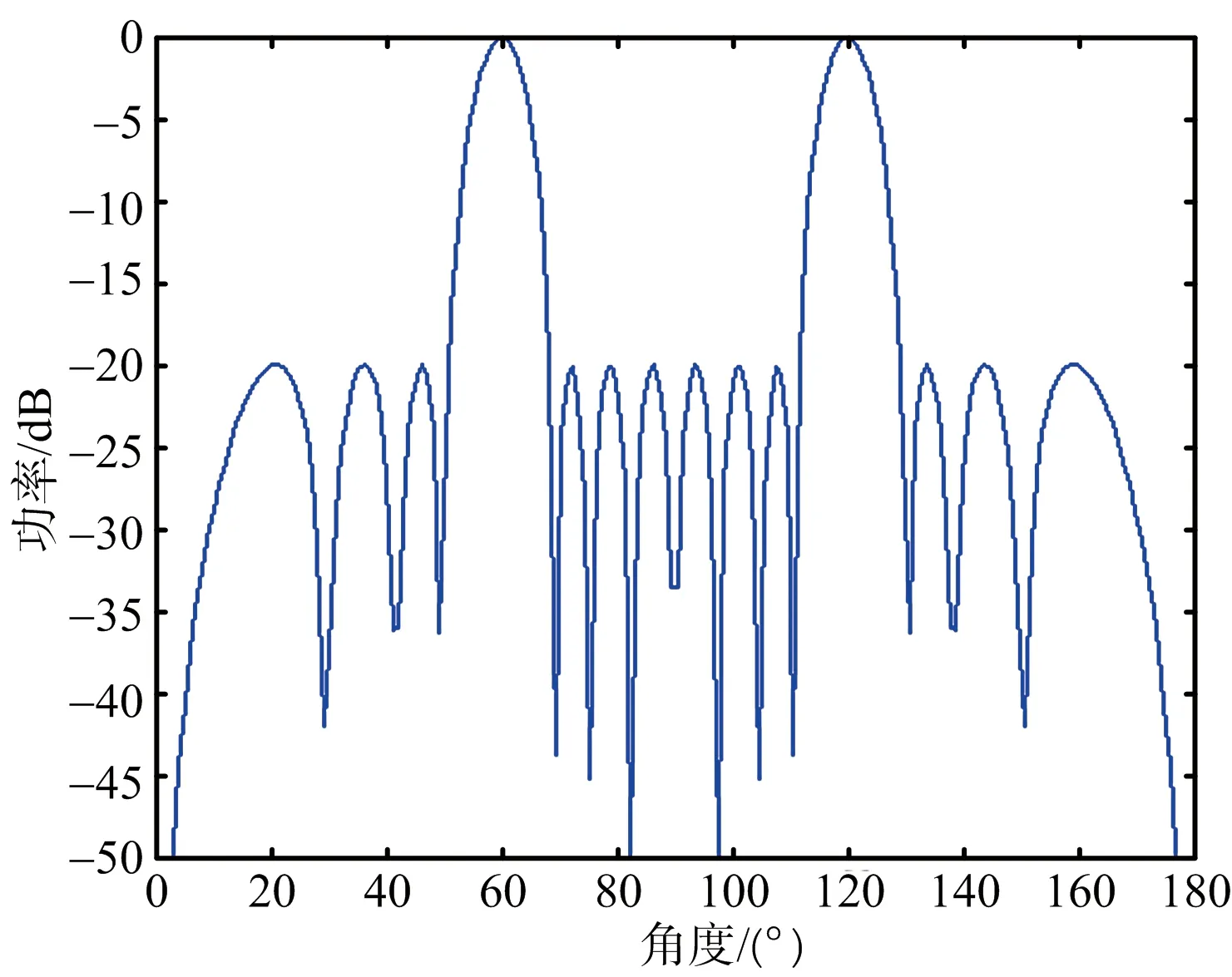
圖4 均勻稀疏陣天線方向圖

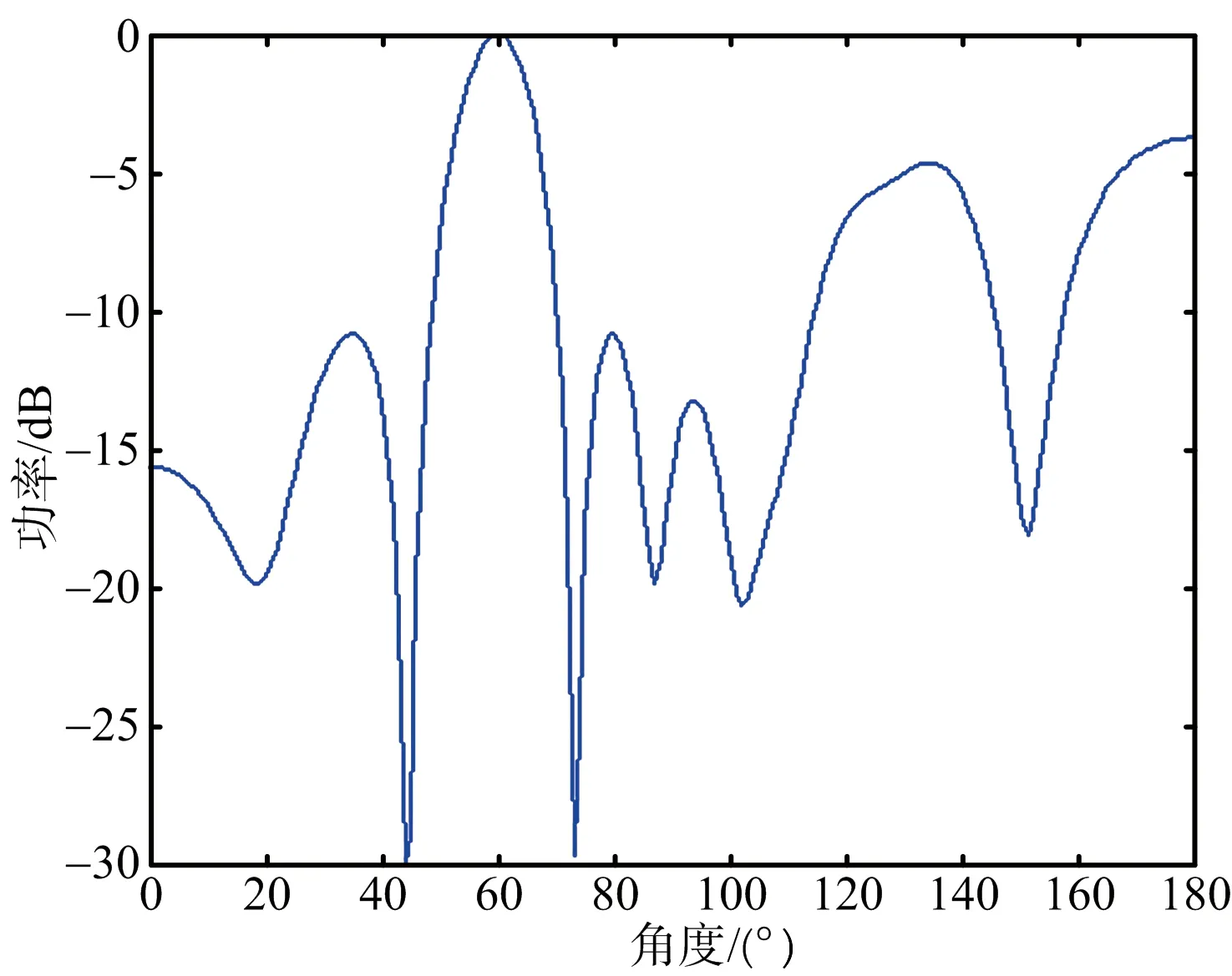
圖5 隨機非均勻陣天線方向圖

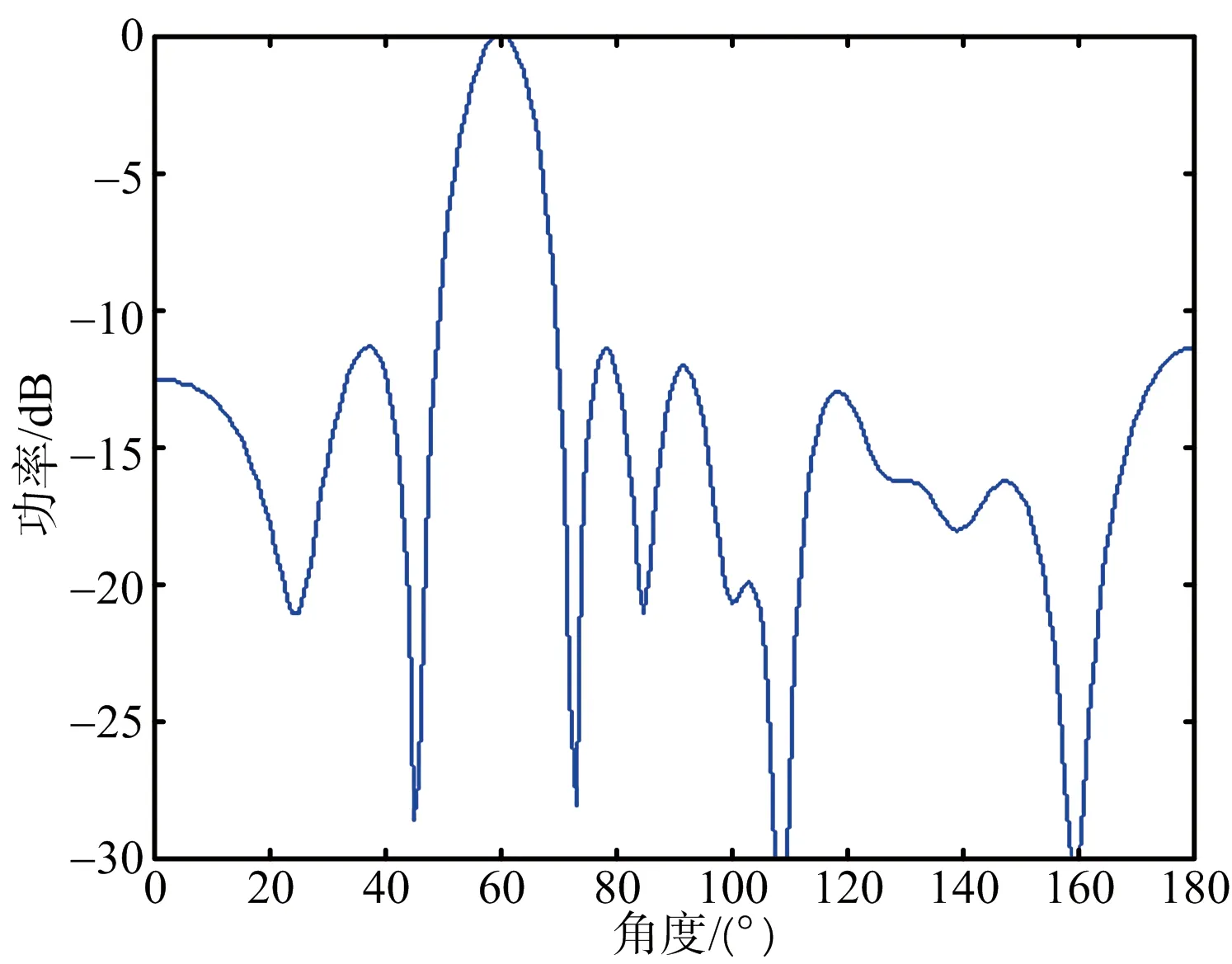
圖6 PSO算法天線方向圖

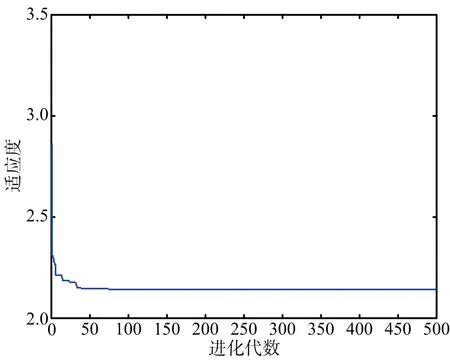
圖7 PSO算法收斂曲線

4.3 基于PSO-MUSIC算法的DOA估計

圖8為本文算法的分布式目標中心DOA估計結果圖，從圖中可以看出，PSO-MUSIC算法的DOA估計中沒有出現偽峰，可以得到較準確的分布式目標DOA估計結果。

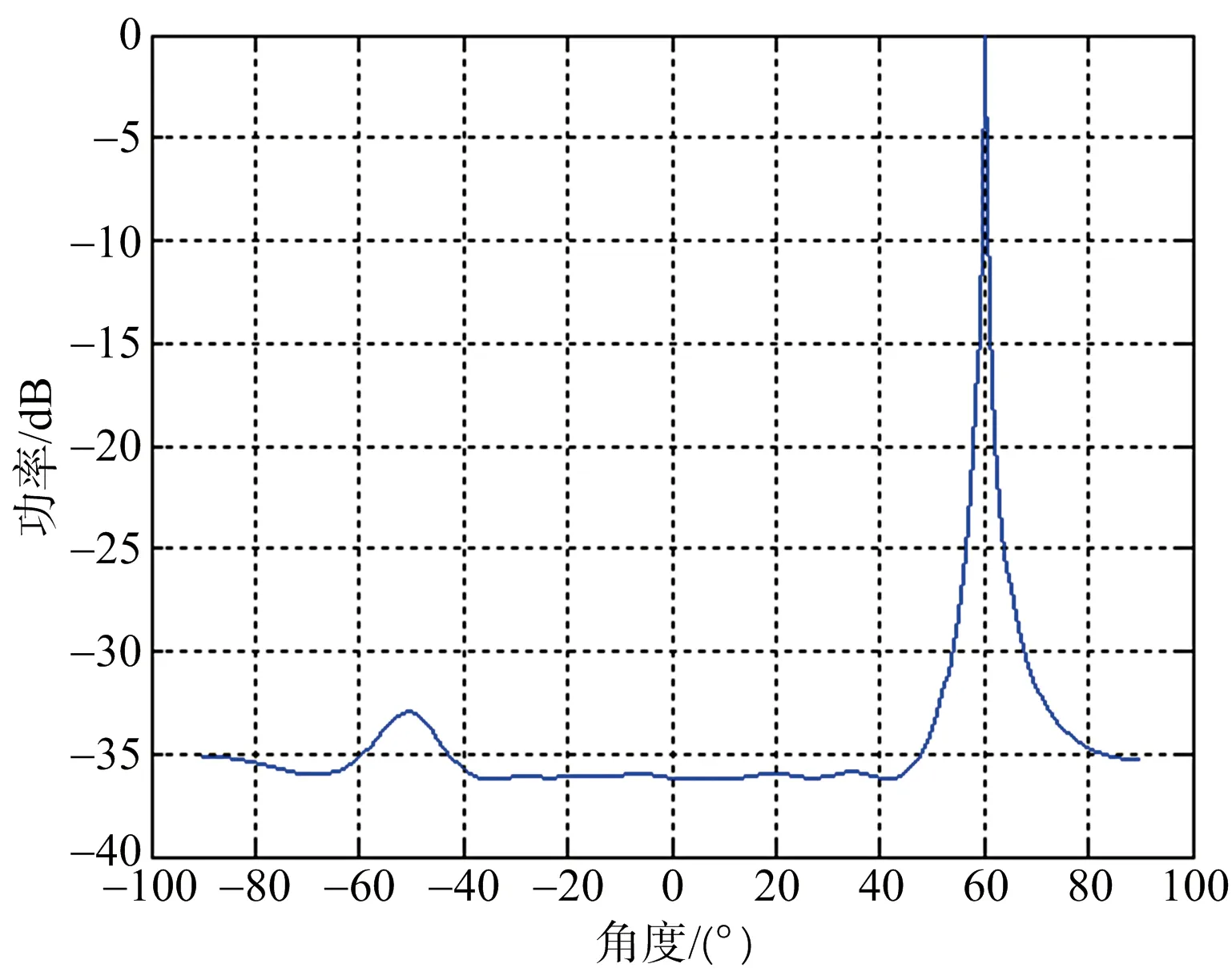
圖8 MUSIC算法DOA估計結果

5 結束語

針對空間欠采樣情況下目標DOA估計的多值問題，本文提出了一種基于PSO-MUSIC算法的分布式目標DOA估計方法。該方法首先利用粒子群優化算法優化陣元間距，得到天線方向圖高旁瓣電平最小情況下的陣元間距，然后利用該陣元間距得到陣列流形并接收回波數據，最后通過MUSIC算法得到陣列回波功率譜，并通過功率譜的最大值，能夠獲得空間欠采樣下分布式目標中心DOA的準確估計。仿真結果表明，在空間欠采樣情況下，本文方法能夠獲得準確的分布式目標中心DOA估計。